Слайд 2Понятие размерности
Интуитивно мы понимаем термин размерность как число координат, необходимых для задания положения точки

внутри фигуры. Так, любая линия (например, окружность или прямая) одномерна – достаточно всего одной координаты, чтобы точно указать точку, а плоскость и поверхность шара двумерны. Но в математике такое «определение» не всегда работает хорошо: его трудно применить к очень большому числу разнообразных фигур и множеств, в том числе и к фракталам. Поэтому фрактальную размерность определяют по-другому.
Слайд 3Допустим, что фигура F, размерность которой мы хотим найти, расположена на плоскости. А плоскость,

в свою очередь, покрыта сеткой из квадратиков со стороной . Через обозначим число квадратиков, которые пересекаются с фигурой F (объединение всех таких квадратиков содержит в себе F). Ясно, что это число зависит от размера квадратиков: чем они меньше, тем больше их нужно, чтобы покрыть фигуру. Если эта зависимость выражается степенным законом: число пропорционально некоторой степени , то будем считать, что фигура F имеет размерность D (вполне может случится, что число D не целое).
Слайд 4Размерность Минковского
Определение, данное на прошлом слайде, и является определением фрактальной размерности по

Минковскому. Для «хороших» фигур оно дает тот же результат, что и интуитивное представление о размерности.
В более общем случае размерность Минковского или грубая размерность ограниченного множества в метрическом пространстве равна
где – минимальное число множеств диаметра , которыми можно покрыть наше множество.
Слайд 5Если предел не существует, то можно рассматривать верхний и нижний предел и

говорить соответственно о верхней и нижней размерности Минковского.
Близким к размерности Минковского понятием является размерность Хаусдорфа. Во многих случаях эти размерности совпадают, хотя существуют множества для которых они различны.
Слайд 6Примеры
Размерность отрезка равна 1, так как необходимо отрезков длины , чтобы покрыть

отрезок длины a. Таким образом
Размерность квадрата равна 2, так как число квадратиков с диагональю , необходимых, чтобы покрыть квадрат со стороной a, ведет себя примерно как .
Размерность кривой Коха равна .
Слайд 7Свойства
Размерность Минковского конечного объединения множеств равна максимуму из их размерностей. В отличие

от размерности Хаусдорфа, это неверно для счётного объединения.
Нижняя размерность Минковского любого множества больше либо равна его размерности Хаусдорфа.
Размерность Минковского любого множества равна размерности Минковского его замыкания. Поэтому имеет смысл говорить лишь о размерностях Минковского замкнутых множеств.






 Масштаб аэрофотоснимков
Масштаб аэрофотоснимков Устройство и принцип работы дизельного двигателя
Устройство и принцип работы дизельного двигателя Плотность. Плотность мрамора
Плотность. Плотность мрамора Клепаные и сварные соединения
Клепаные и сварные соединения Квантовая физика. Фотоэффект
Квантовая физика. Фотоэффект Русские изобретения, которыми пользуется весь мир
Русские изобретения, которыми пользуется весь мир Деформация Сила упругости, закон Гука (Тема 1, Тема 2)
Деформация Сила упругости, закон Гука (Тема 1, Тема 2) Ветровой электрогенератор challenergy
Ветровой электрогенератор challenergy I-D диаграмма влажного воздуха
I-D диаграмма влажного воздуха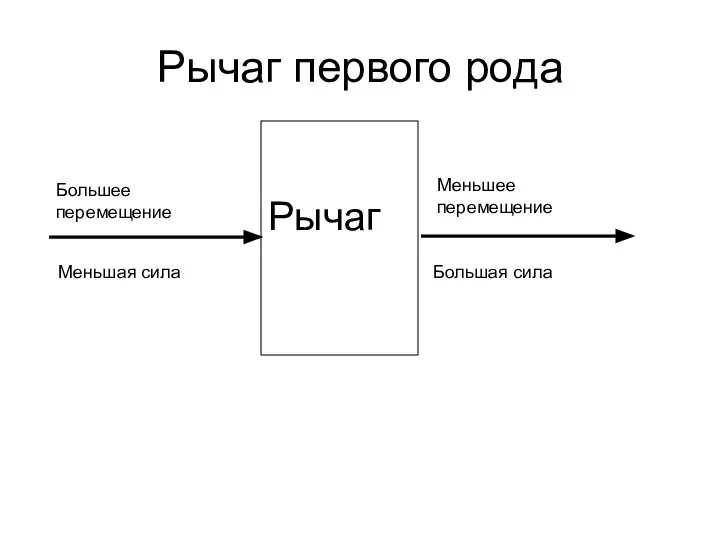 Рычаг первого рода
Рычаг первого рода Сопротивление материалов
Сопротивление материалов Тепловое расширение
Тепловое расширение А.В.Перышкин Физика, 8 класс. Решение задач
А.В.Перышкин Физика, 8 класс. Решение задач Теория и практика формообразования заготовок
Теория и практика формообразования заготовок Проверь себя!!!
Проверь себя!!! Первый пароход 4/2 класс
Первый пароход 4/2 класс Законы сохранения в механике. Лекция № 5
Законы сохранения в механике. Лекция № 5 Механика деформируемого твердого тела
Механика деформируемого твердого тела Давление твердых тел
Давление твердых тел Светофор. Внеклассное мероприятие по физике
Светофор. Внеклассное мероприятие по физике Понятие индукции
Понятие индукции Ядерный реактор
Ядерный реактор Электростатика
Электростатика Презентация на тему Давление света
Презентация на тему Давление света  Задачи на соединение проводников
Задачи на соединение проводников Презентация по физике "Скорость" -
Презентация по физике "Скорость" -  Относительность движения
Относительность движения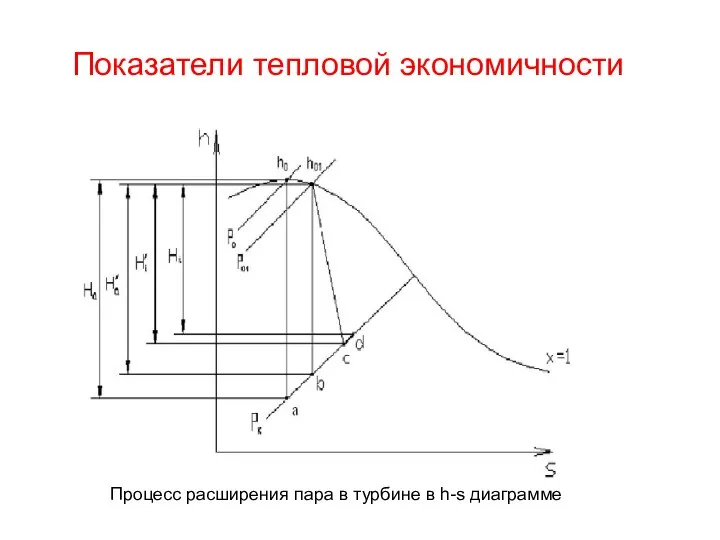 Показатели тепловой экономичности
Показатели тепловой экономичности