Содержание
- 2. Плоские системы сил Система сходящихся сил – силы такой системы лежат в одной плоскости, причем все
- 3. 2.2 Система трех сходящихся сил Главной задачей статики является составление уравнений равновесия для каждой из систем,
- 4. Еще проще уравнения можно записать в виде: F1х + F2х + F3х = 0; F1у +
- 6. Пример 2.1. Найти величины и направления действия уравновешивающих сил F2 и F3 графическим и аналитическим способами,
- 7. Решение графическим способом Принимаем масштаб сил: 1см-10кН. Из произвольной точки а откладываем в масштабе известную силу
- 8. 2. Составляем уравнение в форме (2.1): 3. Из первого уравнения получаем выражение для F2: 4. Подставляем
- 9. 2.3 Система четырех и более сходящихся сил При решении задач о равновесии четырех и более сходящихся
- 11. Скачать презентацию
Слайд 2Плоские системы сил
Система сходящихся сил – силы такой системы лежат в одной
Плоские системы сил
Система сходящихся сил – силы такой системы лежат в одной
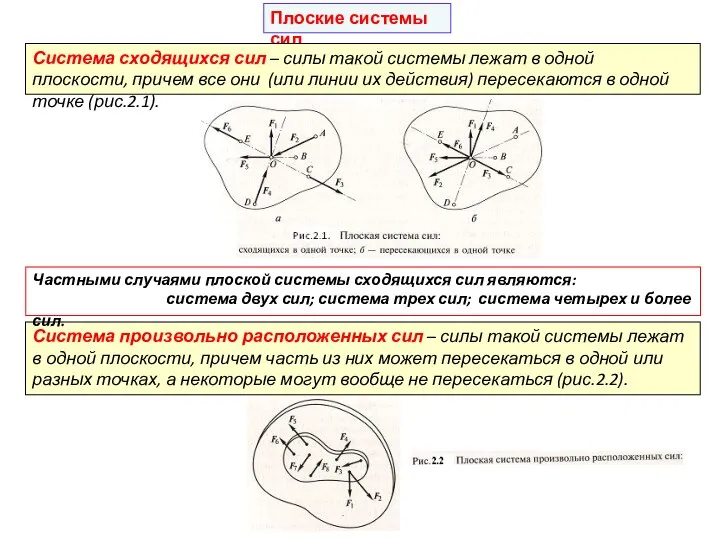
Система произвольно расположенных сил – силы такой системы лежат в одной плоскости, причем часть из них может пересекаться в одной или разных точках, а некоторые могут вообще не пересекаться (рис.2.2).
Частными случаями плоской системы сходящихся сил являются:
система двух сил; система трех сил; система четырех и более сил.
Слайд 32.2 Система трех сходящихся сил
Главной задачей статики является составление уравнений равновесия
2.2 Система трех сходящихся сил
Главной задачей статики является составление уравнений равновесия

В статике для любого из приведенных случаев могут быть решены следующие задачи:
-сложение или вычитание сил;
-нахождение условий равновесия сил.
Эти задачи могут быть решены двумя способами: графическим (использование графических действий над векторами) и аналитическим (использование способа проекций).
Система трех сил, под действием которых тело находится в равновесии, - это наиболее распространенный случай, встречающийся в практических задачах.
Общий порядок решения задач о равновесии трех сил аналитическим способом.
Суть аналитического способа состоит в том, что сумма проекций всех находящихся в равновесии сил на обе координатные оси Ох и Оу должна быть равна нулю.
∑Х=0; ∑Y=0
(2.1)
∑Х, ∑Y – алгебраическая сумма проекций сил на ось х и ось у.
Слайд 4Еще проще уравнения можно записать в виде:
F1х + F2х + F3х =
Еще проще уравнения можно записать в виде:
F1х + F2х + F3х =

(2.2)
где F1х, F2х, F3х - проекции сил F1, F2, F3 на ось Х, F1у, F2у, F3у -на ось Y.
Для решения задач аналитическим способом должны быть известны углы между силами и координатными осями.
Общий порядок решения задач о равновесии трех сил графическим способом.
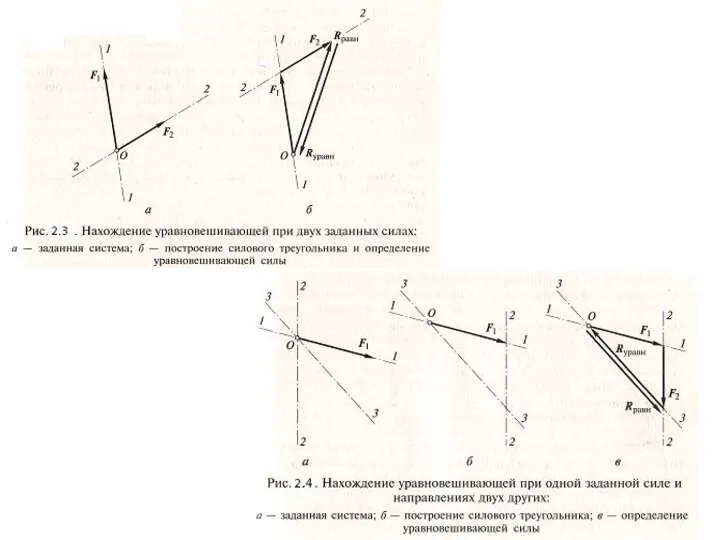
Устанавливают масштаб сил. Из произвольной точки на листе в принятом масштабе откладывают заданные две силы, или заданную силу и направления двух других. Строят силовой треугольник. Если заданы две силы, то третью – уравновешивающую можно найти, соединив конец вектора 2-й силы и начало вектора 1-й (рис.2.3,б). В начало вектора 1-й силы будет направлена стрелка вектора уравновешивающей силы. Если заданы одна сила и направления действия 2-й и 3-й силы, которые уравновешивают первую, то через начало и конец вектора 1-й силы проводят две параллельные заданным направлениям линии так, чтобы они пересеклись в одной точке и получился треугольник (рис.2,4б,в). Измеряют в масштабе сил каждый вновь полученный отрезок и находят величины сил. Ставят стрелки на полученных отрезках так, чтобы все они были направлены в одну сторону при обходе треугольника, т.е. конец вектора 3-й силы совпадал с началом вектора 1-й.
Слайд 6Пример 2.1. Найти величины и направления действия уравновешивающих сил F2 и F3
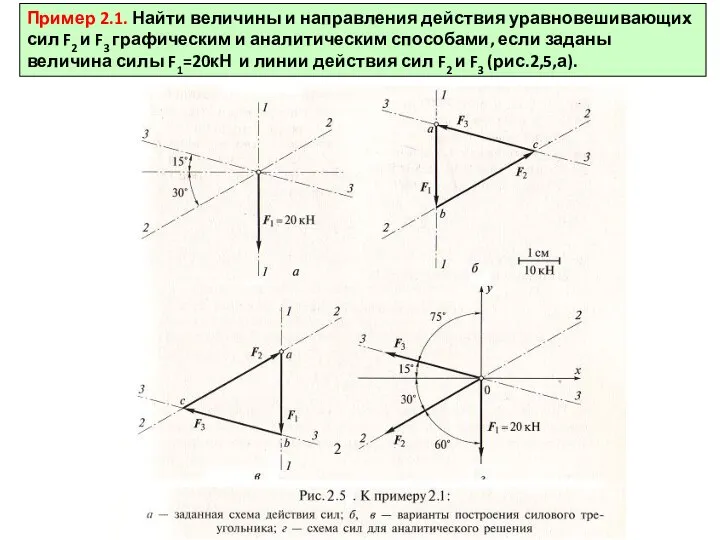
Пример 2.1. Найти величины и направления действия уравновешивающих сил F2 и F3
Слайд 7Решение графическим способом
Принимаем масштаб сил: 1см-10кН.
Из произвольной точки а откладываем в
Решение графическим способом
Принимаем масштаб сил: 1см-10кН.
Из произвольной точки а откладываем в

Через начало и конец вектора силы F1, т.е. через точки a и b, проводим линии, параллельные линиям действия сил F2 и F3 так, чтобы они пересеклись в одной точке с. При этом силы F2 и F3 могут оказаться как справа от силы F1 (рис.2.5,б), так и слева от нее (рис.2.5,в). Это не является ошибкой, но все же правильнее, когда при обходе треугольника номера сил идут в нарастающем порядке, т.е. вариант F1, F2, F3 предпочтительнее. Силы F2 и F3 являются уравновешивающими силу F1 .
Измеряем отрезки bc и ca (2,8см и 2,5см). Так как 1см соответствует 10кН, получаем F2 =28кН и F1 =25кН
Расставляем стрелки на отрезках bc и ca . Поскольку направление силы F1 задано (вниз), остальные силы должны быть направлены так, как показано на рис.2.5,б.в, при этом конец вектора силы F3 будет совпадать с началом вектора силы F1.
Решение аналитическим способом
1. Проводим оси координат Ох и Оу. Силы направляем из начала координат по заданным линиям действия 3-3 и 2-2. Направление выбираем произвольно (например, влево - рис.2.5,г). Проставляем углы между направлениями всех сил и координатными осями.
Слайд 82. Составляем уравнение в форме (2.1):
3. Из первого уравнения получаем выражение для
2. Составляем уравнение в форме (2.1):
3. Из первого уравнения получаем выражение для

4. Подставляем выражение для F2 во второе уравнение и находим F3 :
5. Определив F3 находим F2 :
F2 направлена в сторону, противоположную показанной на рис.2.5,г, о чем говорит знак «минус» . Направление силы F3 совпадает с ранее заданным на рис.2.5,г.
Вывод: сравнив ответы, можно сделать вывод о том, что аналитический способ более точный.
Слайд 92.3 Система четырех и более сходящихся сил
При решении задач о равновесии
2.3 Система четырех и более сходящихся сил
При решении задач о равновесии
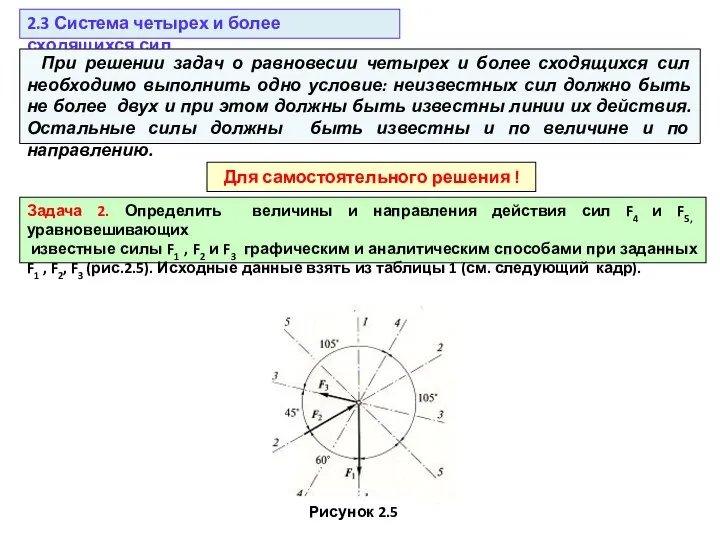
Для самостоятельного решения !
Задача 2. Определить величины и направления действия сил F4 и F5, уравновешивающих
известные силы F1 , F2 и F3 графическим и аналитическим способами при заданных F1 , F2, F3 (рис.2.5). Исходные данные взять из таблицы 1 (см. следующий кадр).
Рисунок 2.5
 Механика. Теория относительности А. Эйнштейна. Постулат постоянства скорости света
Механика. Теория относительности А. Эйнштейна. Постулат постоянства скорости света Задачи на массовую долю элемента
Задачи на массовую долю элемента Электрический заряд
Электрический заряд Активация в ядерной физике. (Тема 2.8)
Активация в ядерной физике. (Тема 2.8) Электроснабжение в многоэтажном доме
Электроснабжение в многоэтажном доме Силикаты. Физические свойства
Силикаты. Физические свойства ВКР: Оценка потенциала утилизации ВЭР за нагревательными печами
ВКР: Оценка потенциала утилизации ВЭР за нагревательными печами Классификация тепловых двигателей
Классификация тепловых двигателей Концепции современного естествознания
Концепции современного естествознания Светодиодное растениеводческое освещение
Светодиодное растениеводческое освещение Tesla
Tesla Свойства твёрдых тел, жидкостей и газов
Свойства твёрдых тел, жидкостей и газов Молекулярно-кинетическая теория
Молекулярно-кинетическая теория Измерение объёма взвешиванием
Измерение объёма взвешиванием Скорость. Единицы скорости
Скорость. Единицы скорости Взаимодействие цвета и вещества
Взаимодействие цвета и вещества Потенциальная и кинетическая энергия
Потенциальная и кинетическая энергия Порівняння роботи рухомого складу за різними видами тяги
Порівняння роботи рухомого складу за різними видами тяги Результаты экспериментальных исследований теплофизических характеристик автоклавного ячеистого бетона
Результаты экспериментальных исследований теплофизических характеристик автоклавного ячеистого бетона Магнитно-оптический контроль ферромагнитных и неферромагнитных объектов. Требования к средствам проверки VIN кода
Магнитно-оптический контроль ферромагнитных и неферромагнитных объектов. Требования к средствам проверки VIN кода Работа. Энергия. 8 класс
Работа. Энергия. 8 класс Презентация на тему Ядерные реакции
Презентация на тему Ядерные реакции  Электротехника и Электроника
Электротехника и Электроника Презентация на тему Постоянные магниты. Магнитное поле Земли
Презентация на тему Постоянные магниты. Магнитное поле Земли  Учитель начальных классов ГОУ СОШ №403 Шельпук Н.А.
Учитель начальных классов ГОУ СОШ №403 Шельпук Н.А. Метрология ионизирующих излучений. (Лекция 3)
Метрология ионизирующих излучений. (Лекция 3) Параметры потребителей и источника электроэнергии
Параметры потребителей и источника электроэнергии