Солитоны

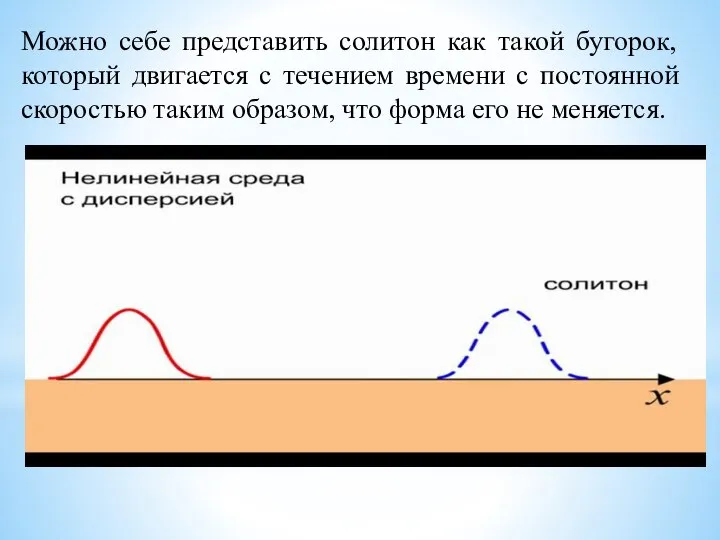
Можно себе представить солитон как такой бугорок, который двигается с течением времени с постоянной скоростью таким образом, что форма его не меняется.

Можно говорить также об обобщённых солитонах (breathers), −
« решение, которое дышит».
Они представляют собой такие бугорки, которые двигаются с постоянной средней скоростью, но при этом их форма меняется, осциллирует, “дышит”

Джон
Скотт
Расселл

Уравнение Кортевега — де Фриза
Солитон
ut− 6uux + uxxx = 0

Иоганнес Дидерик
Кортевега
Густав де Фриз

Нелинейное уравнение Шредингера
Обобщённый солитон

Вполне интегрируемые системы
Бесконечное число интегралов движения
Гарднер, Грин, Крускал, Миура,
Лакс,
Фаддеев и его школа,
Дринфелд, квантовые группы
Сато, Мива, Джимбо

Питер Дэвид Лакс

Фаддеев Людвиг Дмитриевич

Дринфельд Владимир Гершонович

Столкновение солитонов

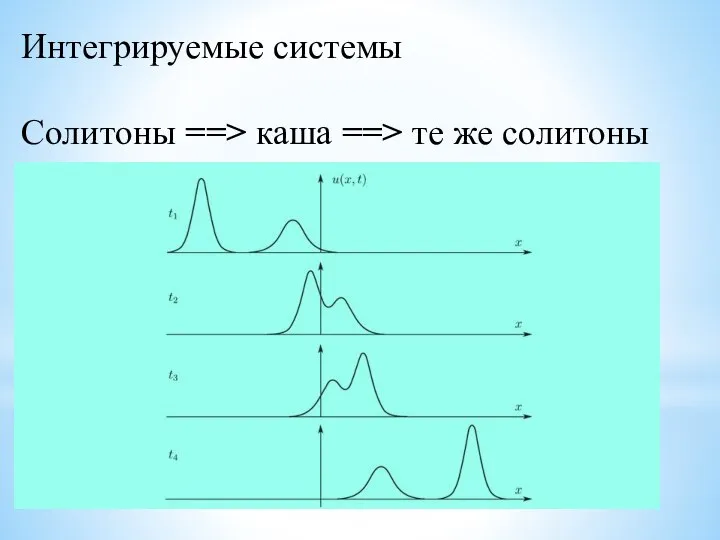
Интегрируемые системы
Солитоны ==> каша ==> те же солитоны

Общий случай
Солитоны ==> каша ==> солитоны (может быть, другие ) и почти линейный “хвостик”
("soliton resolution conjecture")

Для малых амплитуд u линейная часть подавляет нелинейную.
“Расплывание волнового пакета”
При больших временах решение приближается решением линейного уравнения (Моравец, Страусс)

Если есть солитоны, то при любых начальных данных при больших временах мы получаем суперпозицию солитонов и почти линейный хвостик.
Видимо, нетрудно доказать, что для любой асимптотики есть решение нелинейного уравнения
с этой асимптотикой.

Обобщенные солитоны - частицеподобные решения
Солитоны и квантовые частицы.
Топологические солитоны − солитоны, стабильность которых вытекает из топологических соображений
Скирм,…, Поляков,…, Тюпкин, Фатеев, Шв.

Поляков Александр Маркович

Топологические интегралы движения.
Компоненты связности пространства полей с конечной энергией.
Гомотопические классы отображений пространства Х в пространство Y − это компоненты связности бесконечномерного пространства отображений Х в Y

Минимум энергии на компоненте связности пространства полей с конечной энергией −
топологический солитон с нулевой скоростью
Топологические солитоны с ненулевой скоростью − минимумы энергии при фиксированном импульсе
Калибровочные теории. Магнитный заряд является топологическим интегралом движения.

Теории большого объединения (объединяющие электромагнитные,
слабые и сильные взаимодействия)
обязательно содержат частицы,
имеющие магнитный заряд
(магнитные монополи)
Тюпкин, Фатеев, Шв.
Монастырский, Переломов

Минимумы евклидова действия
на компонентах связности пространства полей с конечным евклидовым действием − инстантоны
Белавин, Поляков, Тюпкин, Шв.
т’Хоофт
Размерность пространства инстантонов.
Шв.
Индекс эллиптического оператора.

Топологически стабильные нити
(“почти одномерные” решения уравнений движения)
Частица может изменить свой тип,
обходя вокруг нити.
Шв.
Если в теории есть зеркальные частицы, то обходя вокруг нити, частица превращается в зеркальную (“нити Алисы”)
Нелокализованный заряд (“Чеширский заряд”)