Содержание
- 2. РАЗДЕЛ «СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ»
- 3. АКТУАЛИЗАЦИЯ ЗНАНИЙ 1.Что изучает сопротивление материалов? ответ: сопротивление материалов изучает основы прочности материалов и методы расчета
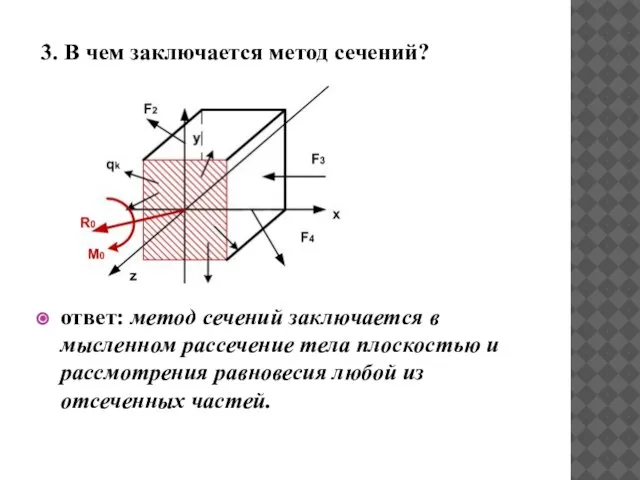
- 4. 3. В чем заключается метод сечений? ответ: метод сечений заключается в мысленном рассечение тела плоскостью и
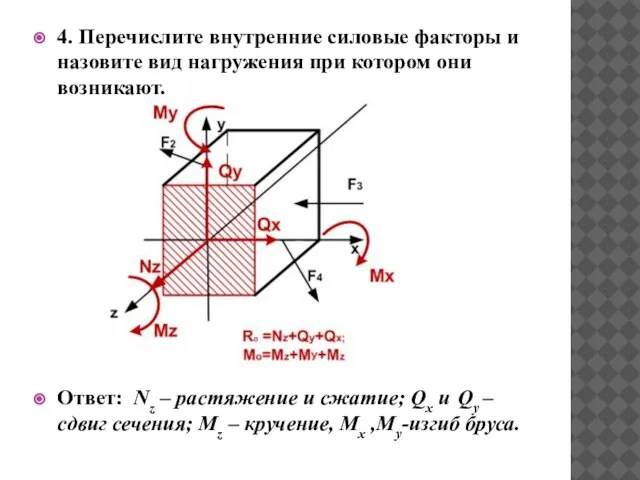
- 5. 4. Перечислите внутренние силовые факторы и назовите вид нагружения при котором они возникают. Ответ: Nz –
- 6. 4.Что называется напряжением? ответ: величина интенсивности внутренних сил называется напряжением. Напряжение характеризует величину внутренней силы приходящейся
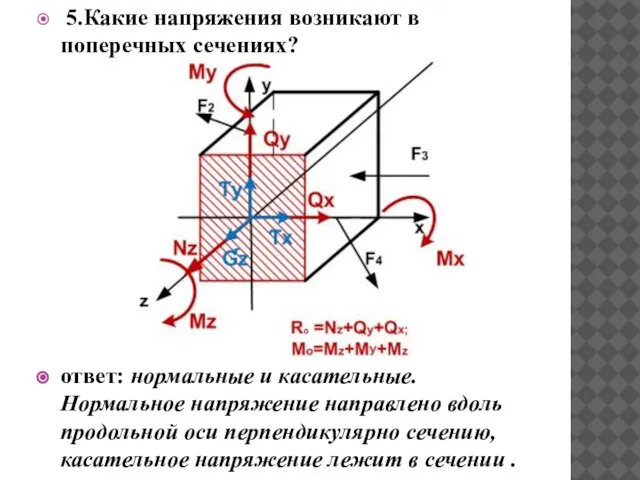
- 7. 5.Какие напряжения возникают в поперечных сечениях? ответ: нормальные и касательные. Нормальное напряжение направлено вдоль продольной оси
- 8. 6.Что называется растяжением, сжатием? ответ: растяжением, сжатием называется такой вид нагружения, при котором в поперечном сечении
- 9. 10. Что называется кручением? Ответ: Кручением называется такой вид нагружения, при котором в поперечном сечении бруса
- 10. ТЕМА: 2.5. «КРУЧЕНИЕ». План урока: 1. Внутренние силовые факторы, закон Гука при деформации «Кручение». 2. Построение
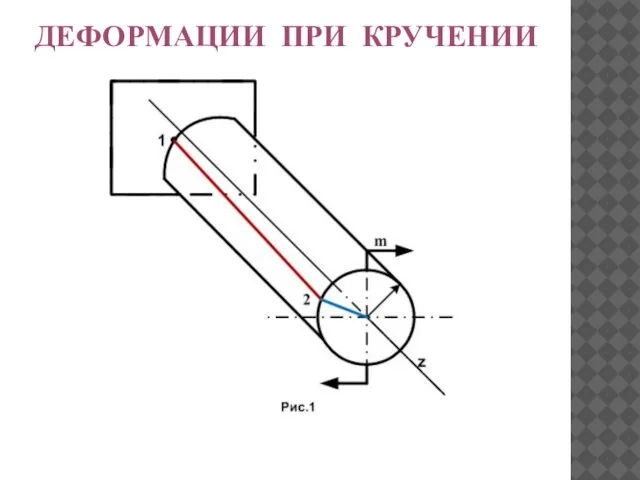
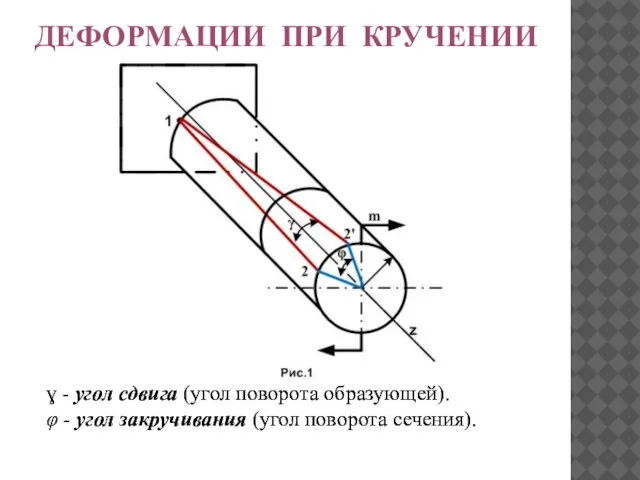
- 11. ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ
- 12. ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ ɣ - угол сдвига (угол поворота образующей). φ - угол закручивания (угол поворота
- 13. Длина бруса и размеры поперечного сечения при кручении не изменяются. Обозначим l - длина бруса; R
- 14. ГИПОТЕЗЫ ПРИ КРУЧЕНИИ 1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси,
- 15. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ ПРИ КРУЧЕНИИ Рассечем брус плоскостью I и рассмотрим равновесие отсеченной части. Крутящий момент
- 16. НАПРЯЖЕНИЯ ПРИ КРУЧЕНИИ Интенсивность распределения крутящих моментов характеризуется величиной касательных напряжений. При кручении возникает напряженное состояние
- 17. Кручением называется такой вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой
- 18. Эпюра – это график показывающий величину ВСФ вдоль всего бруса. Правила построения эпюр: 1. Разделим брус
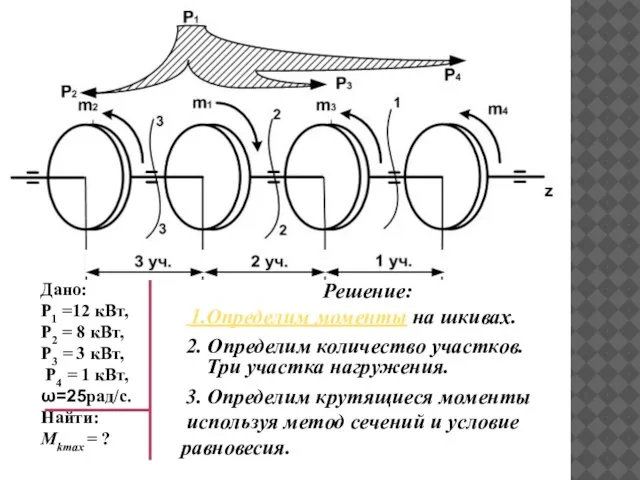
- 19. Пример. На распределительном валу установлены четыре шкива, на вал через шкив 1 подается мощность 12 кВт,
- 20. Решение: 1.Определим моменты на шкивах. 2. Определим количество участков. Три участка нагружения. Дано: Р1 =12 кВт,
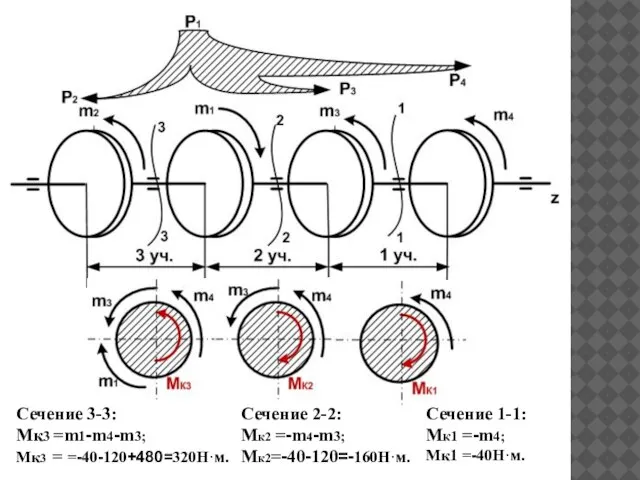
- 21. Сечение 1-1: Mк1 =-m4; Mк1 =-40Н·м. Сечение 2-2: Mк2 =-m4-m3; Mк2=-40-120=-160Н·м. Сечение 3-3: Mк3 =m1-m4-m3; Mк3
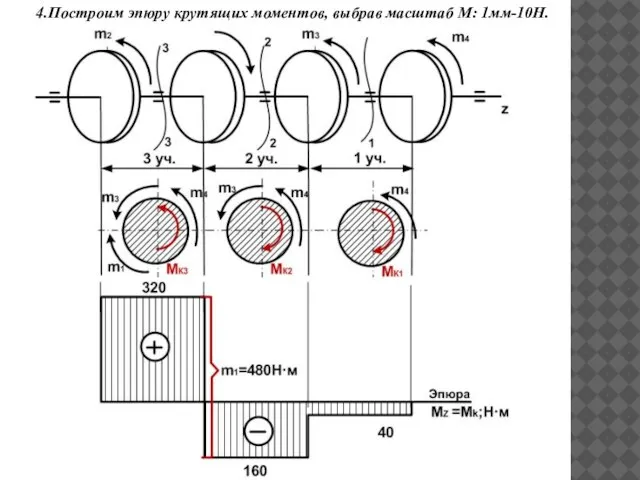
- 22. . 4.Построим эпюру крутящих моментов, выбрав масштаб М: 1мм-10Н.
- 23. Скачок на эпюре численно равен приложенному вращающему моменту. Ответ: максимальный крутящий момент на участке 3 величиной
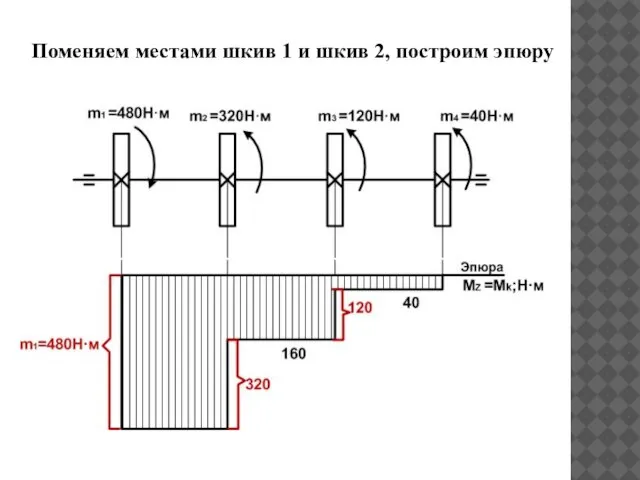
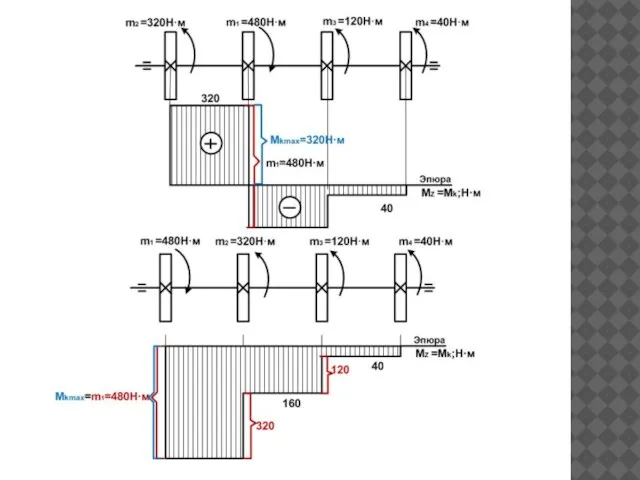
- 24. Поменяем местами шкив 1 и шкив 2, построим эпюру
- 26. Рациональным расположением шкивов на валу является такое, при котором крутящие моменты принимают минимальные из возможных значений.
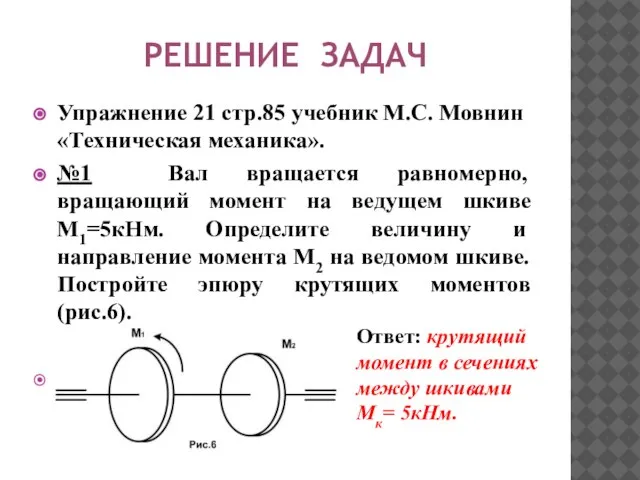
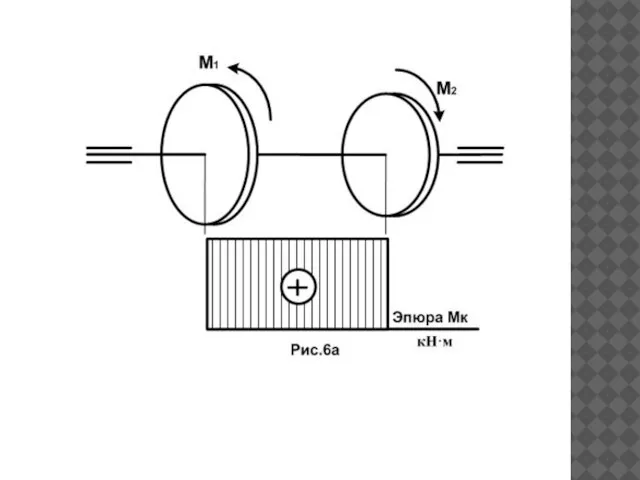
- 27. РЕШЕНИЕ ЗАДАЧ Упражнение 21 стр.85 учебник М.С. Мовнин «Техническая механика». №1 Вал вращается равномерно, вращающий момент
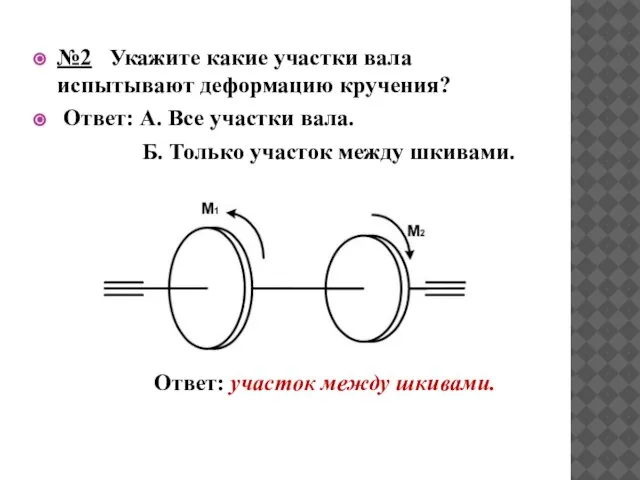
- 29. №2 Укажите какие участки вала испытывают деформацию кручения? Ответ: А. Все участки вала. Б. Только участок
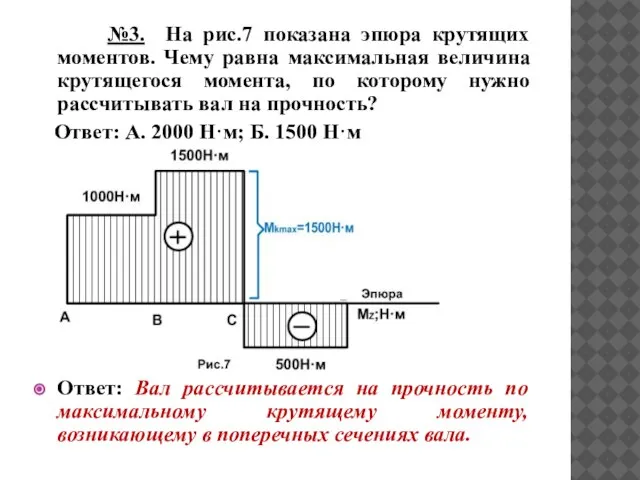
- 30. №3. На рис.7 показана эпюра крутящих моментов. Чему равна максимальная величина крутящегося момента, по которому нужно
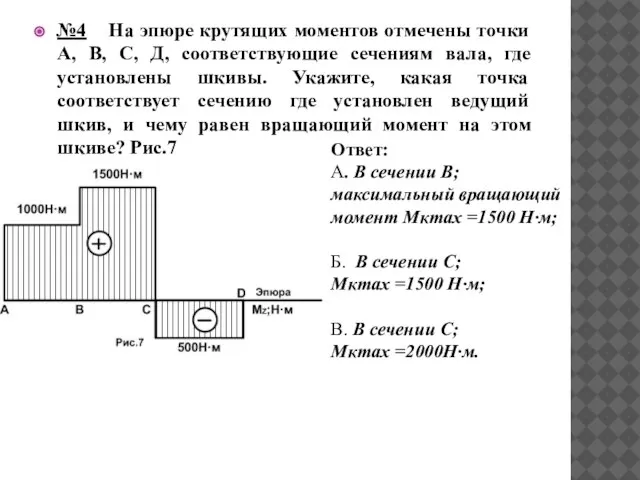
- 31. №4 На эпюре крутящих моментов отмечены точки А, В, С, Д, соответствующие сечениям вала, где установлены
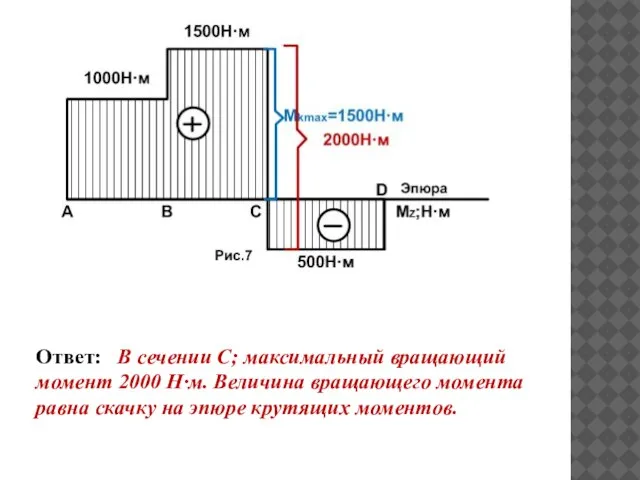
- 32. Ответ: В сечении С; максимальный вращающий момент 2000 Н·м. Величина вращающего момента равна скачку на эпюре
- 34. Скачать презентацию















 Демонстрация световых явлений на основе оптических систем
Демонстрация световых явлений на основе оптических систем Исследование деформаций в тонкостенной цилиндрической оболочке
Исследование деформаций в тонкостенной цилиндрической оболочке Манометры
Манометры Законы распространения света
Законы распространения света Что такое физическое тело? урок физики в 7 классе
Что такое физическое тело? урок физики в 7 классе Основные понятия о точности и взаимозаменяемости
Основные понятия о точности и взаимозаменяемости Динамика и устойчивость сооружений
Динамика и устойчивость сооружений Первичные и вторичные параметры длинной линии. Лекция Д1
Первичные и вторичные параметры длинной линии. Лекция Д1 Теплоемкость тела или системы
Теплоемкость тела или системы Сила трения. Виды трения. Способы изменения трения
Сила трения. Виды трения. Способы изменения трения Презентация на тему Сверхпроводимость
Презентация на тему Сверхпроводимость  28,09 7АБ физика
28,09 7АБ физика Взаимные превращения жидкостей и газов. Твёрдые тела
Взаимные превращения жидкостей и газов. Твёрдые тела Надёжность электрических машин. Надёжность контактных колец и подшипниковых узлов электрических машин
Надёжность электрических машин. Надёжность контактных колец и подшипниковых узлов электрических машин Електромагніти та їх застосування
Електромагніти та їх застосування Зубчатая передача. 5 класс
Зубчатая передача. 5 класс Влияние физики на развитие техники
Влияние физики на развитие техники Проявление законов механики
Проявление законов механики ЭКЛ _ЦРС_комп
ЭКЛ _ЦРС_комп Смазка для подшипников
Смазка для подшипников Параметрические цепи
Параметрические цепи Относительность движения
Относительность движения Механическая работа. Энергия
Механическая работа. Энергия Презентация на тему Строение и свойства вещества
Презентация на тему Строение и свойства вещества  Cокол Тысячелетия 10,08
Cокол Тысячелетия 10,08 Презентация на тему Единицы массы
Презентация на тему Единицы массы  Рефракция. Преломление света
Рефракция. Преломление света лекция 4 физика
лекция 4 физика