Содержание
- 2. Метод Бубнова-Галеркина Метод Б.Г.Галеркина (прямой метод решения краевых задач) в 1913 году был применен И.Г.Бубновым к
- 3. Метод Бубнова-Галеркина Для того, чтобы функция δ(х,у)=0, необходимо выполнение условия (4) где φ - произвольная функция,
- 4. Метод Бубнова-Галеркина (7) Разрешая систему (6) относительно αi , определим их значения и получим приближенное решение
- 5. Метод Власова Решение уравнения изгиба (1) будем искать в виде (8) где Wj- функция обобщенных прогибов,
- 6. Метод Власова где (11) Необходимо решить систему п обыкновенных дифференциальных уравнений четвертого порядка, что достаточно непросто.
- 7. Метод Ритца-Тимошенко Для построения вариационной постановки краевой задачи об изгибе пластины воспользуемся принципом минимума потенциальной энергии,
- 8. Метод Ритца-Тимошенко (15) Таким образом, необходимо исследовать на экстремум (минимум) функционал (16) Приближенное решение задачи о
- 10. Скачать презентацию







 Правило Левой руки
Правило Левой руки Ракетный двигатель. Импульс тела
Ракетный двигатель. Импульс тела Лекция 2 (Классификация САУ)
Лекция 2 (Классификация САУ) Методы астрофизических исследований. Занятие 11
Методы астрофизических исследований. Занятие 11 Презентация на тему Свойства зрения
Презентация на тему Свойства зрения  Презентация на тему Конденсаторы (10 класс)
Презентация на тему Конденсаторы (10 класс)  Электрические явления
Электрические явления М. В. Ломоносов. Его вклад в развитие физики
М. В. Ломоносов. Его вклад в развитие физики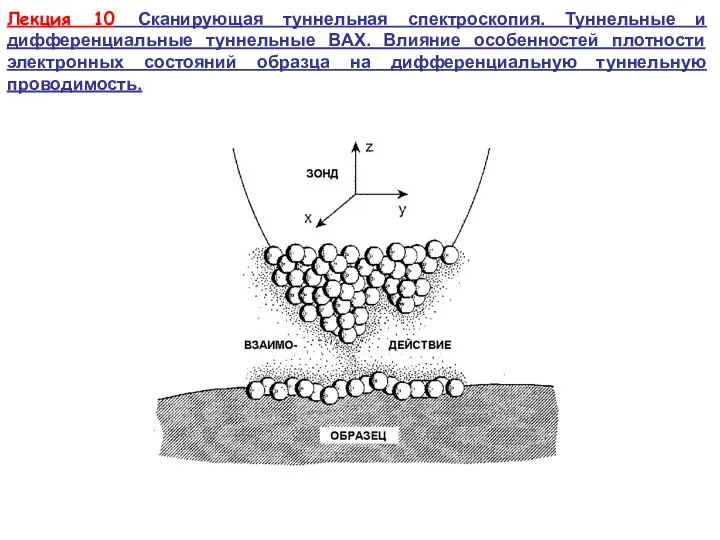 Сканирующая туннельная спектроскопия. Туннельные и дифференциальные туннельные ВАХ
Сканирующая туннельная спектроскопия. Туннельные и дифференциальные туннельные ВАХ Построение структур, обобщенные параметры, классификация и расчет составов ДНПКМ. Лекция 5
Построение структур, обобщенные параметры, классификация и расчет составов ДНПКМ. Лекция 5 Действие жидкости и газа на погруженное в них тело
Действие жидкости и газа на погруженное в них тело Силы, действующие в магнитном поле: сила Ампера, сила Лоренца
Силы, действующие в магнитном поле: сила Ампера, сила Лоренца Урок открытия нового знания (ОНЗ)
Урок открытия нового знания (ОНЗ) Электрический ток. 8 класс
Электрический ток. 8 класс Фізика. Запитання для оцінювання
Фізика. Запитання для оцінювання Лекция 42. Атомная физика
Лекция 42. Атомная физика Конфигурации (проводка) моторов HI-FINITY
Конфигурации (проводка) моторов HI-FINITY Кинематика. Операции с векторами
Кинематика. Операции с векторами Магнитный поток. Работа по перемещению проводника с током в магнитном поле
Магнитный поток. Работа по перемещению проводника с током в магнитном поле Характеристики электрического тока
Характеристики электрического тока Динамика и устойчивость сооружений
Динамика и устойчивость сооружений Магнитное поле
Магнитное поле Снегоплавилка. Идея проекта
Снегоплавилка. Идея проекта Система сходящихся сил
Система сходящихся сил Презентация на тему Снег
Презентация на тему Снег  Бесконтактная передача электроэнергии
Бесконтактная передача электроэнергии Антони ван Левенгук. Изобретатель микроскопа
Антони ван Левенгук. Изобретатель микроскопа Переменный электрический ток
Переменный электрический ток