Слайд 21. Ток проводимости в металлах, его характеристики и условия существования.
Если обозначить

через скорость упорядоченного движения (скорость дрейфа) носителей зарядов, то
- объемные плотности положительного и отрицательного зарядов.
Плотность тока и сила тока связаны соотношением:
Слайд 31. Ток проводимости в металлах, его характеристики и условия существования.
Поле
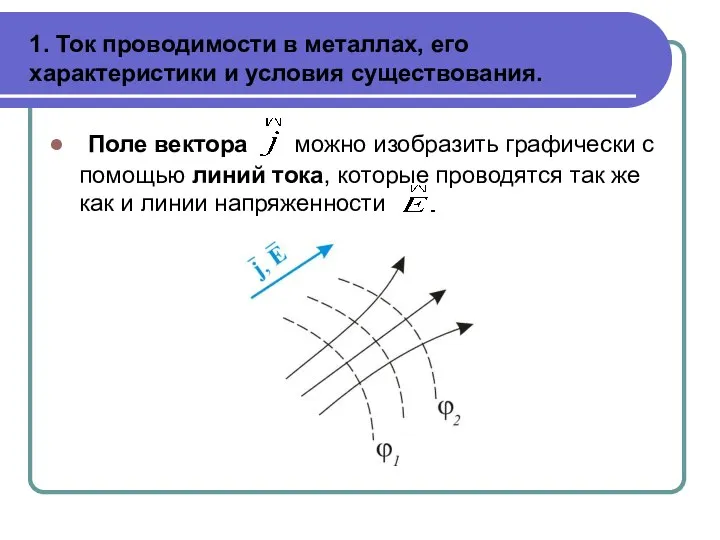
вектора можно изобразить графически с помощью линий тока, которые проводятся так же как и линии напряженности
Слайд 42. Уравнение неразрывности и условие существования постоянного тока
Представим себе в некоторой проводящей
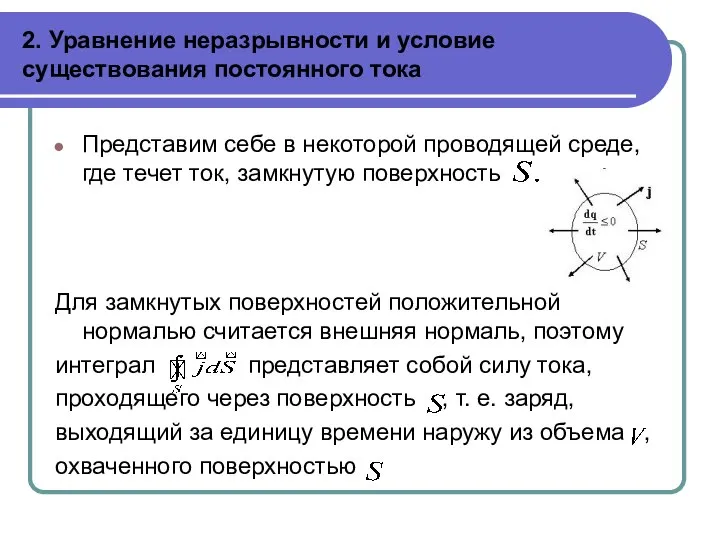
среде, где течет ток, замкнутую поверхность
Для замкнутых поверхностей положительной нормалью считается внешняя нормаль, поэтому
интеграл представляет собой силу тока,
проходящего через поверхность , т. е. заряд,
выходящий за единицу времени наружу из объема ,
охваченного поверхностью
Слайд 52. Уравнение неразрывности и условие существования постоянного тока
Из закона сохранения заряда следует,

что этот интеграл равен убыли заряда в единицу времени внутри объема
Т.е.
Данное равенство называется уравнением неразрывности (непрерывности) для эл. тока.
В случае стационарного тока
так как
Слайд 62. Уравнение неразрывности и условие существования постоянного тока
Преобразуем уравнение:
Воспользовавшись теоремой Остроградского –

Гаусса:
Слайд 72. Уравнение неразрывности и условие существования постоянного тока
уравнение неразрывности
- уравнение

неразрывности для эл.
тока в дифференциальной форме.
Для постоянного тока - условие существования постоянного тока
Слайд 82. Уравнение неразрывности и условие существования постоянного тока
Уравнение означает, что в случае

постоянного тока поле вектора не имеет источников: линии тока нигде не начинаются и нигде не заканчиваются, т. е. они замкнуты.







 Виды и источники энергии
Виды и источники энергии Урок 21+ Розв'язування задач
Урок 21+ Розв'язування задач ОМиУОИ_л1
ОМиУОИ_л1 Построение ПФ в вынужденном масштабе
Построение ПФ в вынужденном масштабе Презентация на тему Планетарная модель атома
Презентация на тему Планетарная модель атома  Популярные типы кузова автомобилей
Популярные типы кузова автомобилей Узгоджувальні пристрої. Лекція 2
Узгоджувальні пристрої. Лекція 2 Презентация по физике _Ускорение. 9 класс_
Презентация по физике _Ускорение. 9 класс_ Коэффициент трения скольжения
Коэффициент трения скольжения Законы сохранения. Самостоятельная работа
Законы сохранения. Самостоятельная работа Радиоактивность
Радиоактивность Гравитационное взаимодействие
Гравитационное взаимодействие Идеальный газ
Идеальный газ Жабдықты монтаждаудың материалдық-техникалық құралдары. Дәріс 2
Жабдықты монтаждаудың материалдық-техникалық құралдары. Дәріс 2 Презентация на тему Механическая работа и мощность (10 класс)
Презентация на тему Механическая работа и мощность (10 класс)  Импульс тела . Закон сохранения импульсов
Импульс тела . Закон сохранения импульсов Лабораторная работа Определение положения центра тяжести плоской фигуры
Лабораторная работа Определение положения центра тяжести плоской фигуры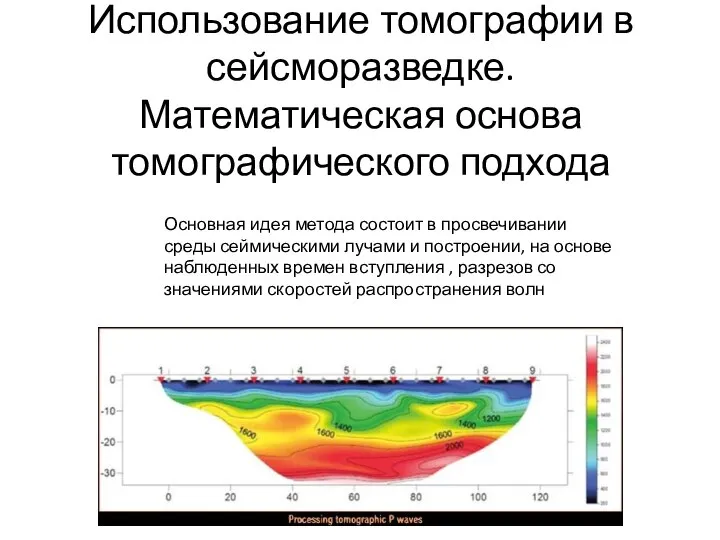 Использование томографии в сейсморазведке. Математическая основа томографического подхода
Использование томографии в сейсморазведке. Математическая основа томографического подхода Презентация на тему Электромагнитная индукция. Опыты Фарадея
Презентация на тему Электромагнитная индукция. Опыты Фарадея  Гамма- излучение
Гамма- излучение Измерительные трансформаторы напряжения
Измерительные трансформаторы напряжения Управление вертолетом. Основные моменты
Управление вертолетом. Основные моменты Решение задач по теме Закон всемирного тяготения
Решение задач по теме Закон всемирного тяготения Техническое обслуживание смазочной системы МТЗ-80
Техническое обслуживание смазочной системы МТЗ-80 Направление индукционного тока
Направление индукционного тока Электроемкость.Конденсаторы
Электроемкость.Конденсаторы Классификация помех в устройствах ЭВМ
Классификация помех в устройствах ЭВМ Косой изгиб. Построение эпюр нормальных напряжений по сечению при косом изгибе и внецентренном сжатии
Косой изгиб. Построение эпюр нормальных напряжений по сечению при косом изгибе и внецентренном сжатии