Содержание
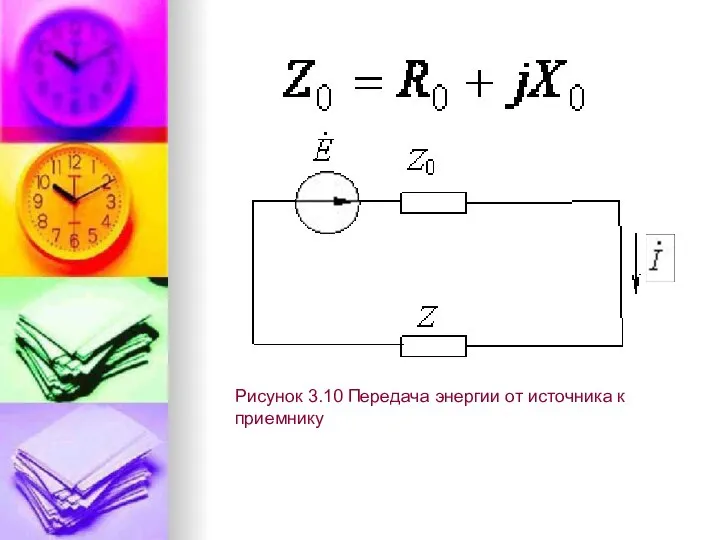
- 2. Пусть требуется подобрать комплексное сопротивление нагрузки таким образом, чтобы при заданном комплексном сопротивлении источника обеспечивалась передача
- 3. Рисунок 3.10 Передача энергии от источника к приемнику
- 4. Активная мощность, потребляемая нагрузкой, равна
- 5. Будем сначала изменять реактивное сопротивление Х. Очевидно, при любом значении R ток и соответственно средняя мощность
- 6. Найдем теперь условие максимума полученной функции в предположении, что R – переменная величина, т.е. из условия,
- 7. На основании найденных равенств заключаем, что условием передачи максимума активной мощности от источника к приемнику является
- 8. и к.п.д., определяемый, как отношение средней мощности, потребляемой приемником, к суммарной мощности, поглощаемой активными сопротивлениями цепи,
- 9. Если условие (3.17) не выполняется, то относительное отклонение передаваемой средней мощности от максимальной составляет
- 10. В тех случаях, когда реактивное сопротивление источника относительно невелико по сравнению с его активным сопротивлением, условия,
- 11. Например, при и поступающая в приемник средняя мощность отличается от максимально возможной только на 1,5%, в
- 12. Условие передачи источником максимума мощности при заданном коэффициенте мощности приёмника
- 13. На практике часто возникает необходимость подбора комплексного сопротивления нагрузки таким образом, чтобы при заданных комплексном сопротивлении
- 14. Пользуясь условными обозначениями, принятыми в предыдущем параграфе, находим полную мощность на зажимах нагрузки: где φ и
- 15. После преобразования получим: Приняв величину z за переменную, записываем условие максимума функции S
- 16. откуда или Следовательно,
- 17. Подстановка (3.19) в (3.18) дает Таким образом, передача максимума мощности в нагрузку при заданном cosφ достигается
- 18. Если условие (3.19) не соблюдается, то относительное отклонение передаваемой полной мощности от максимальной составляет . (3.20)
- 20. Скачать презентацию
















 Технологический процесс монтажа устройства для формовки протектора
Технологический процесс монтажа устройства для формовки протектора Тезаурус ВВЭР поколения 3+
Тезаурус ВВЭР поколения 3+ Линзы. Построение изображения, даваемое тонкой линзой
Линзы. Построение изображения, даваемое тонкой линзой Презентация на тему Энергия связи Дефект масс
Презентация на тему Энергия связи Дефект масс  Генератор переменного тока
Генератор переменного тока Постоянные магниты. Магнитное поле Земли
Постоянные магниты. Магнитное поле Земли Давление твёрдых тел. Давление в жидкости. Атмосферное давление
Давление твёрдых тел. Давление в жидкости. Атмосферное давление Простые механизмы
Простые механизмы Термодинамические законы
Термодинамические законы Подъемно-транспортные машины (проектирование и расчет). Расчет механизма подъема
Подъемно-транспортные машины (проектирование и расчет). Расчет механизма подъема Нанотехнологии вокруг нас
Нанотехнологии вокруг нас Свободные и вынужденные электромагнитные колебания
Свободные и вынужденные электромагнитные колебания Циклогенез и антициклогенез. Гидродинамическая теория
Циклогенез и антициклогенез. Гидродинамическая теория Давление, единицы измерения, классификация приборов давления
Давление, единицы измерения, классификация приборов давления Паровые машины. (8 класс)
Паровые машины. (8 класс) Основы технической механики
Основы технической механики Выпуск первого автомобиля в г. Тольятти
Выпуск первого автомобиля в г. Тольятти Температура и ее измерение
Температура и ее измерение Презентация на тему Внутренняя энергия. Количество теплоты
Презентация на тему Внутренняя энергия. Количество теплоты  Статика. Динамика
Статика. Динамика Волновые явления
Волновые явления Презентация на тему Броуновское движение
Презентация на тему Броуновское движение  Презентация по физике "Электродный нагревательный элемент" -
Презентация по физике "Электродный нагревательный элемент" -  Механические колебания. Виды колебаний
Механические колебания. Виды колебаний Углы установки колес автомобиля
Углы установки колес автомобиля Магнетизм
Магнетизм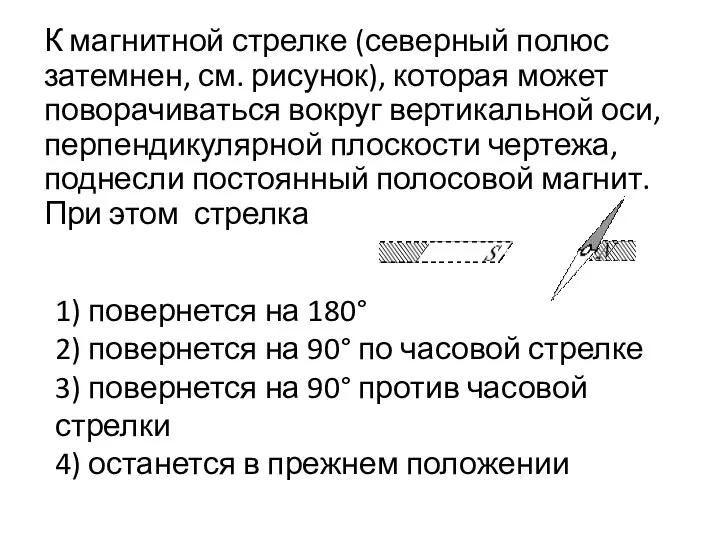 Рамка с током в магнитном поле
Рамка с током в магнитном поле Классификация тепловых двигателей
Классификация тепловых двигателей