Волновая оптика. Лекция № 3

[1] Т. И. Трофимова, §§171 –182,
185 – 187, 190-195;
«Волновая оптика»
Н. П. Калашников,
Н. М. Кожевников,
5 ДЕ, задания 21, 22.
[2] А. А. Детлаф, Б. М. Яворский,
31.1, 31.3, 32.1 – 32.5, 33.4, 33.5,
34.1, 34.2, 34,5;

Лекция № 3
Волновая оптика:
интерференция,
дифракция,
дисперсия,
поляризация

ИНТЕРФЕРЕНЦИЯ СВЕТА
Это перераспределение интен-сивности света с образованием max и min освещенности при суперпозиции (наложении) когерентных волн.

ИНТЕРФЕРЕНЦИЯ СВЕТА
Для получения когерентных световых волн свет одного источника разделяют на две системы волн путем его отражения или преломления.
Используются: метод Юнга, бипризма или бизеркало Френеля, зеркало Ллойда, тонкие пленки…

Временная – согласованность волн в данной области пространства в разные моменты времени.
типы когерентности :
‘
Пространственная – согласованность волн в разных областях в один и тот же момент времени.

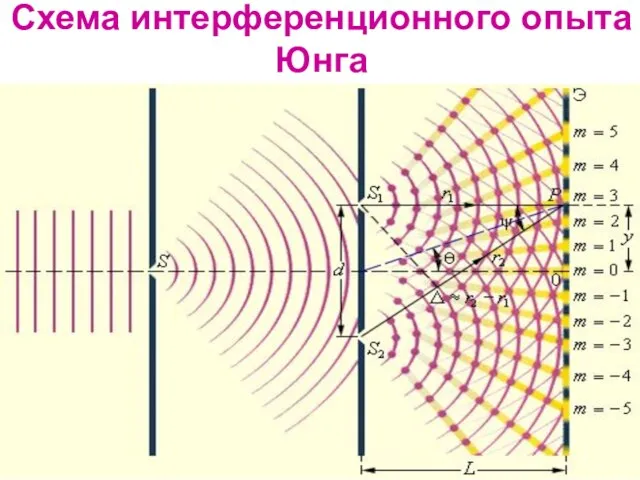
Схема интерференционного опыта
Юнга

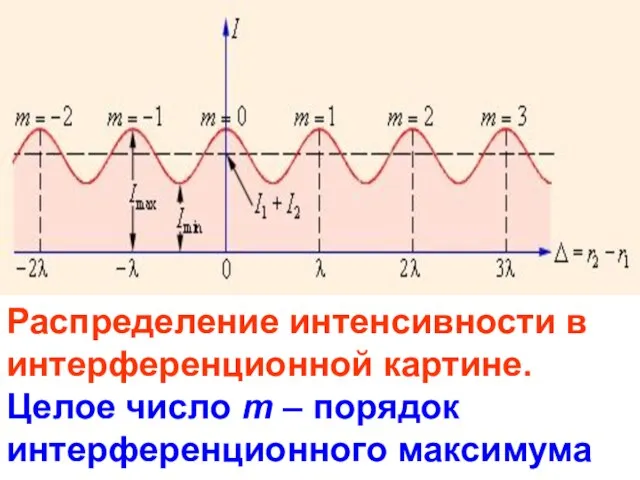
Распределение интенсивности в
интерференционной картине.
Целое число m – порядок
интерференционного максимума

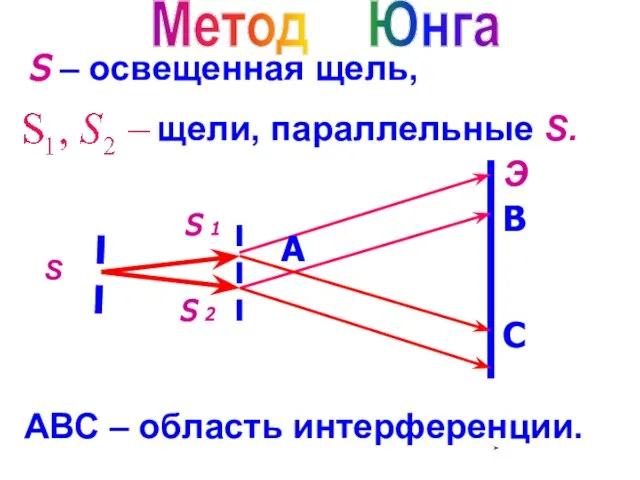
S
Э
Метод Юнга
S – освещенная щель,
щели, параллельные S.
S 1
S 2
А
В
С
АВС – область интерференции.

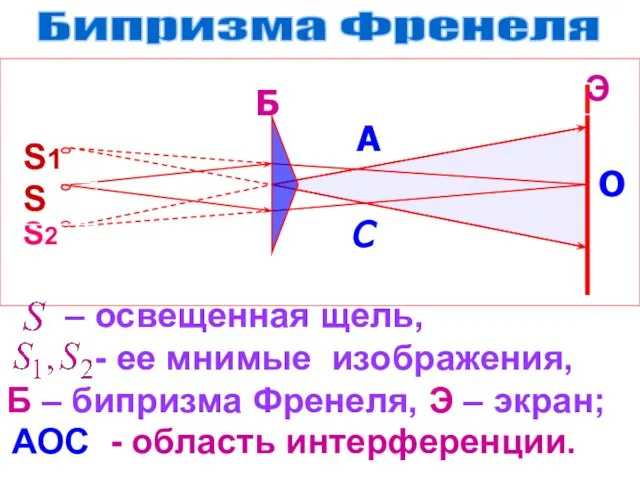
Бипризма Френеля
– освещенная щель,
- ее мнимые изображения,
Б – бипризма Френеля, Э – экран;
Б
АОС - область интерференции.
А
О
С

Геометрическая разность хода
оптическая разность хода
Условие max:
Условие min:
- целое число.

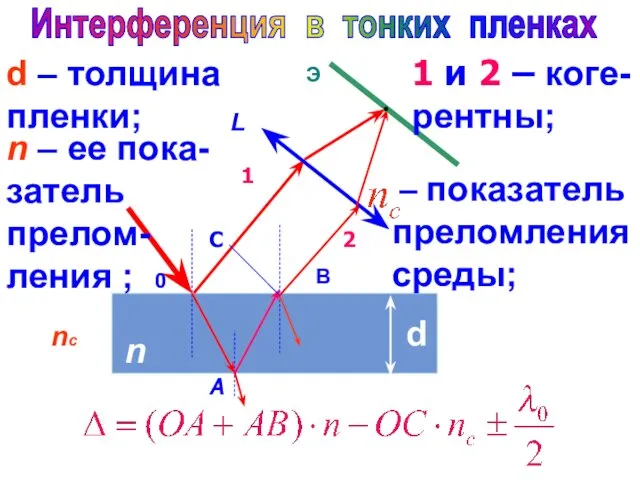
n
nс
0
B
d
L
Э
А
С
1
2
1 и 2 – коге-рентны;
– показатель преломления среды;
n – ее пока-затель прелом-ления ;
d – толщина пленки;
Интерференция в тонких пленках

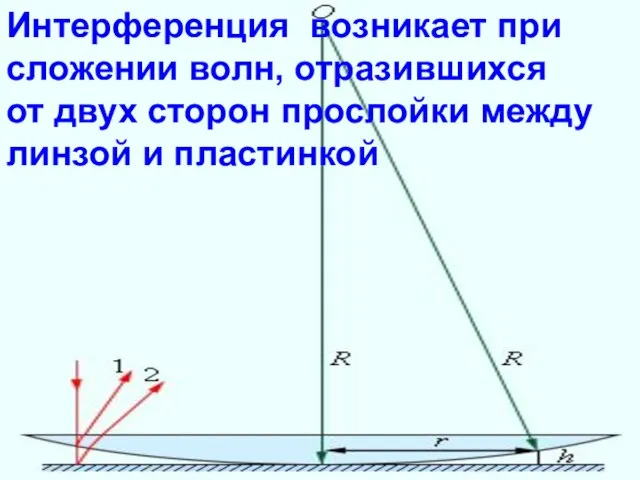
Интерференция возникает при сложении волн, отразившихся
от двух сторон прослойки между
линзой и пластинкой

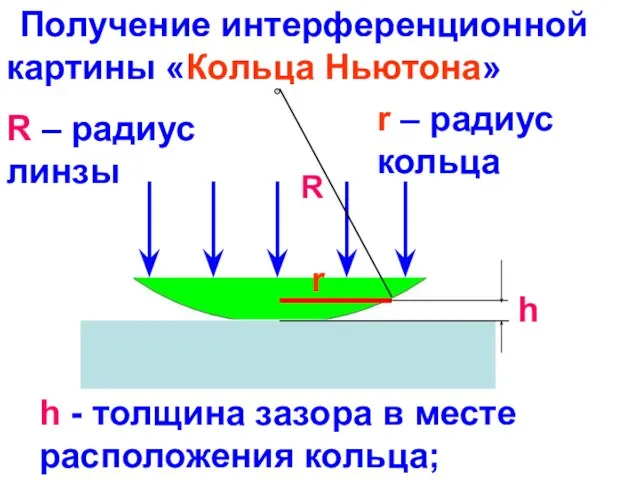
r
R
h
Получение интерференционной картины «Кольца Ньютона»
R – радиус
линзы
r – радиус кольца
h - толщина зазора в месте расположения кольца;

Расчет радиуса колец
R
r
h
R-h
1
2
оптическая разность
хода;
- радиус светлого кольца;
m = 1,2,3,… - целое число.
Отраженный свет

Расчет радиуса колец
R
r
h
R-h
1
2
- радиус темного кольца.
m=1,2,3,… - целое число;
Отраженный свет

Радиус
кольца
зависит
от
длины
волны
света

Это явление огибания световой волной границ непрозрачных тел с интерференционным перераспределением энергии.
ДИФРАКЦИЯ СВЕТА

Дифракция Френеля:
фронт волны – сферический или плоский; на экране, находящемся на конечном расстоянии от пре-пятствия, «дифракционное изображение» препятствия.

Дифракция Фраунгофера:
фронт волны - плоский;
на экране, находящемся в
фокальной плоскости линзы, “ дифракционное изображе-ние” удаленного источника света.

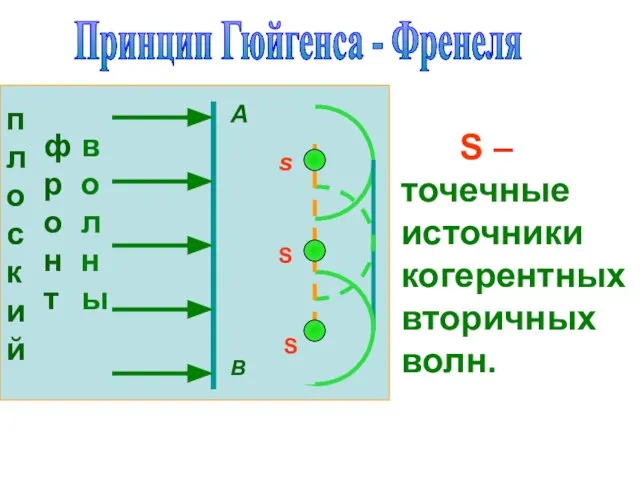
Принцип Гюйгенса - Френеля
А
В
s
S
S
S – точечные источники когерентных вторичных волн.
плоский
фронт
волны

Каждая точка среды, до которой
дошел волновой фронт, стано-вится точечным источником вторичных волн. Принцип Гюйгенса - Френеля
Для электромагнитных волн
наличие среды необязательно.

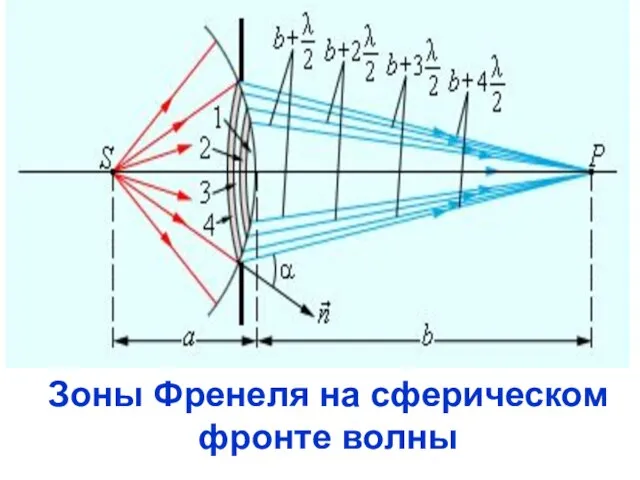
Зоны Френеля на сферическом
фронте волны

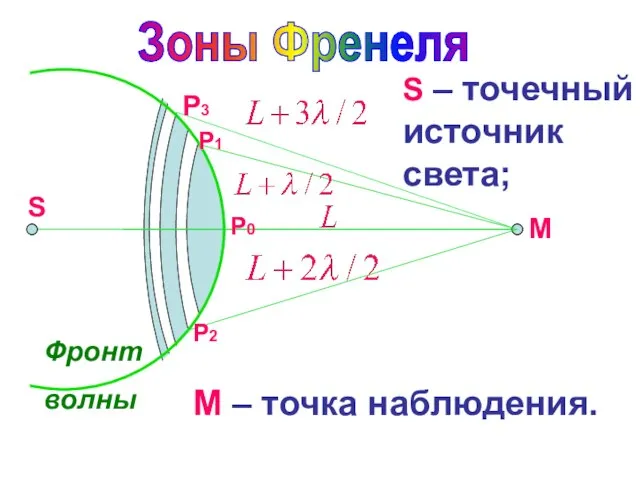
S
Фронт
волны
Р0
Р1
Р2
Р3
Зоны Френеля
М
S – точечный источник света;
М – точка наблюдения.

Это участки волновой поверхно-сти, на которые она мысленно разбивается. Площади зон
примерно одинаковы. Колебания, возбуждаемые в точке М соседни-ми зонами, противоположны по фазе (гасят друг друга).

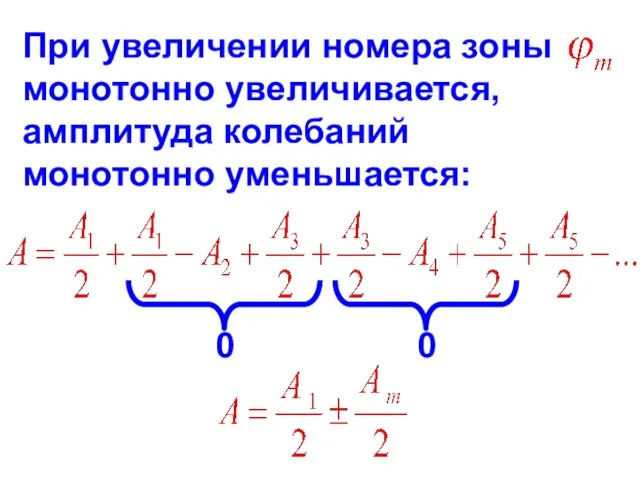
При увеличении номера зоны
монотонно увеличивается,
амплитуда колебаний
монотонно уменьшается:
0
0

Радиус m-ой зоны:
а) сферической волны
б) плоской волны

Дифракция на круглом
отверстии

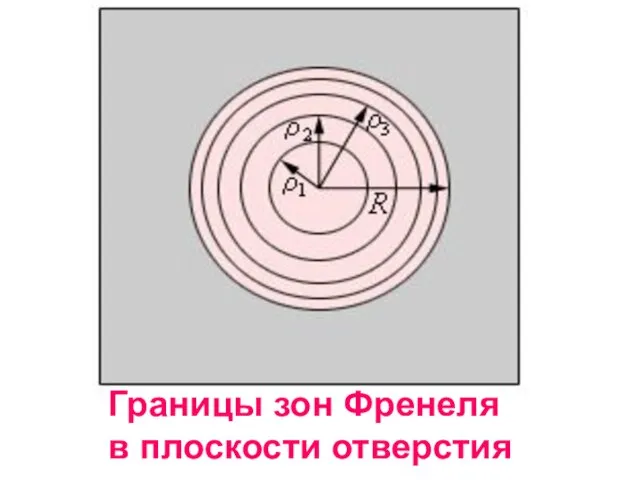
Границы зон Френеля
в плоскости отверстия

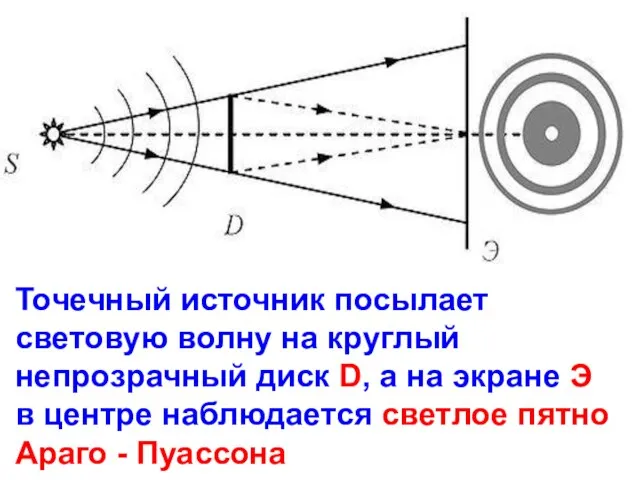
Точечный источник посылает
световую волну на круглый
непрозрачный диск D, а на экране Э
в центре наблюдается светлое пятно
Араго - Пуассона

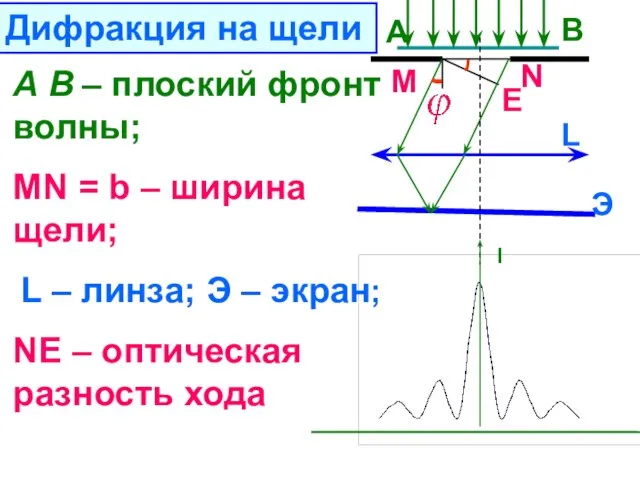
L
А
В
А В – плоский фронт волны;
MN = b – ширина щели;
L – линза; Э – экран;
NE – оптическая разность хода
I
Дифракция на щели

Условие min при дифракции
на щели
m = 1 , 2 , 3 . . . – порядок дифракционного минимума
- угол дифракции;

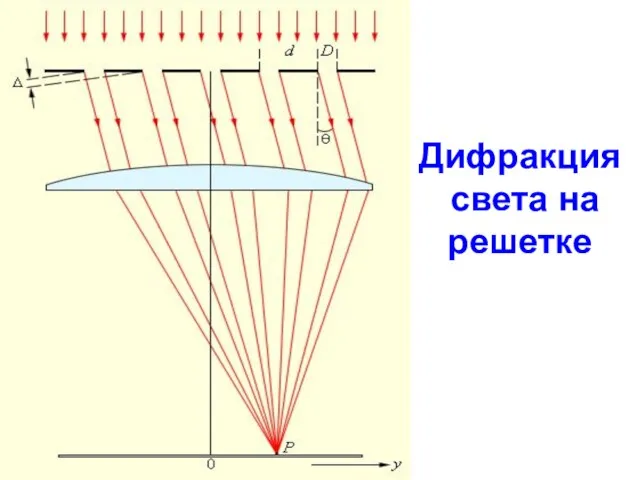
Дифракция
света на
решетке

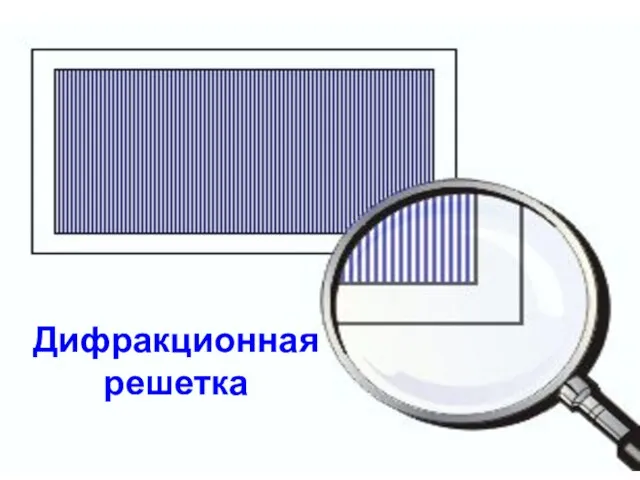
Дифракционная
решетка

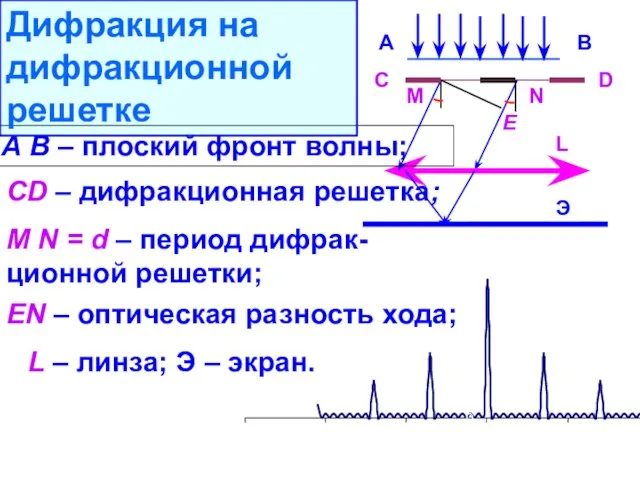
Э
С
D
E
M
N
А
В
L
А В – плоский фронт волны;
CD – дифракционная решетка;
M N = d – период дифрак-ционной решетки;
EN – оптическая разность хода;
L – линза; Э – экран.
Дифракция на
дифракционной
решетке

m = 0 , 1 , 2 , 3 . . .
m = 1, 2 , 3 . . .
Условие главных максимумов:
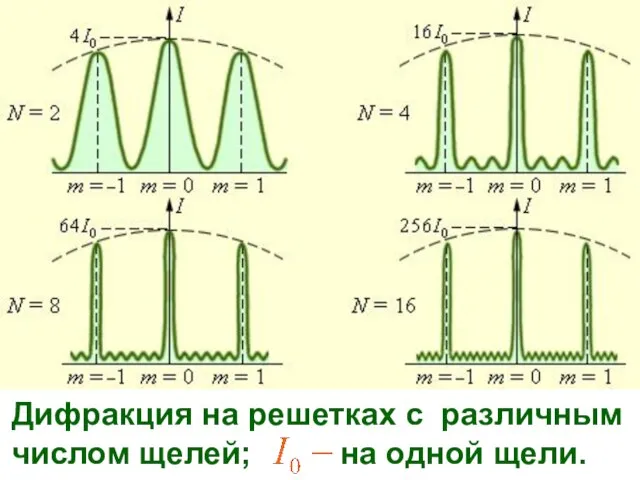
Условие главных минимумов:

Дифракция на решетках с различным
числом щелей; на одной щели.

Разложение белого света
в спектр с помощью
дифракционной решетки

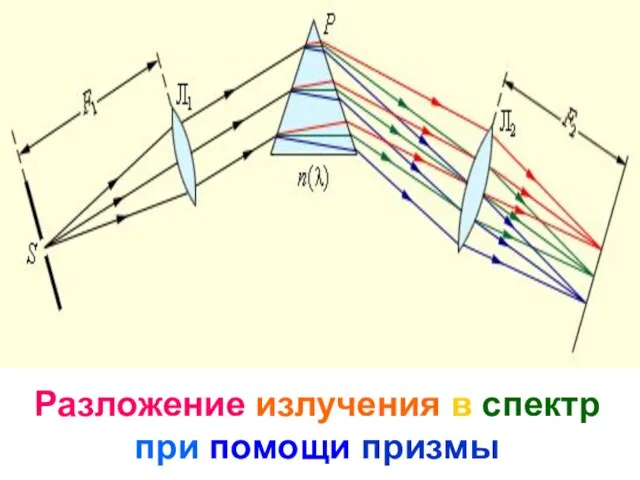
Разложение излучения в спектр
при помощи призмы

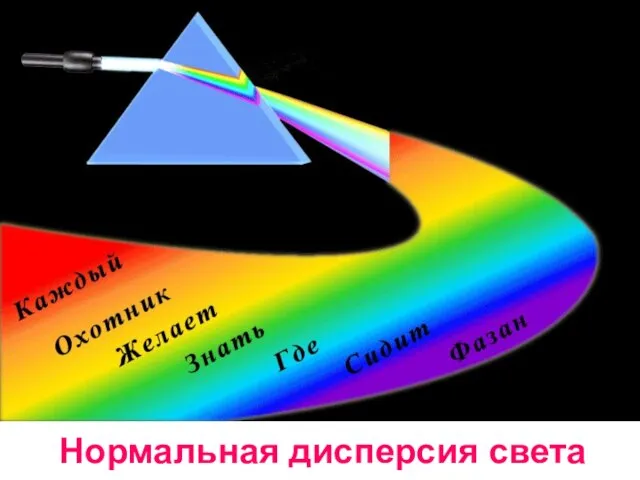
Нормальная дисперсия света

Радуга.
Дисперсия
света на водяных
каплях

Дисперсия света в кристаллах
льда

Зависимость показателя прелом-
ления от частоты имеет вид
При изменении от 0 до
2) при
3) при изменении от

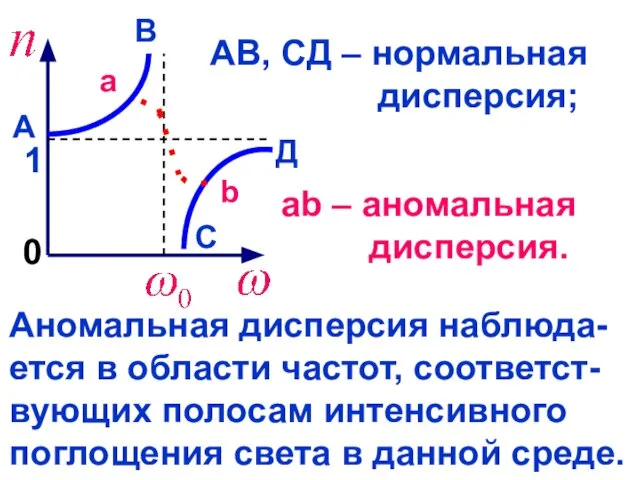
0
1
А
В
С
Д
АВ, СД – нормальная
дисперсия;
ab – аномальная
дисперсия.
a
b
Аномальная дисперсия наблюда-
ется в области частот, соответст-
вующих полосам интенсивного
поглощения света в данной среде.

Выводы
1) Свет – ЭМ волна;
2) диапазоны: УФ - видимый - ИК;
3) док- во: явления
интерференции, дифракции,
дисперсии; поперечность
световой волны подтверждает
явление поляризации.

П О Л Я Р И З А Ц И Я
СВЕТА
получение света, в котором
колебания вектора каким-
либо образом упорядочены.
Вектор напряженности электрического поля называют световым вектором.

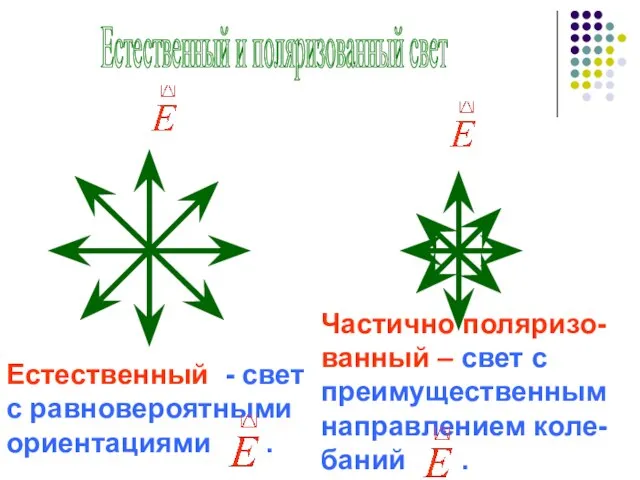
Естественный и поляризованный свет
Естественный - свет с равновероятными ориентациями .
Частично поляризо-ванный – свет с преимущественным направлением коле-баний .

Степень поляризации
где I max, I min – максимальная и минимальная интенсивности поляризованного света.
Р = 0 – для естественного света;
P = 1- для поляризованного света.

Получение поляризованного света
При отражении и преломлении на границе раздела двух изотропных сред.
При прохождении света через анизотропную среду (двойное лучепреломление).
типы поляризации

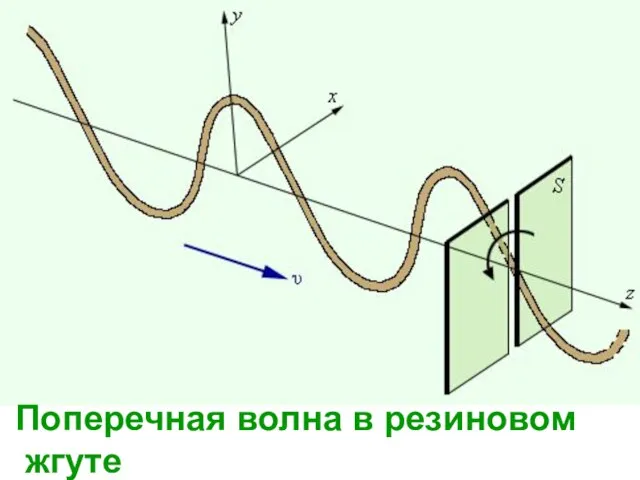
Поперечная волна в резиновом
жгуте

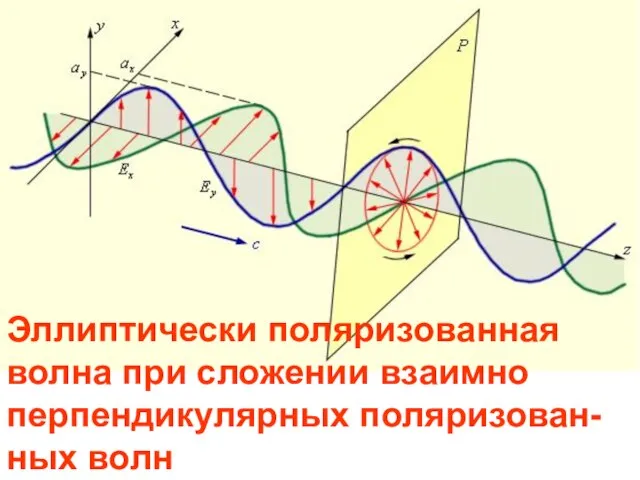
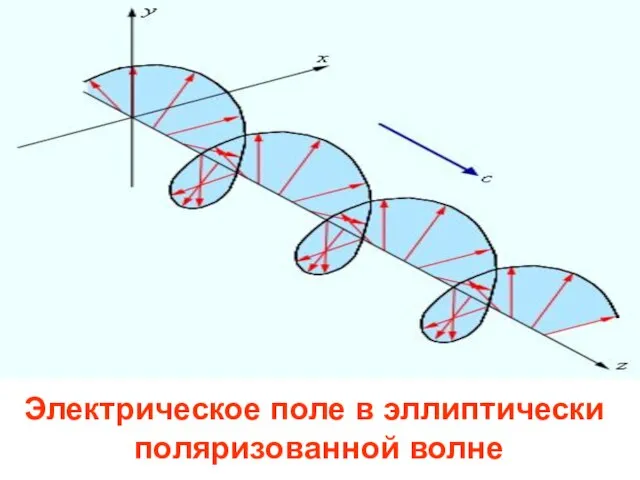
Эллиптически поляризованная волна при сложении взаимно перпендикулярных поляризован-ных волн

Электрическое поле в эллиптически
поляризованной волне

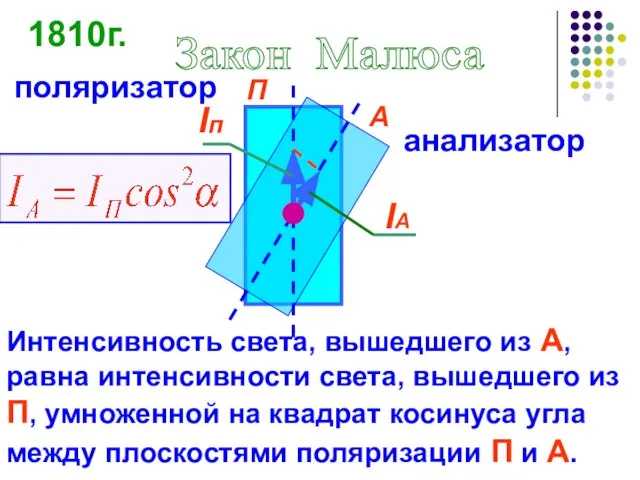
Iп
IА
П
А
Интенсивность света, вышедшего из А, равна интенсивности света, вышедшего из П, умноженной на квадрат косинуса угла между плоскостями поляризации П и А.
поляризатор
анализатор
Закон Малюса
1810г.

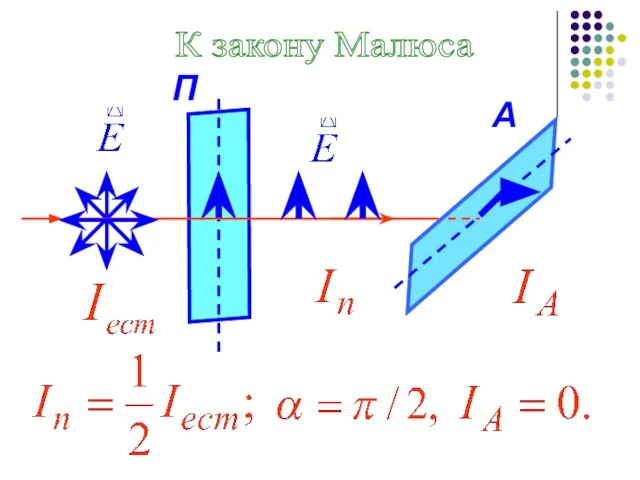
П
А
К закону Малюса

- без учета потерь света в П и А;
- коэффициенты погло-щения света П и А.

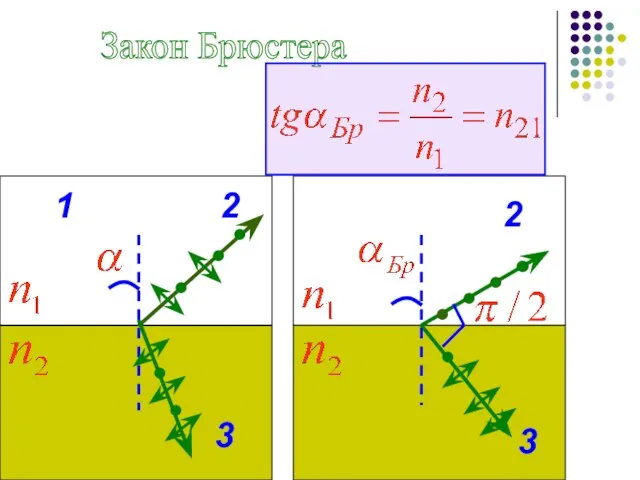
Закон Брюстера
1
2
3
2
3

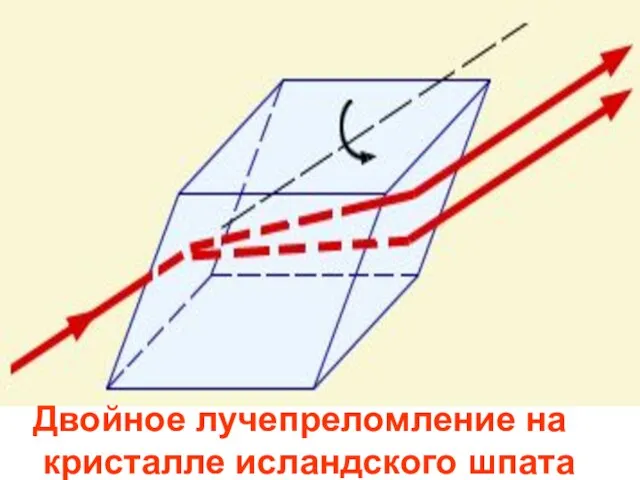
Двойное лучепреломление на
кристалле исландского шпата