Содержание
- 2. План лекции Закон всемирного тяготения. Теорема Гаусса. Гравитационное поле однородного шара. Финитные и инфинитные движения. Космические
- 3. Уравнение моментов для частицы и системы частиц dL/dt = M = [rF] – скорость изменения момента
- 4. Закон сохранения момента импульса относительно точки dL/dt = M = 0 → L = const Если
- 5. Движение частицы в центральном поле сил Центральная сила зависит только от расстояния r до силового центра
- 6. Связь импульса с секториальной скоростью dS = ½ [rdr] = ½ [rv]dt σ = dS/dt =
- 7. Закон всемирного тяготения Материальные точки притягиваются с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату
- 8. Напряжённость гравитационного поля Напряжённость поля тяготения g(r) = F/m = -GM/r2 r/r g(r) = g0R2/r2 Принцип
- 9. Теорема Гаусса Поток вектора g через любую замкнутую поверхность равен полной массе внутри поверхности, умноженной на
- 10. Гравитационные поля в простейших случаях Плоскость (σ = m/S – поверхностная плотность): g = -2πGσ Цилиндр
- 11. Энергия сил гравитационного взаимодействия U = ∫Fdr = -GMm/r U = ∫Fdr = -GMm/r = -
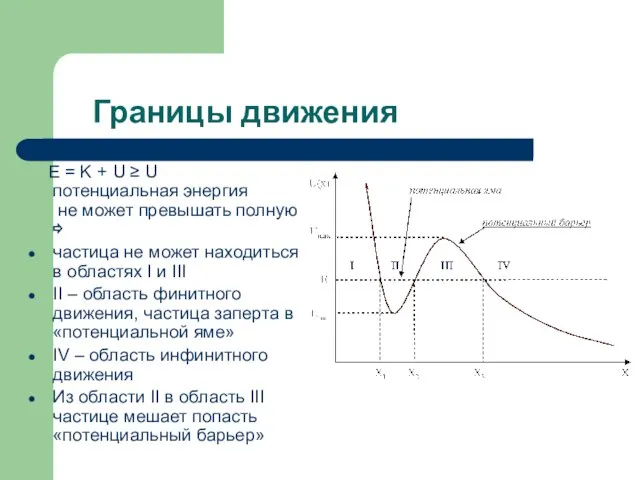
- 12. Границы движения E = K + U ≥ U потенциальная энергия не может превышать полную ⇨
- 13. Космические скорости Первая космическая – скорость кругового движения на околоземной орбите: vI = (g0R)1/2 = 7,9
- 15. Законы Кеплера Каждая планета движется по эллипсу, в одном из фокусов которых находится Солнце Радиус-вектор планеты
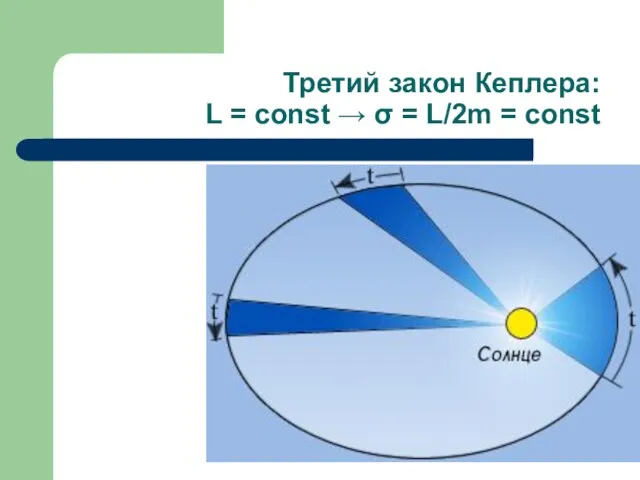
- 16. Третий закон Кеплера: L = const → σ = L/2m = const
- 17. Параметры эллиптической орбиты Радиус круговой орбиты: r = GM/2|ε| Большая п/ось эллипса: a = GM/2|ε| Малая
- 18. Третий закон Кеплера mv2/2 – GmM/r = E = const → r2 + GMr/ε – L2/2m2
- 19. Спутник связи - стационарный спутник: Tc = 24 часа. r = ? Период спутника связи Tc
- 20. Орбита Земли – эллипс? В каких пределах изменяется расстояние от Земли до Солнца? Когда мы к
- 21. Что длиннее, - полярный день или полярная ночь? Дни летнего и зимнего солнцестояния (22 июня и
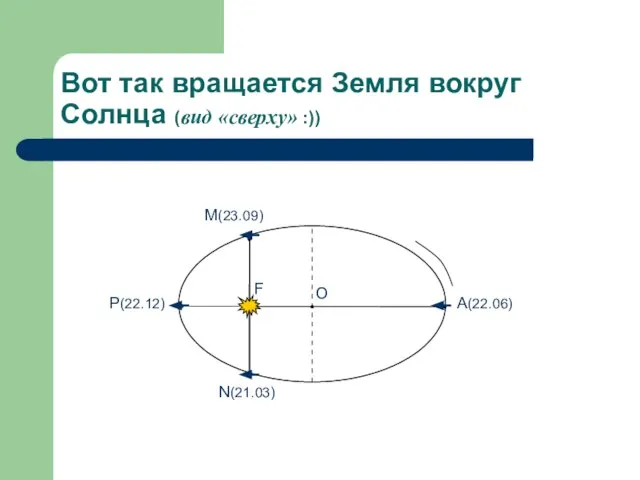
- 22. F O A(22.06) P(22.12) M(23.09) N(21.03) Вот так вращается Земля вокруг Солнца (вид «сверху» :))
- 23. Решаем Эллиптичность не велика ⇨ TS/T0 ≈ (πR2/2+ 2FR)/πR2 = ½ + 2F/πR TW/T0 ≈ (πR2/2
- 24. Заглянем в таблицу Vmax (в перигелии) = 30,3 км/с Vmin (в афелии) = 29,3 км/с ΔV
- 25. От Земли по разным траекториям С полюса Земли запускают ракету со скоростью v0: vI вертикально вверх
- 26. Пример 2. Время падения Луны на Землю ☺ Сколько времени будет падать на Землю Луна, если
- 27. Сила сопротивления разгоняет(?) спутник Полная энергия на круговой орбите E = К + П = К
- 28. Скорость снижения спутника Спутник массой m = 200 кг, запущенный на круговую околоземную орбиту, тормозится в
- 29. Маневры на орбите: чтобы догнать – надо притормозить! чтобы отстать – надо ускориться! Корабль и орбитальная
- 30. Полёт на Марс (№ 7.6) Рассчитайте время перелёта с орбиты Земли на орбиту Марса (rм =
- 31. Метеорит. Прицельное расстояние Скорость метеорита на большом расстоянии от Земли V0. Найти наибольшее «прицельное» расстояние b
- 33. Скачать презентацию

![Уравнение моментов для частицы и системы частиц dL/dt = M = [rF]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/866895/slide-2.jpg)


![Связь импульса с секториальной скоростью dS = ½ [rdr] = ½ [rv]dt](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/866895/slide-5.jpg)






















 Электромагнитная индукция. Опыты Фарадея
Электромагнитная индукция. Опыты Фарадея Всесвітнє тяжіння тіл
Всесвітнє тяжіння тіл История Ультразвукового Контроля
История Ультразвукового Контроля Термодинамика Термодинамика (Волькенштейн-1990) Первое начало термодинамики 5.162 5.165 5.186 5.185 5.159 5.170 5.182 Второе начало терм
Термодинамика Термодинамика (Волькенштейн-1990) Первое начало термодинамики 5.162 5.165 5.186 5.185 5.159 5.170 5.182 Второе начало терм задачи на равноускоренное движение (1)
задачи на равноускоренное движение (1) Плотность вещества
Плотность вещества Физика для одноклассников
Физика для одноклассников Молекулярная физика и термодинамика
Молекулярная физика и термодинамика Диагностирование генератора
Диагностирование генератора 1 начало термодинамики для изопроцессов
1 начало термодинамики для изопроцессов Теория ядерных реакторов
Теория ядерных реакторов Закон сохранения импульса. Реактивное движение
Закон сохранения импульса. Реактивное движение Измерение массы медицинского шприца (без иглы)
Измерение массы медицинского шприца (без иглы) Складові похибок вимірювання. Тема 4
Складові похибок вимірювання. Тема 4 Презентация на тему Введение в космологию
Презентация на тему Введение в космологию 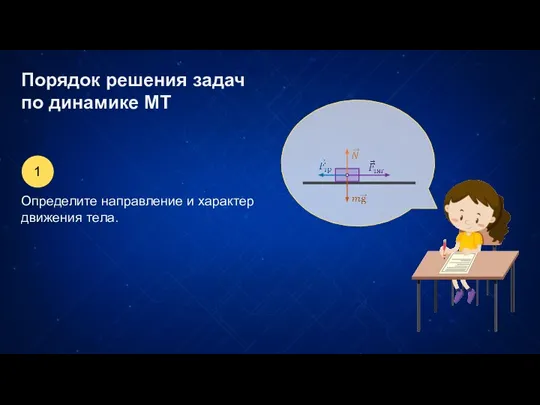 Порядок решения задач по динамике МТ
Порядок решения задач по динамике МТ Ретро стиль. Восстановление и ремонт ретро автомобилей. Ремонт современных легковых автомобилей
Ретро стиль. Восстановление и ремонт ретро автомобилей. Ремонт современных легковых автомобилей Радиоволны. История открытия
Радиоволны. История открытия Электромагнитные колебания
Электромагнитные колебания Механическое движение
Механическое движение Явления электромагнитной индукции
Явления электромагнитной индукции Звёздный час. Игра по физике
Звёздный час. Игра по физике Метрология
Метрология Законы Ньютона
Законы Ньютона Технология обработки металлов (6 класс)
Технология обработки металлов (6 класс) Основы квантовой статистики и физики твердого тела. Лекция 1: Основные понятия теории твердого тела
Основы квантовой статистики и физики твердого тела. Лекция 1: Основные понятия теории твердого тела История создания швейной машины
История создания швейной машины Проводники и диэлектрики в электростатическом поле
Проводники и диэлектрики в электростатическом поле