Основные понятия и аксиомы динамики. Понятие о трении

Аксиомы динамики
Законы динамики обобщают результаты многочисленных опытов и наблюдений. Законы динамики, которые принято рассматривать как аксиомы, были сформулированы Ньютоном, но первый и четвертый законы были известны Галилею. Механику, основанную на этих законах, называют классической механикой.
Первая аксиома (принцип инерции):
Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.
Это состояние называют состоянием инерции. Вывести точку из этого состояния, т. е. сообщить ей некоторое ускорение, может внешняя сила.
Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела.
Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы — килограмм (кг).
Вторая аксиома (второй закон Ньютона — основной закон динамики)
Зависимость между силой, действующей на материальную точку, и сообщаемым ею ускорением следующая:
F = та,
где т — масса точки, кг; а — ускорение точки, м/с2.
Ускорение, сообщенное материальной точке силой, пропорционально величине силы и совпадает с направлением силы.
Основной закон динамики в дифференциальной форме:

На все тела на Земле действует сила тяжести, она сообщает телу ускорение свободного падения, направленное к центру Земли:
G = тg,
где g = 9,81м/с2, ускорение свободного падения.
Третья аксиома (третий закон Ньютона).
Силы взаимодействия двух тел равны по величине и
направлены по одной прямой в разные стороны (рис. 13.1):
Откуда
При взаимодействии ускорения обратно пропорциональны массам.
Четвертая аксиома (закон независимости действия сил).
Каждая сила системы сил действует так, как она действовала бы одна.
Ускорение, сообщаемое точке системой сил, равно геометрической сумме ускорений, сообщенных точке каждой силой в отдельности (рис. 13.2):

Понятие о трении. Виды трения
Трение — сопротивление, возникающее при движении одного шероховатого тела по поверхности другого. При скольжении тел возникает трение скольжения, при качении — трение качения. Природа сопротивлений движению в разных случаях различна.
Трение скольжения.
Причина — механическое зацепление выступов. Сила сопротивления движению при скольжении называется силой трения скольжения (рис. 13.3а).
Законы трения скольжения:
Сила трения скольжения прямо пропорциональна
силе нормального давления:
Fтр = Ff = fR,
где R — сила нормального давления,
направлена перпендикулярно опорной поверхности;
f — коэффициент трения скольжения.
В случае движения тела по наклонной плоскости (рис. 13.3, б)
R = Gcosα,
где α — угол наклона плоскости к горизонту.
Сила трения всегда направлена в сторону, обратную направлению движения

Сила трения меняется от нуля до некоторого максимального
значения, называемого силой трения покоя
(статическое трение):
0 < Ff ≤ Ffo
Ff0 — статическая сила трения (сила трения покоя).
Сила трения при движении меньше силы трения покоя.
Сила трения при движении называется динамической силой трения (Ff):
Ff ≤ Ffo
Поскольку сила нормального давления,
зависящая от веса и направления опорной
поверхности, не меняется, то различают статический и динамический коэффициенты трения:
Ff = fR; Ff0 = f0R.
Коэффициент трения скольжения зависит от следующих факторов:
от материала: материалы делятся на фрикционные (с большим коэффициентом трения) и антифрикционные (с малым коэффициентом трения), например f = 0,1 – 0,15 (при скольжении стали по стали всухую), f = 0,2 – 0,3 (при скольжении стали по текстолиту);
от наличия смазки, например f = 0,04 – 0,05 (при скольжении стали по стали со смазкой);
от скорости взаимного перемещения.

Трение качения
Сопротивление при качении связано с взаимной деформацией
грунта и колеса и значительно меньше трения скольжения.
Обычно считают грунт мягче колеса, тогда в основном деформируется
грунт, и в каждый момент колесо должно перекатываться через выступ
грунта. Для равномерного качения колеса необходимо прикладывать
силу FДВ (рис. 13.4).
Условие качения колеса состоит в том, что движущийся момент должен
быть не меньше момента сопротивле­ния:
где k — максимальное значение плеча (половина колеи) принимается за коэффициент трения качения, размерность — сантиметры.
Ориентировочные значения k (определяются экспериментально): сталь по стали — k — 0,005 см; резиновая шина по шоссе — k = 0,24 см.
Примеры решения задач
Пример 1. Свободная материальная точка, масса которой 5 кг, движется согласно уравнению S = 0,48t2+0,2t. Определить величину движущей силы.
Решение
1. Ускорение точки: a = v' = S"; v = S' = 0,96t + 0,2; a = v' = 0,96 м/с2.
2. Действующая сила согласно основному закону динамики F = ma; F = 5 * 0,96 = 4,8 Н.

Пример 2. Тело массой т = 2 кг движется по гладкой горизонтальной поверхности согласно уравнению S = 2t3 (S — в метрах, (t — в секундах). Определить силу Р в конце второй се­кунды после начала дви­жения.
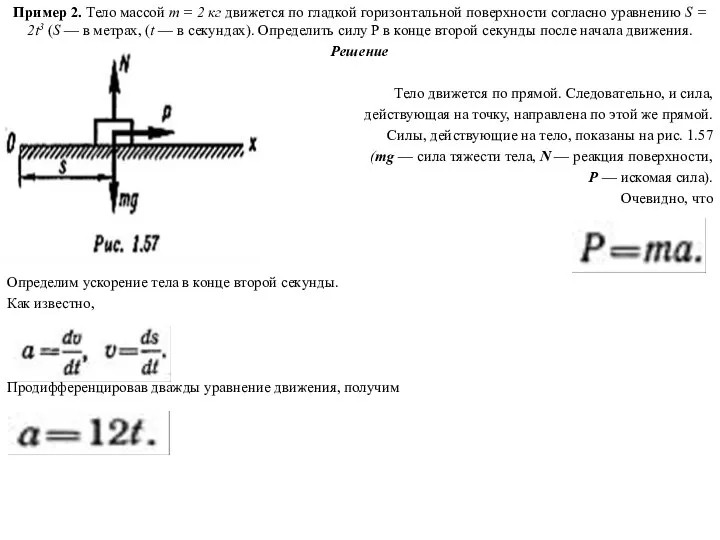
Решение
Тело движется по прямой. Следовательно, и сила,
действующая на точку, направлена по этой же прямой.
Силы, действующие на тело, показаны на рис. 1.57
(тg — сила тяжести тела, N — реакция по­верхности,
Р — искомая сила).
Очевидно, что
Определим ускорение тела в конце второй секунды.
Как известно,
Продифференцировав дважды уравнение движения, по­лучим

Ускорение тела в конце второй секунды
Тогда
Пример 3. К двум материальным точкам массой m1 = 2 кг и m2 = 5 кг приложены одинаковые силы. Сравнить величины уско­рений.
Решение
Согласно третьей аксиоме динамики ускорения обратно пропор­циональны массам:
a1 /a2 = m2/m1 = 5/2 = 2,5
a1 = 2,5 a2
Пример 4. На материальную точку действует система
сил (рис. 13.5). Определить числовое значение ускорения,
полученного материальной точкой m = 7 кг.
Остальные данные представлены на чертеже.
Решение
1-й вариант.
Определяем суммарную силу, действующую на точку:

Определяем ускорение, сообщенное точке:
a∑ = 28/7 = 4 м/с2
2-й вариант.
Определяем ускорения от каждой из сил системы (рис. 13.5, б):
а1 = 10/7 = 1,43 м/с2, а2 = 15/7 = 2,14 м/с2; а3 = 20/7 = 2,86 м/с2.
2. Определяем суммарное ускорение:
Пример 4. Материальная точка, сила тяжести ко­торой G = 100 Н, движется по прямолинейной гладкой поверхности (рис. 1.58) с ускорением а = 1,5 м/с2. Опре­делить силу Р, вызывающую движение, пренебрегая силами сопротивления.
Решение
Задано движение материальной точки, требу­ется определить
движущую силу (прямая задача динами­ки). На материальную
точку действуют три силы: сила тяжести G, реакция гладкой
горизонтальной плоскости N и движущая сила Р.
Силы G и N уравновешены, следовательно, основное уравнение
динамики в этом случае имеет вид:

Подставляя числовые значения, получаем
Пример 5. Под действием силы тяжести тело М падает с высоты H = 1500 м, испытывая сопротивление воздуха. Полагая силу сопротивления постоянной и равной половине силы тяжести, найти ускорение тела а и скорость V через 5с после начала движения, если начальная скорость V0 = 0 (рис. 1.59).
Решение
В данном случае силы заданы, требуется определить кинематические
характеристики движения: ускорение, скорость
(об­ратная задача динамики). По основному уравнению получим
Откуда
Рассматриваемое тело движется равномерно-ускоренно, а = const = 4,9 м/с2.
Скорость точки при равномерно-ускоренном движении определяется по формуле

В рассматриваемом примере v0 = 0, следовательно, v = at.
В конце пятой секунды после начала движения ско­рость точки
Определим время падения тела.
При равномерно-ускоренном движении
Поскольку v0 = 0, получаем
Откуда
Итак, через 24,7 с тело упадет на землю

Пример 6. В шахте опускается равномерно-уско­ренно бадья, сила тяжести которой Q = 280 кН. В первые 10 с она проходит путь S = 35 м. Найти натяжение каната, на котором висит бадья (рис. 1.60).
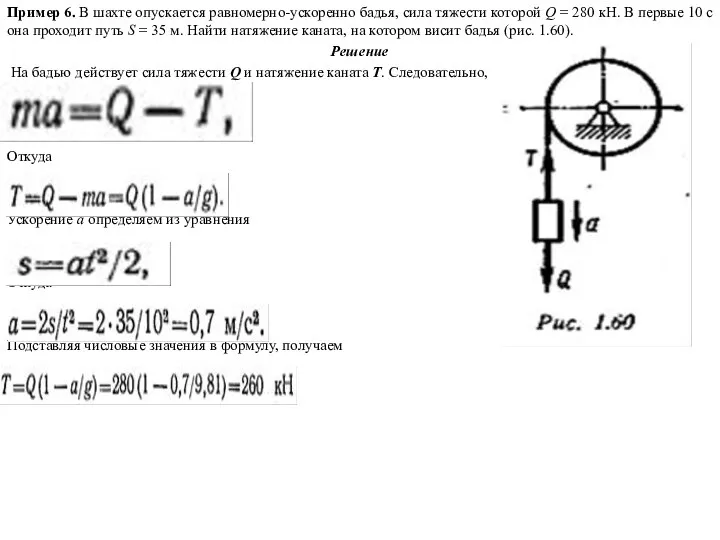
Решение
На бадью действует сила тяжести Q и натяжение каната Т. Следовательно,
Откуда
Ускорение а определяем из уравнения
Откуда
Подставляя числовые значения в формулу, получаем