Слайд 7Момент импульса
Поле, в котором сила взаимодействия направлена по соединяющей тела прямой, называется

центральным. Примерами могут служить гравитационное и электростатическое поля. В центральном поле, в силу параллельности радиус-вектора тела и силы взаимодействия момент импульса всегда сохраняется. Поэтому тело в центральном поле всегда двигается в одной плоскости, к которой перпендикулярен вектор момента импульса, что значительно упрощает задачу нахождения траектории тела.
Напомним, что задача двух тел сводится к задаче о движения тела с приведенной массой вокруг «закрепленного» центра. Поэтому в дальнейшем мы будем считать, что центр поля неподвижен. Мы ограничимся рассмотрением одного центрального поля – гравитационного.
Слайд 8Энергия частицы в гравитационном поле.

Слайд 9Энергия частицы в гравитационном поле.

Слайд 10Энергия частицы в гравитационном поле

Слайд 11Энергия частицы в гравитационном поле
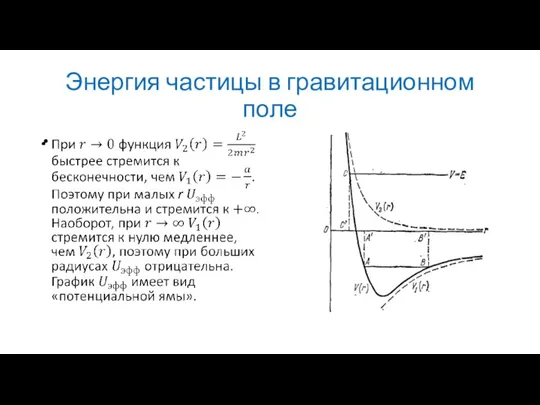
Слайд 12Энергия частицы в гравитационном поле

Слайд 13Иоганн Кеплер и Тихо Браге
Тихо Браге - 14 декабря 1546, Кнудструп, Дания

(ныне на территории Швеции) — 24 октября 1601, Прага) — датский астроном, астролог и алхимик эпохи Возрождения. Первым в Европе начал проводить систематические и высокоточные астрономические наблюдения, на основании которых Кеплер вывел законы движения планет.
Слайд 14Иоганн Кеплер и Тихо Браге
Будучи великолепным наблюдателем, Тихо Браге за много лет

составил объёмный труд по наблюдению планет и сотен звёзд, причём точность его измерений была существенно выше, чем у всех предшественников. Для повышения точности Браге применял как технические усовершенствования, так и специальную методику нейтрализации погрешностей наблюдения. Особо ценной была систематичность измерений
Слайд 15Иоганн Кеплер и Тихо Браге
Ио́ганн Ке́плер (нем. Johannes Kepler; 27 декабря 1571 года,

Вайль-дер-Штадт — 15 ноября 1630 года, Регенсбург) — немецкий математик, астроном, механик, оптик и астролог, первооткрыватель законов движения планет Солнечной системы.
Слайд 16Иоганн Кеплер и Тихо Браге
На протяжении нескольких лет Кеплер внимательно изучает данные

Браге и в результате тщательного анализа приходит к выводу, что траектория движения Марса представляет собой не круг, а эллипс, в одном из фокусов которого находится Солнце — положение, известное сегодня как первый закон Кеплера.
Дальнейший анализ привёл ко второму закону: радиус-вектор, соединяющий планету и Солнце, в равное время описывает равные площади. Это означало, что чем дальше планета от Солнца, тем медленнее она движется. В 1618 году Кеплер открыл третий закон: отношение куба среднего удаления планеты от Солнца к квадрату периода обращения её вокруг Солнца есть величина постоянная для всех планет: a³/T² = const.
Слайд 17Законы Кеплера
1). Планеты Солнечной системы обращаются по эллипсу, в одном из фокусов

которых находится Солнце.
2). Каждая планета движется в плоскости, проходящей через центр Солнца, причем за равные времена радиус-вектор, соединяющий Солнце и планету, «заметает» равные площади.
3). Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет.
Нашей задачей будет вывод этих законов из закона всемирного тяготения.
Слайд 18Первый закон Кеплера - Доказательство

Слайд 19Первый закон Кеплера - Доказательство

Слайд 20Первый закон Кеплера - Доказательство

Слайд 21Первый закон Кеплера - Доказательство
В аналитической геометрии доказывается, что уравнение описывает конические

сечения, т.е. кривые, по которым поверхность круглого конуса пересекается плоскостью). Величины p и e называются параметром и экцентриситетом орбиты. В зависимости от величины e получаются следующие кривые:
Слайд 22Первый закон Кеплера
e = 0. В этом случае получается круг. Энергия в

этом случае равна минимуму эффективного потенциала.
e < 1 – получается эллипс, что, собственно доказывает первый закон Кеплера. Энергия в этом случае меньше нуля, движение финитно.
e = 1 – это парабола (E = 0)
e > 0 – это гипербола. В двух последних случаях движение инфинитно.
Эти рассуждения доказывают первый закон Кеплера.
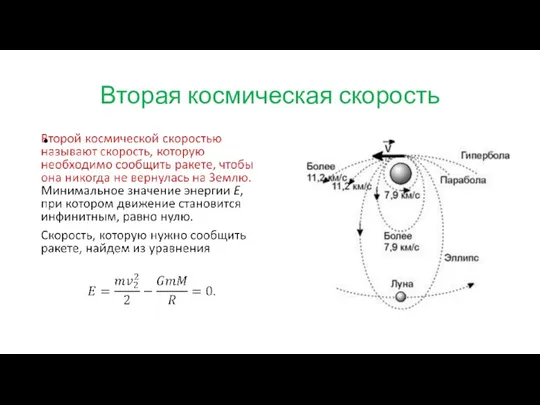
Слайд 26Космические скорости
Изложенная в предыдущем разделе теория движения планет полностью применима к движению

искусственных спутников Земли и космических кораблей (с выключенными двигателями). Сопротивление воздуха мы не будем учитывать, предполагая, что движение происходит в достаточно разреженной атмосфере. Кроме того, при движении вблизи Земли мы будем пренебрегать силами притяжения Солнца, Луны и планет. Массу Земли будем обозначать M, массу искусственного спутника m.
Слайд 29Геостационарный спутник
Связь через геостационарные спутники характеризуется большими задержками в распространении сигнала. При

высоте орбиты 35786 км и скорости света около 300000 км/с ход луча «Земля-спутник» требует около 0,12 с. Ход луча «Земля (передатчик) → спутник → Земля (приемник)» ≈0,24 с. Ping (ответ) составит полсекунды (точнее 0,48 с). С учетом задержки сигнала в аппаратуре ИСЗ и аппаратуре наземных служб общая задержка сигнала на маршруте «Земля → спутник → Земля» может достигать 2—4 секунд. Такая задержка делает невозможной применение спутниковой связи с использованием ГСО в различных сервисах реального времени (например в онлайн-играх).
Слайд 30Геостационарный спутник
Так как геостационарная орбита не видна с высоких широт (приблизительно от

81° до полюсов), а на широтах выше 75° наблюдается очень низко над горизонтом (в реальных условиях спутники просто скрываются выступающими объектами и рельефом местности) и виден лишь небольшой участок орбиты, то невозможна связь и телетрансляция с использованием ГСО в высокоширотных районах Крайнего Севера (Арктики) и Антарктиды. К примеру, американские полярники на станции Амундсен-Скотт для связи с внешним миром (телефония, интернет) используют оптоволоконный кабель длиной 1670 километров до расположенной на 75° ю.ш. французской станции Конкордия, с которой уже видно несколько американских геостационарных спутников
Слайд 34Задача 1
Оценить, с какой минимальной скоростью нужно стартовать с поверхности Луны, чтобы

вернуться на Землю. Ускорение свободного падения на Луне равно g/6, скорость движения Луны по орбите 1 км/с, радиус Луны 1740 км.
Слайд 35Задача 1 - решение
После выхода из поля тяготения Луны корабль должен перейти

на эллиптическую орбиту вокруг Земли, у которой высота перигея равна радиусу Земли RЗ, а высота апогея равна расстоянию Земля-Луна RЗ-Л
Слайд 39Неинерциальные системы отсчета. Неинерциальные силы
До сих пор мы рассматривали движение тел относительно

инерциальных систем отсчета, в которых справедливы Законы Ньютона. Но Земля, например, является неинерциальной вращающейся системой. Вследствие этого на ее поверхности возникают явления, требующие для своего понимания изучение закономерностей движения тел в движущихся с ускорением системах. Проанализируем эти закономерности.
Слайд 41Поступательное движение
Eсли движение рассматривается относительно системы отсчета, ускоренно движущейся относительно инерциальной системы

отсчета, то во втором законе Ньютона, кроме реальной силы, появляется дополнительное слагаемое - ma0. Это сила, имеющая чисто кинематическое происхождение, пропорциональная массе тел (как и гравитационная сила). Такие силы называют силами инерции. Они появляются в неинерциальных системах отсчета.
Слайд 42Поступательное движение
Пример: тележка, движущуюся с ускорением а0, на которой стоит подставка с

висящим на нитке грузиком.
Найдем угол отклонения грузика от вертикали и частоту колебаний этого маятника
Слайд 45Центробежная сила
Вследствие вращения Земли вокруг своей оси связанные с Землёй системы отсчёта

не являются инерциальными. В точке, находящейся на расстоянии a от оси вращения, центробежное ускорение равно ω2a, где ω — угловая скорость вращения Земли, определяемая выражением ω = 2π/T, в котором Т — время одного оборота (звёздные сутки), равное для Земли 86164,1 секунды. Центробежное ускорение направлено от оси вращения. Можно подсчитать, что на Земле оно меняется от 0 на полюсах до 3,4 см/с2 на экваторе, причём почти везде (кроме экватора) оно не сонаправлено с гравитационным ускорением, которое направлено к центру Земли.
Слайд 47Сила Кориолиса
Сила Кориолиса проявляется в глобальных масштабах. В северном полушарии сила Кориолиса

направлена вправо от движения, поэтому правые берега рек в Северном полушарии более крутые — их подмывает вода под действием этой силы. В Южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за вращение циклонов и антициклонов в Северном полушарии вращение воздушных масс происходит в циклонах против часовой стрелки, а в антициклонах по часовой стрелке; в Южном— наоборот: по часовой стрелке в циклонах и против — в антициклонах. Отклонение ветров (пассатов) при циркуляции атмосферы— также проявление силы Кориолиса.
Слайд 48Задача 2
Тело свободно падает с высоты 500 м на землю. Принимая во

внимание вращение Земли и пренебрегая сопротивлением воздуха, определить, насколько отклонится тело при падении. Географическая широта места 60°.
















































 Магнитные свойства материалов
Магнитные свойства материалов Внедрение гибридных солнечно-ветровых систем электропитания для развития ИКТ в предгорных населенных пунктах и регионах
Внедрение гибридных солнечно-ветровых систем электропитания для развития ИКТ в предгорных населенных пунктах и регионах Устойчивость упругих систем
Устойчивость упругих систем Архимедова сила. Решение задач
Архимедова сила. Решение задач Механика. Введение
Механика. Введение Расчет сложных цепей постоянного тока
Расчет сложных цепей постоянного тока Закон сохранения электрического заряда. Закон Кулона
Закон сохранения электрического заряда. Закон Кулона Ясси электромагнит тўлқин ва унинг хоссалари. Элeктромагнит тўлқин шкаласи
Ясси электромагнит тўлқин ва унинг хоссалари. Элeктромагнит тўлқин шкаласи Определение эффекта Томпсона
Определение эффекта Томпсона Электроемкость. Электроемкость конденсатора. Энергия конденсатора
Электроемкость. Электроемкость конденсатора. Энергия конденсатора Насыщенный пар. Кипение. Влажность воздуха. Уроки физики в 10 классе
Насыщенный пар. Кипение. Влажность воздуха. Уроки физики в 10 классе Закон преломления света
Закон преломления света Электромагнитная индукция. Опыты Фарадея
Электромагнитная индукция. Опыты Фарадея МотоСкороХоды
МотоСкороХоды Вещества в электрическом поле
Вещества в электрическом поле Расчет мачты на оттяжках в системе SCAD (из руководства по расчету мачт)
Расчет мачты на оттяжках в системе SCAD (из руководства по расчету мачт) Презентация по физике "Проблемное обучение в преподавании физики" -
Презентация по физике "Проблемное обучение в преподавании физики" -  Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса 967e92b4b9644313ad5ce02418b68434
967e92b4b9644313ad5ce02418b68434 Задачи на тему: Простые механизмы
Задачи на тему: Простые механизмы Презентация на тему Свойства твёрдых тел
Презентация на тему Свойства твёрдых тел  Физические основы исследования электрических полей в организме. Электрокардиография
Физические основы исследования электрических полей в организме. Электрокардиография 02_Основные электрические величины и их единицы измерений
02_Основные электрические величины и их единицы измерений Технология. Ядерная энергия
Технология. Ядерная энергия Солнечные батареи: принцип работы и применение
Солнечные батареи: принцип работы и применение Классификация методов осаждения вакуумных покрытий
Классификация методов осаждения вакуумных покрытий Кипение воды
Кипение воды Пара сил
Пара сил