Аэрологические оптические шар-пилотные наблюдения

Одной из основных задач аэрологических измерений является получение информации о параметрах ветра и их распределении с высотой.

Для измерения скорости и направления ветра в атмосфере могут быть использованы различные методы, однако наиболее широко применяется метод , когда для получения информации о ветре в ее значительной нижней части (тропосфере и стратосфере) используются наблюдения за перемещением объектов (трассеров), которые одновременно перемещаются в горизонтальном и в вертикальном направлениях.

Перемещение в горизонтальном направлении осуществляется за счет движения воздушных потоков, а в вертикальном направлении — либо за счет силы Архимеда, либо за счет силы земного притяжения.
Трассерами могут являться:
- шары-пилоты, в качестве которых обычно используют оболочки, наполненные газами легче воздуха (зондирование снизу вверх),
- специальные мишени, опускающиеся на парашютах (зондирование сверху вниз).

Определение скорости и направления ветра при этом основано на измерении изменений координат таких трассеров за определенный интервал времени.
По временным интервалам между измерениями координат могут быть рассчитаны средняя скорость ветра и его направление в слое атмосферы, толщина которого определяется вертикальной скоростью перемещения объекта и интервалами времени между смежными отчетами.

В зависимости от способа определения координат перемещающегося объекта в атмосфере можно выделить три разновидности данного метода:
- оптический,
- радиотехнический,
- навигационный.

При осуществлении оптического метода наблюдения за перемещением объекта в атмосфере выполняются с помощью специальных угломерных приборов — аэрологических теодолитов.
Радиотехнический метод предполагает измерение координат объекта с помощью специальных радиотехнических устройств — радиотеодолитов или радиолокационных станций.
В навигационном методе положение объекта в атмосфере определяется с помощью спутниковых навигационных систем (ранее - сигналов специальных навигационных наземных станций) .

Среди указанных методов наибольшей простотой обладают
оптические шар-пилотные наблюдения,
суть которых состоит в наблюдении с помощью аэрологического теодолита за перемещением в горизонтальной и вертикальной плоскостях оболочки, наполненной газом легче воздуха и свободно увлекаемой воздушным потоком.

Оптические однопунктные
шар-пилотные
измерения
скорости и направления ветра в свободной атмосфере

Для организации оптических однопунктные
шар-пилотных измерений
скорости и направления ветра в свободной атмосфере необходимо:
1. Латексная оболочка.
2. Комплект аппаратуры для наполнения оболочки: баллон с водородом, редуктор и шланг для подачи водорода в оболочку, грузики для определения свободной подъемной силы оболочки, весы для взвешивания оболочки перед наполнением ее водородом.
3. Аэрологический теодолит, секундомер.
4. Бланки для записи данных наблюдений.
5. Два наблюдателя.
5. Аппаратура и специализированные таблицы для обработки данных наблюдений.

Аэрологическая оболочка
Для однопунктных и базисных шар-пилотных наблюдений используются латексные оболочки № 10, 20 и 30 (цифры указывают диаметр оболочки в ненадутом состоянии в см)

Водородонаполнительное помещение

Процесс наполнения водородом латексной оболочки
Грузик для определения свободной подъемной силы

Секундомер механический СОСпр-2а
Секундомер электронный
Casio HS-80TW-1E
Весы электронные

Определение угловых координат шар-пилота с помощью аэрологического теодолита в полевых условиях

Офицерская школа морской авиации
(Баку, 1915 г.)

Аэрологические теодолиты

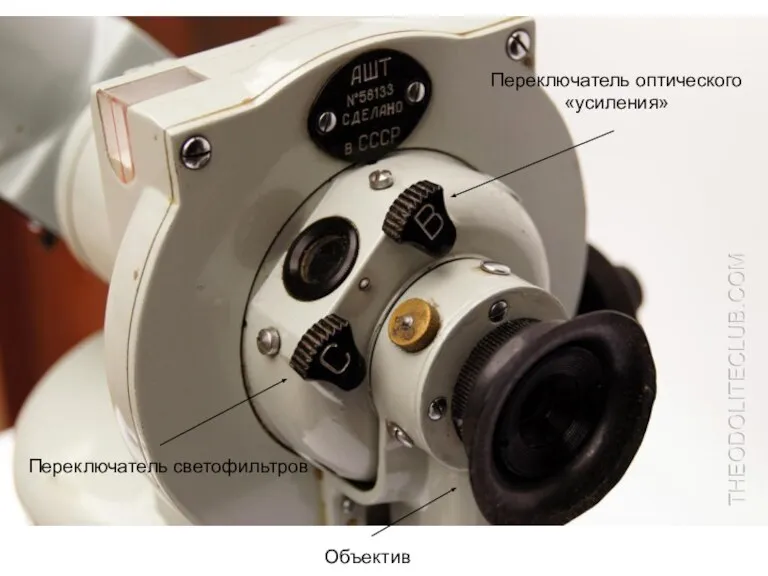
Аэрологический теодолит для определения угловых координат шар-пилота:
АШТ – аэрологический шар-пилотный теодолит

Переключатель светофильтров
Переключатель оптического «усиления»
Объектив

Уровень
Буссоль
Объектив
Окуляр
Винты для горизонтирования теодалита
Винты для смещения объектива при слежении за шар-пилотом
Стопорный винт для фиксации горизонтальной шкалы после ее установки на ноль с использованием буссоли

Установка теодолита.
Теодолит устанавливается либо на треноге, либо на специальном стационарном постаменте, имеющем тот же винт крепления, что и тренога.
Место размещения аэрологического теодолита должно находиться вдали от высоких предметов и обеспечивать подход к теодолиту со всех сторон.

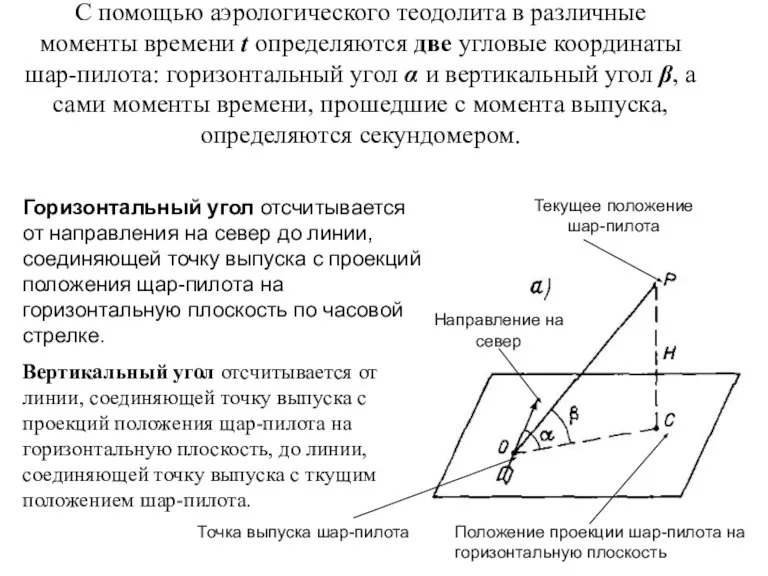
С помощью аэрологического теодолита в различные моменты времени t определяются две угловые координаты шар-пилота: горизонтальный угол α и вертикальный угол β, а сами моменты времени, прошедшие с момента выпуска, определяются секундомером.
Горизонтальный угол отсчитывается от направления на север до линии, соединяющей точку выпуска с проекций положения щар-пилота на горизонтальную плоскость по часовой стрелке.
Вертикальный угол отсчитывается от линии, соединяющей точку выпуска с проекций положения щар-пилота на горизонтальную плоскость, до линии, соединяющей точку выпуска с ткущим положением шар-пилота.
Текущее положение шар-пилота
Точка выпуска шар-пилота
Положение проекции шар-пилота на горизонтальную плоскость
Направление на север

Дискретность обрабатываемых моментов времени:
- через 0.5 мин с момента выпуска до 3-ей минуты включительно; - через 1 мин с 3-ей до 10-й мин; - через 2 мин с 10-й мин до 40 мин,
- через 4 мин с 40 мин до конца подъёма, включая последнюю минуту наблюдения.
Для контроля данные о вертикальных углах записываются в таблицу наблюдений после третьей минуты каждую минуту.

Погрешности шар-пилотных наблюдений
Инструментальные погрешности

Ошибки, возникающие при установке и настройке теодолита:
Ошибка, вызванная смещением нуля вертикального круга.
Ошибка, вызванная наличием угла коллимации.
Ошибка, связанная с неправильным горизонтированием теодолита.
Ошибка, связанная с неправильной ориентацией теодолита относительно географических координат.

Ошибка, вызванная смещением нуля вертикального круга: Δα.
Для определения величины ошибки смещением нуля вертикального круга теодолит наводят на удаленный предмет и определяют вертикальный угол α1. Затем переводят труду через зенит и снова наводят на тот же предмет и определяют второй вертикальный угол α2. Поскольку
α1 = αист + Δα, а α2 = αист + 1800 - Δα .
Подставляя из первого уравнения αист во второе уравнение, получаем
α2 = α1 – Δα + 1800 – Δα = α1 + 1800 – 2 Δα
или
α2 = α1 + 1800 – 2 Δα.
Решая последнее уравнение относительно Δα, получаем
Δα = (α1 – α2 – 1800) / 2.
После проведения измерений для получения правильного значения вертикального угла к измеренным значениям необходимо вводить поправку Δα (с соответствующим знаком), если измеренная при юстировки теодолита величина Δα > 0.20.

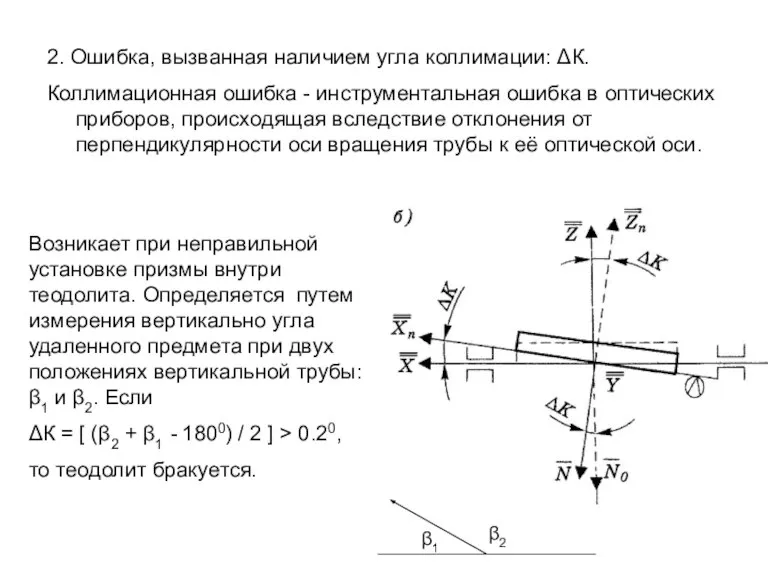
2. Ошибка, вызванная наличием угла коллимации: ΔК.
Коллимационная ошибка - инструментальная ошибка в оптических приборов, происходящая вследствие отклонения от перпендикулярности оси вращения трубы к её оптической оси.
Возникает при неправильной установке призмы внутри теодолита. Определяется путем измерения вертикально угла удаленного предмета при двух положениях вертикальной трубы: β1 и β2. Если
ΔК = [ (β2 + β1 - 1800) / 2 ] > 0.20,
то теодолит бракуется.
β1
β2

3. Ошибка, связанная с неправильным горизонтированием теодолита.
Устраняется путем устойчивого закрепления треноги теодолита на грунте (если не используются специальные бетонные постаменты) и подстройки положения теодолита на треноге за счет вращения трех регулировочных винтов.
Регулировка продолжается до тех пор, пока при любом положении теодолита после его вращения вокруг вертикальной оси воздушный пузырек уровня остается точно по середине шкалы.

4. Ошибка, связанная с неправильной ориентацией теодолита относительно географических координат.
Данный вид ошибки возникает при ориентации теодолита по буссоли без учета магнитного склонения пункта его размещения.
Магнитное склонение — угол между географическим и магнитным меридианами в точке земной поверхности. Магнитное склонение считается положительным, если северный конец магнитной стрелки компаса отклонен к востоку от географического меридиана, и отрицательным — если к западу.
При восточном магнитном склонении при юстировки теодолита к 00 горизонтальной шкалы прибавляется величина магнитного склонения, при западном – вычитается.
Для СПб (300 Е и 600 N) магнитное склонение равно +10.90 Е и изменяется на 0.140 в год к Е.
Для определения величины магнитного склонения для различных географических пунктов существуют соответствующие справочники, карты и «калькуляторы» в Интернете.

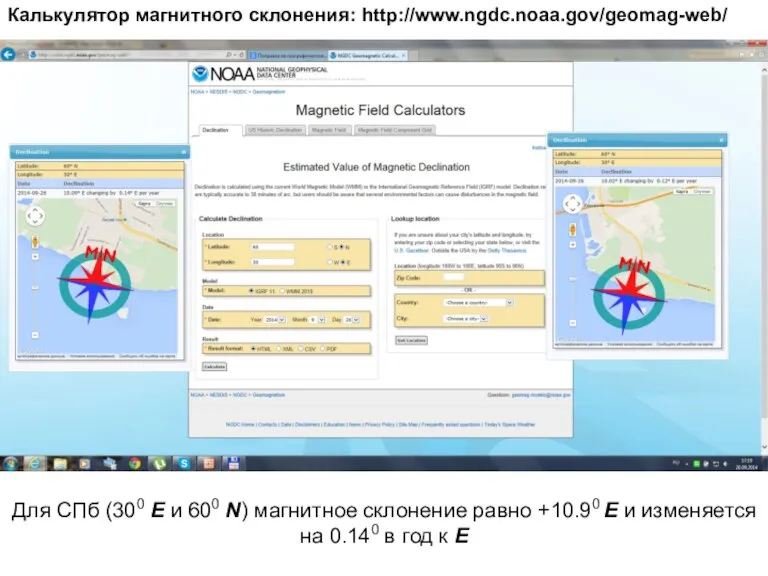
Калькулятор магнитного склонения: http://www.ngdc.noaa.gov/geomag-web/
Для СПб (300 Е и 600 N) магнитное склонение равно +10.90 Е и изменяется на 0.140 в год к Е

При многократном проведении измерений из одного и того же места для точной ориентации теодолита можно использовать первый способ: меру – видимый из места установки предмет, азимут которого заранее известен. После наведения теодолита на меру устанавливают известное значение азимута и закрепляют горизонтальную шкалу стопорным винтом.
Второй способ ориентации без использования буссоли – ориентация по полярной звезде, азимут которой равен 00.
Третий способ – ориентация по Солнцу: в истинный полдень тень от теодолита проходит точно по меридиану. Правда, для этого необходимо знать не московское, а истинное солнечное время.

Определение вертикальной скорости шар-пилота

Поскольку мы живем в трехмерном мире, то для определения положения любой точки в пространстве необходимы три координаты.
Оптический метод пеленгации с помощью аэрологического теодолита позволяет измерить только две координаты (α и β ) из трех, необходимых для:
1) задания положений шар-пилота в пространстве в разные моменты времени;
2) определения координат проекций шар-пилота на горизонтальной плоскости;
3) определения длины отрезков прямых, соединяющих эти проекций;
4) определения ориентации отрезков прямых, соединяющих эти проекций, относительно направления на север.

Недостающая третья координата – высота H, рассчитывается по вертикальной скорости подъемы шар-пилота w, которая определяется до его запуска.
При этом предполагается, что вертикальная скорость подъемы шар-пилота остается постоянной за все время наблюдения, что не в полной мере соответствует действительности и вносит методическую погрешность в определение скорости и направления ветра.

Следовательно, существенным фактором, определяющим возможность реализации оптического однопунктного шар-пилотного метода ветровых измерений в атмосфере, является возможность предварительного (до запуска шар-пилота в атмосферу) определения его вертикальной скорости движения.
Для решения этой задачи рассмотрим особенности движения шара в вертикальной плоскости.

Эластичная оболочка шара-пилота после наполнения ее газом приобретает сферическую форму. При этом давление газа внутри оболочки лишь незначительно превышает давление окружающего воздуха.
На основании закона Архимеда наполненная газом легче воздуха оболочка будет под воздействие выталкивающей силы двигаться вверх.
В предположении, что оболочка невесома, такая выталкивающая сила, называемая полной подъемной силой E, будет равна
где V — объем оболочки шара-пилота; g — ускорение силы тяжести; ρВ и ρГ — плотности воздуха и газа соответственно. При 00С и давлении 1023 гПа ρВ - ρГ ≈ 1.2 кг/м3 (для технического водорода).
При радиусе наполненной водородом оболочки в 30 см ее полная подъемная сила будет составлять около 135 г.

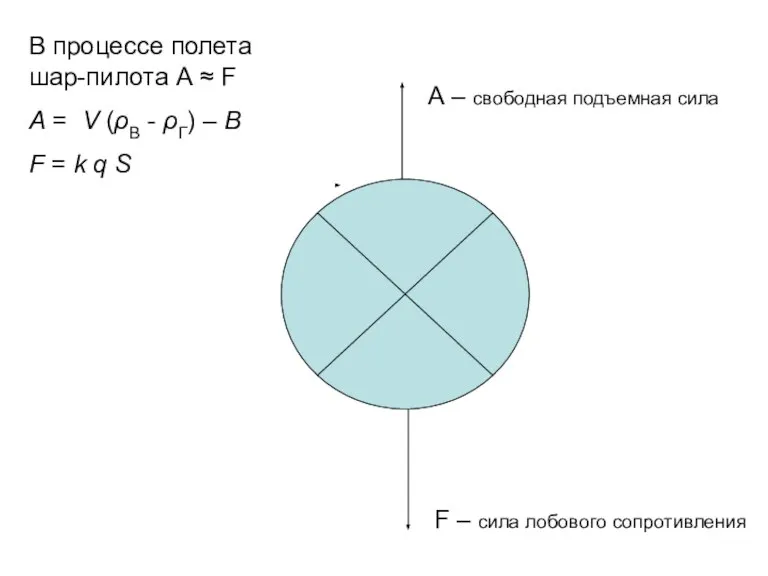
Так как оболочка имеет вес В, то свободная подъемная сила А, действующая на неё вверх, будет равна:
А = Е – В = V (ρВ - ρГ) – В.
Свободная подъемная сила оболочки определяется во время ее наполнения водородом по величине поднимаемого грузика и, следовательно, известна.
Второй силой, которая будет действовать на оболочку и которая будет направлена вниз, является сила лобового сопротивления F, величина которой определяется следующим соотношением:
F = k q S,
где k — коэффициент лобового сопротивления, зависящий от формы оболочки и режима обтекания шара воздушным потоком,
q — динамическое давление, испытываемое шаром со стороны обтекающего потока, S — площадь поперечного сечения шара.

В процессе полета шар-пилота А ≈ F
А = V (ρВ - ρГ) – В
F = k q S
А – свободная подъемная сила
F – сила лобового сопротивления

В случае, если оболочка имеет сферическую форму,
S = π D2 /4 и q = ρВ w2 / 2,
где D — диаметр шара, w – вертикальная скорость движения шар-пилота.
Теперь выражение для F можно записать в виде:
F = k q S,

Эксперименты показали, что практически сразу же после выпуска шар поднимается равномерно, т.е. происходит установившееся движение, при котором обе силы уравновешиваются и, следовательно, A = F. Подставляя в последнем уравнении F вместо А, получаем:
Разрешая последнее выражение относительно w, получаем
Для расчета w по этой формуле необходимо знать коэффициент лобового сопротивления оболочки k, плотность воздуха ρ, свободную подъемную силу оболочки А и ее диаметр D.

Более удобной для расчета вертикальной скорости шара-пилота W(м/мин ) является следующая формула
где С - коэффициент, зависящий от грузоподъемности (свободной подъемной силы) оболочки A; B - вес оболочки; рO - давление на уровне моря по стандартной атмосфере; р и t – атмосферное давление и температура воздуха у поверхности Земли в момент выпуска шара-пилота.

Напомним, что:
свободная подъемная сила шара-пилота А измеряется в процессе наполнения оболочки газом с помощью подвешенного к ней грузика,
вес оболочки В определяется путем взвешивания оболочки до ее наполнения водородом.

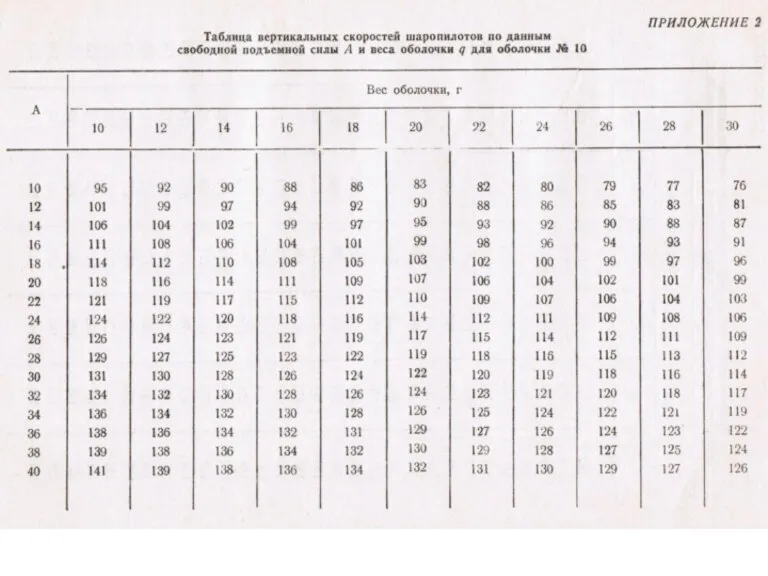
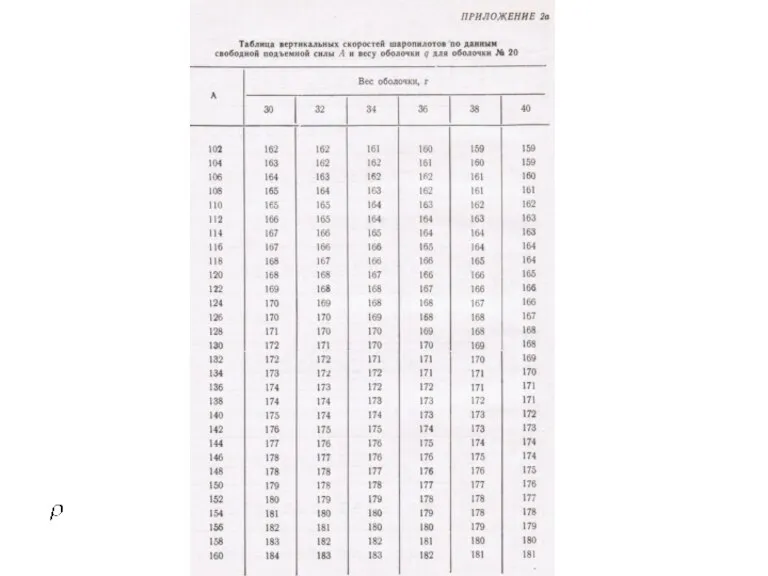
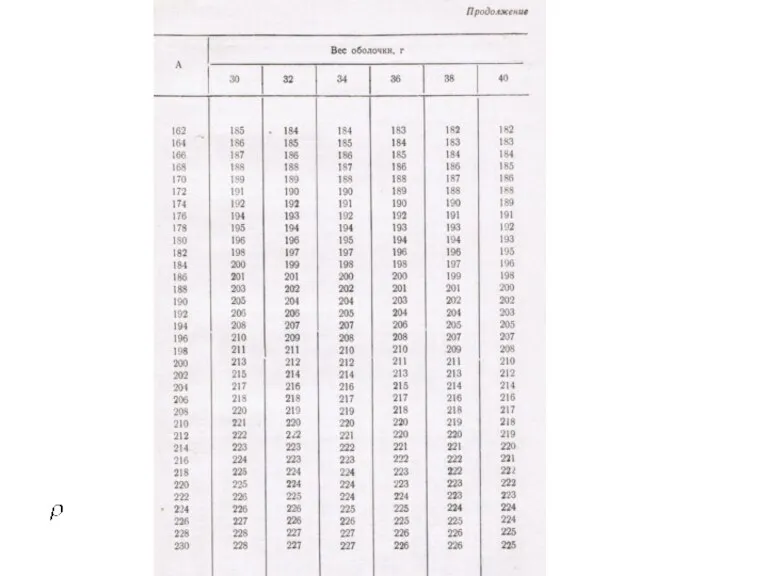
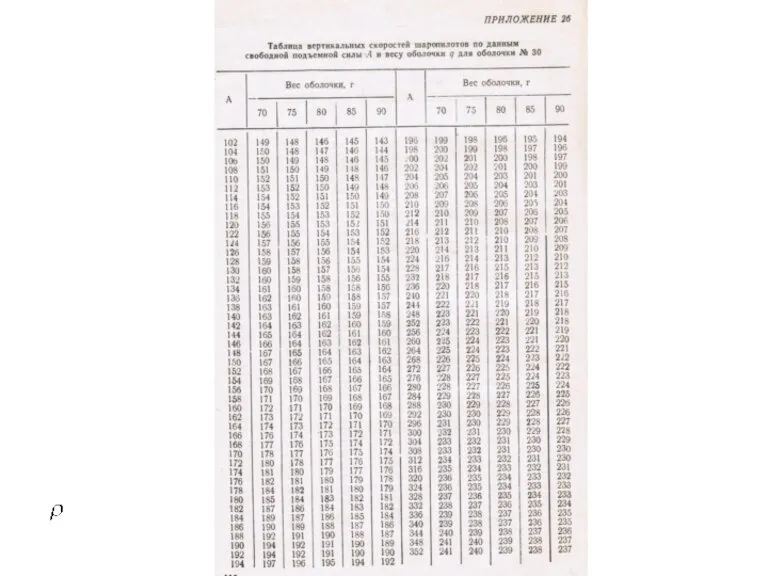
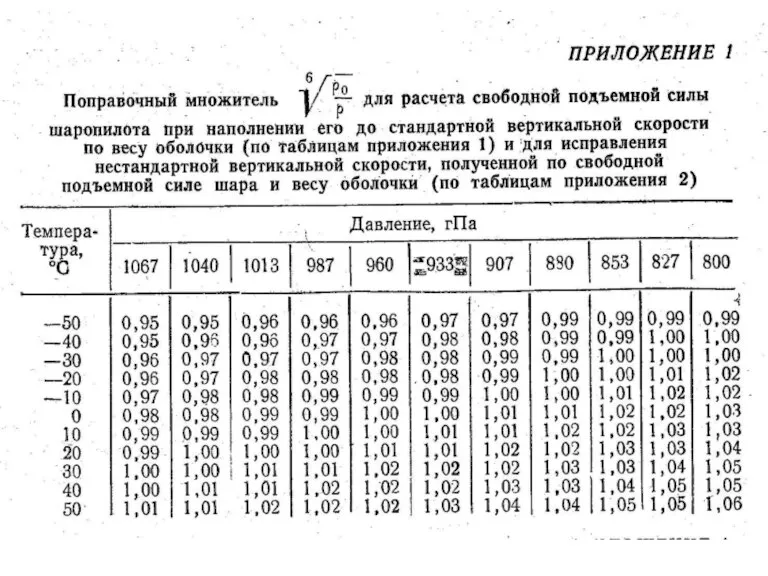
На практике при проведении однопунктных шар-пилотных наблюдений для расчета вертикальной скорости подъема w используются специальные таблицы, приведенные в «Практикуме по аэрологи». Определение величины w производится в два этапа:
Сначала по таблицам приложения 2 «Практикуме по аэрологи» определяется не исправленная на текущую плотность воздуха величина w0.
Затем по таблице в приложении 1 «Практикуме по аэрологи» определяют поправочный множитель, учитывающий отличие текущих условий от стандартных. После перемножения w0 на поправочный множитель получают искомую вертикальную скорость подъема шар-пилота w.

Погрешности шар-пилотных наблюдений
Методические погрешности

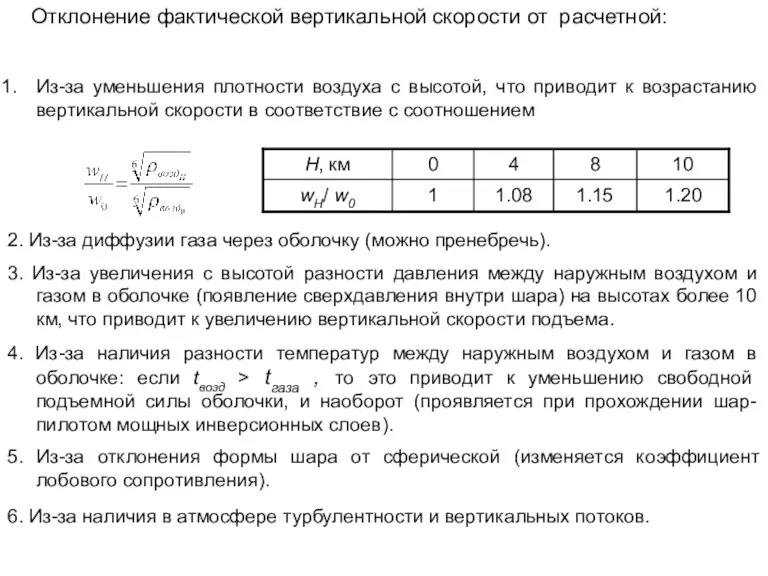
Отклонение фактической вертикальной скорости от расчетной:
Из-за уменьшения плотности воздуха с высотой, что приводит к возрастанию вертикальной скорости в соответствие с соотношением
2. Из-за диффузии газа через оболочку (можно пренебречь).
3. Из-за увеличения с высотой разности давления между наружным воздухом и газом в оболочке (появление сверхдавления внутри шара) на высотах более 10 км, что приводит к увеличению вертикальной скорости подъема.
4. Из-за наличия разности температур между наружным воздухом и газом в оболочке: если tвозд > tгаза , то это приводит к уменьшению свободной подъемной силы оболочки, и наоборот (проявляется при прохождении шар-пилотом мощных инверсионных слоев).
5. Из-за отклонения формы шара от сферической (изменяется коэффициент лобового сопротивления).
6. Из-за наличия в атмосфере турбулентности и вертикальных потоков.

Методика определения вертикального профиля скорости и направления ветра

Основные предположения:
1. Шар-пилот полностью увлекается воздушным горизонтальным потоком.
2. Вертикальная скорость подъема шар-пилота может быть определена на основе измерения веса оболочки и ее свободной подъемной силы.
3. Вертикальная скорость подъема шар-пилота не меняется с высотой.

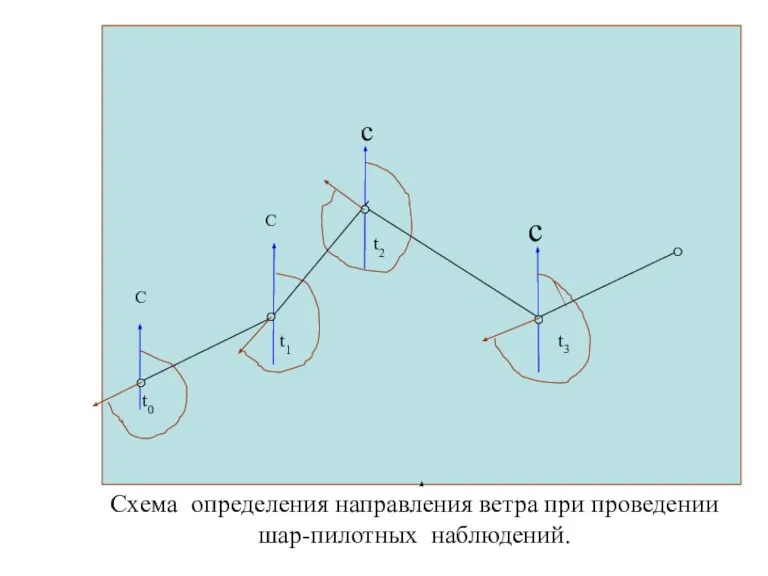
Схема однопунктных шар-пилотных наблюдений
Р1, Р2, Р3 – положение шар-пилота в моменты времени t1, t2,t3;
С1, С2, С3 – положение проекций шар-пилота на горизонтальную плоскость;
H1, H2,H3 – высота подъёма шар-пилота;
угол α - азимут (горизонтальный), угол β - вертикальный

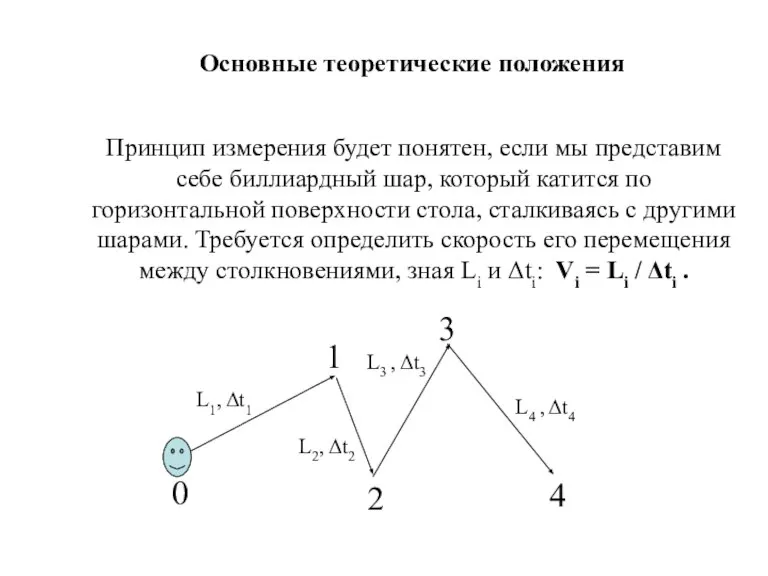
Основные теоретические положения
Принцип измерения будет понятен, если мы представим себе биллиардный шар, который катится по горизонтальной поверхности стола, сталкиваясь с другими шарами. Требуется определить скорость его перемещения между столкновениями, зная Li и Δti: Vi = Li / Δti .
0
1
2
3
4
L1, Δt1
L2, Δt2
L3 , Δt3
L4 , Δt4

Направление ветра отсчитывается:
от направления на север;
по часовой стрелки;
до вектора, который указывает откуда дует ветер.

Схема определения направления ветра при проведении шар-пилотных наблюдений.
С
С
с
с
t0
t1
t2
t3

Подготовка к обработке данных шар-пилотных наблюдений:
1. Расчет вертикальной скорости подъема шар-пилота w.
2. Расчет высоты подъема шар-пилота H.

Расчет высоты шар-пилота
Высоту H можно определить, если известны вертикальная скорость шар-пилота w и время Δt, прошедшее с момента выпуска шар-пилота:
H = w • Δt .
Вертикальная скорость шар-пилота определяется перед выпуском шар-пилота, а время – по секундомеру.
Практически определение вертикальной скорости шар-пилота значительно упрощается с помощью специальных таблиц, учитывающие еще и поправки на изменение плотности воздуха с изменением температуры.

Дискретность обработки данных шар-пилотных наблюдений
Дискретность обрабатываемых моментов времени:
через 0.5 мин до 3-ей минуты включительно;
через 1 мин с 3-ей до 10-й мин;
через 2 мин с 10-й мин до 40 мин,
- через 4 мин с 40 мин до конца подъёма, включая последнюю минуту наблюдения.

Особенность использования метода оптических шар-пилотных наблюдений заключается в том, что с его помощью могут быть рассчитаны лишь осредненная в слоях атмосферы скорость и направление ветра.
Толщина каждого такого слоя определяется вертикальной скоростью перемещения объекта и интервалами времени между смежными отчетами.
В дальнейшем эти значения рассматриваются как скорость и направления ветра на высотах, соответствующие высоте середины соответствующих слоев.

Существуют графический и аналитический методы обработки данных шаропилотных наблюдений.
Первоначально наибольшее развитие в оперативной практике получил графический метод, который обладает достаточной простотой и наглядностью. Однако графический метод не обеспечивает достаточной точности обработки исходных данных, поскольку при реализации графического метода часто возникают ошибки как субъективного, так и методического характера.

От указанных недостатков графического метода свободен аналитический метод обработки данных шаропилотных наблюдений.
Учитывая преимущества и недостатки этих двух методов рассмотрим последовательно их реализацию.

Графический метод

Графический метод обработки данных однопунктных шар-пилотных наблюдений состоит из двух этапов.
Этап 1. Построение положений проекций шар-пилота на горизонтальной поверхность в разные моменты времени.
Этап 2. Последовательное использование положений двух соседних пар проекций для определения скорости и направления ветра.

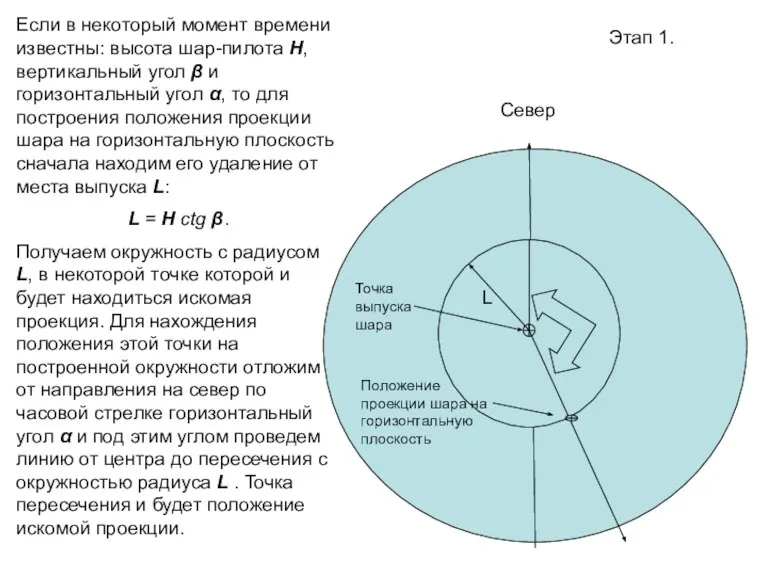
Этап 1.
Север
Если в некоторый момент времени известны: высота шар-пилота H, вертикальный угол β и горизонтальный угол α, то для построения положения проекции шара на горизонтальную плоскость сначала находим его удаление от места выпуска L:
L = H ctg β.
Получаем окружность с радиусом L, в некоторой точке которой и будет находиться искомая проекция. Для нахождения положения этой точки на построенной окружности отложим от направления на север по часовой стрелке горизонтальный угол α и под этим углом проведем линию от центра до пересечения с окружностью радиуса L . Точка пересечения и будет положение искомой проекции.
L
Точка выпуска шара
Положение проекции шара на горизонтальную плоскость

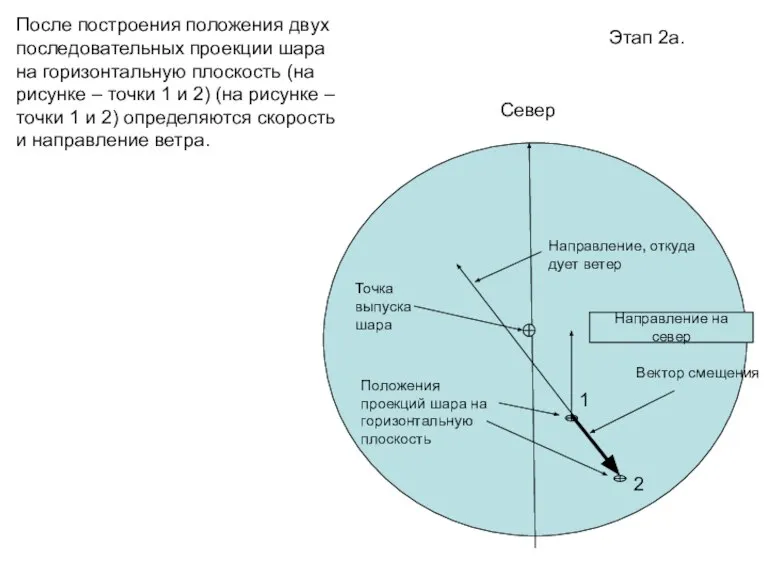
Этап 2а.
Север
После построения положения двух последовательных проекции шара на горизонтальную плоскость (на рисунке – точки 1 и 2) (на рисунке – точки 1 и 2) определяются скорость и направление ветра.
Точка выпуска шара
Положения проекций шара на горизонтальную плоскость
1
2
Вектор смещения
Направление, откуда дует ветер
Направление на север

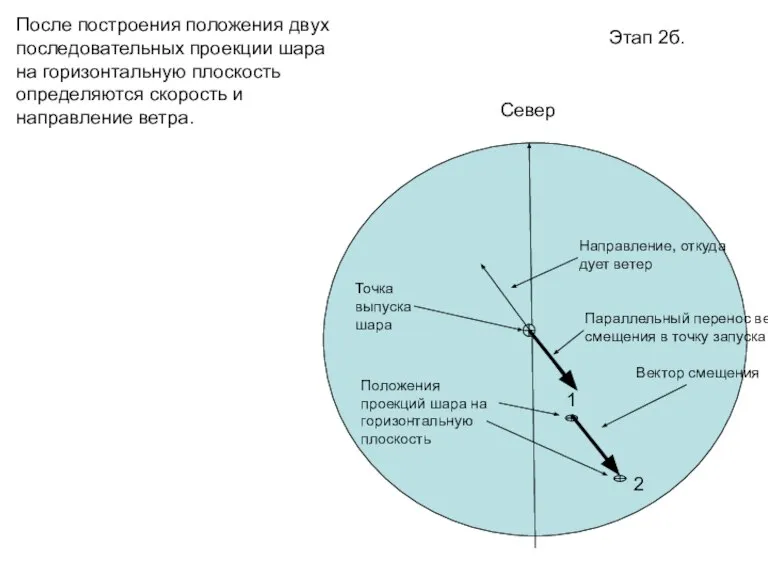
Этап 2б.
Север
После построения положения двух последовательных проекции шара на горизонтальную плоскость определяются скорость и направление ветра.
Точка выпуска шара
Положения проекций шара на горизонтальную плоскость
1
2
Вектор смещения
Направление, откуда дует ветер
Параллельный перенос вектора смещения в точку запуска

Для графического определения скорости и направления ветра на высотах по результатам шаропилотных наблюдений используется круг Молчанова (СИНОНИМ: аэрологический планшет А-30).
Этот прибор состоит из:
- металлического неподвижного диска, на одной из сторон которого отпечатана номограмма,
- прозрачного целлулоидного круга, который вращается около центра неподвижного круга,
- подвижной линейки, вращающейся вокруг центра круга.
На прозрачном круге с помощью номограммы строится горизонтальная проекция шара-пилота, по которой определяются скорость и направление ветра.

Внешний вид круга Молчанова (аэрологический планшет А-30).

Аналитический метод

Более точными, естественно, являются аналитические методы обработки, использование которых в оперативной практике возможно лишь при использовании компьютерной техники. Применение компьютерной техники в то же время позволяет архивировать исходные данные и результаты расчетов, упростить процесс представления информации и передачи ее потребителям, повысить культуру труда .

Алгоритм обработки данных однопунктных шар-пилотных наблюдений

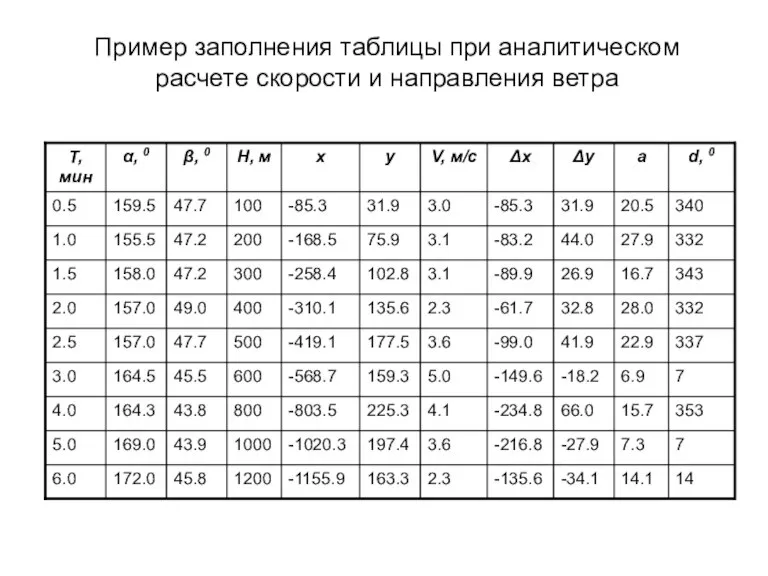
Пример заполнения таблицы при аналитическом расчете скорости и направления ветра

Пример обработки данных однопунктных шар-пилотных наблюдений
W=200 м/мин; H1=200 0.5 =100м; H2=200 1.0 =200м;
X1=100 ctg (47.7) cos (159.5) = 100 0.91 (-0.937) = -85.3
X2 = 200 ctg (47.2) cos (155.5) = 200 0.926 (-0.91) = -168.5
Y1 = 100 ctg (47.7) sin (159.5) = 100 0.91 0.35 = 31.9
y2 = 200 ctg (47.2) sin (155.5) = 200 0.926 0.41 = 75.9
V1,0 = [ (-85.3 - 0)2 + (31.9 - 0)2 ] / [60 (0.5 - 0)] = 3.0
V2,1 = [ (-168.5 + 85.3)2 + (75.9 – 31.9)2 ] / [60 (1 - 0.5)] = 3.1

A1,0 = arc tg I [(31.9 - 0) / (-85.3 - 0)] = 20.5; Δx <0; Δy>0
A2,1 = arc tg I [(75.9 – 31.9) / (-168.5 + 85.3)] = 27.9; Δx <0; Δy>0
D1,0 = 360 – 20.5 = 239.5
D2,1 = 360 – 27.9 = 232.1

Представление данных однопунктных шар-пилотных наблюдений

Полученные значения скорости и направления ветра, отнесенные к высотам середины слоев над уровнем моря, наносят на график, который строится в масштабе: по вертикали - 1 см ~ 1 км; по горизонтали - 1 см ~ 2м/c, 1 см ~ 100. Первой точкой на графиках наносится данные о скорости и направлении ветра на уровне станции.
В слое до 3-х км строят дополнительный график зависимости направления ветра от высоты в масштабе по вертикали 1 см - 200 м,
по горизонтали 1 см – 100.
Все нанесенные точки соединяют прямыми линиями (кусочно-линейная интерполяция).

Полученные значения скорости и направления ветра записывают в соответствующие графы бланка КАЭ-3 в строку, соответствующую концу обрабатываемого интервала времени, т.е. моменту времени ti.
Осуществляют привязку полученных ветровых характеристик к высоте. При этом найденные значения скорости и направления ветра относят к высоте середины слоя, пройденному радиозондом за соответствующий интервал времени.

Высота середины слоя определяется по построенному графику H(t) для момента времени, равному среднему значению из двух соседних обрабатываемых моментов времени.
Найденные значения высот записывают в графу “Высота середины слоя над уровнем моря” бланка КАЭ-3, графу “Высота середины слоя над поверхностью земли” заполняется до высоты 1000 м, вычитая из высоты середины слоя над уровнем моря высоту станции.
Расчет скорости и направления ветра для стандартных уровней производится по стандартным формулам линейной интерполяции.

С построенных графиков снимают значения скорости и направления ветра на стандартных высотах, изобарических поверхностях, высотах особых точек, уровнях наибольшей скорости ветра и максимальной скорости ветра.

В основу критерия для выбора особых точек ветра положена возможность восстановления по этим точкам кривой изменения с высотой направленияветра с точностью до 100, скорости ветра до 5 м/с.
Особыми точками ветра являются начальная и конечная высота подъема, уровень максимальной скорости ветра, границы пропуска в наблюдениях. Уровнем максимального ветра считается слой атмосферы выше изобарической поверхности 500 гПа (5500 м) где наблюдается скорость ветра превышающая 30 м/с и изменение скорости в двух километровом слое выше или ниже больше 10 м/с.

Дополнительно на построенных кривых изменения ветра с высотой намечают предполагаемые особые точки, где наблюдается значительный излом кривых.
Затем последовательно, в порядке возрастания высоты, исследуют каждую предполагаемую особую точку. Для этого соединяют прямой две соседние с исследуемой точки: нижележащую, уже выбранную особую точку, и вышележащую предполагаемую особую точку. На этой прямой на уровне исследуемой точки определяют линейно интерполированное значение скорости или направления ветра.

Исследуемую точку включают в число особых, если:
линейно интерполированное значение скорости ветра отличается от действительного более чем на 5 м/c;
линейно интерполированное значение направления ветра отличается от действительного более чем на 100.
Найденные значения скорости и направления ветра на стандартных высотах, стандартных изобарических поверхностях, высотах особых точек записывают в соответствующие графы бланка КАЭ-3а с точностью до целых.

Оптические базисные
шар-пилотные
измерения
скорости и направления ветра в свободной атмосфере

Главное отличие базисных от однопунктных наблюдений состоит в том, что при проведении базисных высоты подъем шар-пилота рассчитывается на основе теодолитных измерений, а не по вертикальной скорости его подъема.
Это достигается тригонометрическим расчетом высоты шар-пилота на основе проведения одновременных наблюдений с помощью двух оптических теодолитов, расположенных на известном расстоянии друг от друга.

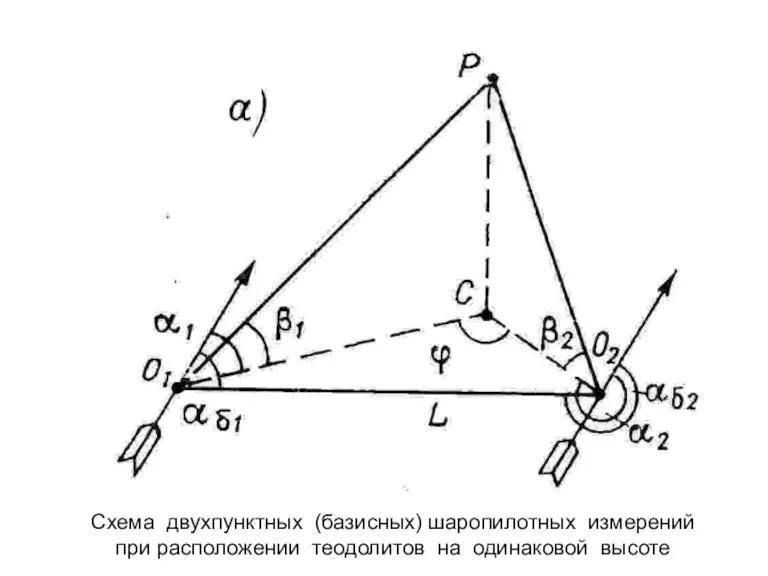
Схема двухпунктных (базисных) шаропилотных измерений при расположении теодолитов на одинаковой высоте

В данном методе расстояние между теодолитами (длина базы L) и углы (αБ1 и αБ2) для данной базы являются величинами постоянными и измеряются заранее.
Для каждого момента времени t с помощью аэрологических теодолитов из точек O1 и O2 производится измерение вертикальных углов: β1 и β2, и горизонтальных углов: α1 и α2.
Наличие двух горизонтальных углов: α1 и α2, и углов αБ1 и αБ2 позволяет полностью решить треугольник O1CO2 , так как известна одна из его сторон (сторона L) и все три угла:
Если α2 > αБ2 и α1 < αБ1, то используется знак “плюс”; в остальных случаях - знак “минус”.

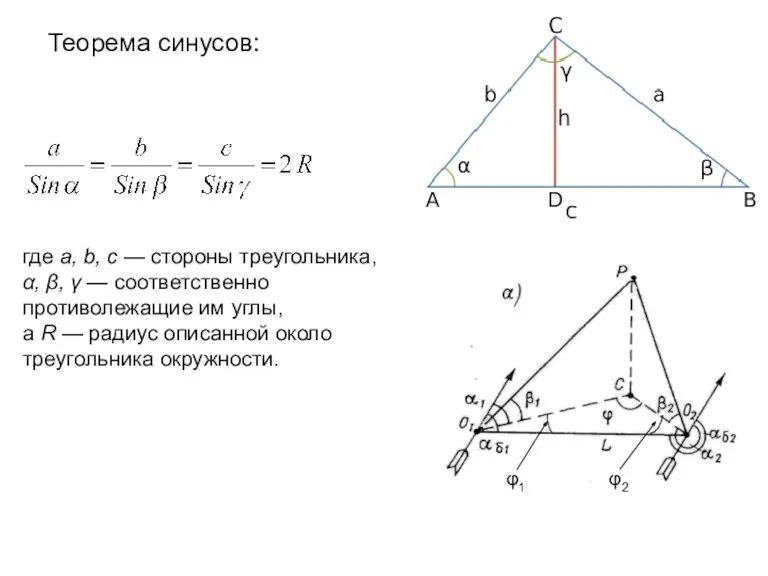
где a, b, c — стороны треугольника,
α, β, γ — соответственно
противолежащие им углы,
а R — радиус описанной около треугольника окружности.
Теорема синусов:
φ1
φ2

Для каждого момента времени t с помощью аэрологических теодолитов из точек O1 и O2 производится измерение горизонтальных углов α1 и α2. Таким образом, треугольник O1CO2 оказывается полностью заданным, так как известна одна из его сторон (сторона L) и все три угла.
Для треугольника O1CO2 , используя теорему синусов, можно записать (см. рис.):
Откуда:
.

Зная сторону СО1 прямоугольного треугольника О1СР можно определить высоту шар-пилота в разные моменты времени
Таким образом, для определения высоты шар-пилота в различные моменты времени не требуется задания вертикальной скорости его подъема – высота рассчитывается по данным угловых измерений от двух теодолитов, расположенных на известном расстоянии друг от друга. Затем скорость и направление ветра определяется аналогично методу однопунктных наблюдений.

На практике для проведения базисных шар-пилотных наблюдений готовят две базы, расположенные приблизительно перпендикулярно друг другу.
Из этих двух баз для проведения конкретного наблюдения выбирают ту, которая расположена перпендикулярно предполагаемому движению шар-пилота.
Это связано с тем, что в случае перемещения проекций шар-пилота точно параллельно базе из тригонометрических расчетов нельзя будет определить высоты, на которых будет находиться шар-пилот.

Какие будут вопросы?