Содержание
- 2. Funcţii continue pe spaţii topologice
- 3. Dacă X şi Y sunt două spaţii topologice şi f:X→Y este o funcţie, atunci următoarele afirmaţii
- 4. Topologie
- 5. Mulţimi deschise/închise
- 6. Tipuri de topologii
- 7. Vecinătăți
- 8. Puncte Frontieră Exterior Se numeşte exteriorul mulţimii A, şi se notează cu exterior(A), mulţimea int(X-A). Un
- 9. Homeomorfism
- 11. Скачать презентацию








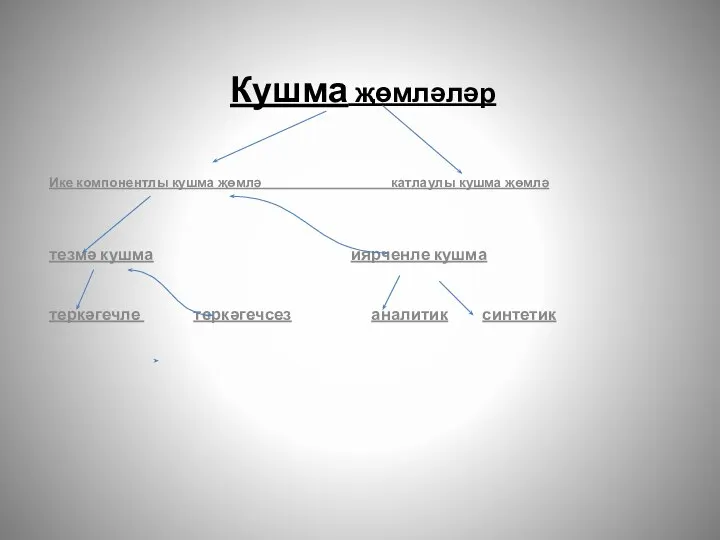 Кушма җөмләләр
Кушма җөмләләр Крым
Крым Классификация и типология современных ландшафтных объектов
Классификация и типология современных ландшафтных объектов My hometown is Kostanay
My hometown is Kostanay Влажность воздуха. Способы определения влажности воздуха
Влажность воздуха. Способы определения влажности воздуха Презентация на тему Население России (8 класс)
Презентация на тему Население России (8 класс)  Край ты мой родной. Урок-путешествие
Край ты мой родной. Урок-путешествие Реки Красноярского края - презентация к уроку Географии_
Реки Красноярского края - презентация к уроку Географии_ Что у нас под ногами. Состав почвы
Что у нас под ногами. Состав почвы Кругообіг води в природі
Кругообіг води в природі Наземная инфраструктура ГЛОНАСС-GPS Новосибирской области
Наземная инфраструктура ГЛОНАСС-GPS Новосибирской области Население Оренбургской области. Национальный состав
Население Оренбургской области. Национальный состав Миграции населения России
Миграции населения России Океаны и моря
Океаны и моря Презентация на тему Волгоград
Презентация на тему Волгоград  Шарканский район
Шарканский район Три теории происхождения нефти
Три теории происхождения нефти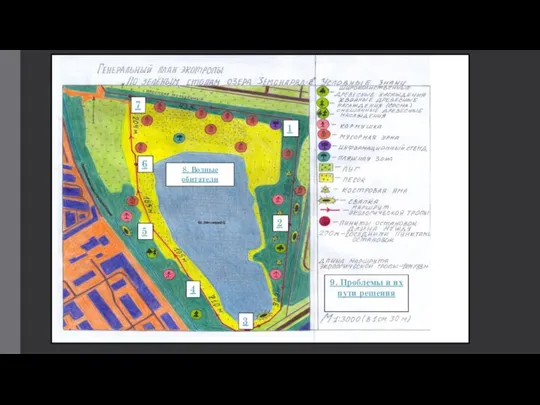 Генеральный план экотропы
Генеральный план экотропы 20161219_klimat1
20161219_klimat1 Республика Бурятия
Республика Бурятия 20180128_dalniy_vostok_moya
20180128_dalniy_vostok_moya Географическое положение города Коломны
Географическое положение города Коломны 20140317_klimat_evrazii
20140317_klimat_evrazii Libya - the Arab state in North Africa
Libya - the Arab state in North Africa Театры Санкт-Петербурга
Театры Санкт-Петербурга Виртуальная экскурсия по Чаплыгину
Виртуальная экскурсия по Чаплыгину Здравницы Крыма
Здравницы Крыма Республика Хорватия
Республика Хорватия