Ориентирование линий. Прямая и обратная геодезические задачи

ОРИЕНТИРОВАНИЕ ЛИНИЙ
Ориентировать линию – значит, определить её положение относительно известного, или исходного направления
Известные направления – те направления, которые были определены ранее
Исходные направления – северные направления трёх меридианов:
Географического (истинного)
Магнитного
Осевого

ОБОЗНАЧЕНИЕ ИСХОДНЫХ НАПРАВЛЕНИЙ
Ориентирующий угол – угол, отсчитываемый по ходу часовой стрелки (вправо) от исходного направления до ориентируемой линии
Существует три вида ориентирующих углов:
Географический азимут (истинный азимут) Аг (Аи) (Г)
Магнитный азимут Ам (М)
Дирекционный угол α
Происхождение терминов:
А́зимут от араб. السموت‎, (ас-сумут, направление
Дирекционный угол (от англ. Direction) - направление

СБЛИЖЕНИЕ МЕРИДИАНОВ

ОСНОВЫ ТЕОРИИ ЗЕМНОГО МАГНЕТИЗМА
Собственное магнитное поле Земли можно разделить на три составляющие:
главное поле,
поля мировых аномалий,
внешнее магнитное поле.

ГЛАВНОЕ ПОЛЕ
Более чем на 90 % оно состоит из поля, источник которого находится внутри Земли, в жидком внешнем ядре, — эта часть называется главным, основным или нормальным полем. Оно аппроксимируется в виде ряда по гармоникам — ряда Гаусса, а в первом приближении вблизи поверхности Земли (до трёх её радиусов) близко к полю магнитного диполя, то есть имеет такой вид, как будто земной шар представляет собой полосовой магнит с осью, направленной приблизительно с севера на юг. Центр этого диполя смещён относительно центра Земли, а ось наклонена к оси вращения Земли на угол около 10°. На такой же угол отстоят от соответствующих географических полюсов геомагнитные полюса — точки пересечения оси диполя с поверхностью Земли. Их положение в различные моменты времени вычисляется в рамках той или иной модели магнитного поля, определяющей тем или иным образом первые три коэффициента в ряду Гаусса. Эти глобальные модели — такие как Международное геомагнитное аналитическое поле (International Geomagnetic Reference Field, IGRF) и Всемирная магнитная модель (World Magnetic Model, WMM) — создаются различными международными геофизическими организациями, и каждые 5 лет утверждаются и публикуются обновлённые наборы коэффициентов Гаусса, определяющих все данные о состоянии геомагнитного поля и его параметрах. Так, согласно модели WMM2015, северный геомагнитный полюс (по сути это южный полюс магнита) имеет координаты 80,37° с. ш. и 72,62° з. д., южный геомагнитный полюс — 80,37° ю. ш., 107,38° в. д., наклон оси диполя относительно оси вращения Земли — 9,63°

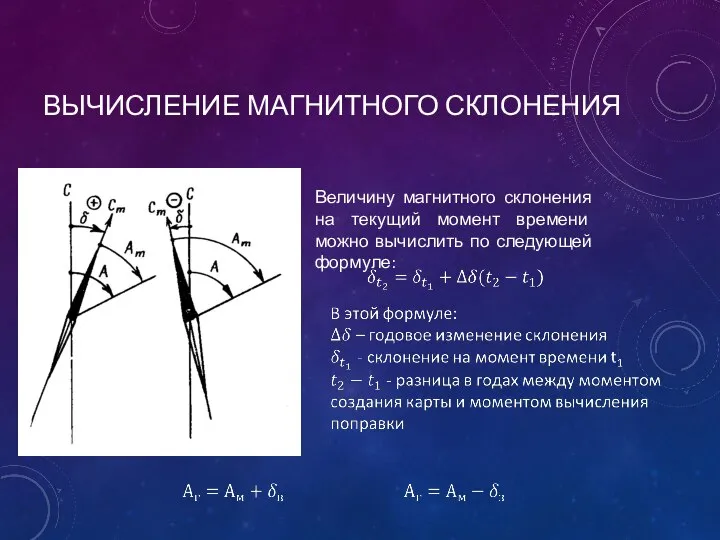
ПОЛЯ МИРОВЫХ АНОМАЛИЙ
Реальные силовые линии магнитного поля Земли, хотя в среднем и близки к силовым линиям диполя, отличаются от них местными нерегулярностями, связанными с наличием намагниченных пород в коре, расположенных близко к поверхности. Из-за этого в некоторых местах на земной поверхности параметры поля сильно отличаются от значений в близлежащих районах, образуя так называемые магнитные аномалии. Они могут накладываться одна на другую, если вызывающие их намагниченные тела залегают на разных глубинах.
Существование магнитных полей протяжённых локальных областей внешних оболочек приводит к тому, что истинные магнитные полюса — точки (вернее, небольшие области), в которых силовые линии магнитного поля абсолютно вертикальны, — не совпадают с геомагнитными, при этом они лежат не на самой поверхности Земли, а под ней. Координаты магнитных полюсов на тот или иной момент времени также вычисляются в рамках различных моделей геомагнитного поля путём нахождения итеративным методом всех коэффициентов в ряду Гаусса. Так, согласно актуальной модели WMM, в 2015 г. северный магнитный полюс находился в точке 86° с. ш., 159° з. д., а южный — 64° ю. ш., 137° в.д. Значения актуальной модели IGRF12 немного отличаются: 86,3° с. ш., 160° з. д., для северного полюса, 64,3° ю. ш., 136,6° в.д для южного
Соответственно, магнитная ось — прямая, проходящая через магнитные полюса, — не проходит через центр Земли и не является её диаметром.
Положения всех полюсов постоянно смещаются — геомагнитный полюс прецессирует относительно географического с периодом около 1200 лет

ВНЕШНЕЕ МАГНИТНОЕ ПОЛЕ
Оно определяется источниками в виде токовых систем, находящимися за пределами земной поверхности в её атмосфере В верхней части атмосферы (100 км и выше) — ионосфере — её молекулы ионизируются, формируя плотную холодную плазму, поднимающуюся выше, поэтому часть магнитосферы Земли выше ионосферы, простирающаяся на расстояние до трёх её радиусов, называется плазмосферой. Плазма удерживается магнитным полем Земли, но её состояние определяется его взаимодействием с солнечным ветром — потоком плазмы солнечной короны.

КАРТА ИЗОГОН МАГНИТНОГО ПОЛЯ

СКЛОНЕНИЕ МАГНИТНОЙ СТРЕЛКИ
Угол между геодезическим меридианом данной точки и ее магнитным меридианом, направленным на север, называется склонением магнитной стрелки или магнитным склонением, обозначаемым как δ Магнитное склонение считается положительным, если северный конец магнитной стрелки отклонён к востоку от геодезического меридиана (восточное склонение), и отрицательным, если он отклонён к западу (западное склонение).

ВЫЧИСЛЕНИЕ МАГНИТНОГО СКЛОНЕНИЯ
Величину магнитного склонения на текущий момент времени можно вычислить по следующей формуле:

ОБОРУДОВАНИЕ ДЛЯ ОПРЕДЕЛЕНИЯ АЗИМУТОВ В ПОЛЕ
МАГНИТНЫЕ КОМПАС И ГИРОКОМПАС

В полевых условиях поддаются определению только магнитный и географический азимуты. Дирекционный угол непосредственно на местности измерить невозможно. Его можно только вычислить по приведённым выше формулам.

ГИРОСКОП
Гироскоп (от др.-греч. γῦρος — круг + σκοπέω — смотрю) — устройство, способное реагировать на изменение углов ориентации тела, на котором оно установлено, относительно инерциальной системы отсчета. Простейший пример гироскопа — юла (волчок).
Гирокомпас — это, по существу, гироскоп, то есть вращающееся колесо (ротор), установленное в кардановом подвесе, который обеспечивает оси ротора свободную ориентацию в пространстве.

КАРДАНОВ ПОДВЕС

ИСТОРИЯ СОЗДАНИЯ ГИРОКОМПАСА
Гироскоп был запатентован в 1885 году датчанином Мариусом Герардусом ван ден Босом, но его гироскоп никогда должным образом не работал. Француз Артур Кребс в 1889 году сконструировал маятниковый гирокомпас для экспериментов на подводной лодке «Gymnote». Это позволило Gymnote преодолеть морскую блокаду в 1890 году. В 1903 году немец Герман Аншютц-Кемпфе сконструировал работающий гирокомпас и получил патент на его изобретение. В 1908 году Аншютц-Кемпфе и американский изобретатель Элмер Сперри патентуют гироскоп в Германии и США соответственно. Когда Сперри попытался продать своё устройство германскому военно-морскому флоту, Аншютц-Кемпфе подал в суд иск за нарушение патентного законодательства. Сперри утверждал, что патент Аншютц-Кемпфе недействителен, так как патентуемое устройство незначительно отличается от гироскопа ван ден Боса. Патентным экспертом по иску выступал знаменитый физик Альберт Эйнштейн. Сначала он согласился со Сперри, но затем изменил своё мнение, признав, что патент Аншютц-Кемпфе был действителен, а Сперри нарушил авторское право, использовав специфический способ затухания. Аншютц-Кемпфе выиграл процесс в 1915 году

ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ ГИРОКОМПАСА
Морской гирокомпас обычно основывается на гиросфере. Гиросфера — полый металлический шар, внутри которого имеются вращающиеся с высокой скоростью гироскопы. Привод вращения — электродвигатели. Сфера герметична, заполнена водородом для уменьшения потерь на трение, содержит на дне небольшое количество смазывающего масла. Для запитки электродвигателя сферы выполняются составными с токоизолируюшим бандажом между частями, питающее напряжение (обычно переменное высокой частоты) подаётся через токопроводящую жидкость, состоящую из воды, глицерина, этилового спирта и борной кислоты, в которой плавает сфера.
Существует два способа предотвращения контакта сферы с дном или крышкой сосуда, в обоих случаях они основаны на применении ртути как жидкости с высокой плотностью, нерастворимой в воде. В первом случае небольшой количество, около 50 мл, ртути выливается на дно сосуда, а сфера изготавливается с небольшой отрицательной плавучестью и тонет в спецжидкости до тех пор, пока не достигает слоя ртути, ниже которого уже не тонет из-за большого веса вытесняемой ртути. Во втором варианте сфера имеет положительную плавучесть и коническое углубление наверху, в которое опять же наливается ртуть, и входит конический выступ крышки сосуда. На советских и российских гирокомпасах применяется первый способ, жидкость подлежит замене не реже, чем раз в полгода из-за ухудшения её свойств. В некоторых современных гирокомпасах применяется динамическое удержание гиросферы в струе поддерживающей жидкости, непрерывно прокачиваемой насосом снизу вверх. В этом случае ртутной подушки нет, такие гирокомпасы дешевле и проще в обслуживании.

ГИРОСФЕРА
Гиросфера гирокомпаса типа Аншютц — Кемпфе в разрезе

ГИРОКОМПАС АГ-1

GYROMAT 5000

МАГНИТНЫЙ КОМПАС
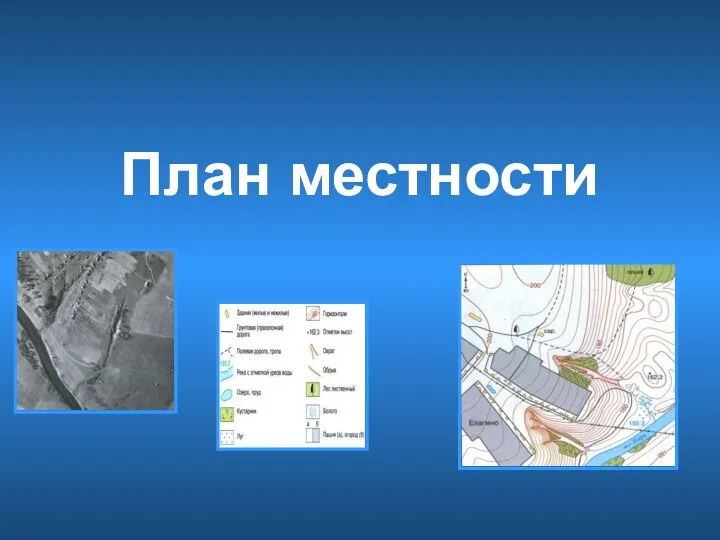Ко́мпас (итал. compassio; от compassare — измерять шагами[1]; в профессиональной речи моряков: компа́с) — устройство, облегчающее ориентирование на местности путём указания на магнитные полюса Земли и стороны света.

ВИДЫ МАГНИТНЫХ КОМПАСОВ
Горный компас Брантона
Электронный компас в системе GPS
Компас Адрианова
Буссоль

ОСНОВНЫЕ ЗАДАЧИ ГЕОДЕЗИИ
ПРЯМАЯ И ОБРАТНАЯ ГЕОДЕЗИЧЕСКИЕ ЗАДАЧИ

СИСТЕМА КООРДИНАТ ГАУССА (ПЛОСКИЕ ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ

ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Прямая геодезическая задача (ПГЗ) заключается в нахождении координат точки 2 по известным координатам точки 1, а также по известному дирекционному углу направления 1-2 и горизонтальному проложению между точками 1 и 2.
Горизонтальное проложение – проекция наклонного (истинного) расстояния между точками на горизонтальную плоскость.

РЕШЕНИЕ ПГЗ

ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Обратная геодезическая задача (ОГЗ) заключается в нахождении дирекционного угла и горизонтального проложения между точками 1 и 2 по их известным координатам

РЕШЕНИЕ ОГЗ

ПЕРЕХОД ОТ РУМБОВ К ДИРЕКЦИОННЫМ УГЛАМ

ВЫЧИСЛЕНИЕ ГОРИЗОНТАЛЬНОГО ПРОЛОЖЕНИЯ