Водные свойства почв

Пористость почв
Вопрос № 1

Водные свойства почв
Пористость почв
Значения пористости в разных почвенных горизонтах:
Величина пористости в разных почвах и в разных горизонтах одной и той же почвы варьирует в широких пределах - от 25 до 80 % в минеральных почвах.
В чисто органогенных горизонтах, например в торфах и лесных подстилках, она может превышать 90 %.
В верхних, гумусовых горизонтах минеральных почв величина пористости бывает обычно повышенной (50-60 %) за счет хорошо выраженной структуры, наличия ходов корней, ходов роющих животных и насекомых и т. д.
Книзу пористость уменьшается, доходя до 40‑45 % в глинистых и суглинистых неоглеенных породах и до 35‑40 % в песчаных.
В оглеенных суглинистых и глинистых породах она уменьшается, как будет показано ниже, до 25-30 %.
Размер пор тем больше, чем грубее гранулометрический состав, т. е. чем крупнее частицы, из которых состоит почва.
!

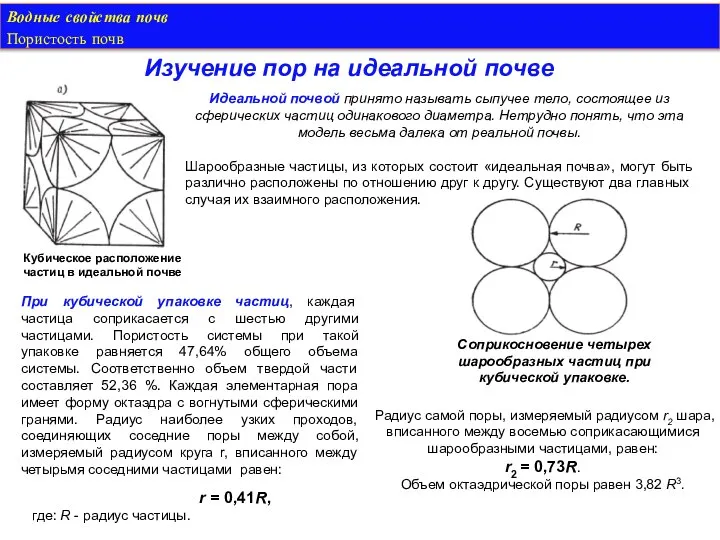
Водные свойства почв
Пористость почв
Изучение пор на идеальной почве
Идеальной почвой принято называть сыпучее тело, состоящее из сферических частиц одинакового диаметра. Нетрудно понять, что эта модель весьма далека от реальной почвы.
Шарообразные частицы, из которых состоит «идеальная почва», могут быть различно расположены по отношению друг к другу. Существуют два главных случая их взаимного расположения.
Кубическое расположение частиц в идеальной почве
При кубической упаковке частиц, каждая частица соприкасается с шестью другими частицами. Пористость системы при такой упаковке равняется 47,64% общего объема системы. Соответственно объем твердой части составляет 52,36 %. Каждая элементарная пора имеет форму октаэдра с вогнутыми сферическими гранями. Радиус наиболее узких проходов, соединяющих соседние поры между собой, измеряемый радиусом круга r, вписанного между четырьмя соседними частицами равен:
r = 0,41R,
где: R - радиус частицы.
Соприкосновение четырех шарообразных частиц при кубической упаковке.
Радиус самой поры, измеряемый радиусом r2 шара, вписанного между восемью соприкасающимися шарообразными частицами, равен:
r2 = 0,73R.
Объем октаэдрической поры равен 3,82 R3.

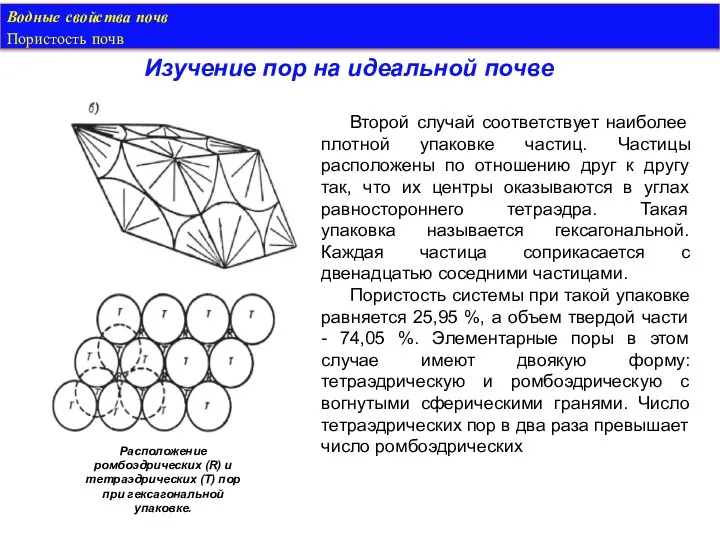
Водные свойства почв
Пористость почв
Изучение пор на идеальной почве
Второй случай соответствует наиболее плотной упаковке частиц. Частицы расположены по отношению друг к другу так, что их центры оказываются в углах равностороннего тетраэдра. Такая упаковка называется гексагональной. Каждая частица соприкасается с двенадцатью соседними частицами.
Пористость системы при такой упаковке равняется 25,95 %, а объем твердой части - 74,05 %. Элементарные поры в этом случае имеют двоякую форму: тетраэдрическую и ромбоэдрическую с вогнутыми сферическими гранями. Число тетраэдрических пор в два раза превышает число ромбоэдрических
Расположение ромбоэдрических (R) и тетраэдрических (Т) пор при гексагональной упаковке.

Водные свойства почв
Пористость почв
Выводы:
Поровое пространство «идеальной почвы» представляет собой совокупность пустот различной формы и различного размера, соединяющихся между собой в разных направлениях проходами более узкими, нежели поперечник самих пустот.
Характерной чертой пористости является ритмическая изменчивость в пространстве поперечника почвенных пор, осуществляющаяся на весьма малых расстояниях.
Почвенное поровое пространство можно представить в виде пространственной трехмерной сетки, состоящей как бы из узелков (пор) различной формы и различ­ного размера, соединенных друг с другом перетяжками (более узкими проходами между порами).
Вероятно, что в почвах и грунтах грубого гранулометрического состава - песчаного, гравийного, особенно при условии окатанности отдельных частиц, - поры по своей формемогут приближаться к порам «идеальной почвы».
В «почвах же и грунтах более тяжелого гранулометрического состава - суглинистых и глинистых, в которых содержится большее или меньшее количество частиц глинных минералов, обладающих пластинчатой формой, форма пор может значительно отличаться от формы пор «идеальной почвы».

Водные свойства почв
Пористость почв
Пористость перегнойных горизонтов
Пористость перегнойных горизонтов в почвах самых разных типов по большей части варьирует в пределах 50‑60%, т. е., значительно превышает пористость «идеальной почвы» даже при самой рыхлой - кубической - упаковке частиц.
Причины этого нужно искать, естественно, в том, что именно в гумусовом горизонте, как правило, наиболее отчетливо бывает выражена структура, т.е. агрегированность почвенных частиц. Совершенно понятно, что когда почва состоит из более или менее крупных комочков, которые в свою очередь состоят тоже из комочков или из элементарных частиц и, следовательно, обладают своей, внутриагрегатной пористостью, то общая пористость почвы от этого значительно повышается. Кроме того, в перегнойных горизонтах, более чем в каких‑либо других, бывает развита корневая система растений, а также ходы различных мелких роющих животных (дождевых червей, личинок насекомых и т. д.). Эти явления также сильно повышают пористость почвы.

Водные свойства почв
Пористость почв
Пористость глубоких неоглеенных горизонтов
В более глубоких горизонтах почвы (кроме оглеенных) величина пористости равным образом материнских пород, обычно лежит гораздо ближе к пористости «идеальной почвы» при кубической упаковке (47,64 %), нежели при гексагональной (25,95 %), иногда превышая даже первую из этих величин.
Все эти неоглеенные суглинистые грунты, особенно лёссовидные, и нижние горизонты почв обладают микроструктурой. Они состоят из мелких агрегатов, диаметр которых обычно измеряется величинами порядка сотых долей миллимет­ра. В соответствии с этим и в указанных почвенных горизонтах и в грунтах имеется по меньшей мере две системы пор: поры межагрегатные и поры внутриагрегатные.

Водные свойства почв
Пористость почв
Близость общей пористости к величине пористости при кубической упаковке оказывается совершенно случайной. На самом деле эта величина (45,1 %) может быть обусловлена микроструктурой почвенных горизонтов и их двоякой (межагрегатной и внутриагрегатной) пористостью, причем упаковка элементарных частиц в агрегатах и самих агрегатов может быть достаточно близкой к наиболее плотной, т. е. гексагональной.
Однако межагрегатная пористость может достигать указанных величин лишь в тех случаях, когда порода представляет собой нанос, который образовался путем отложения готовых уже агрегатов. В почвах межагрегатная пористость может возникать и иначе - путем растрескивания, распада ранее образовавшихся почвенных комков. В этих случаях величина межагрегатной пористости может быть значительно меньше и может сильно изменяться во времени в зависимости от влажности почвы.

Водные свойства почв
Пористость почв
В верхних, гумусовых горизонтах почв, в особенности хорошо оструктуренных (черноземы), как уже было отмечено выше, общая пористость гораздо больше - чаще всего около 60 %. Возникновение такой пористости может быть объяснено аналогичным образом, но с допущением уже трехстепенной агрегированности. Микроагрегаты, состоящие из элементарных частиц, в этом случае в свою очередь склеиваются в макроагрегаты опять-таки с гексагональной упаковкой.
Общая пористость такой системы будет равна:
Пористость внутримакроагрегатная
+
Пористость межмакроагретаня
+
Пористость внутримикроагрегатная
Таким образом, при трехстепенной агрегированности общая пористость оказывается равной 60 %, что соответствует наблюдаемой в природе пористости гумусовых горизонтов разных почв, в особенности черноземов.

Водные свойства почв
Пористость почв
Пористость оглеенных горизонтов
Пористость резко уменьшается при оглеении, и в этом случае ее величина начинает приближаться к пористости «идеальной почвы» при гексагональной упаковке (25,95 %).
Как следствие уменьшения пористости, при оглеении возрастает плотность сложения, то есть при оглеении происходит уплотнение почвенной массы.
При оглеении разрушается микроструктура, присущая нижним почвенным горизонтам в неоглеенном состоянии, а следовательно, исчезает и межагрегатная пористость.
Элементарные частицы укладываются более плотно, в результате чего и возникает пористость, близкая по своей величине к пористости «идеальной почвы» при гексагональной упаковке.

Строение и свойства воды
Вопрос № 2

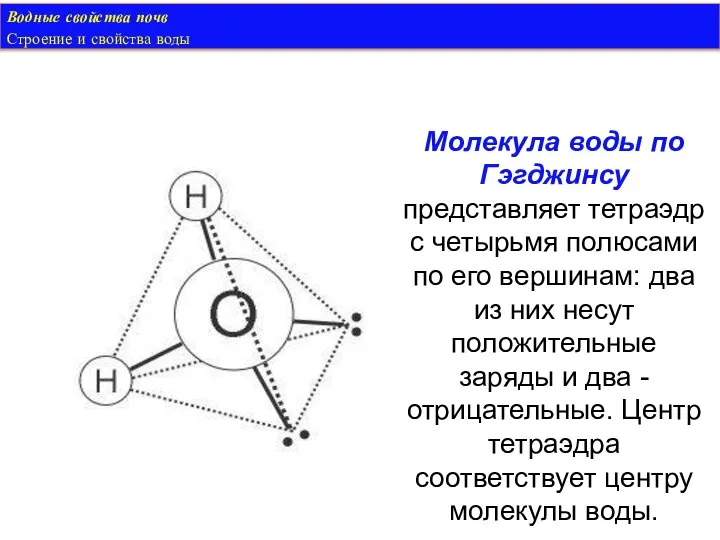
Водные свойства почв
Строение и свойства воды
Молекула воды по Гэгджинсу представляет тетраэдр с четырьмя полюсами по его вершинам: два из них несут положительные заряды и два - отрицательные. Центр тетраэдра соответствует центру молекулы воды.

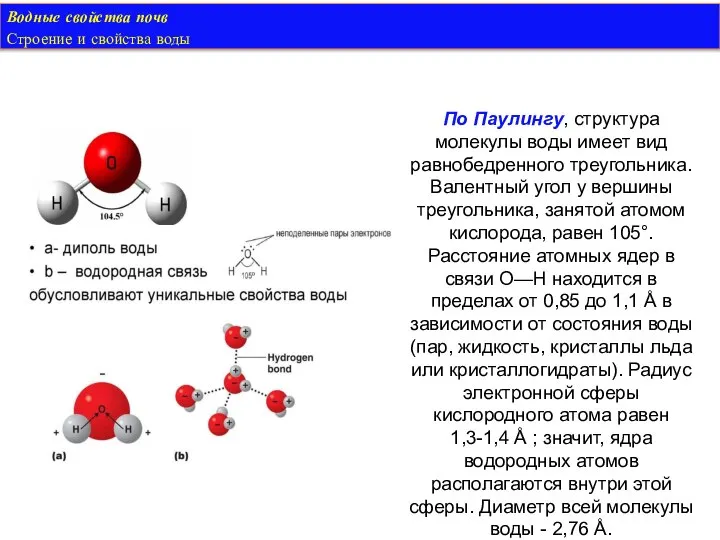
Водные свойства почв
Строение и свойства воды
По Паулингу, структура молекулы воды имеет вид равнобедренного треугольника. Валентный угол у вершины треугольника, занятой атомом кислорода, равен 105°. Расстояние атомных ядер в связи О—Н находится в пределах от 0,85 до 1,1 Å в зависимости от состояния воды (пар, жидкость, кристаллы льда или кристаллогидраты). Радиус электронной сферы кислородного атома равен 1,3-1,4 Å ; значит, ядра водородных атомов располагаются внутри этой сферы. Диаметр всей молекулы воды - 2,76 Å.

Водные свойства почв
Строение и свойства воды
Результаты определения молекулярного веса водяного пара указывают на то, что он практически состоит из свободных молекул воды (Н2О), а в жидком состоянии вода ассоциирована.
Наряду с простыми молекулами, она содержит и более сложные молекулярные агрегаты из двух-трех и более молекул.
Такие агрегаты постоянно возникают и вновь распадаются, что можно выразить схемой:
хH2О↔ (H2О)х
Водородная связь

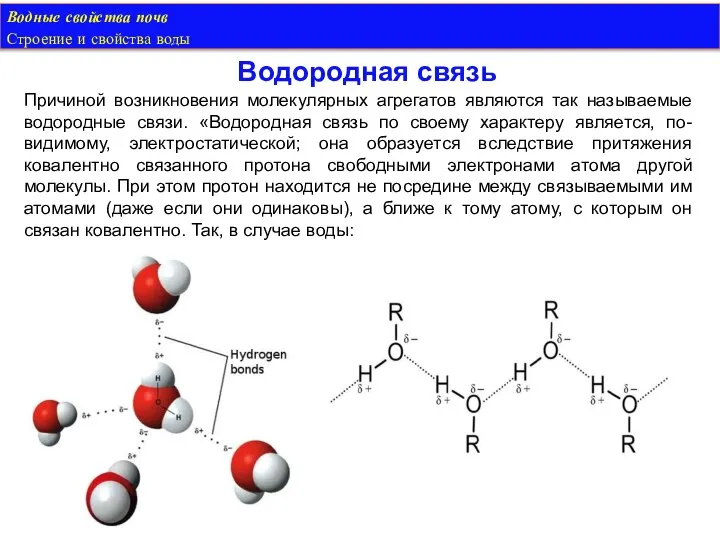
Водные свойства почв
Строение и свойства воды
Причиной возникновения молекулярных агрегатов являются так называемые водородные связи. «Водородная связь по своему характеру является, по-видимому, электростатической; она образуется вследствие притяжения ковалентно связанного протона свободными электронами атома другой молекулы. При этом протон находится не посредине между связываемыми им атомами (даже если они одинаковы), а ближе к тому атому, с которым он связан ковалентно. Так, в случае воды:
Водородная связь

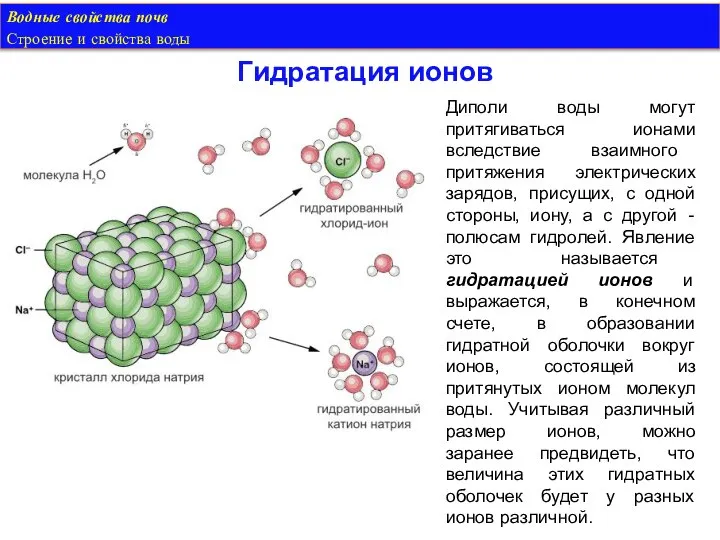
Водные свойства почв
Строение и свойства воды
Гидратация ионов
Диполи воды могут притягиваться ионами вследствие вза­имного притяжения электрических зарядов, присущих, с одной стороны, иону, а с другой - полюсам гидролей. Явление это на­зывается гидратацией ионов и выражается, в конечном счете, в образовании гидратной оболочки вокруг ионов, состоящей из притянутых ионом молекул воды. Учитывая различный размер ионов, можно заранее предвидеть, что величина этих гидратных оболочек будет у разных ионов различной.

Осмотические явления в почвах
Вопрос № 3

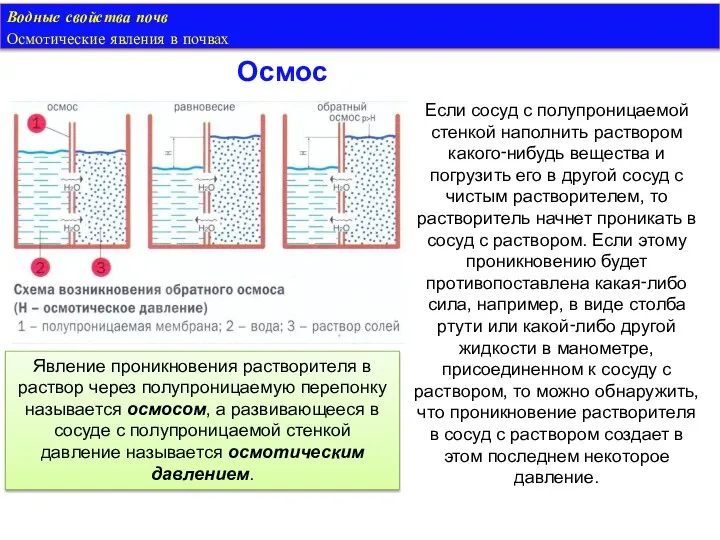
Водные свойства почв
Осмотические явления в почвах
Осмос
Если сосуд с полупроницаемой стенкой наполнить раствором какого‑нибудь вещества и погрузить его в другой сосуд с чистым растворителем, то растворитель начнет проникать в сосуд с раствором. Если этому проникновению будет противопоставлена какая‑либо сила, например, в виде столба ртути или какой‑либо другой жидкости в манометре, присоединенном к сосуду с раствором, то можно обнаружить, что проникновение растворителя в сосуд с раствором создает в этом последнем некоторое давление.
Явление проникновения растворителя в раствор через полупроницаемую перепонку называется осмосом, а развивающееся в сосуде с по­лупроницаемой стенкой давление называется осмотическим давлением.

Водные свойства почв
Осмотические явления в почвах
Осмос
Осмотическое давление подчиняется определенным количественным закономерностям, установленным Вант-Гоффом.
Величина осмотического давления подчиняется тому же зако­ну, что и величина давления газа,
Р = RсТ,
где Р - осмотическое давление растворенного вещества, R - га­зовая постоянная, с - концентрация раствора, Т - абсолютная температура.
Причиной осмотического давления является то притяжение, которое оказывают частицы растворенного вещества в воде. Это притяжение заставляет проникать воду в сосуд с полупроницаемой стенкой, когда в нем будет находиться раствор, и он будет погружен в воду. По этому воз­зрению агентом, вызывающим осмотическое давление, является взаимное притяжение между частицами растворенного вещества и растворителя.

Водные свойства почв
Осмотические явления в почвах
Суть осмотического давления
Если считать, что осмотическое давление есть разность давлений диффузии чистого растворителя и растворителя в растворе, то величина осмотического давления будет равна разности между энергией моле­кул чистого растворителя и энергией его же молекул в растворе.
В основе явления осмоса лежит связывание молекул растворителя с молекулами или ионами растворенного вещества. Количественно же под осмотическим давлением следует понимать величину гидростатического давления, которую необходимо приложить к раствору, для того чтобы уравновесить его с чистым растворителем, отделенным от него полупроницаемой мембраной.

Водные свойства почв
Осмотические явления в почвах
Приложение осмотического давления к почве
В почве с явлениями осмоса мы сталкиваемся в двух главных случаях.
Взаимодействие воды и обменных катионов. Обменные катионы притягиваются поверхностью почвенных коллоидных частиц. Одновременно эти катионы притягивают к себе из почвенного раствора дипольные молекулы воды, которые стремятся окружить каждый обменный катион со всех сторон, создать вокруг него водную оболочку и, отжать, отчленить его от поверхности почвенной частицы. Вот это отжимающее усилие можно рассматривать как проявление осмотического давления.
Почвенный раствор имеет неодинаковую концентрацию в разных участках почвенной толщи. В этом случае наблюдается не только диффузия растворенных веществ из участков с более высокой их концентрацией к участкам с более низкой концентрацией, но одновременно и встречная диффузия воды в обратном направлении.
Оба эти процесса в своей основе имеют взаимодействие между молекулами или ионами почвенного раствора и дипольными молекулами воды, т. е. оба эти процесса по своей природе являются осмотическими. Су­щественное значение эти явления могут иметь лишь при более или менее высокой концентрации почвенного раствора и значи­тельной разнице концентраций. Одновременное существование обоих указанных процессов экспериментально было показано А. Ф. Лебедевым.

Капиллярные явления в почвах
Вопрос № 4

Водные свойства почв
Капиллярные явления в почвах
Капиллярные явления имеют в своей основе:
молекулярное давление и пленочное натяжение в поверхностных слоях жидкости;
образование мениска при взаимодействии жидкости с поверхностью твердого тела в узких порах;
изменение давления в жидкости непосредственно под мениском в сторону плюса или минуса и, в соответствии с этим, передвижение жидкости (поднятие по капилляру вверх или опускание в нем).

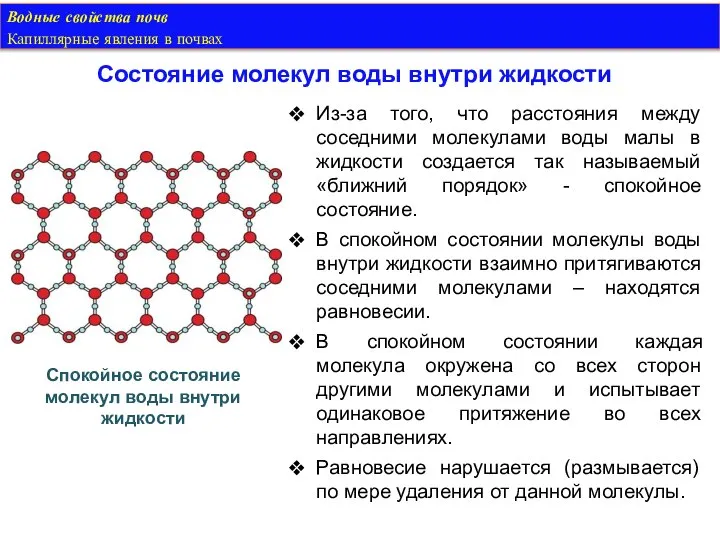
Водные свойства почв
Капиллярные явления в почвах
Из-за того, что расстояния между соседними молекулами воды малы в жидкости создается так называемый «ближний порядок» - спокойное состояние.
В спокойном состоянии молекулы воды внутри жидкости взаимно притягиваются соседними молекулами – находятся равновесии.
В спокойном состоянии каждая молекула окружена со всех сторон другими молекулами и испытывает одинаковое притяжение во всех направлениях.
Равновесие нарушается (размывается) по мере удаления от данной молекулы.
Спокойное состояние молекул воды внутри жидкости
Состояние молекул воды внутри жидкости

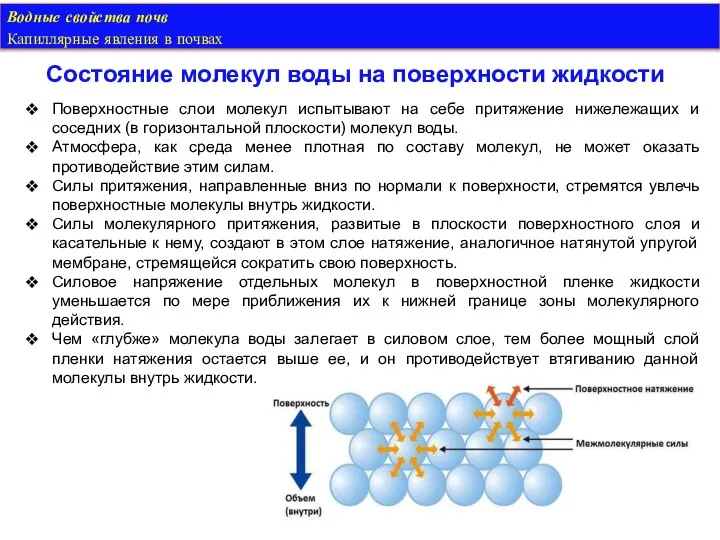
Водные свойства почв
Капиллярные явления в почвах
Состояние молекул воды на поверхности жидкости
Поверхностные слои молекул испытывают на себе притяжение нижележащих и соседних (в горизонтальной плоскости) молекул воды.
Атмосфера, как среда менее плотная по составу молекул, не может оказать противодействие этим силам.
Силы притяжения, направленные вниз по нормали к поверхности, стремятся увлечь поверхностные молекулы внутрь жидкости.
Силы молекулярного притяжения, развитые в плоскости поверхностного слоя и касательные к нему, создают в этом слое натяжение, аналогичное натянутой упругой мембране, стремящейся сократить свою поверхность.
Силовое напряжение отдельных молекул в поверхностной пленке жидкости уменьшается по мере приближения их к нижней границе зоны молекулярного действия.
Чем «глубже» молекула воды залегает в силовом слое, тем более мощный слой пленки натяжения остается выше ее, и oн противодействует втягиванию данной молекулы внутрь жидкости.

Водные свойства почв
Капиллярные явления в почвах
Поверхностное натяжение жидкости
Силы поверхностного натяжения и молекулярного давления тесно связаны между собой.
По Гауссу, для вывода молекул жидкости из глубины на поверхность и увеличения поверхности необходимо преодолеть молекулярное давление и пленочное натяжение.
Очевидно, для изменения поверхности жидкости S на величину dS нужно совершить работу, равную dr. Оказывается, что работа dr пропорциональна приращению поверхности dS, поэтому можно написать равенство:
где а - работа для вывода одной молекулы на поверхность; n - число молекул в 1 см2 поверхностного слоя жидкости.
Величина an = Ϭ называется коэффициентом поверхностного натяжения жидкости:

Водные свойства почв
Капиллярные явления в почвах
Поверхностное натяжение жидкости
Сила f, действующая таким образом на линию, длина которой m, равна:
Сила, с которой поверхность стремится сократиться, отнесенная к единице длины контура на поверхности или действующая на единицу длины линии, являющейся границей поверхности жидкости, перпендикулярно к ней и по касательной к поверхности жидкости, называется поверхностным натяжением.
Величина может быть выражена в мг/мм.

Водные свойства почв
Капиллярные явления в почвах
Капиллярная постоянная
Капиллярная постоянная жидкости численно равна капиллярному натяжению поверхности жидкости, т. е. равна той силе, которую надо приложить к единице длины какого-нибудь контура на поверхности, чтобы уравновесить поверхностное натяжение.
Капиллярную постоянную находят из уравнения:
где а2 - капиллярная постоянная; - поверхностное натяжение жидкости; - плотность жидкости
Капиллярную постоянную (а2) выражают в мм2:
где r - радиус капилляра, h - высота поднятия жидкости в капилляре.

Водные свойства почв
Капиллярные явления в почвах
Капиллярная постоянная
Если r = 1, то a2 = h или капиллярная постоянная данной жидкости численно равна высоте подъема этой жидкости в трубке, радиус канала которой равен 1 мм и стенки которой жидкостью вполне смачиваются.
Поверхностное натяжение всех жидкостей уменьшается с повышением температуры.
При критической температуре для каждой жидкости поверхностное натяжение обращается в нуль.

Водные свойства почв
Капиллярные явления в почвах
Молекулярное давление
Для точного вычисления молекулярного давления до сих пор не найдено соответствующих методов. Приблизительно оно может быть вычислено по формуле:
где Р - молекулярное давление; k - коэффициент теплового расширения жидкости; β - коэффициент ее сжимаемости; Т - абсолютная температура.
Величины поверхностного натяжения и молекулярного давления входят составляющими в ряд расчетных формул при вычислении высоты капиллярного подъема влаги (Лапласа, Жюрена и др.).

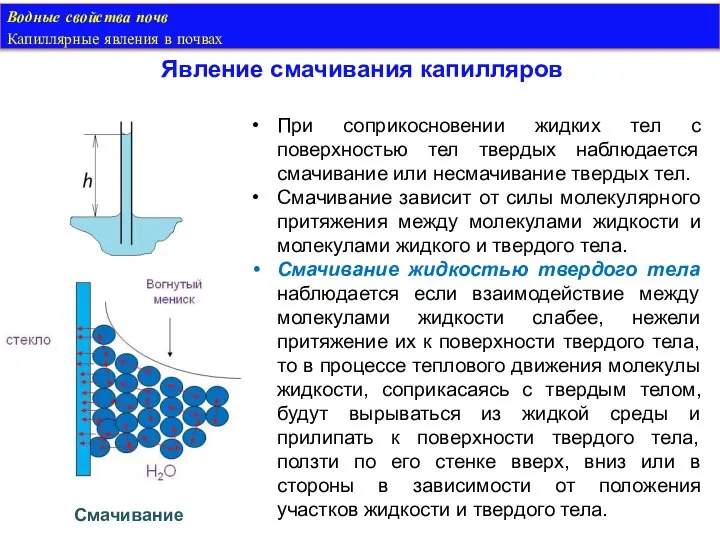
Водные свойства почв
Капиллярные явления в почвах
Явление смачивания капилляров
При соприкосновении жидких тел с поверхностью тел твердых наблюдается смачивание или несмачивание твердых тел.
Смачивание зависит от силы молекулярного притяжения между молекулами жидкости и молекулами жидкого и твердого тела.
Смачивание жидкостью твердого тела наблюдается если взаимодействие между молекулами жидкости слабее, нежели притяжение их к поверхности твердого тела, то в процессе теплового движения молекулы жидкости, соприкасаясь с твердым телом, будут вырываться из жидкой среды и прилипать к поверхности твердого тела, ползти по его стенке вверх, вниз или в стороны в зависимости от положения участков жидкости и твердого тела.
Смачивание

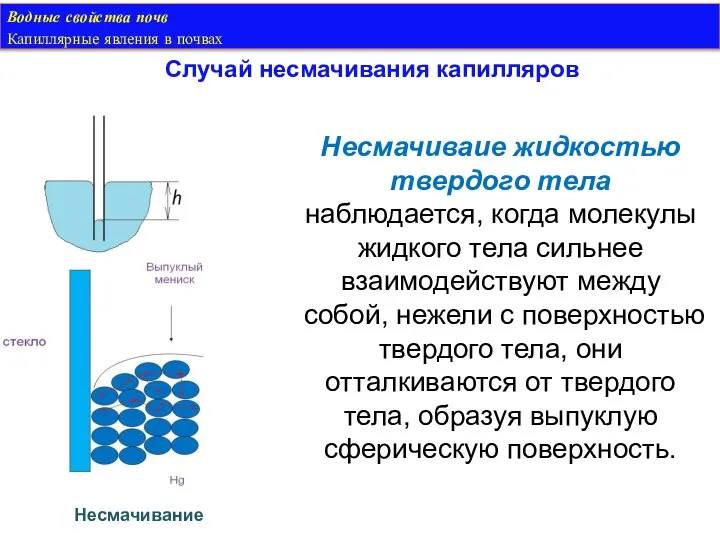
Водные свойства почв
Капиллярные явления в почвах
Случай несмачивания капилляров
Несмачиваие жидкостью твердого тела наблюдается, когда молекулы жидкого тела сильнее взаимодействуют между собой, нежели с поверхностью твердого тела, они отталкиваются от твердого тела, образуя выпуклую сферическую поверхность.
Несмачивание

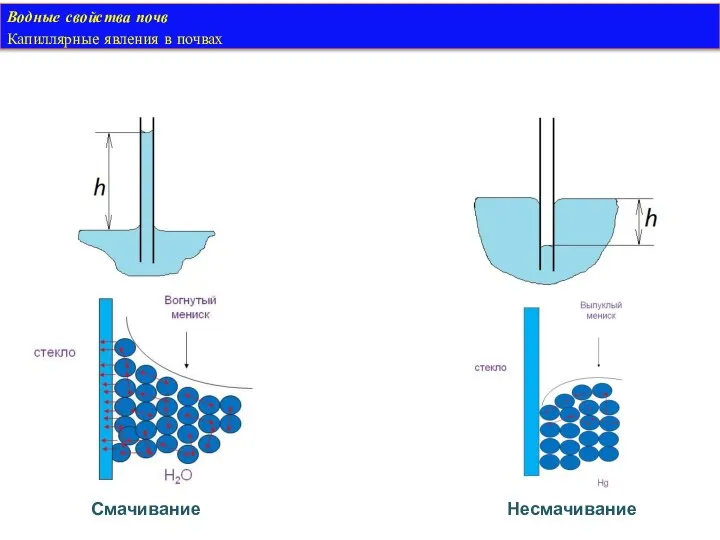
Водные свойства почв
Капиллярные явления в почвах
Смачивание
Несмачивание

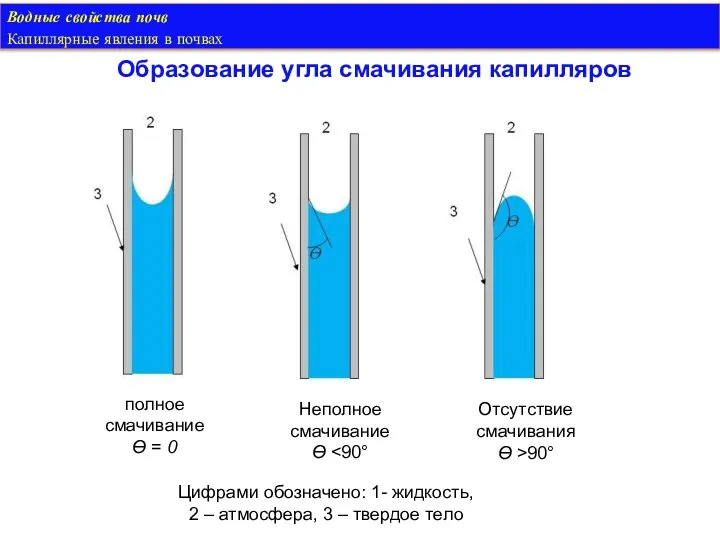
Водные свойства почв
Капиллярные явления в почвах
Образование угла смачивания капилляров
По границе контакта атмосфера - поверхность жидкости - погруженная в жидкость часть твердого тела между касательными плоскостями к поверхности твердого тела и к поверхности жидкости образуется двугранный угол, получивший название угла смачивания или краевого угла (Ɵ).
Чем совершеннее жидкость смачивает поверхность твердого тела, тем краевой угол меньше:
При полном смачивании, например, бензин, масло - сталь, Ɵ = 0 - мениск в капилляре сильно вогнут
полное смачивание
Ɵ = 0
Цифрами обозначено: 1- жидкость, 2 – атмосфера, 3 – твердое тело

Водные свойства почв
Капиллярные явления в почвах
Образование угла смачивания капилляров
При неполном смачивании (вода – минеральная часть почвы) Ɵ <90° - мениск в капилляре вогнут
При отсутствии смачивания (например, вода - парафин, ртуть - стекло) Ɵ >90° - мениск в капилляре выпуклый
Неполное смачивание
Ɵ <90°
Цифрами обозначено: 1- жидкость,
2 – атмосфера, 3 – твердое тело
Отсутствие смачивания
Ɵ >90°

Водные свойства почв
Капиллярные явления в почвах
Образование угла смачивания капилляров
Неполное смачивание
Ɵ <90°
Цифрами обозначено: 1- жидкость,
2 – атмосфера, 3 – твердое тело
Отсутствие смачивания
Ɵ >90°
полное смачивание
Ɵ = 0

Водные свойства почв
Капиллярные явления в почвах
Выражение смачивания капилляров
Смачивание количественно выражается величиной В.
Где 3.2 и т.д. - поверхностные энергии на границах: твердое тело (3) - воздух (2); твердое тело (3) -жидкость (1); жидкость (1) - воздух (2).
Смачивание тем больше (а краевой угол тем меньше), чем больше молекулярное сродство смачивающей жидкости и поверхности твердого тела, т. е. чем больше понижение поверхностного натяжения твердого тела.
В почвенных условиях угол смачивания обычно меньше 90°. На величине его сказываются свойства твердой фазы почвы и почвенного раствора.

Водные свойства почв
Капиллярные явления в почвах
Смачивание в капиллярах
В зоне смачивания по периферии твердого тела распределяется вода максимальная гигроскопическая и пленочная.
В случае заполнения жидкостью пор с малым диаметром (для условий вода - стекло d<8 мм) зона влияния краевых углов распространяется на весь просвет капилляра, образуя вогнутый или выпуклый мениск.
Если диаметр капилляра превосходит двойную толщину пленки жидкости, адсорбированной или десорбированной твердым телом, то под влиянием поверхностного натяжения жидкости в капилляре возникает новая ее форма - капиллярная, которая обладает свойствами, отличными от жидкости пограничного слоя.
При наличии смачивания мениск будет вогнутый; при отсутствии его – выпуклый.
Образование менисков в капилляре, заполненном жидкостью, изменяет давление в жидкости непосредственно под мениском.
В случае вогнутого мениска давление под ним меньше, нежели под плоской поверхностью жидкости и, наоборот, выпуклый мениск обусловливает давление, превышающее токовое под плоской поверхностью.

Водные свойства почв
Капиллярные явления в почвах
Формула Лапласа
Закономерности поведения жидкости в капиллярах получили математическое выражение в формуле Лапласа:
где Р - нормальное давление, производимое поверхностным слоем жидкости; К - нормальное давление на плоской поверхности;
- поверхностное натяжение жидкости; R1 и R2 - радиусы кривизны двух главных нормальных сечений поверхности мениска. Они считаются положительными, когда направлены внутрь жидкости (при выпуклом мениске), и отрицательными, когда направлены в атмосферу (при вогнутом мениске).
Если взять простейший случай, когда капилляр представляет собой цилиндр, то R1 и R2 будут между собой равны, и формула Лапласа примет следующий вид:

Водные свойства почв
Капиллярные явления в почвах
Поверхность плоская. Она может рассматриваться как часть шаровой поверхности с бесконечно большим радиусом
Нормальное давление плоской поверхности жидкости соответствует давлению (К) при одной атмосфере.
Поверхность мениска выпуклая. Формула Лапласа примет вид:
т. е. нормальное давление под выпуклым мениском больше, нежели под плоской поверхностью на величину
Поверхность мениска в капилляре вогнутая. Этот случай исключительно важен для передвижения капиллярной воды в почвах и грунтах. В этом случае формула Лапласа имеет вид:
Применение формулы Лапласа

Водные свойства почв
Капиллярные явления в почвах
Уравнение Жюрена
Под влиянием отрицательного давления под вогнутым мениском жидкость должна подняться в капилляре на такую высоту h, чтобы давление приподнятого жидкого столба на единицу площади, лежащей на высоте наружной, по отношению к капилляру, горизонтальной поверхности жидкости, сделалось бы равным величине
Следовательно
где: h – высота поднятия жидкости в капилляре; d – плотность жидкости.
Но, следовательно, и
Если жидкость вполне смачивает поверхность твердого тела, то краевой угол (Ɵ) будет равен нулю, а его косинус единице. Тогда последнее уравнение примет вид: