Слайд 2Логика - определение
Логика – наука, изучающая методы доказательств и опровержений.
Математическая логика –

современная форма логики, опирающаяся исключительно на формальные математические методы.
Слайд 3Множество
Множество – совокупность элементов, воспринимая как одно целое.
Элемент множества – один из

объектов, образующих множество.
Слайд 4Способы задания множеств
Перечисление {1,2,3}
Указание характеристического свойства {x|P(x)}
Задание порождающей процедуры

Слайд 5Операции над множествами
Объединение
Пересечение
Разность
Дополнение

Слайд 6Разбиение множества на классы
Разбиением множества А на подмножества (классы) называется система его

непустых подмножеств, обладающая следующими свойствами:
1) объединение всех подмножеств этой системы равно множеству А;
2) никакие два различные подмножества не содержат общих элементов.
Слайд 7Домашнее задание (База)
На олимпиаде по математике школьникам предложили решить три задачи: одну

по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии - 700, по тригонометрии - 600. 600 школьников решили задачи по алгебре и геометрии, 500 - по алгебре и тригонометрии, 400 - по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?






 Создание Web-сайта
Создание Web-сайта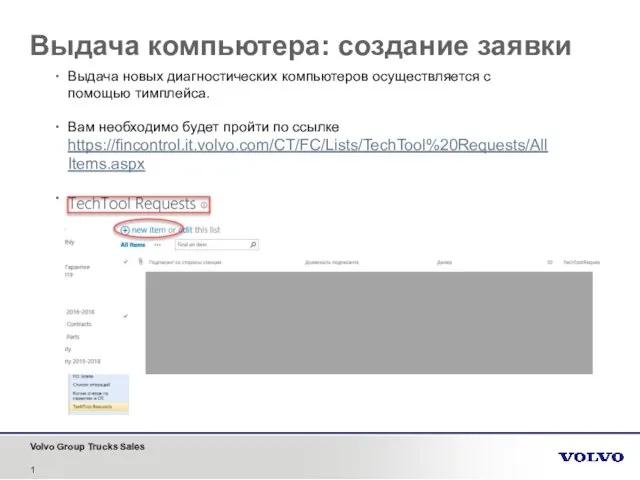 Выдача компьютера: создание заявки
Выдача компьютера: создание заявки Сегодня классный день. Ссылка в Профиле
Сегодня классный день. Ссылка в Профиле Операции над числами в языке Си++
Операции над числами в языке Си++ Создание презентации. Правила и инструменты
Создание презентации. Правила и инструменты Kvalitativní analýza dat
Kvalitativní analýza dat Системы шифрования
Системы шифрования Базовые технологии локальных сетей: Ethernet
Базовые технологии локальных сетей: Ethernet Everything You Wanted to Know but Were Afraid to Ask About QR Codes
Everything You Wanted to Know but Were Afraid to Ask About QR Codes Фрактальное сжатие
Фрактальное сжатие Моделирование этапов шифрования дисков и файлов с помощью средств Winserver 2016
Моделирование этапов шифрования дисков и файлов с помощью средств Winserver 2016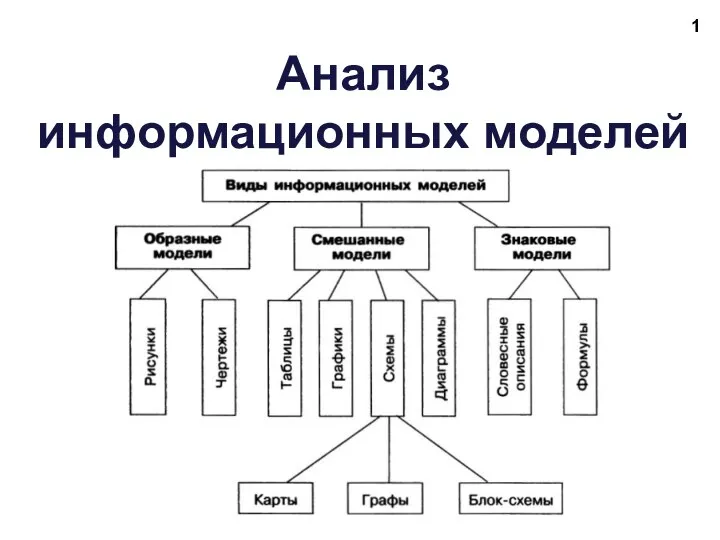 Матрица смежности. Анализ информационных моделей
Матрица смежности. Анализ информационных моделей Создание презентации к урокам
Создание презентации к урокам Сети. Самая простая сеть (network)
Сети. Самая простая сеть (network) Устройства ввода - вывода
Устройства ввода - вывода Задачи и направления развития информационного общества в Удмуртской Республике
Задачи и направления развития информационного общества в Удмуртской Республике Проекты FMCG 2020
Проекты FMCG 2020 Коммерческое предложение для ЗАО ЛугЦентроКуз
Коммерческое предложение для ЗАО ЛугЦентроКуз Зажигаем свечу. Создание анимации в программе Fdobe Photoshop
Зажигаем свечу. Создание анимации в программе Fdobe Photoshop Сайты, на которых размещаются темы итогового сочинения
Сайты, на которых размещаются темы итогового сочинения C гаджетами на ты. Смартфон
C гаджетами на ты. Смартфон Выбор способов построения 3D моделей. (3 занятие)
Выбор способов построения 3D моделей. (3 занятие) Линейный массив
Линейный массив Ступінь окиснення елементів
Ступінь окиснення елементів Проект НПК 2020. Приложение My Yakutsk
Проект НПК 2020. Приложение My Yakutsk Язык программирования C#
Язык программирования C# Информационно-технологическая инфраструктура организации. Программное обеспечение
Информационно-технологическая инфраструктура организации. Программное обеспечение Анализ информационных моделей
Анализ информационных моделей