Слайд 2Логика - это наука о формах и способах мышления.
Высказывание -это форма мышления,

которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними.
Высказывание может быть истинно или ложно.
Слайд 3В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь

два значения «истинно» и «ложно».
Истинно =1
Ложно=0
Слайд 4Для образования новых высказываний используются базовые логические операции:
логическое отрицание -операция не -

инверсия
логическое умножение - операция и - конъюнкция
логическое сложение - операция или - дизъюнкция
Слайд 5Логическое отрицание -операция не - инверсия
НЕ
А
А

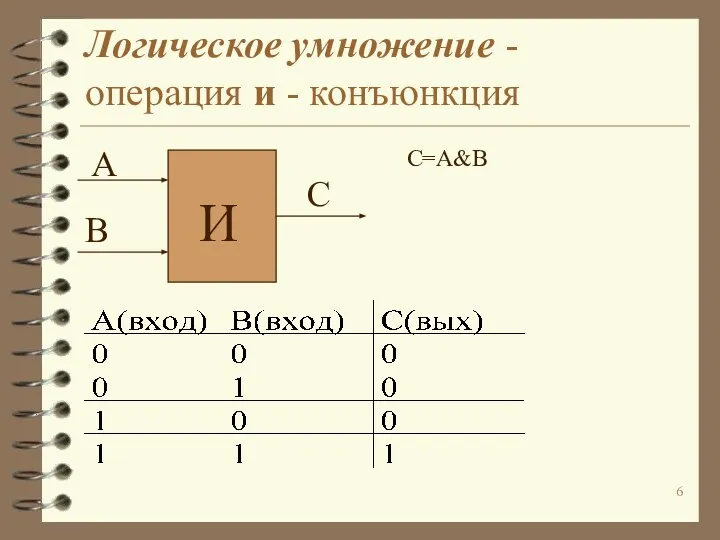
Слайд 6Логическое умножение - операция и - конъюнкция
C=A&B
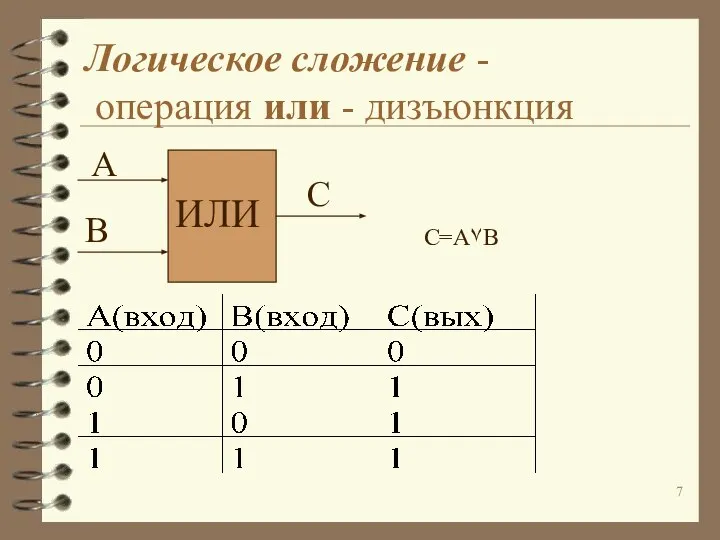
Слайд 7Логическое сложение -
операция или - дизъюнкция
ИЛИ
А
В
С
C=A۷B
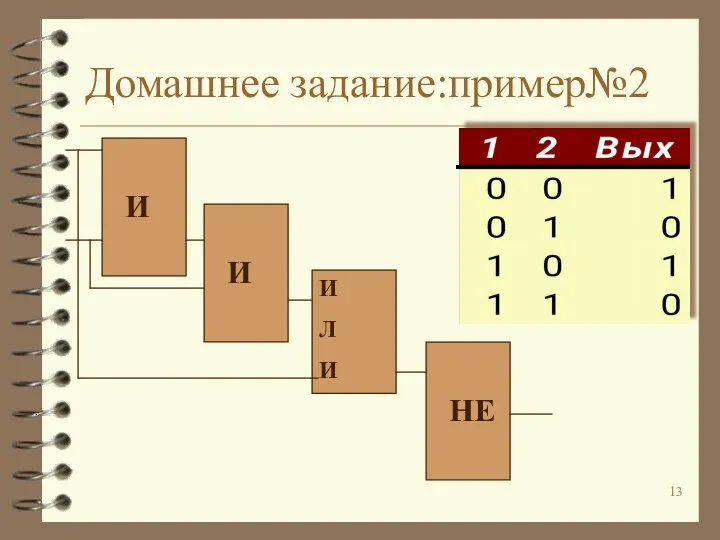
Слайд 18Пример№8
F(A,B,C)=(A^B) ۷ (A ۷ C)
=(A*B)+(A+C)

Слайд 19Пример№8
F(A,B,C)=(A^B) ۷ (A ۷ C)
=(A*B)+(A+C)

Слайд 20Пример№8
F(A,B,C)=(A^B) ۷ (A ۷ C)
=(A*B)+(A+C)

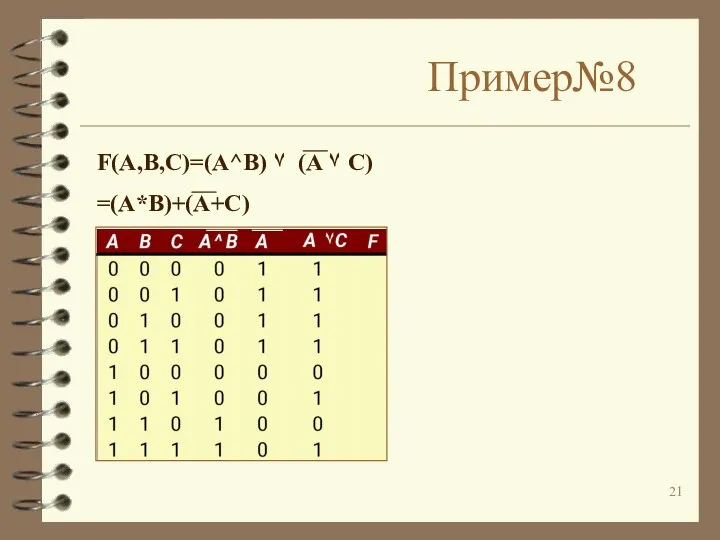
Слайд 21Пример№8
F(A,B,C)=(A^B) ۷ (A ۷ C)
=(A*B)+(A+C)
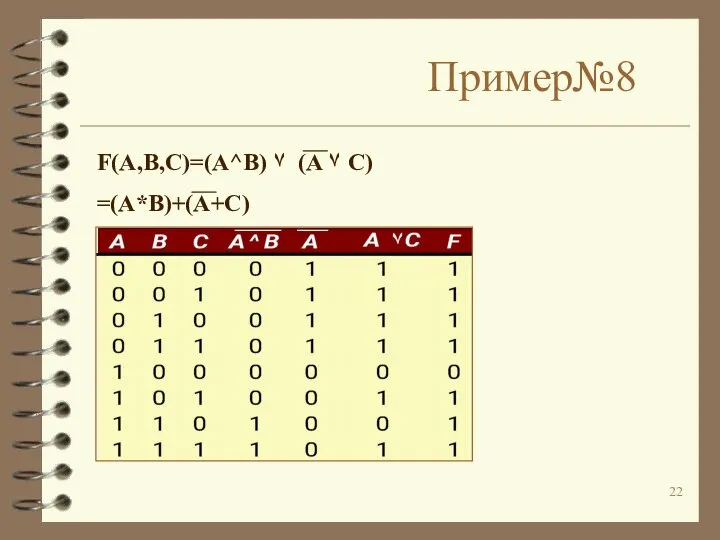
Слайд 22Пример№8
F(A,B,C)=(A^B) ۷ (A ۷ C)
=(A*B)+(A+C)
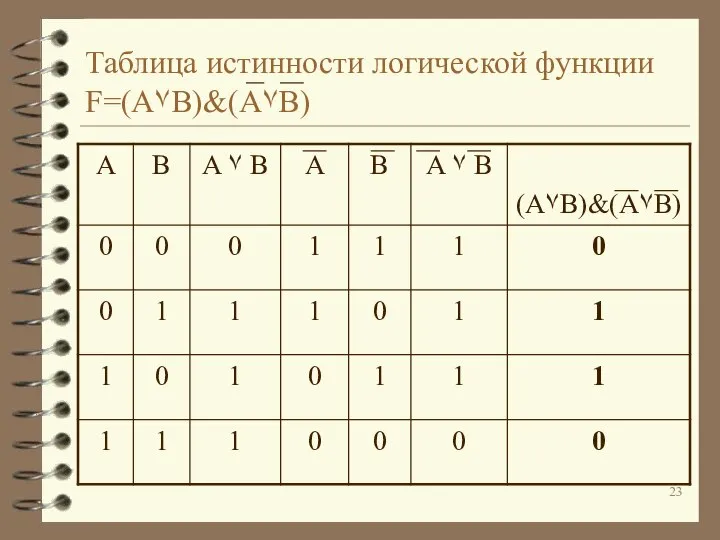
Слайд 23Таблица истинности логической функции
F=(A۷B)&(A۷B)
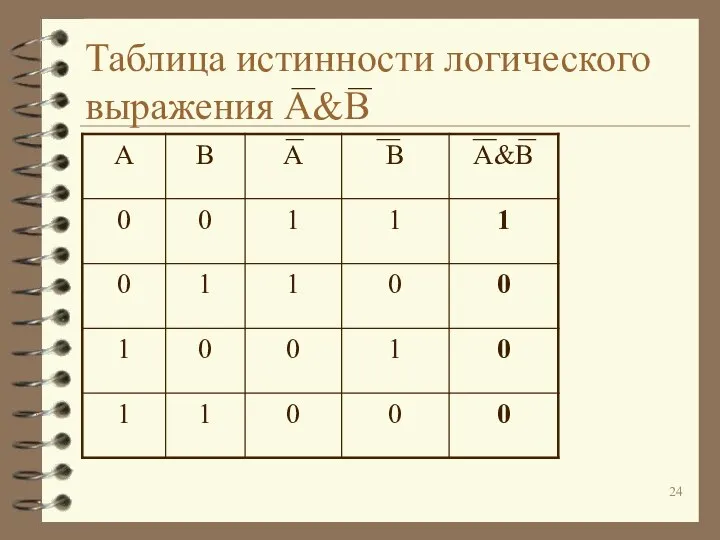
Слайд 24Таблица истинности логического выражения A&B
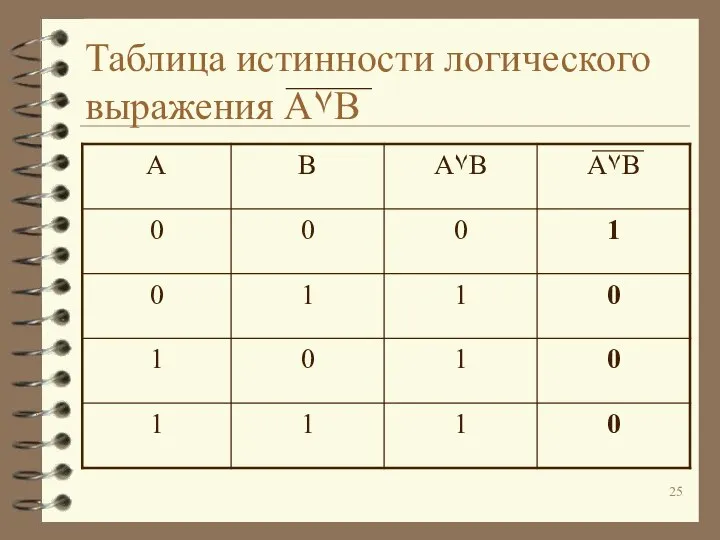
Слайд 25Таблица истинности логического выражения A۷B
Слайд 26Логические законы и правила преобразования логических выражений
Закон тождества: всякое высказывание тождественно самому

себе.
А=А
Закон непротиворечия: высказывание не может быть одновременно истинным и ложным.
А & А=1
Закон исключенного третьего. Высказывание может быть истинным, либо ложным, третьего не дано.
А ۷ А=1
Закон двойного отрицания: если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание.
А=А
Слайд 27Логические законы и правила преобразования логических выражений
Законы Моргана:
А ۷ В=А &

В
А & В=А ۷ В
Слайд 28Таблицы истинности совпадают, следовательно, логические выражения равносильны: A&B= A&B
Докажите , используя таблицы

истинности, что логические выражения А۷В и А&В равносильны
Слайд 29Домашнее задание
Докажите справедливость первого закона Моргана , используя таблицы истинности.
Докажите справедливость второго

закона Моргана , используя таблицы истинности.


















 Триггеры в презентации. Применение
Триггеры в презентации. Применение Презентация на тему Архиватор
Презентация на тему Архиватор  Школа::Кода Основы программирования на языке Python. 5 занятие
Школа::Кода Основы программирования на языке Python. 5 занятие Социальные сети на 01.08.18
Социальные сети на 01.08.18 Ивент по Batman: miniature game
Ивент по Batman: miniature game Интернет. Электронная почта
Интернет. Электронная почта Онлайн-школа IT Кулебяка. Проект
Онлайн-школа IT Кулебяка. Проект Всемирная паутина
Всемирная паутина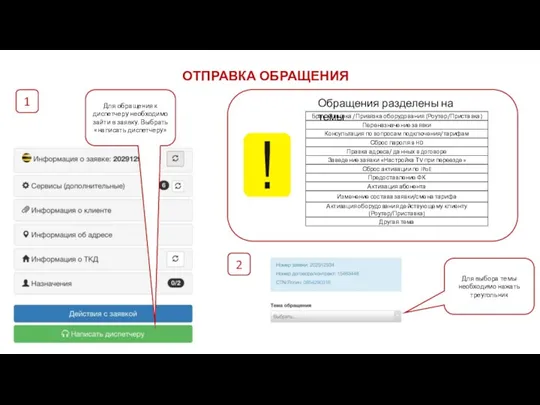 Отправка обращения
Отправка обращения Цвет
Цвет Угорзы Интернета
Угорзы Интернета Основные свойства JavaScript. Лабораторная работа №16
Основные свойства JavaScript. Лабораторная работа №16 The nature of the mass media and media literacy
The nature of the mass media and media literacy Кодирование информации в компьютере
Кодирование информации в компьютере Онлайн магазин Avon
Онлайн магазин Avon Osnovnye_ponyatia_i_klassifikatsia_BD
Osnovnye_ponyatia_i_klassifikatsia_BD Сайты помощники в изучении английского языка
Сайты помощники в изучении английского языка Коммуникация. Принципы связи
Коммуникация. Принципы связи Patents Power. Конкурс на лучшие биотехнологические стартапы
Patents Power. Конкурс на лучшие биотехнологические стартапы 10u-2b_СистемыСчисления
10u-2b_СистемыСчисления How it+ differs from ++i
How it+ differs from ++i Условный оператор в языке C#
Условный оператор в языке C# Bondder Landing page-Scroll down script
Bondder Landing page-Scroll down script Марафон “5 дней - 5 навыков”. Востребованные навыки в удаленной профессии
Марафон “5 дней - 5 навыков”. Востребованные навыки в удаленной профессии ЦМТ схемы
ЦМТ схемы Осмотр компьютера
Осмотр компьютера Тестовая программа по информатике
Тестовая программа по информатике Навигация. Иерахическая навигация. Xamarin Forms
Навигация. Иерахическая навигация. Xamarin Forms