Содержание
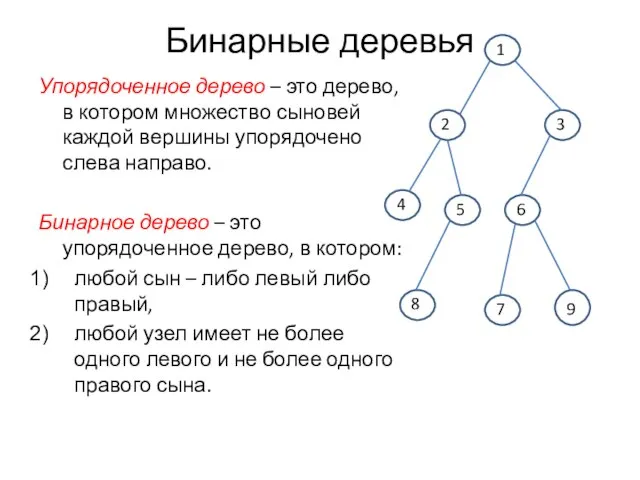
- 2. Бинарные деревья Упорядоченное дерево – это дерево, в котором множество сыновей каждой вершины упорядочено слева направо.
- 3. Обходы деревьев в глубину Пусть T – дерево, r- корень, v1, v2,…, vn – сыновья вершины
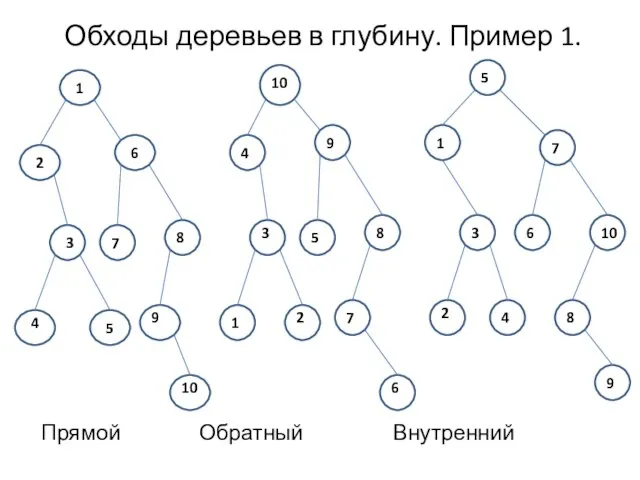
- 4. Обходы деревьев в глубину. Пример 1. Прямой Обратный Внутренний 1 2 6 3 7 8 4
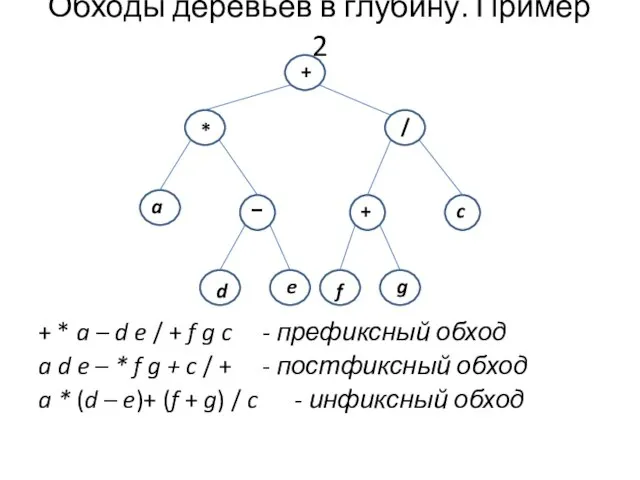
- 5. Обходы деревьев в глубину. Пример 2 + * a – d e / + f g
- 6. Реализация обхода typedef struct node { char * word; struct node * left; struct node *
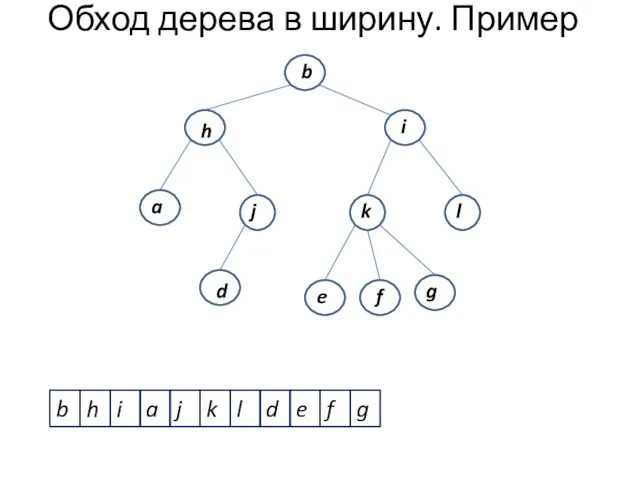
- 7. Обход дерева в ширину - это обход вершин дерева по уровням, начиная от корня, слева направо
- 8. Обход дерева в ширину. Пример b h i j k l d e f a g
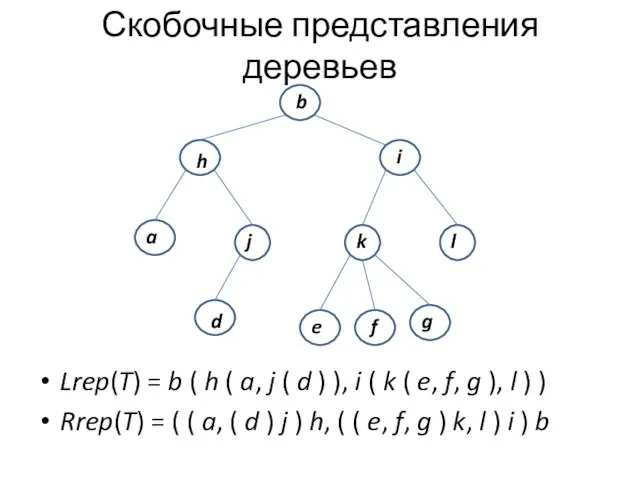
- 9. Представления деревьев Определение. Левое скобочное представление дерева Т (обозначается Lrep(Т)) можно получить, применяя к нему следующие
- 10. Скобочные представления деревьев Lrep(T) = b ( h ( a, j ( d ) ), i
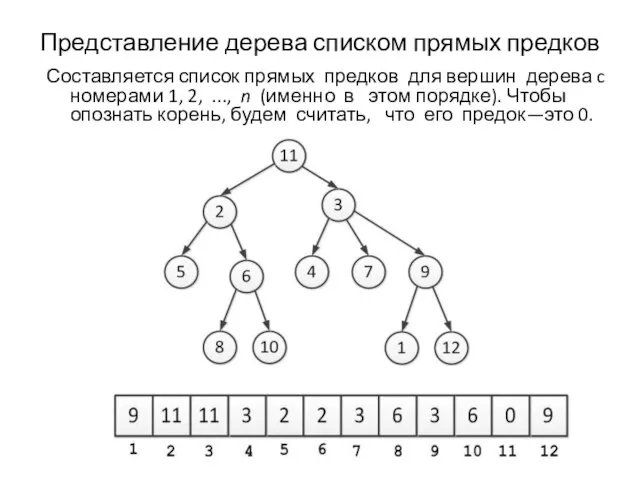
- 11. Представление дерева списком прямых предков Составляется список прямых предков для вершин дерева c номерами 1, 2,
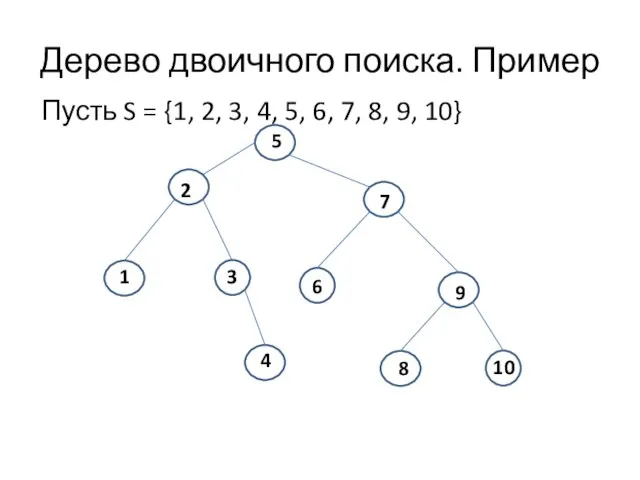
- 12. Дерево двоичного поиска Определение. Деревом двоичного поиска для множества S называется помеченное двоичное дерево, каждый узел
- 13. Дерево двоичного поиска. Пример Пусть S = {1, 2, 3, 4, 5, 6, 7, 8, 9,
- 14. Алгоритм просмотра дерева двоичного поиска Вход: Дерево T двоичного поиска для множества S, элемент a. Выход:
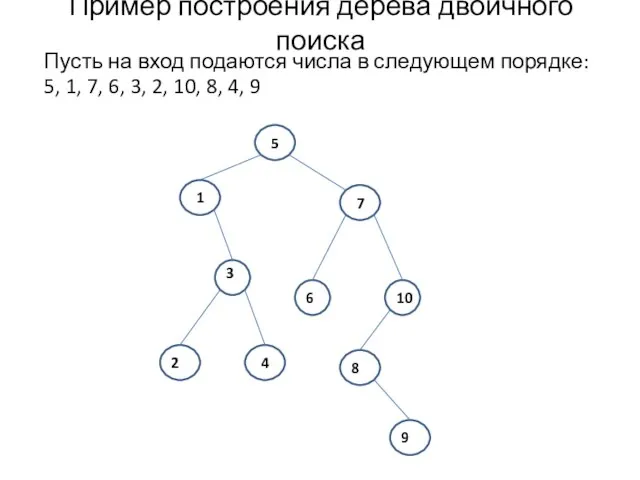
- 15. Пример построения дерева двоичного поиска Пусть на вход подаются числа в следующем порядке: 5, 1, 7,
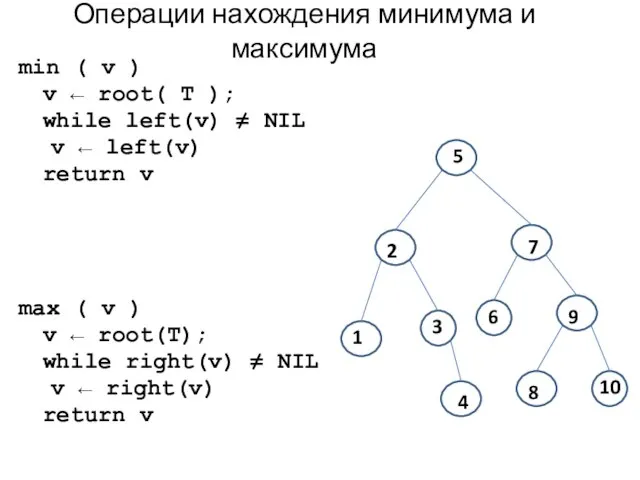
- 16. Операции нахождения минимума и максимума min ( v ) v ← root( T ); while left(v)
- 17. Операция поиска следующего successor (x) if right[x] ≠ NIL then return min (right [x]) y ←
- 18. Операция удаления элемента из дерева поиска Delete(T, z) if left[z] = NIL or right[z] = NIL
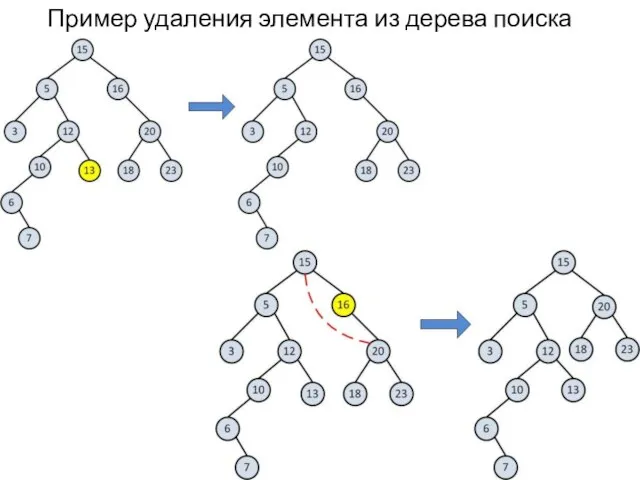
- 19. Пример удаления элемента из дерева поиска
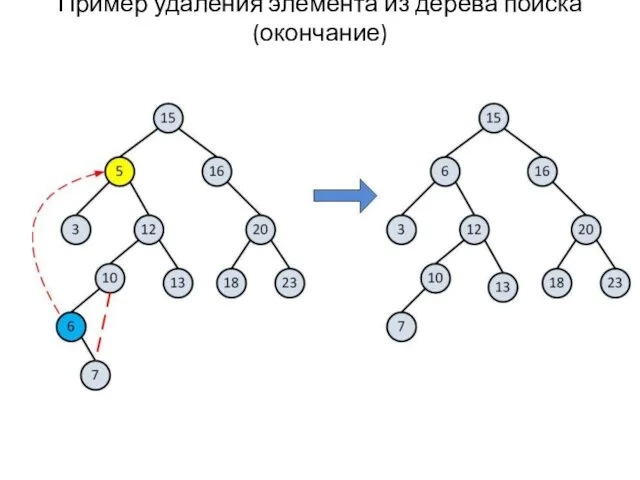
- 20. Пример удаления элемента из дерева поиска (окончание)
- 21. Теорема (Т. Кормен и др.) Математическое ожидание высоты случайного бинарного дерева поиска с n ключами равно
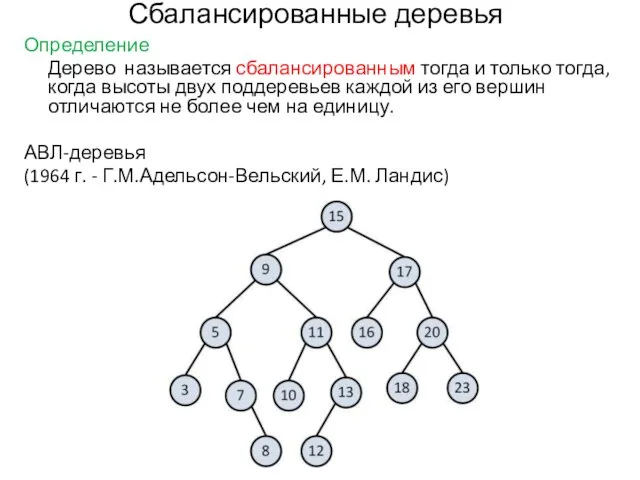
- 22. Сбалансированные деревья Определение Дерево называется сбалансированным тогда и только тогда, когда высоты двух поддеревьев каждой из
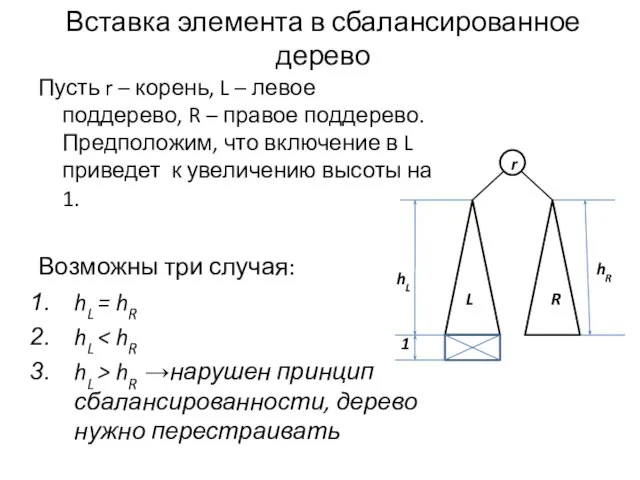
- 23. Вставка элемента в сбалансированное дерево Пусть r – корень, L – левое поддерево, R – правое
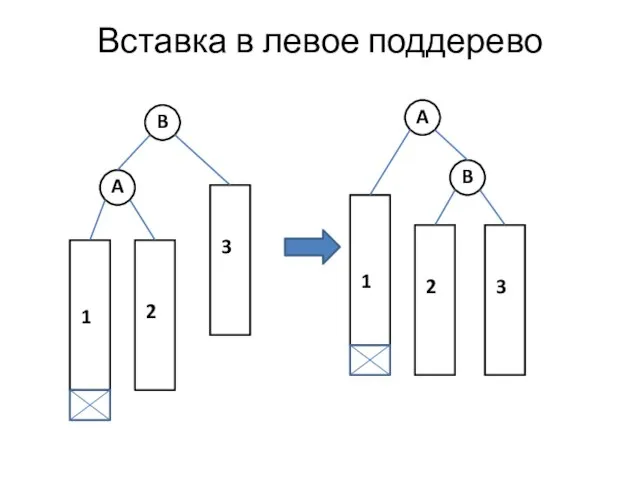
- 24. Вставка в левое поддерево A B 3 2 1 A B 3 2 1
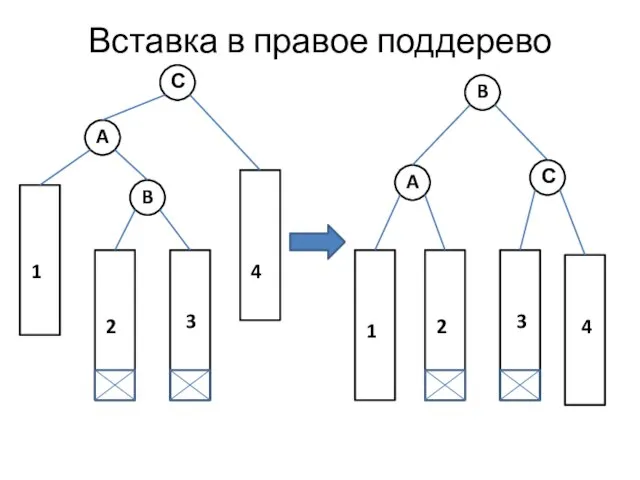
- 25. Вставка в правое поддерево A B 3 2 1 С 4 A 3 2 1 С
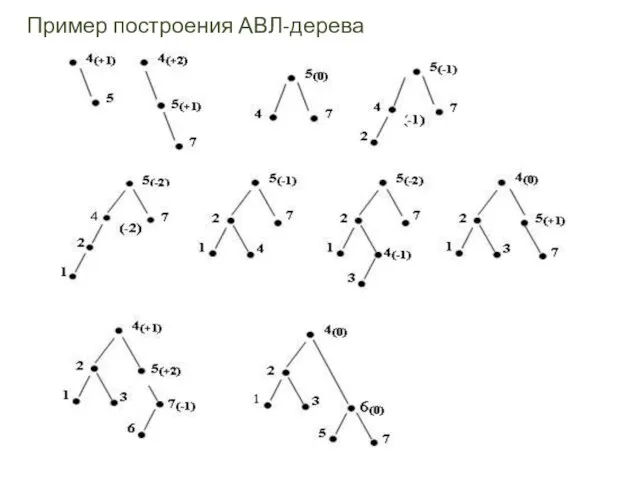
- 26. Пример построения АВЛ-дерева
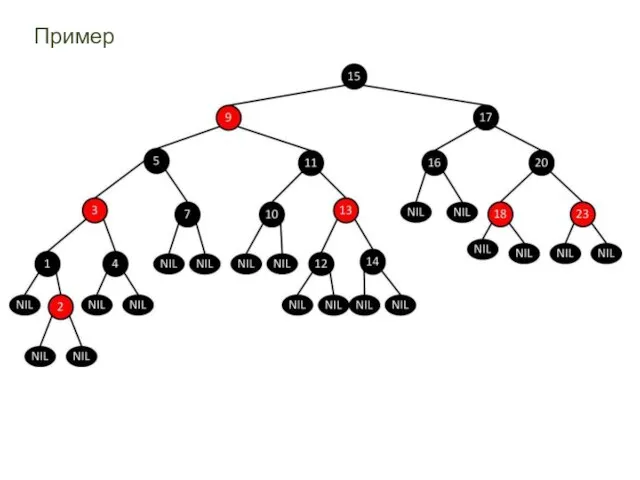
- 27. Красно-чёрное дерево (Red-Black-Tree, RB-Tree) Красно-чёрное дерево обладает следующими свойствами. Каждый узел либо красный либо чёрный Все
- 28. Пример
- 29. Свойства красно-чёрного дерева 1. Если h - чёрная высота дерева, то количество листьев не менее 2h
- 30. Повороты Left_Rotate(T, x) y ← right[x] right[x] ← left[y] if left[y] ≠ nil [T] then p[left[y]]
- 31. Операция вставки Чтобы вставить узел, мы сначала ищем в дереве место, куда его следует добавить. Новый
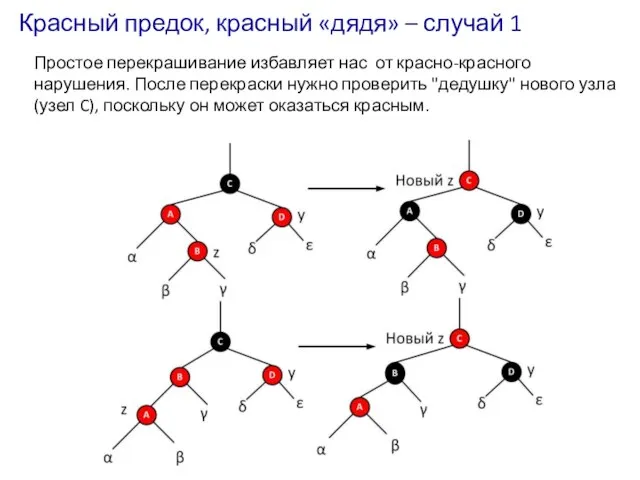
- 32. Красный предок, красный «дядя» – случай 1 Простое перекрашивание избавляет нас от красно-красного нарушения. После перекраски
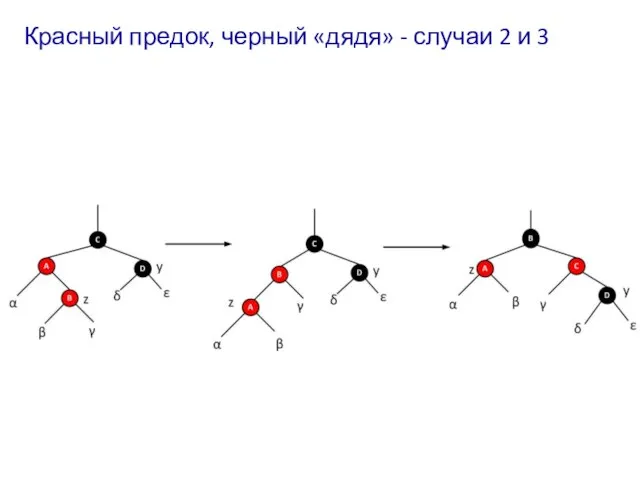
- 33. Красный предок, черный «дядя» - случаи 2 и 3
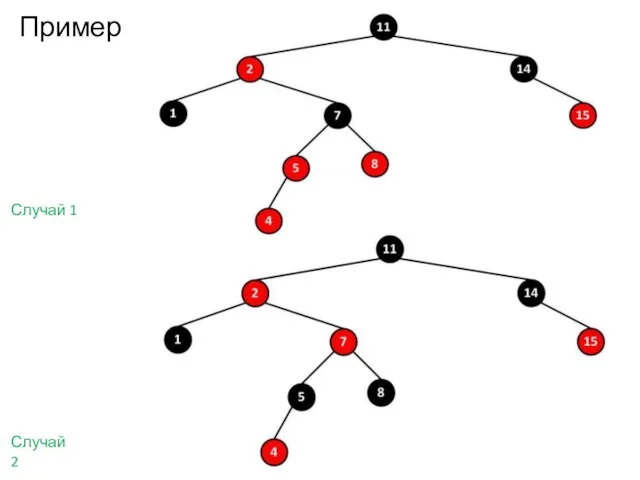
- 34. Пример Случай 1 Случай 2
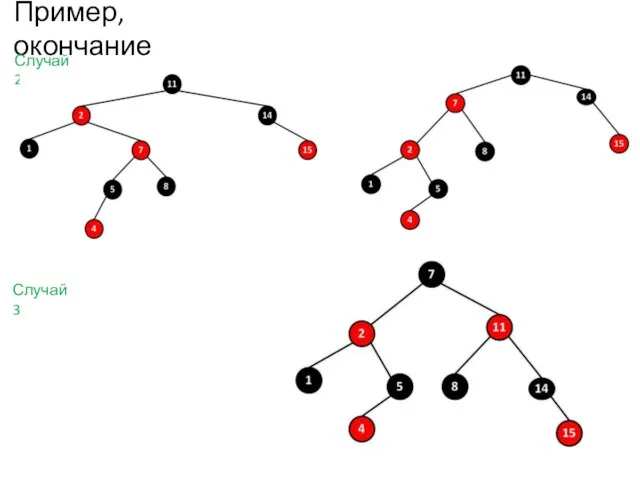
- 35. Пример, окончание Случай 2 Случай 3
- 36. Удаление узла Если удаляемый узел красный все правила сохраняются и все прекрасно. Если же удаляемый узел
- 37. Сравнение с АВЛ-деревом Пусть высота дерева h, минимальное количество листьев N. Тогда: для АВЛ-дерева N(h) =
- 38. Поиск, вставка, удаление Поиск. Поскольку красно-чёрное дерево, в худшем случае, выше, поиск в нём медленнее, но
- 39. Splay деревья Сплей-дерево (Splay-tree) — это двоичное дерево поиска. Оно позволяет находить быстрее те данные, которые
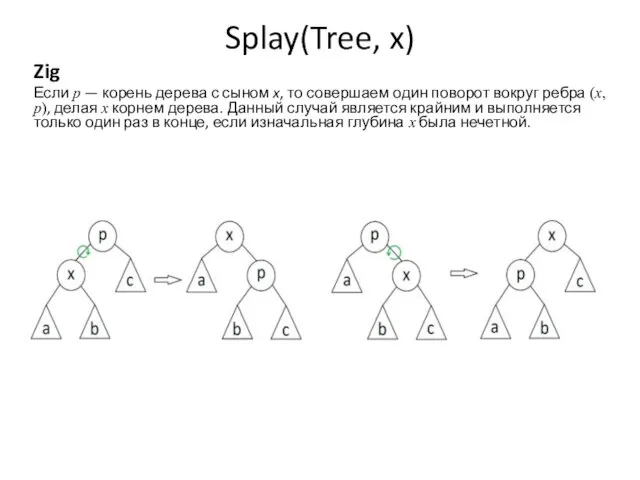
- 40. Splay(Tree, x) Zig Если p — корень дерева с сыном x, то совершаем один поворот вокруг
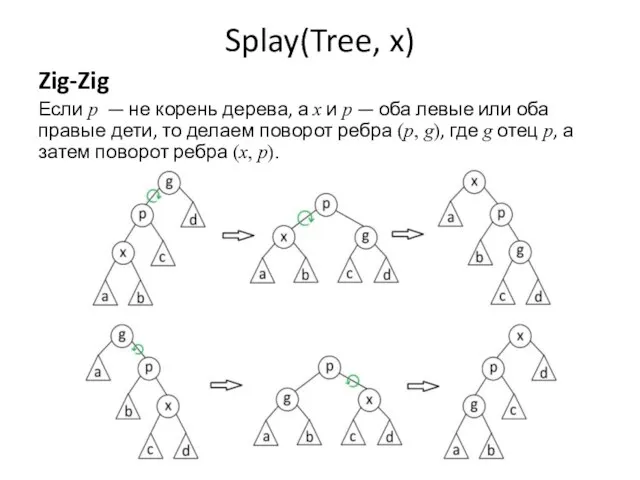
- 41. Splay(Tree, x) Zig-Zig Если p — не корень дерева, а x и p — оба левые
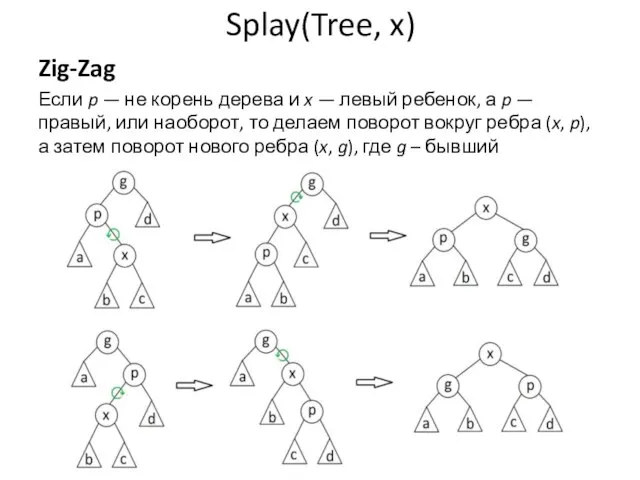
- 42. Splay(Tree, x) Zig-Zag Если p — не корень дерева и x — левый ребенок, а p
- 43. Операции Find (Tree, x) Эта операция выполняется как для обычного бинарного дерева, только после нее запускается
- 44. Анализ Splay Амортизационный анализ сплей-дерева проводится с помощью метода потенциалов. Потенциалом рассматриваемого дерева назовём сумму рангов
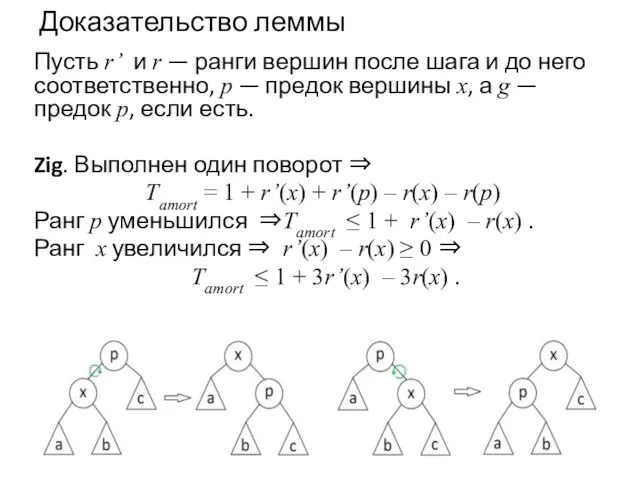
- 45. Доказательство леммы Пусть r’ и r — ранги вершин после шага и до него соответственно, p
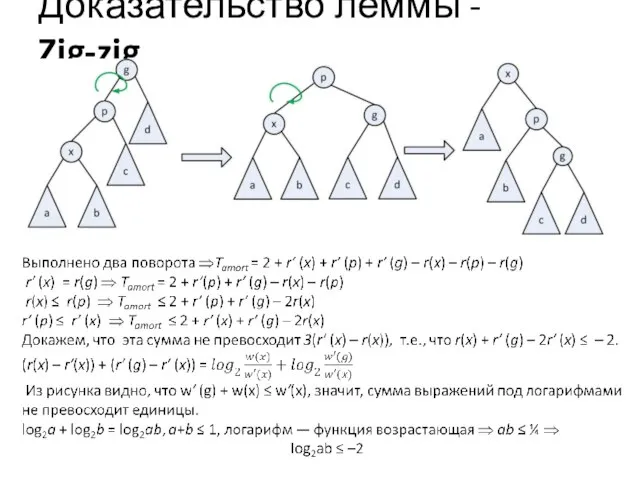
- 46. Доказательство леммы - Zig-zig.
- 48. Скачать презентацию






![Операция поиска следующего successor (x) if right[x] ≠ NIL then return min](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/881427/slide-16.jpg)
![Операция удаления элемента из дерева поиска Delete(T, z) if left[z] = NIL](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/881427/slide-17.jpg)



![Повороты Left_Rotate(T, x) y ← right[x] right[x] ← left[y] if left[y] ≠](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/881427/slide-29.jpg)







 Подготовили Батуева Л.Н.-учитель математики МБОУ СОШ №11 г.Чайковский , Маркова Е.В- учитель информатики МБОУ СОШ №11 г.Чайковск
Подготовили Батуева Л.Н.-учитель математики МБОУ СОШ №11 г.Чайковский , Маркова Е.В- учитель информатики МБОУ СОШ №11 г.Чайковск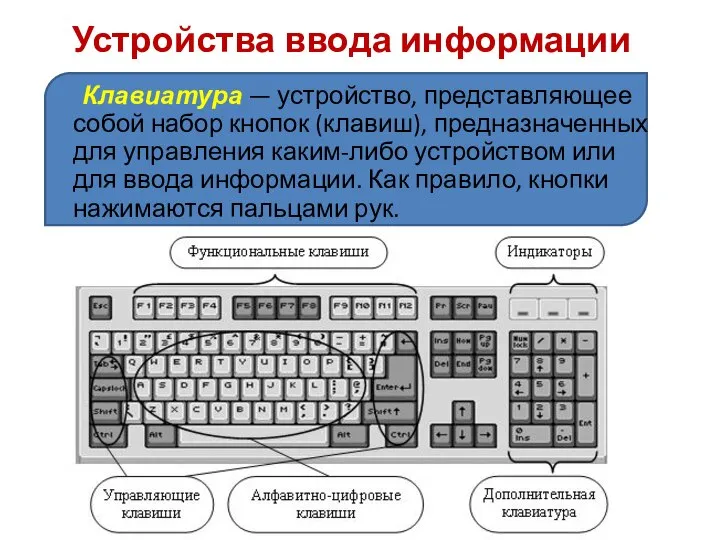 Устройства ввода информации
Устройства ввода информации Обои для презентации
Обои для презентации Readsee/Ридси. Читай и вдохновляйся
Readsee/Ридси. Читай и вдохновляйся Исследование подходов для аутентификации пользователей беспроводной сети с применением различных LDAP решений
Исследование подходов для аутентификации пользователей беспроводной сети с применением различных LDAP решений Математические основы информатики. Общие сведения о системах счисления
Математические основы информатики. Общие сведения о системах счисления 0821dd87747943779db6c0c7e5802e37
0821dd87747943779db6c0c7e5802e37 Безопасность детей в Интернете
Безопасность детей в Интернете Digital Paper. Цифровая бумага. Новый цифровой носитель информации
Digital Paper. Цифровая бумага. Новый цифровой носитель информации Технические средства обучения
Технические средства обучения Логические основы ЭВМ
Логические основы ЭВМ Визуальная среда математического моделирования MathCAD
Визуальная среда математического моделирования MathCAD Компьютерные технологии в спорте
Компьютерные технологии в спорте Системы счисления
Системы счисления Цветовая модель RGB
Цветовая модель RGB Как не убить канал YouTube рекламой и почему она эффективна
Как не убить канал YouTube рекламой и почему она эффективна Моделирование и формализация
Моделирование и формализация Моя жизнь на Amazing RP
Моя жизнь на Amazing RP Сервісні програми ОС
Сервісні програми ОС Надстройка Пакет анализа в Excel
Надстройка Пакет анализа в Excel Представление графов. Топологическая сортировка
Представление графов. Топологическая сортировка Объект и его свойства
Объект и его свойства Проектирование. Диаграммы
Проектирование. Диаграммы Ввод и редактирование данных в редакторе Excel
Ввод и редактирование данных в редакторе Excel Информация и её свойства. Информация и информационные процессы
Информация и её свойства. Информация и информационные процессы Операторы условия, цикла, функции
Операторы условия, цикла, функции Обработка символьной информации в языке Pascal
Обработка символьной информации в языке Pascal Паскаль. Циклические вычисления
Паскаль. Циклические вычисления