Содержание
- 2. Для каждой л.р. есть: методические указания (файл - docx); дополнительный (теоретический) материал (файл - pptx); пример
- 3. Любая цифровая вычислительная система обязательно включает в себя, по крайней мере, один цифровой процессор, который является
- 4. Арифметические основы цифровых процессоров
- 5. Содержание лекции 1: Системы счисления, используемые при работе с цифровыми процессорами и способы перевода Форматы представления
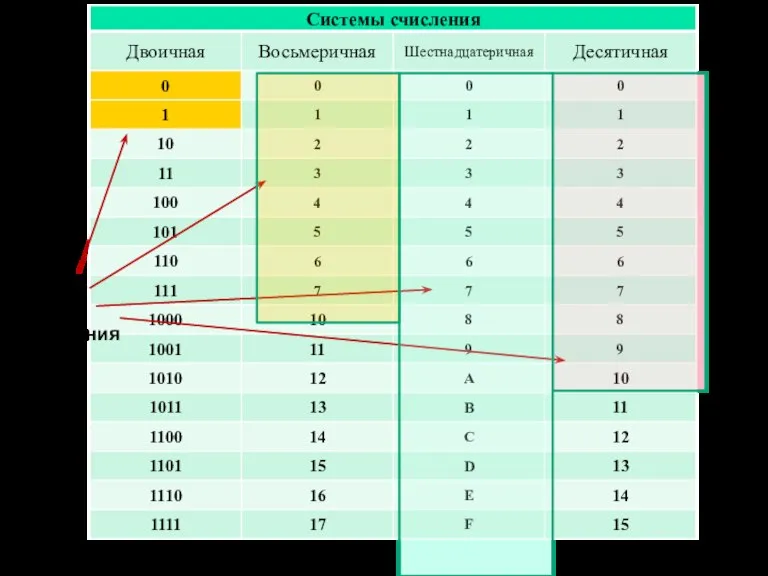
- 6. Системы счисления, используемые при работе с цифровыми процессорами и способы перевода
- 7. Информация, которую обрабатывает цифровой процессор хранится в оперативной памяти и в его регистрах. Эта информация кодируется.
- 8. Большинство кодов, применяемых в цифровых процессорах, основано на системах счисления, использующих позиционный принцип образования числа, при
- 9. При работе с цифровыми процессорами используются четыре позиционные системы счисления. двоичная – представление информации (в памяти,
- 10. Каждая позиционная система счисления имеет базу. База системы счисления это количество символов, используемых в ней. В
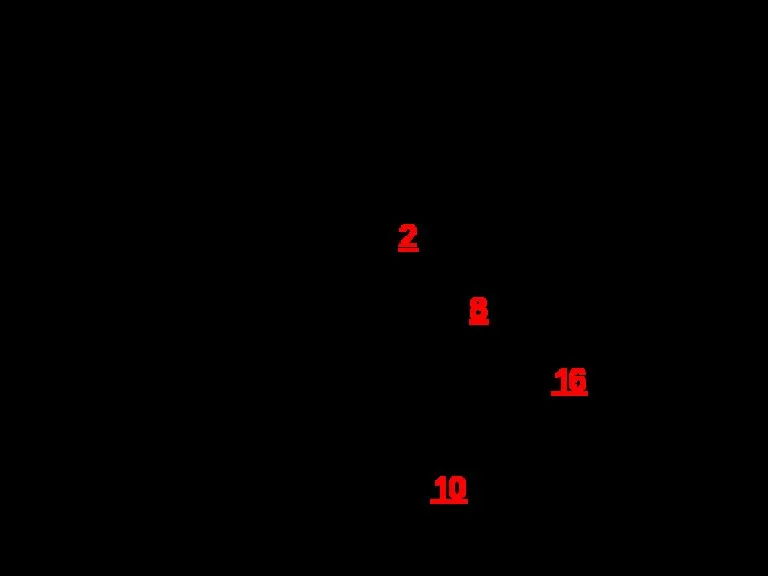
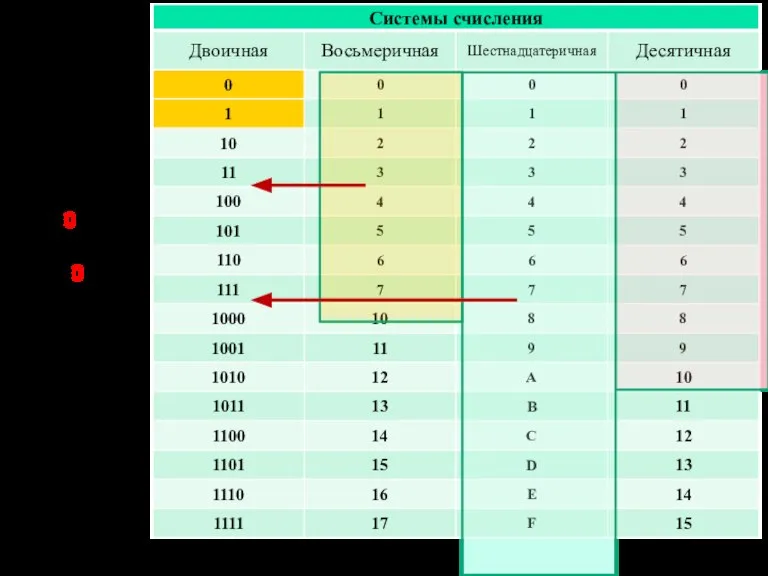
- 11. Базы систем счисления
- 12. В IT-литературе используются следующие обозначения, чтобы указать систему счисления, в которой представлены числа: для двоичной системы:
- 13. для восьмеричной системы: нижний индекс справа от числа в виде цифры 8 в скобках или букв
- 14. для шестнадцатеричной системы: нижний индекс справа от числа в виде числа 16 в скобках или букв
- 15. Перевод чисел Рассмотрим алгоритмы перевода чисел из одной системы счисления в другую. Эти алгоритмы различаются в
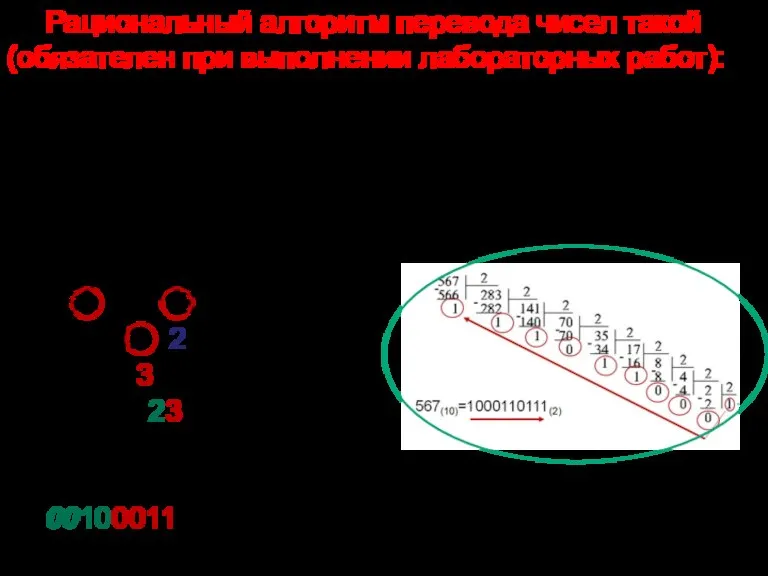
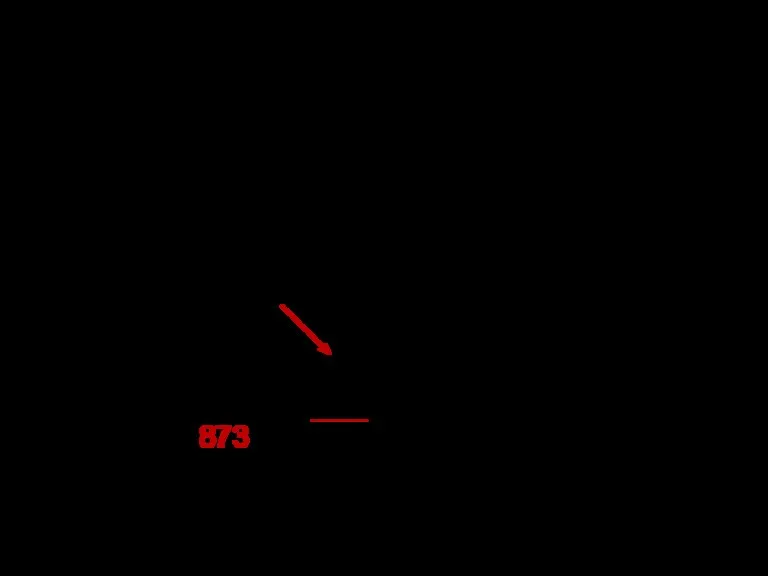
- 16. Алгоритм перевода целых чисел Перевести число 567 из десятичной в двоичную систему. 567(10)=1000110111(2) Внимание: не переводить
- 17. Почему используются 8-чная и 16-чная системы? При переводе из десятичной (или же в десятичную) системы счисления
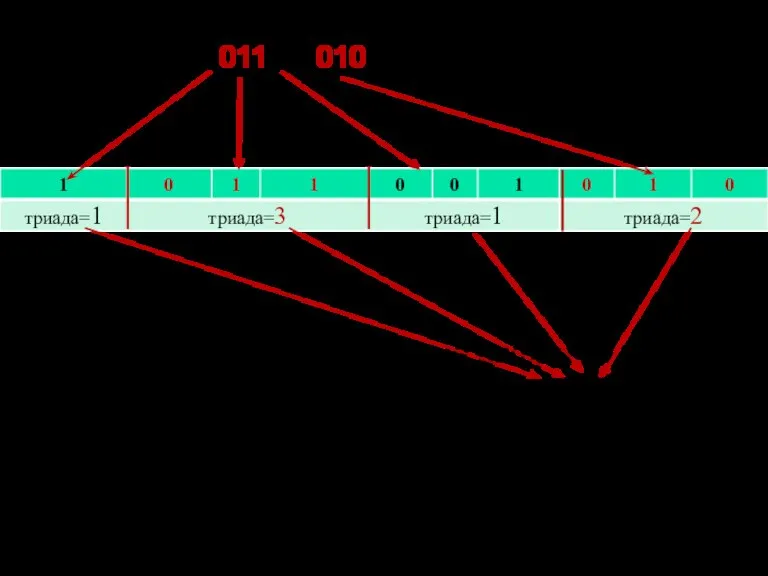
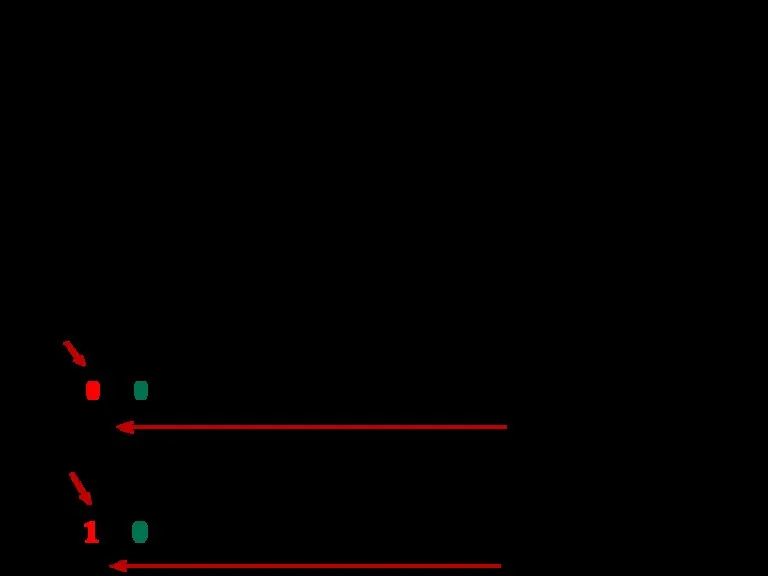
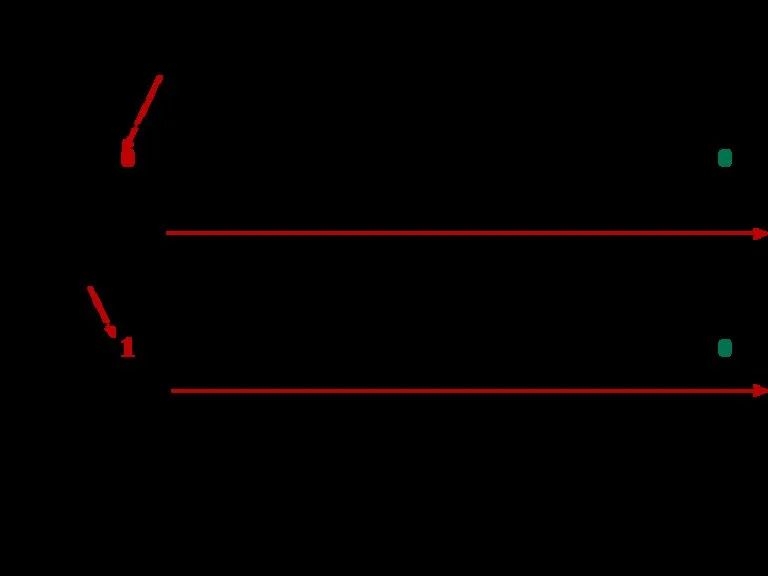
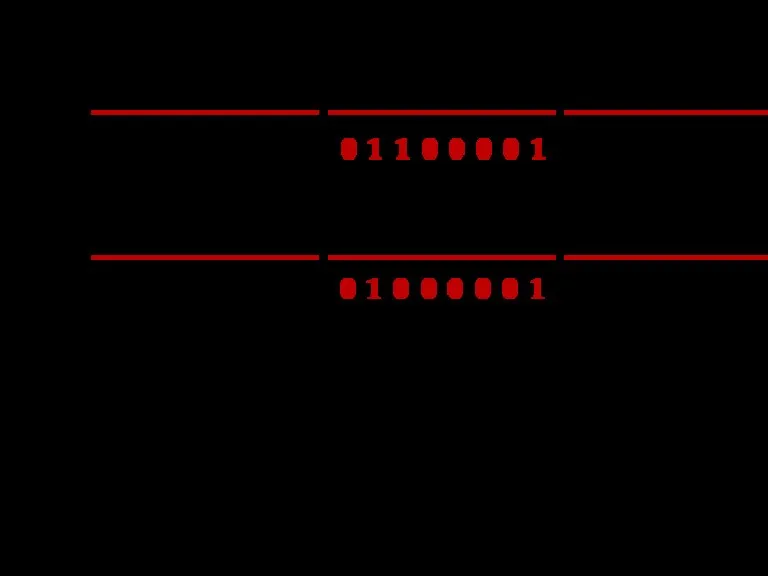
- 18. Перевод из 8,16-чной в 2-чную Для того чтобы целое двоичное число перевести из системы счисления с
- 19. 3(8)=011(2) 7(16)=0111(2)
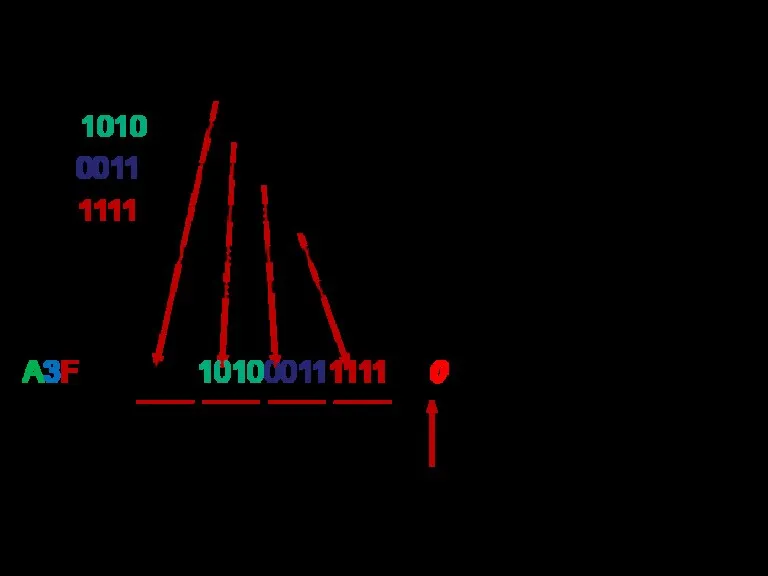
- 20. Перевести 4A3F(16) в двоичную систему счисления: 4(16)=0100(2) – тетрада; A(16)=1010(2) – тетрада; 3(16)=0011(2) – тетрада; F(16)=1111(2)
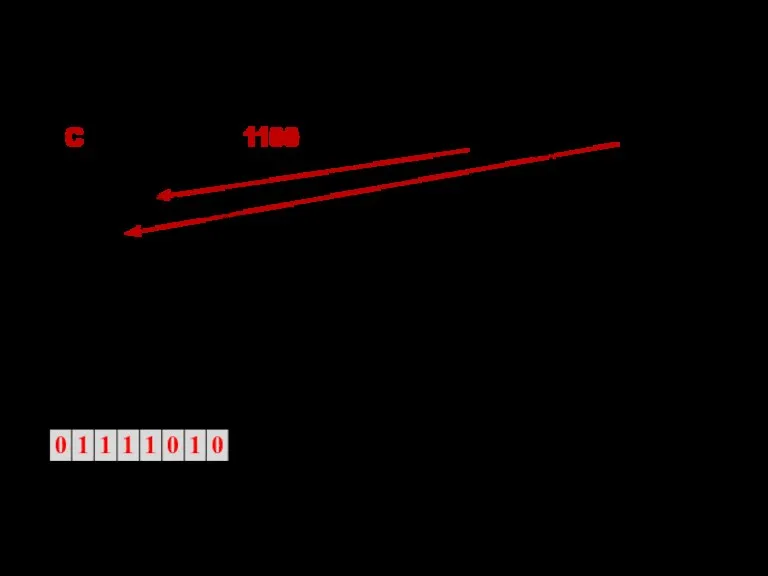
- 21. Перевод из 2-чной в 8, 16-чную: для того чтобы целое двоичное число перевести в систему счисления
- 22. Перевести 1011001010(2) в восьмеричную систему счисления: Тогда, располагая восьмеричные цифры по весам разрядов, получаем: 1010001010(2)=1312(8)
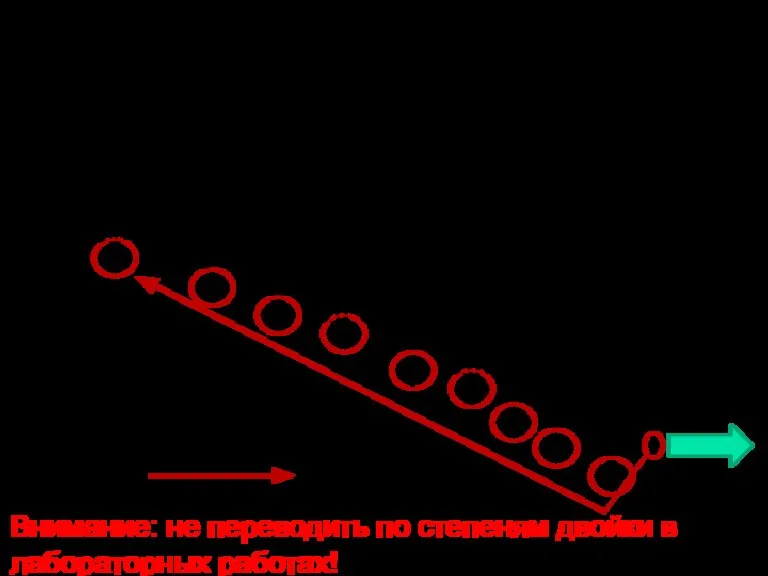
- 23. Рациональный алгоритм перевода чисел такой (обязателен при выполнении лабораторных работ): от человека к процессору --- 10
- 24. Правильная дробь имеет целую часть, равную 0. Перевод дроби в другую систему счисления выполняется по следующему
- 25. полученная целая часть произведения отбрасывается, и оставшаяся дробная часть (это правильная дробь) вновь умножается на основание
- 26. Внимание! Если целые числа из одной системы счисления в другую всегда переводятся точно, то дробные числа,
- 27. Если надо получить три точных разряда, то при переводе получают четыре разряда и последний четвертый разряд
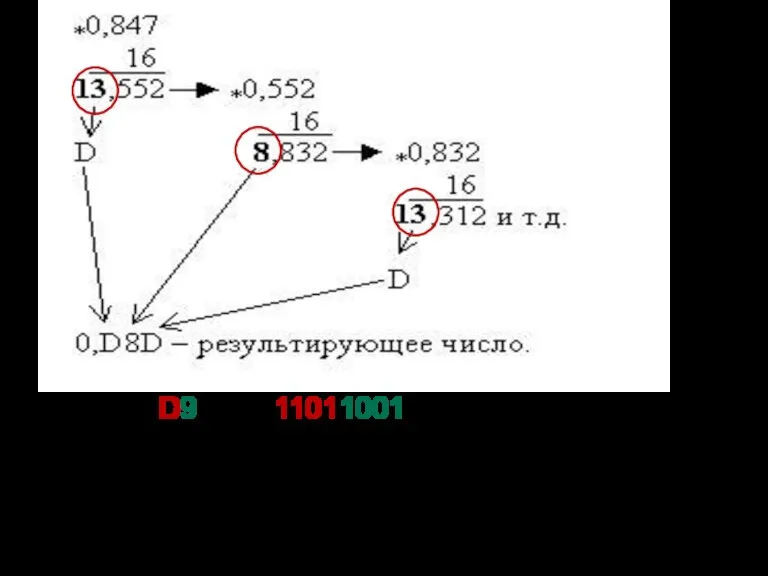
- 28. Пример перевода правильной дроби: Выполнить перевод числа 0,847(10) в двоичную систему счисления. Перевод выполнить с точностью
- 29. 0,847(10)≈0,D9(16)=0,11011001(2). Отметим, что третья шестнадцатеричная цифра после запятой использована для округления предыдущего разряда (второй после запятой)
- 30. Перевод дроби из 2-чной системы в 10-чную: Выполнить перевод правильной дроби 0,001111011010001(2) в десятичную систему счисления.
- 32. Форматы представления чисел в цифровых процессорах
- 33. Цифровой процессор – это устройство, осуществляющее обработку информации, представленной в цифровом виде (двоичная система счисления). Внешне
- 34. Т.е. разрядность процессора определяет сколько бит используются для выполнения операций сложения, вычитания, сдвига или других команд
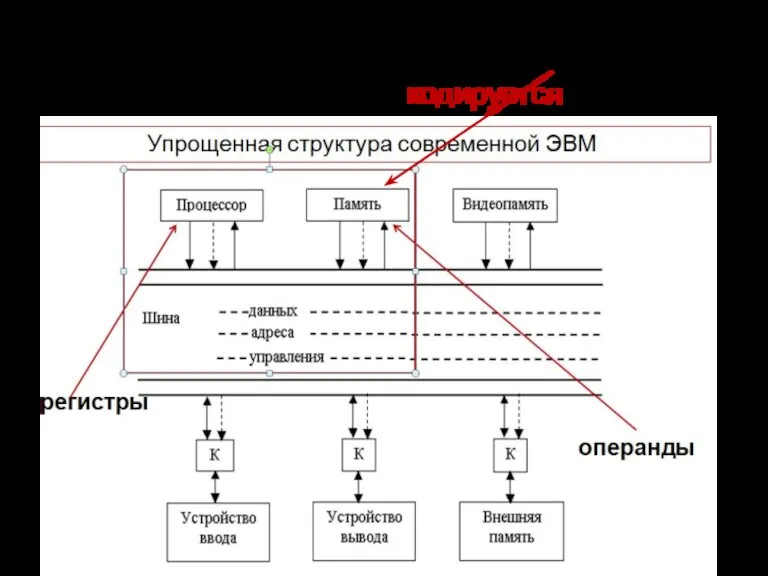
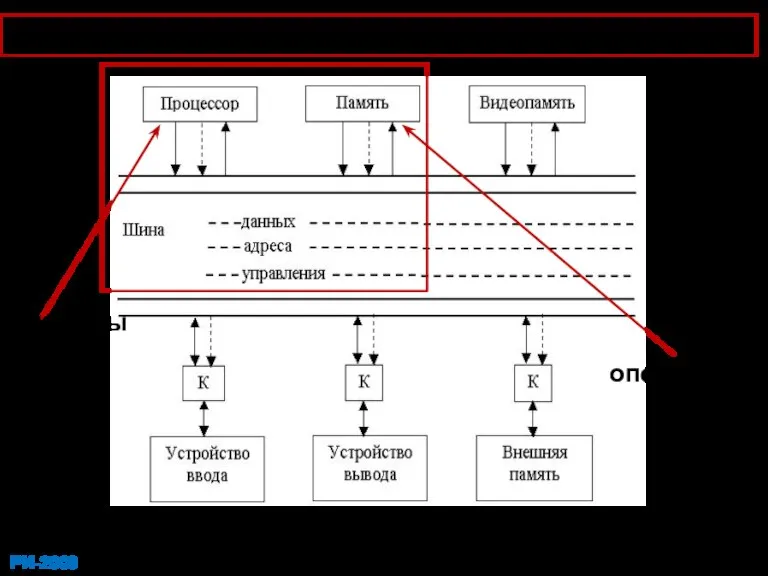
- 35. (ОЗУ) Упрощенная структура современной ЭВМ регистры операнды
- 36. В цифровом процессоре для представления чисел используются три следующих формата : формат с фиксированной точкой; формат
- 37. Формат с фиксированной точкой (sign, unsign) Формат с фиксированной точкой (ФТ), в зависимости от представляемых чисел,
- 38. Формат ФТ (sign) представления целых чисел Целое число К1, заданное в восьмеричной системе счисления, представить в
- 39. Еще пример для целого числа: Целое число К2, заданное в восьмеричной системе счисления, представить в формате
- 40. Формат представления правильных дробей Дробное число М1, заданное в восьмеричной системе счисления, представить в формате с
- 41. Дробное число М2, заданное в восьмеричной системе счисления, представить в формате с ФТ в 8-разрядном процессоре
- 42. Смешанные числа (неправильные дроби) Для представления таких чисел в формате с ФТ разрядная сетка процессора делится
- 44. В формате ФТ (целые, дробные, смешанные) арифметические операции выполняются точно. Диапазон вычисления с ФТ определяется разрядностью
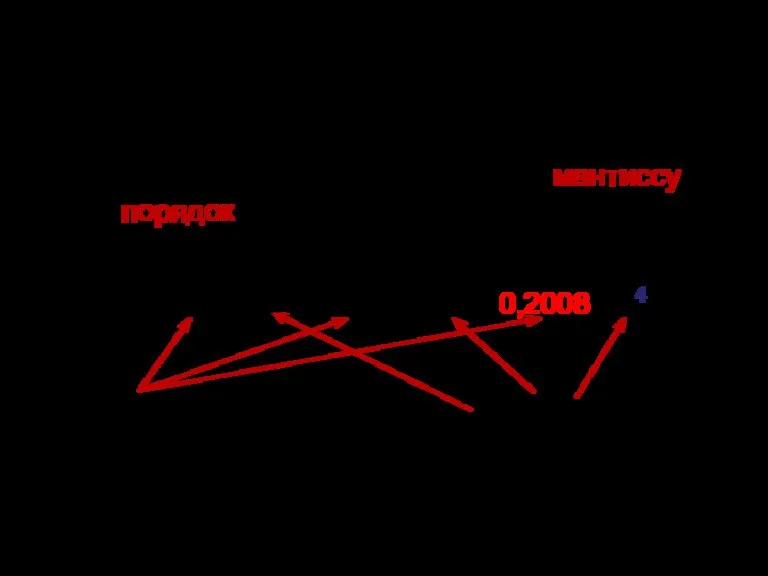
- 45. Формат с плавающей точкой (float) Одной из форм записи вещественных чисел является их представление в экспоненциальном
- 46. Любое число в экспоненциальной форме имеет множество представлений. 1=0,00001*105=1000*10-3 и т.д. Среди этих представлений выделили нормализованное
- 47. Операнды в цифровом процессоре в формате с плавающей точкой (ПТ/float) представляют числа в экспоненциальной форме. Такой
- 48. В истории IT- технологий существовало много форматов чисел в формате с ПТ. В настоящее время общепринятым
- 49. Смещение порядка на константу позволяет обойтись без явного бита знака порядка. Если значение смещенного порядка больше
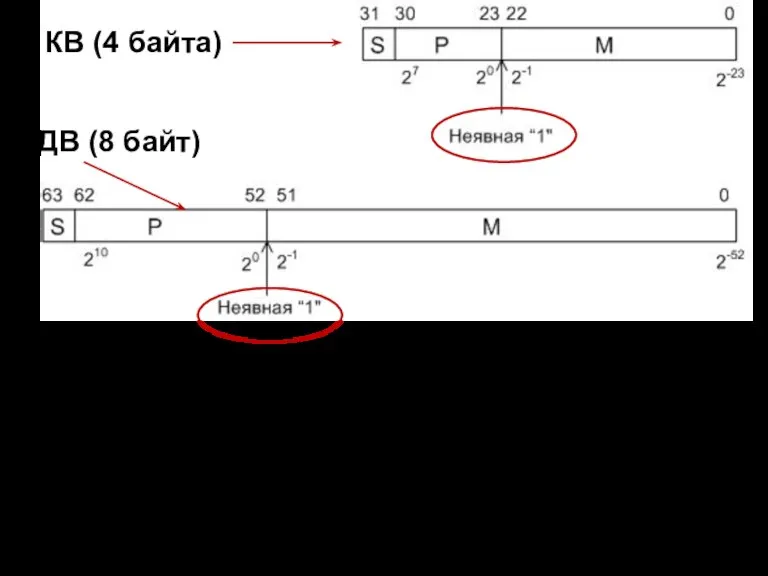
- 50. Есть два формата представления чисел с плавающей точкой стандарта IEEE 754 в оперативной памяти процессора :
- 51. Используются следующие обозначения: М – мантисса числа; S – знак мантиссы; Р – порядок числа. В
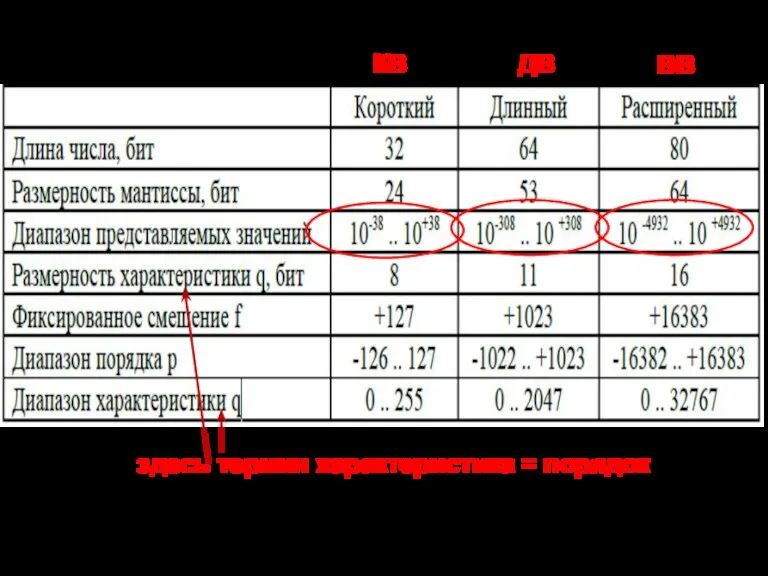
- 52. Форматы вещественных чисел в IEEE-754 КВ ДВ ВВ здесь термин характеристика = порядок
- 53. «Скрытый» бит мантиссы Поскольку при нормализованном представлении операнда (0,1(2)≤ М это можно использовать для увеличения диапазона
- 54. Алгоритм преобразования вещественного десятичного числа в двоичное число с плавающей точкой формата IEEE 754 ( на
- 55. 3. Записать полученное значение дробной части после десятичной точки. Если количество разрядов мантиссы получилось меньше выделенного
- 56. 5. Нормализовать полученное двоичное число (1(2)≤М 1,0000010000000000000000000000000*1011 6. К порядку прибавить смещение в соответствии с форматом,
- 57. 7. Записать значение порядка и значение мантиссы в соответствующие биты формата КВ или ДВ (у мантиссы,
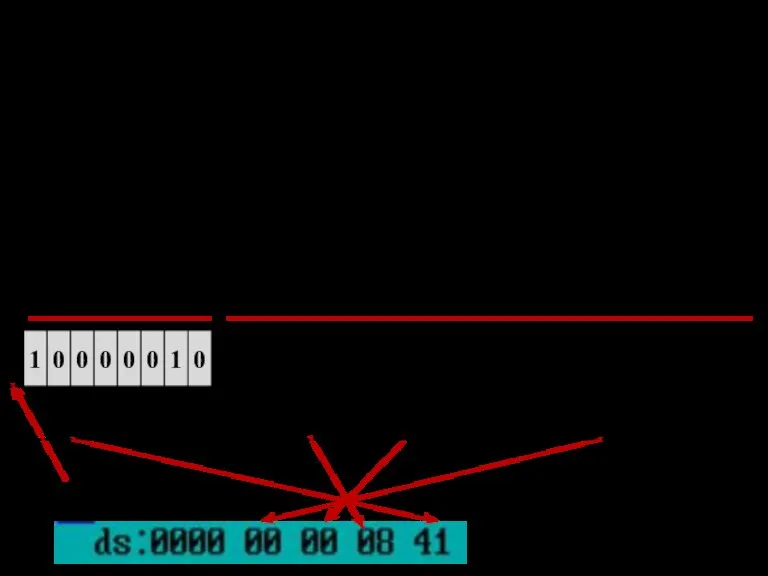
- 58. Рассмотрим другие примеры представления операндов в формате КВ. Напоминание: мантисса – М (1(2)≤М порядок – Р
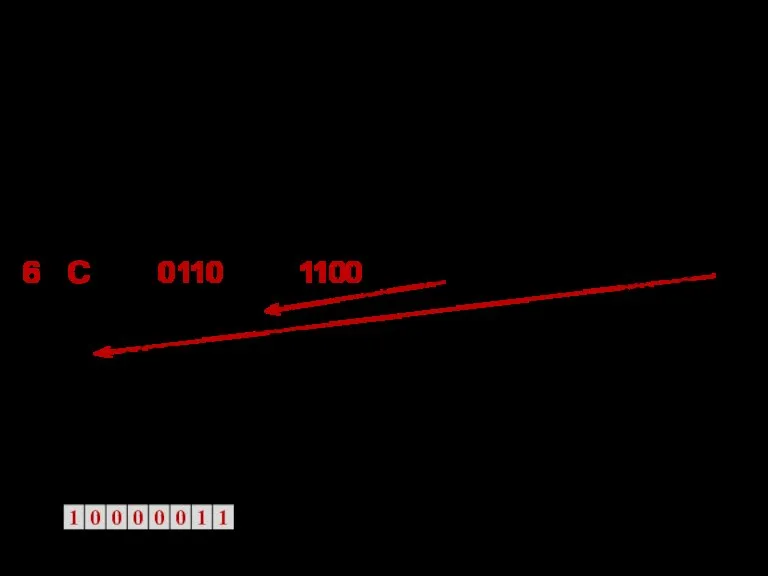
- 59. Еще пример: Представить число – 7,С8(16) в формате КВ. Перевод: –7,С8(16)= –111,11001000(2)= –1,1111001000(2)*1010. М= – 1,1111001000(2);
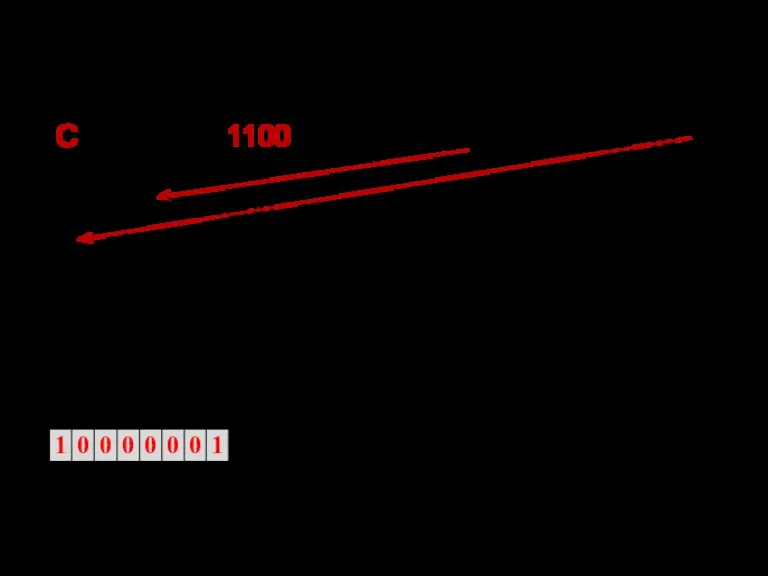
- 60. Еще пример: Представить число – 0,0С8(16) в формате КВ. Перевод: –0,0С8(16)= –0,000011001000(2)= –1,1001000(2)*10−101. М= – 1,1001000(2);
- 61. Специальные значения Несмотря на большой диапазон вещественных чисел, представимых в формате с ПТ, бесконечное количество чисел
- 62. К специальным значениям относятся: денормализованные вещественные числа, отрицательная и положительная бесконечности, не числа; неопределенности, значения в
- 63. Нуль Значение нуля относится к специальным. Это делается из-за того, что нуль выделяется среди корректных вещественных
- 64. Денормализованные вещественные числа Денормализованные числа – числа, значе- ние которых меньше минимально представимого в нормализованном виде
- 65. Именно эти числа и представляют собой денормализованные числа. Однако диапазон денормализованных чисел не безграничен и определяется
- 66. Бесконечности Среди причин, приводящих к формированию значения бесконечности, в первую очередь следует назвать переполнение и деление
- 67. Не числа К не числам относятся такие битовые последовательности, которые не совпадают ни с одним из
- 68. Формат двоично-десятичного кода (BCD - код) Формат двоично-десятичного кода (BCD – binary coded decimal) в компьютерах
- 69. В настоящее время общепринятым стандартом представления операндов в BCD коде является стандарт IEEE 754. В его
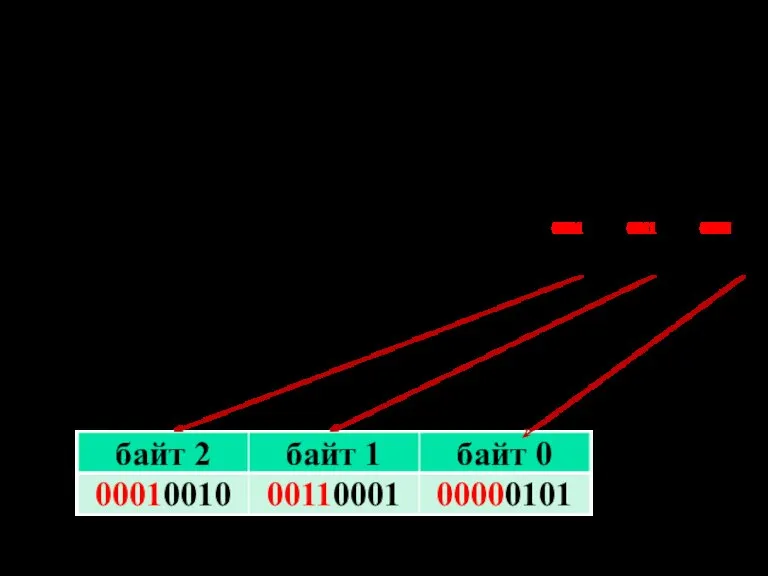
- 70. В соответствии со стандартом IEEE 754 под операнд отводится 10 байт, из них крайний левый байт
- 71. Пример: представить -1231,05(10) в BCD коде стандарта IEEE 754. – 00 00 00 00 00 00
- 72. Кодирование чисел в цифровых процессорах
- 73. Кодирование чисел в цифровых процессорах В цифровых процессорах в каждом из ранее рассмотренных форматов операнды представляются
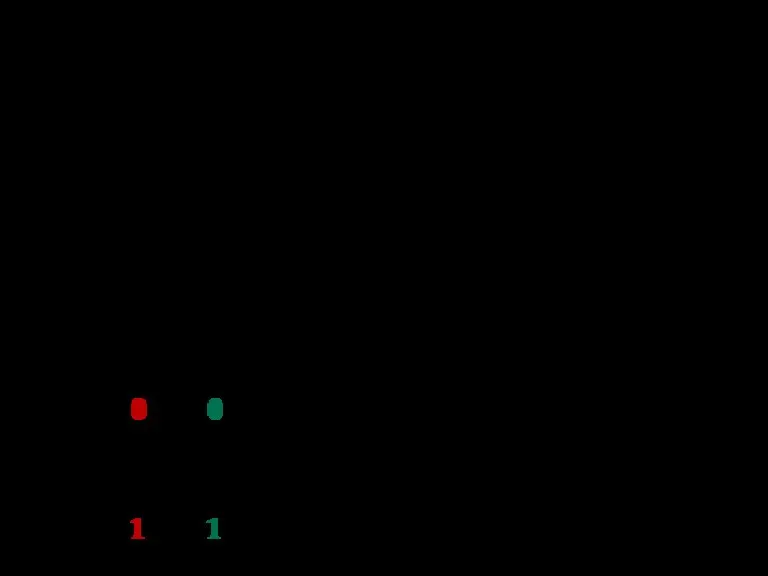
- 74. Прямой код Представление операнда в прямом коде состоит из двух частей: знака числа, под него отводится
- 75. М1=0,15(8)=+0,001101(2) М2= - 0,15(8)=+0,001101(2)
- 76. Достоинство прямого кода состоит в том, что в нем более просто реализуются алгоритмы выполнения «длинных» (по
- 77. Обратный код в настоящее время практически не используется. Обратный код положительного числа совпадает с самим числом,
- 78. Достоинствами обратного кода являются: знаковый и числовые биты операнда составляют единый код, поэтому просто реализуются алгоритмы
- 79. Дополнительный код Дополнительный код положительного числа совпадает с самим числом, представленным в заданном формате, а знаковый
- 80. Этот способ получения дополнительного кода следует из теории чисел. Например, для 16-разрядного процессора, который работает по
- 81. Дополнительный код (как и прямой и обратный) можно использовать в любой системе счисления. Рассмотрим пример использования
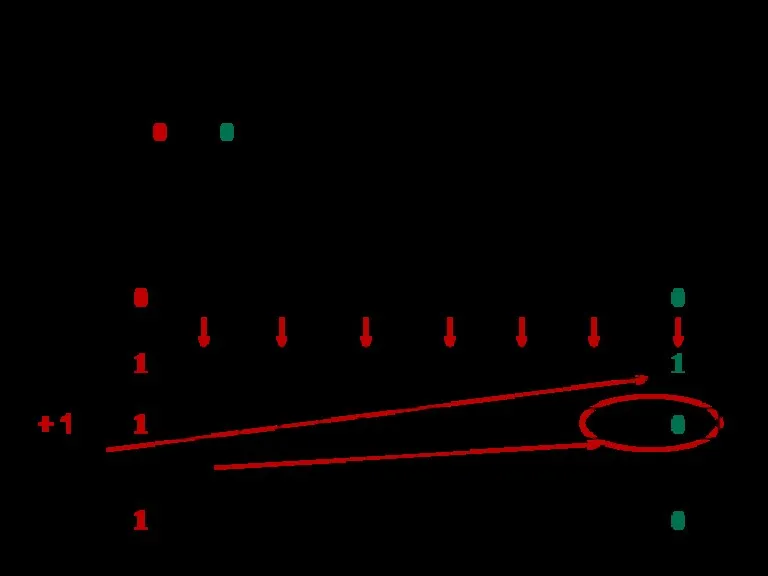
- 82. В цифровом процессоре, дополнительный код двоичного числа (с учетом формата представления) получается более простым способом. Алгоритм
- 83. По этому же алгоритму можно получить дополнительный код числа в любой системе счисления. Рассмотрим десятичную систему
- 84. Рассмотрим пример получения дополнительного кода в шестнадцатеричной системе счисления. Представить (- 6AF9(16)) в дополнительном коде. Дополняем
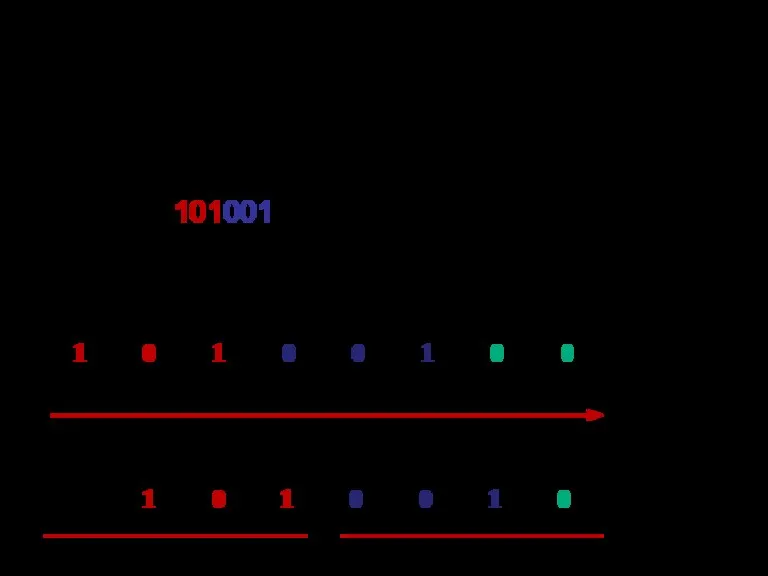
- 85. Примеры для 8-разрядного процессора: K1=51(8)=101001(2). --------------------------------------------------------------------------- M1= – 0,15(8)= –0,0011010(2) 01+1=10
- 86. L1=51,15(8)=101001,001101(2). ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- L2= – 51,15(8)= –101001,001101(2) целая часть дробная часть
- 87. Перевод числа из дополнительного кода Перевод в двоичную систему счисления из дополнительного кода выполняется (с учетом
- 88. L1=+101001,001101(2)=51,15(8) ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- L2= –101001,001101(2) = – 51,15(8)
- 89. Достоинство дополнительного кода в том, что знаковый и числовые биты операнда составляют единый код, а не
- 90. Несимметричный диапазон представления положительных и отрицательных чисел в цифровом процессоре в дополнительном коде приводит к тому,
- 91. Перевод в дополнительный код для минимально отрицательного числа (-1000…00) выполняется по следующему алгоритму: единица в знаковом
- 92. Например, для 8-разрядного процессора максимально представимые числа: максимальное положительное число равно 127(10)=177(8)=1111111(2) и его дополнительный код
- 93. Кодирование символьной информации Первые цифровые процессоры обрабатывали только числовые данные. Сейчас процессоры в большей степени обрабатывает
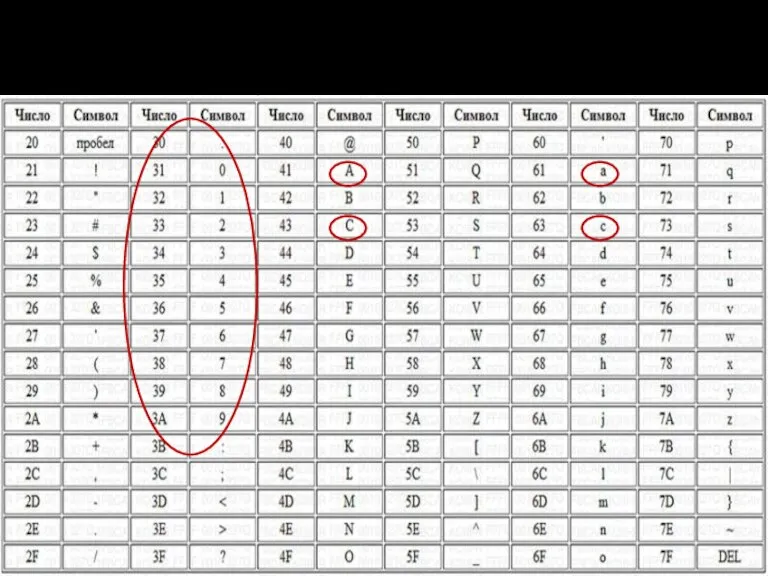
- 94. До недавнего времени наиболее широко использовался код ASCII (American Standard Code for Interchange Information) – американский
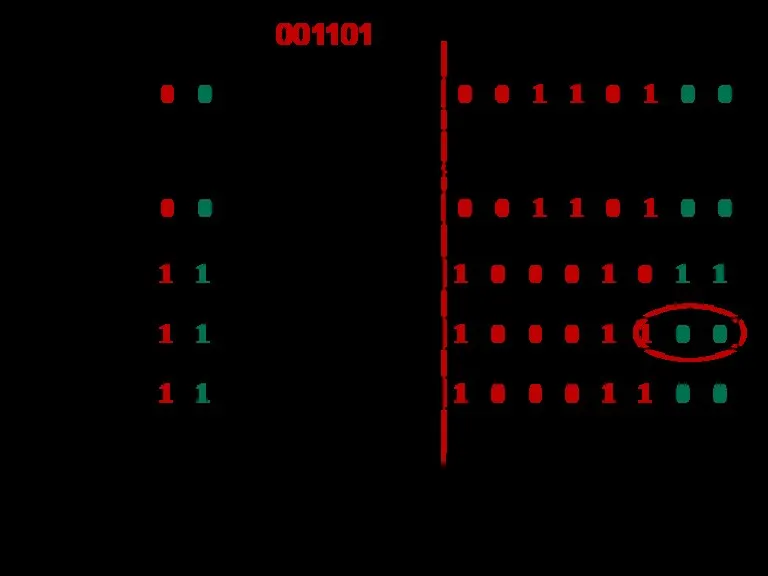
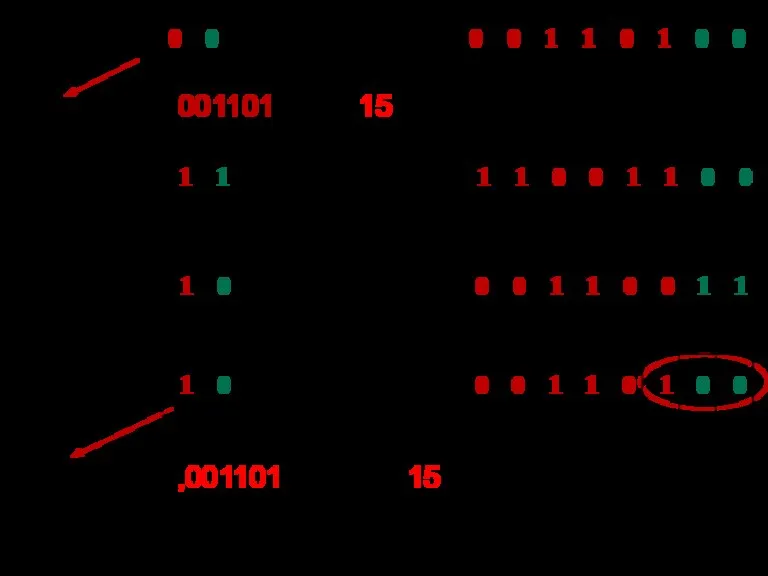
- 95. Фрагмент таблицы 8-битного кода ASCII American Standard Code for Information Interchange. Коды символов даны в 16-ричной
- 96. Пример кодировки слов way и WAY: 57(W) 41(A) 59(Y) 77(w) 61(a) 79(y)
- 97. На основе этого кода, с целью совместимости, был создан отечественный код "КОИ-8" (код обмена информацией -
- 98. Недостатком ASCII явилось ограниченное количество символов (256), что затрудняло его использование для представления многоязычных текстов. Для
- 99. Эта система позволяет закодировать свыше миллиона символов (1 114 112 ). Большинство символов, используемых в основных
- 100. Стандарт UNICODE имеет три формы: 32-битную (UTF-32); 16-битную (UTF-16); 8-битную (UTF-8). Весьма распространенная восьмибитная форма UTF-8
- 101. Спасибо за внимание !!
- 102. Лабораторная работа "Форматы представления чисел в цифровых процессорах"
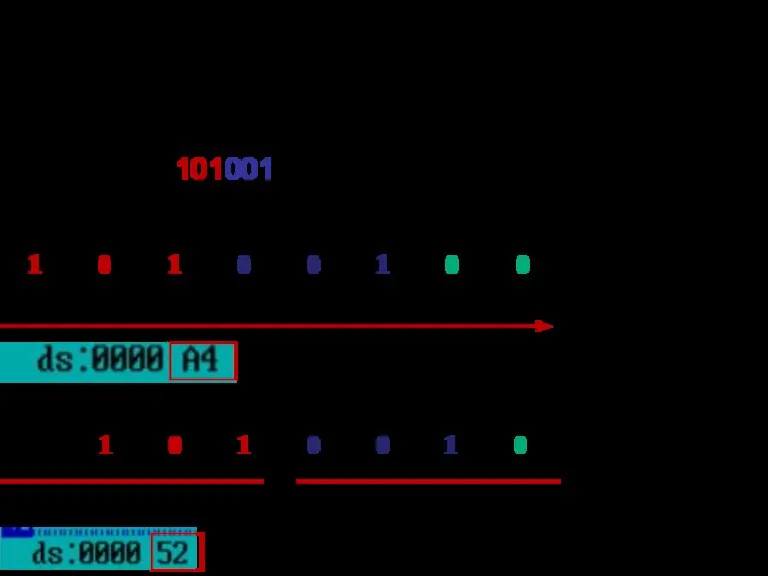
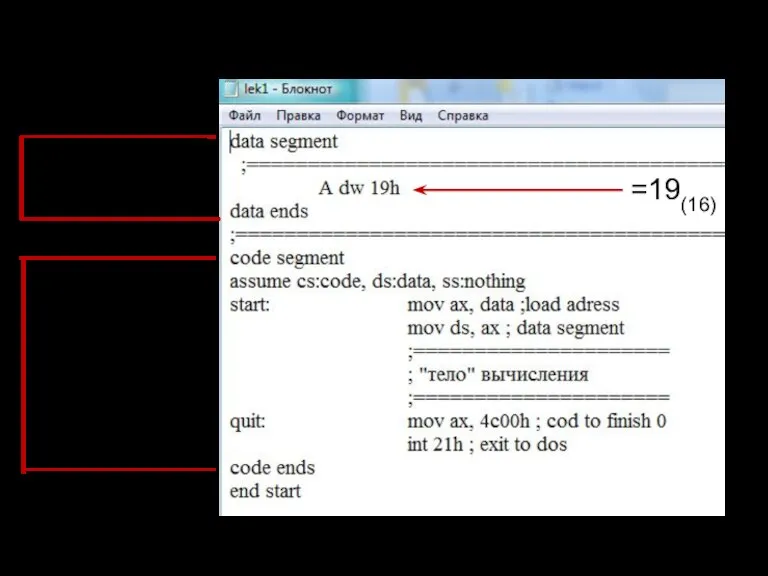
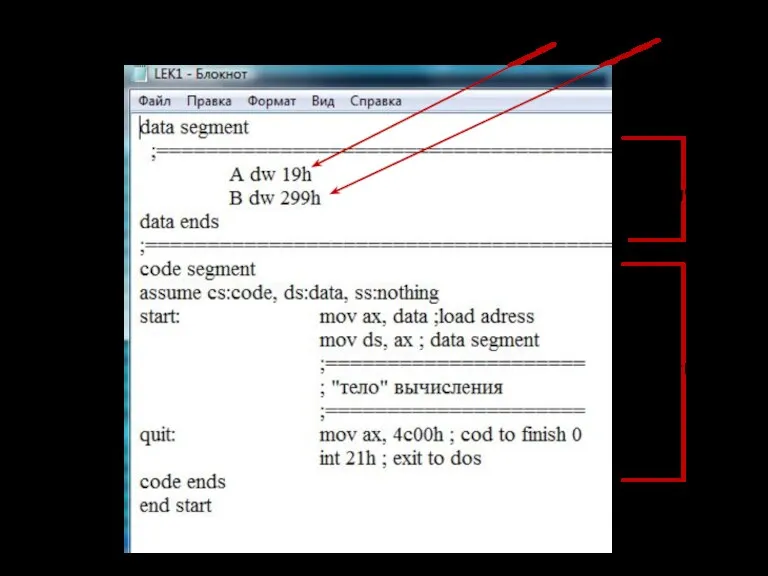
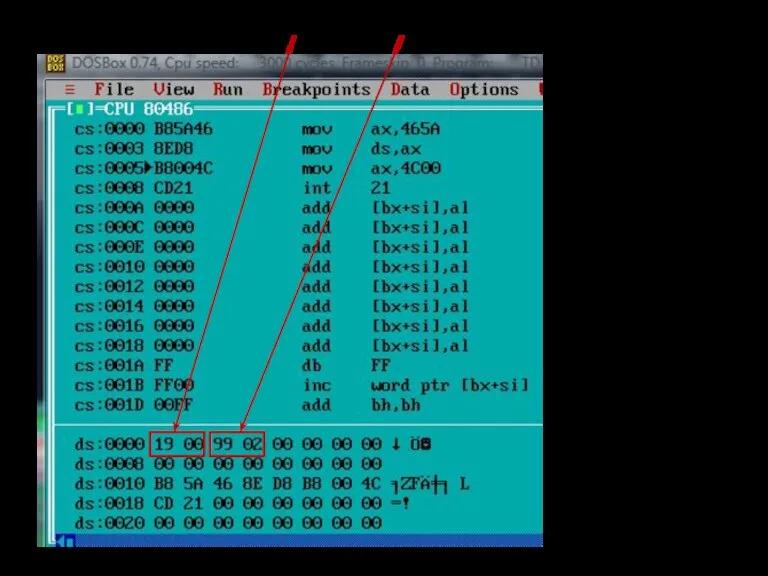
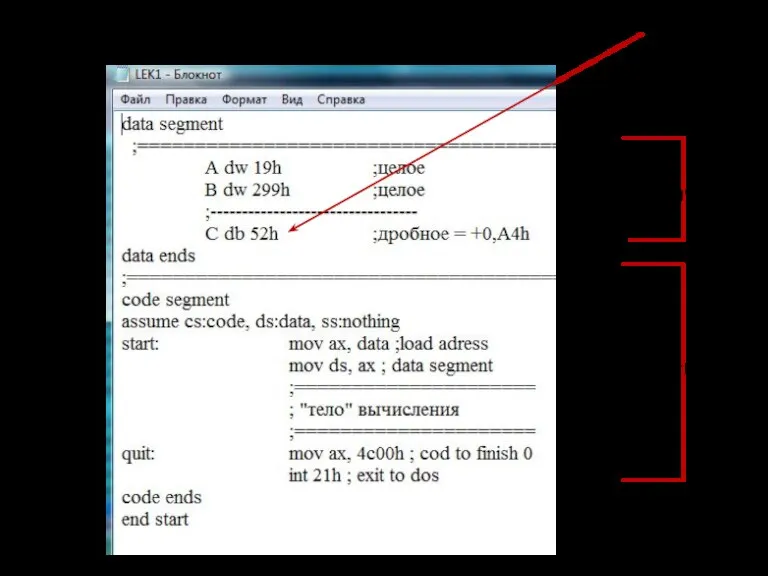
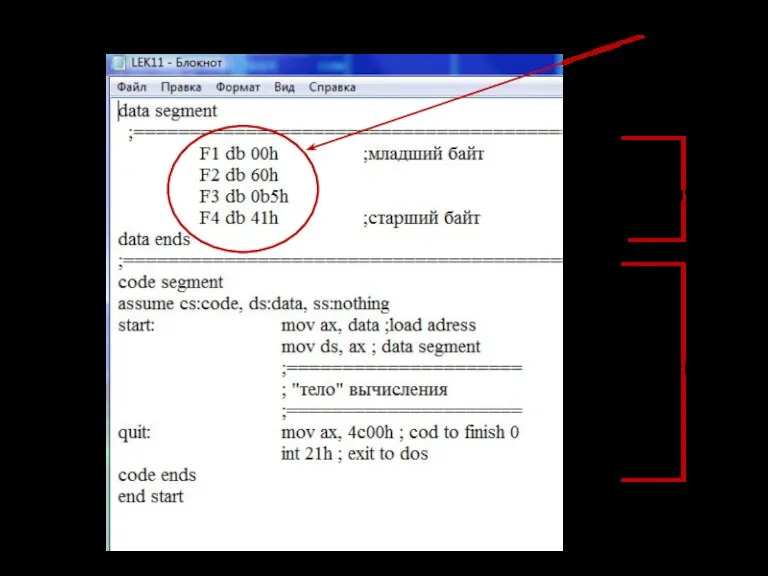
- 103. Целые числа (на ассемблере для 16-разрядного процессора) сегмент данных сегмент кода =19(16)
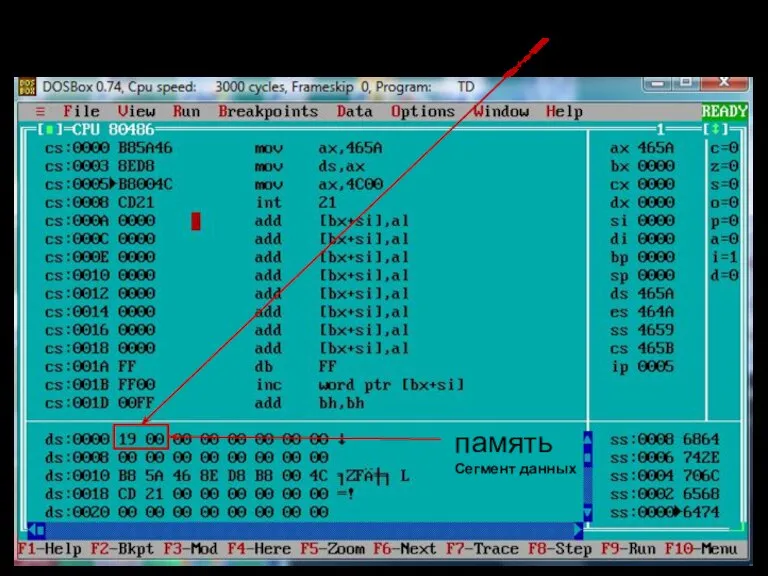
- 104. Целые числа ds – сегмент данных; cs – сегмент кода =19(16) память Сегмент данных
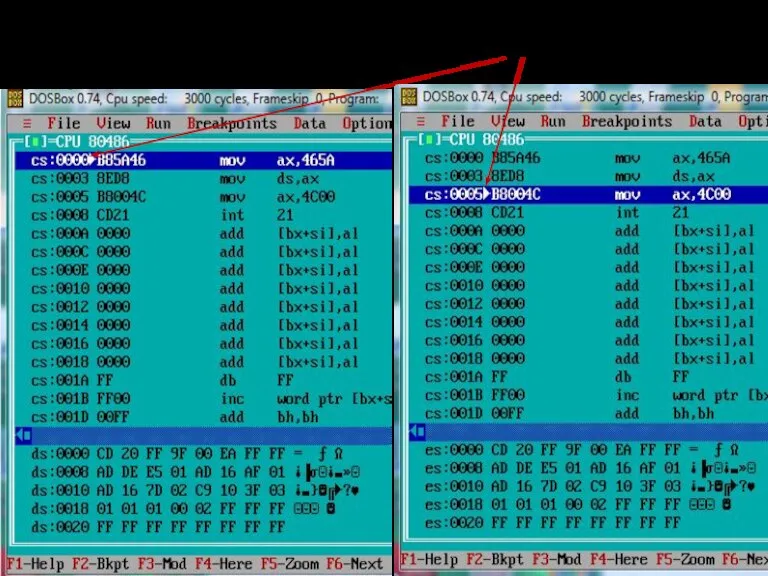
- 105. Чтобы отобразить сегмент данных нужно по клавише F8 выполнить первые две команды программы:
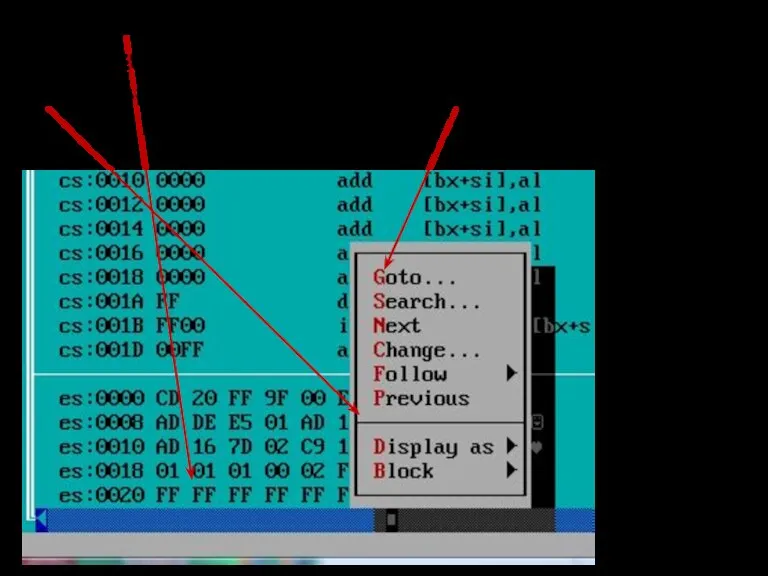
- 106. Переключиться на сегмент данных (щелкнуть на нем правой кнопкой) и левой кнопкой, вызвать контекстное меню. Выбрать
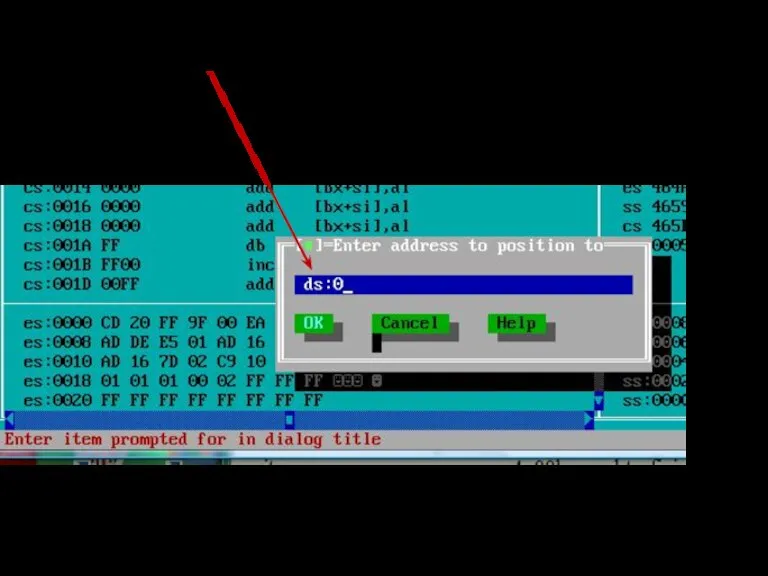
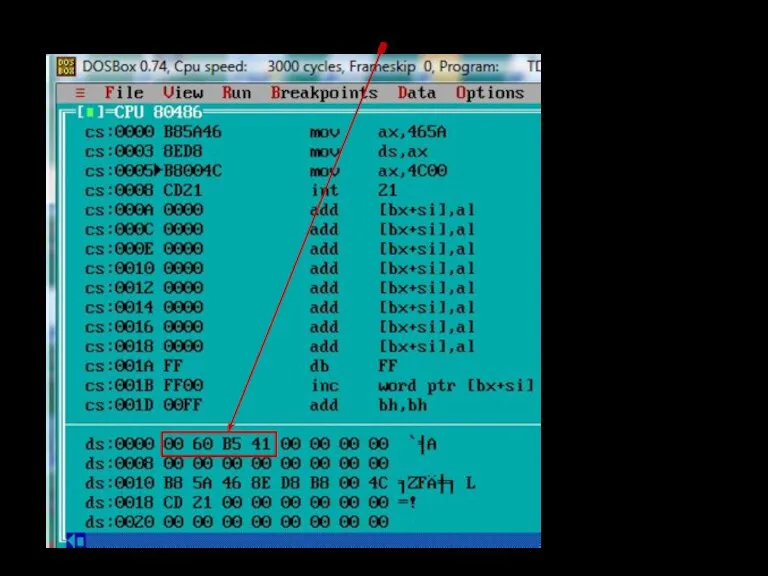
- 107. Задать отображение памяти начиная с адреса 0000 в сегменте данных, нажать Enter:
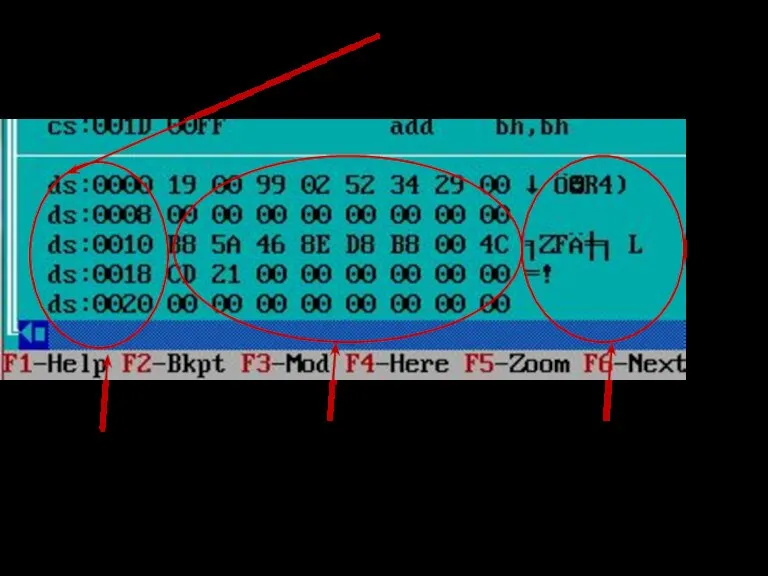
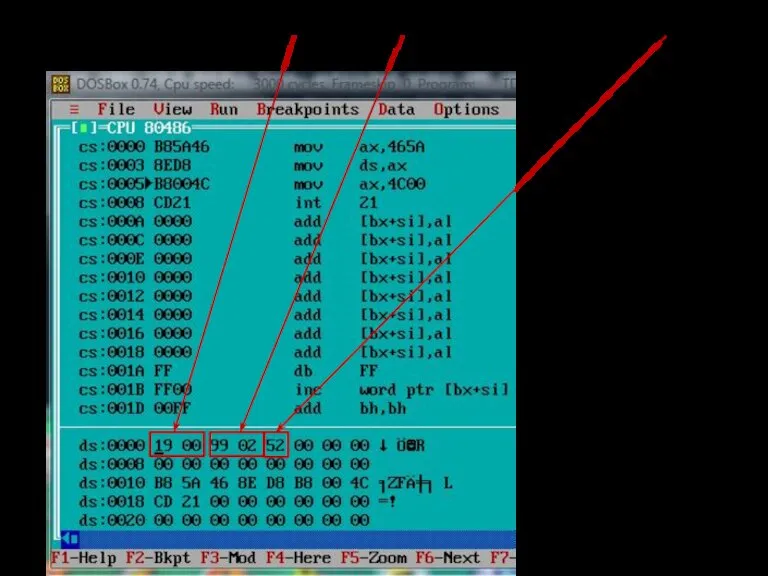
- 108. Побайтовое отображение памяти с ds:0 адреса памяти содержимое по адресам памяти символьный код байтов
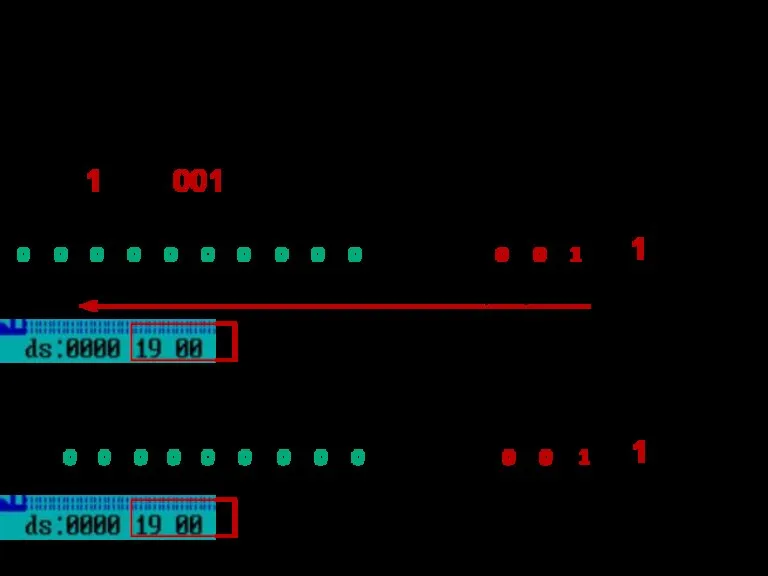
- 109. Целые числа =19(16)и 299(16) сегмент данных сегмент кода
- 110. Целые числа 19(16) и 229(16)
- 111. Формат представления правильных дробей Дробное число М1, заданное в восьмеричной системе счисления, представить в формате с
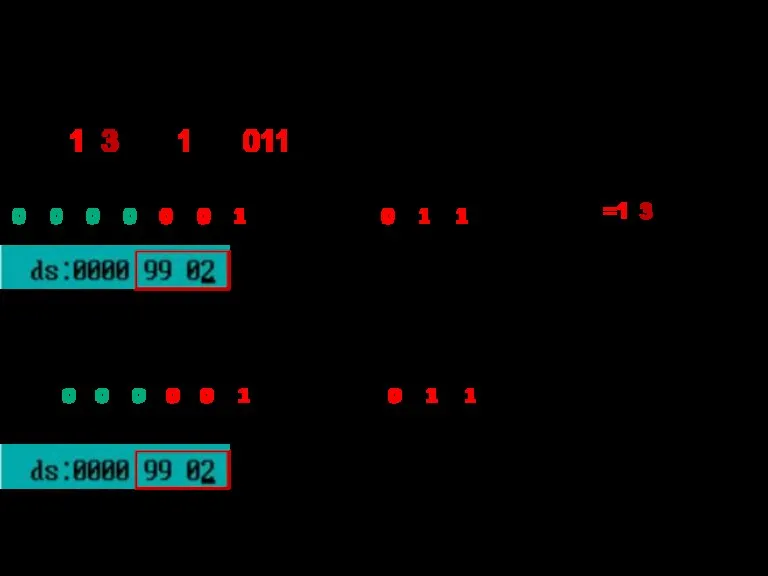
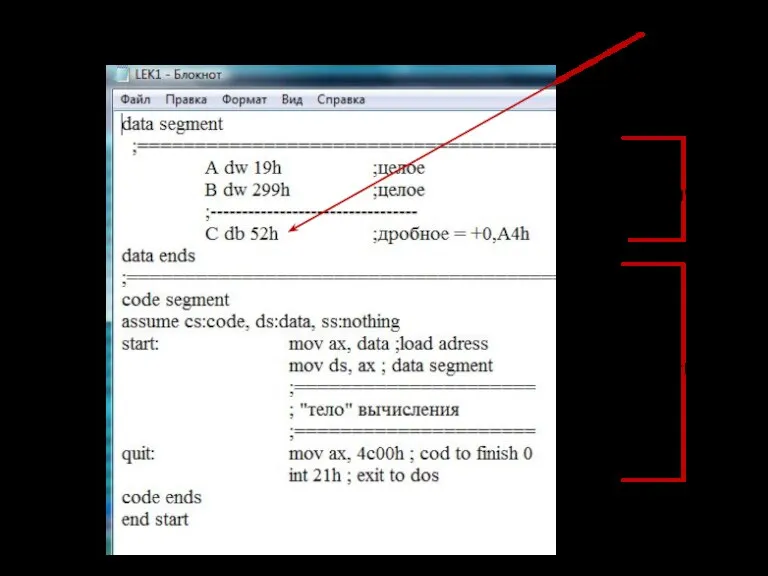
- 112. сегмент данных сегмент кода Целые числа 19(16) и 229(16) и дробное со знаком +0,A4(16)
- 113. Целые числа 19(16) и 229(16) и дробное 0,A4(16)
- 114. сегмент данных сегмент кода Целые числа 19(16) и 229(16) и дробное со знаком +0,A4(16)
- 115. Целые числа 19(16) и 229(16) и дробное 0,A4(16)
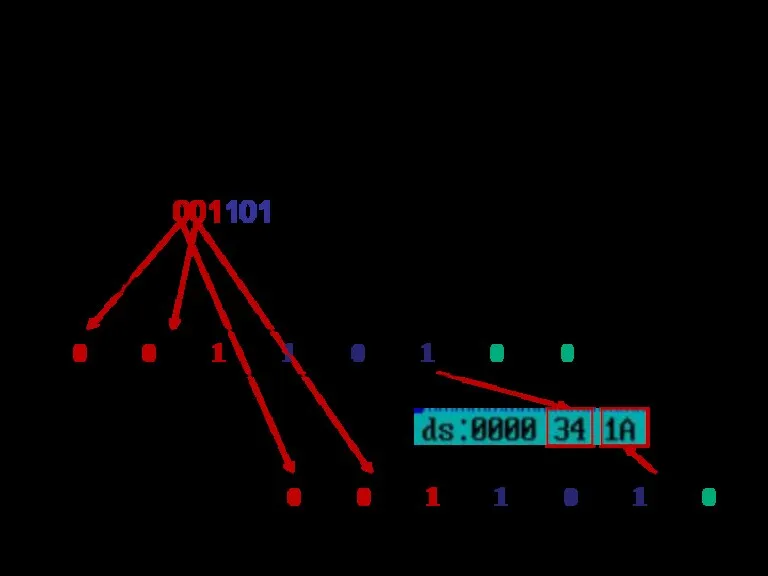
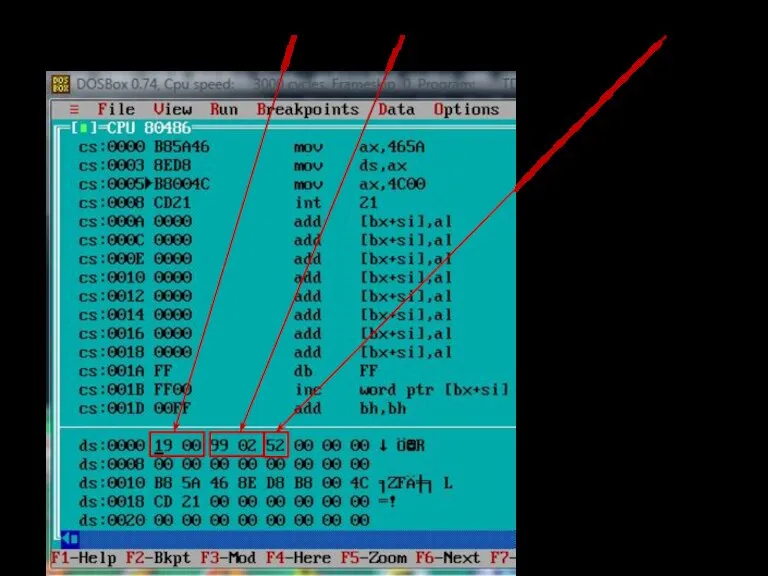
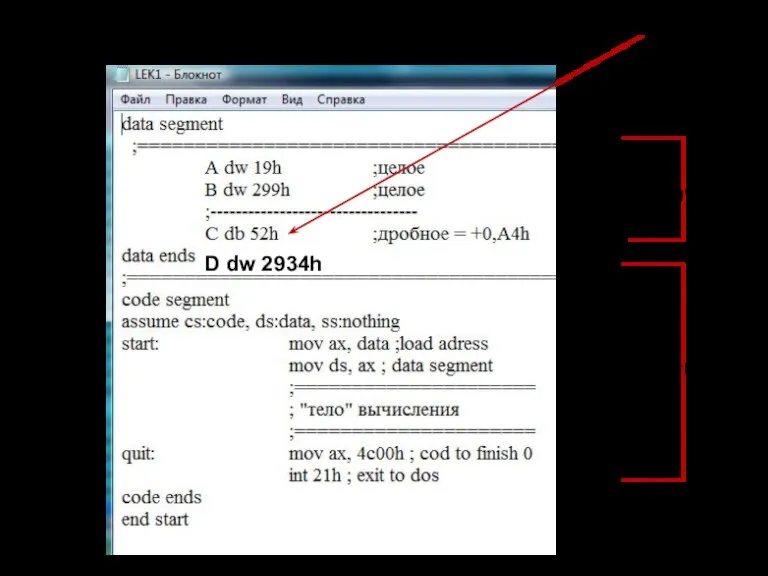
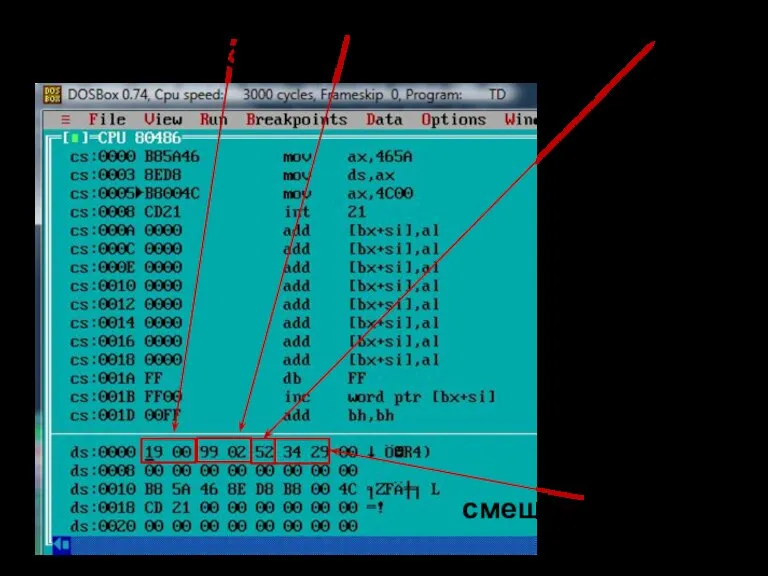
- 116. сегмент данных сегмент кода D dw 2934h
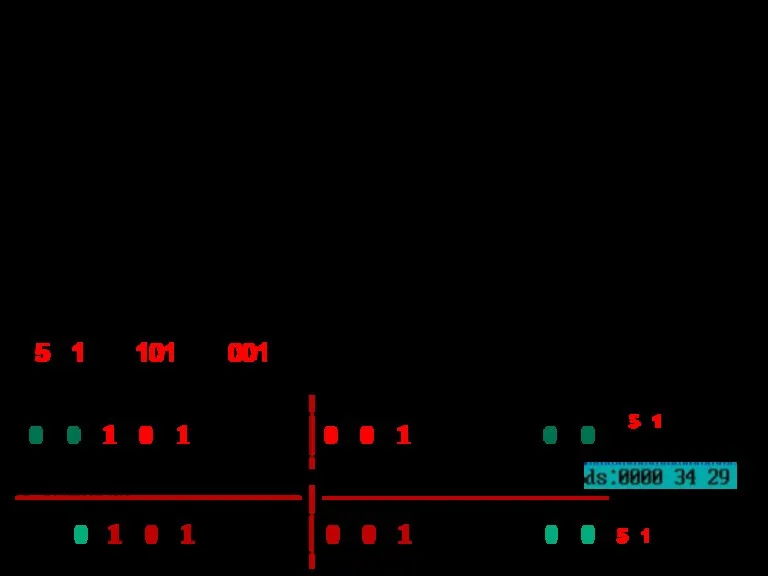
- 117. смешанное 29,34(16) Целые числа 19(16) и 229(16); дробное 0,A4(16); смешанное 29,34(16)
- 118. Вещественное число 16,АС(16) в формате КВ сегмент данных сегмент кода
- 119. Вещественное число 16,АС(16) в формате КВ
- 121. Скачать презентацию








































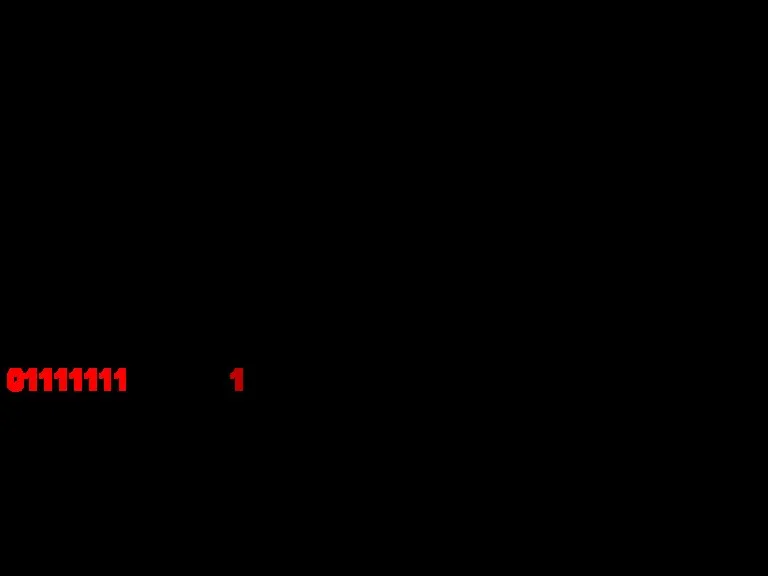
























 Сборка ПК
Сборка ПК Профессиональные дефициты сотрудников НКО как барьеры информационной открытости
Профессиональные дефициты сотрудников НКО как барьеры информационной открытости Работа по системе компьютерной графики
Работа по системе компьютерной графики Сопровождение инженерных проектов
Сопровождение инженерных проектов Тестовое задание для Frontend разработчика
Тестовое задание для Frontend разработчика Основы методологии
Основы методологии Тест по основам программирования. Pascal
Тест по основам программирования. Pascal Проект Dengerouscraft,1.1.X
Проект Dengerouscraft,1.1.X Программирование и основы алгоритмизации. Тема 6. Объектно-ориентированное программирование. Перегрузка и шаблоны
Программирование и основы алгоритмизации. Тема 6. Объектно-ориентированное программирование. Перегрузка и шаблоны Создание игры с искусственным интеллектом на UE4
Создание игры с искусственным интеллектом на UE4 Переменные. Присваиваем значения
Переменные. Присваиваем значения Анализ электронных таблиц и диаграмм
Анализ электронных таблиц и диаграмм Информационные технологии (ИТ): Основные понятия, эволюция. Тема 1
Информационные технологии (ИТ): Основные понятия, эволюция. Тема 1 Понятие об информационных системах и автоматизации информационных процессов
Понятие об информационных системах и автоматизации информационных процессов Ардуино
Ардуино Создание молекулярных ассемблеров
Создание молекулярных ассемблеров № 5 память.управление памятью
№ 5 память.управление памятью Программное обеспечение персонального компьютера
Программное обеспечение персонального компьютера Основные примитивы AutoCad при создании графических объектов
Основные примитивы AutoCad при создании графических объектов SOAP - протокол обмена структурированными сообщениями
SOAP - протокол обмена структурированными сообщениями Rozproszone systemy komputerowe
Rozproszone systemy komputerowe Экономика и финансы. Творческая школа Хорошие презентации
Экономика и финансы. Творческая школа Хорошие презентации Телеканал НТВ
Телеканал НТВ Текст как информационный объект. 11 класс
Текст как информационный объект. 11 класс Формы представления информации
Формы представления информации Кодирование цветовой информации
Кодирование цветовой информации VAlve. Игра
VAlve. Игра Java для начинающих
Java для начинающих