Содержание
- 2. Основы логики Логические операции
- 3. Философ Платон (428—347). Сочинения Платона содержат важный вклад в развитие философской логики. Платон ставит три вопроса:
- 4. Логика Аристотеля, в частности его теория силлогизма, имела огромное влияние на западную мысль. Его труды по
- 5. Немецкий ученый Готфрид Лейбниц (1646 - 1716) заложил основы математической логики. Он пытался построить первые логические
- 6. «Логика» ( от др.гр. logos) - слово, мысль, понятие, рассуждение, закон Формальная логика – наука о
- 7. Высказывание – это повествовательное предложение, о котором всегда можно сказать, истинно оно или ложно. Примеры высказываний:
- 8. Задание№1 Являются ли эти предложения высказываниями? Вы были в театре? Завтра я не пойду на каток.
- 9. Логическая переменная – высказывание в булевой алгебре, которое может принимать лишь два значения 1(истина) и 0
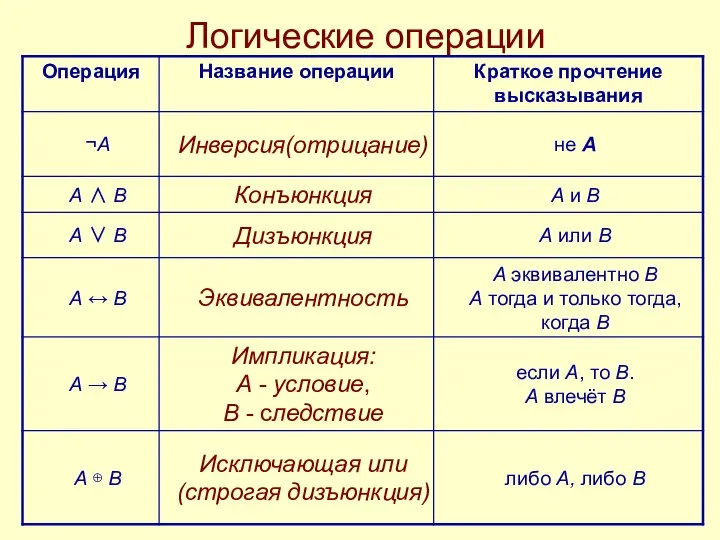
- 10. Логические операции
- 11. Логическая операция ИНВЕРСИЯ (отрицание): соответствует словам неверно, что... и частице не; обозначение —, ¬; Инверсия логической
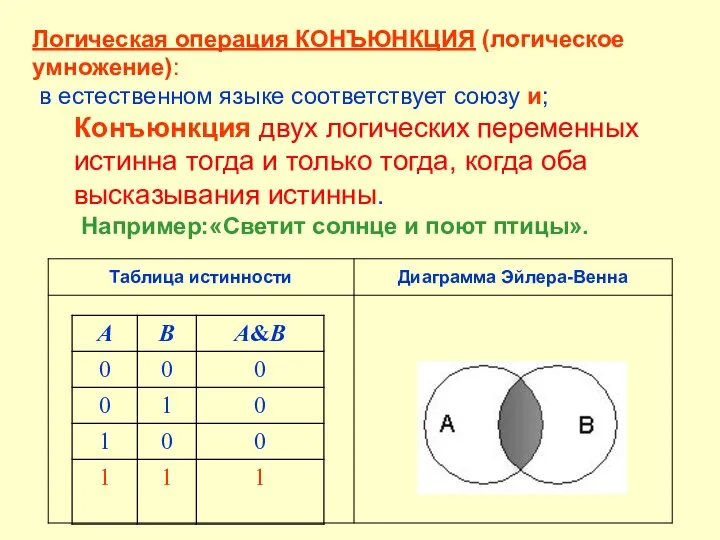
- 12. Логическая операция КОНЪЮНКЦИЯ (логическое умножение): в естественном языке соответствует союзу и; Конъюнкция двух логических переменных истинна
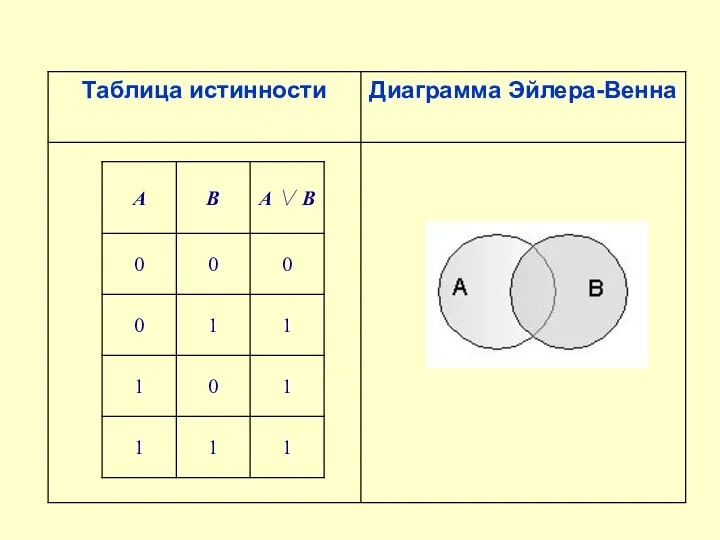
- 13. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение): соответствует союзу или; обозначение +; V; Дизъюнкция двух логических переменных ложна
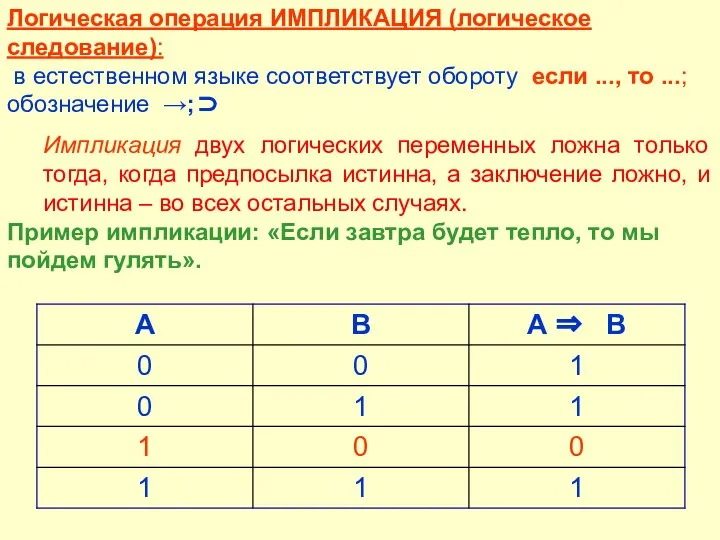
- 15. Логическая операция ИМПЛИКАЦИЯ (логическое следование): в естественном языке соответствует обороту если ..., то ...; обозначение →;⊃
- 16. Логическая операция ЭКВИВАЛЕНТНОСТЬ (равнозначность): в естественном языке соответствует оборотам речи тогда и только тогда; в том
- 17. Логическая операция Исключающая или (Строгая дизъюнкция) в естественном языке соответствует оборотам речи либо… , либо.. обозначение
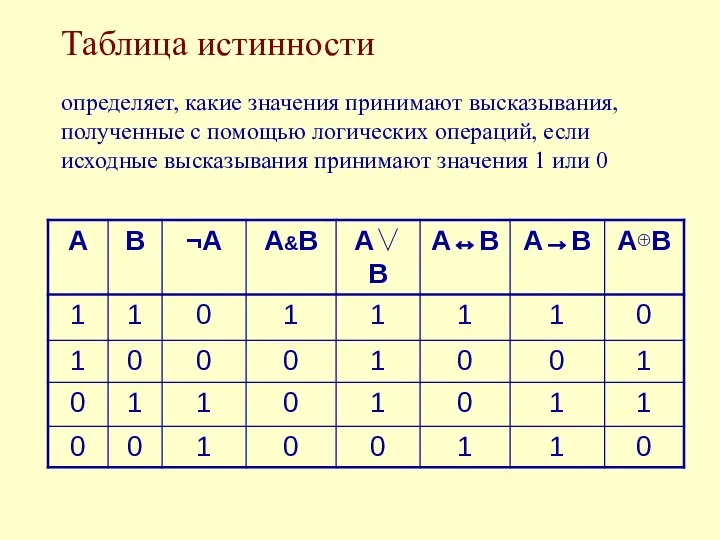
- 18. Таблица истинности определяет, какие значения принимают высказывания, полученные с помощью логических операций, если исходные высказывания принимают
- 20. Скачать презентацию












 Библиотека Кировских островов
Библиотека Кировских островов Итераторы и функциональные объекты
Итераторы и функциональные объекты Основы программирования (на языке Си). Массивы
Основы программирования (на языке Си). Массивы Проект Витрина
Проект Витрина Шаблоны писем
Шаблоны писем Профессия гейм-дизайнер
Профессия гейм-дизайнер Урок - игра Основы информатики
Урок - игра Основы информатики Мировой класс лидирующих компаний в цифровой струйной печати
Мировой класс лидирующих компаний в цифровой струйной печати Архитектура современной ЭВМ. Состав и характеристики комплектующих современного персонального компьютера
Архитектура современной ЭВМ. Состав и характеристики комплектующих современного персонального компьютера Skype-конференция
Skype-конференция 3. Выбор жизненного цикла ИТ-проекта.Использование гибких подходов в управлении ИТ-проектами
3. Выбор жизненного цикла ИТ-проекта.Использование гибких подходов в управлении ИТ-проектами Примеры использования внешних устройств. Программное обеспечение внешних устройств
Примеры использования внешних устройств. Программное обеспечение внешних устройств Создание комплексной системы обеспечения информационной безопасности инфраструктуры Росреестра
Создание комплексной системы обеспечения информационной безопасности инфраструктуры Росреестра Хранители Равновесия
Хранители Равновесия База данных
База данных Технические новинки первой мировой войны
Технические новинки первой мировой войны Структуры данных: стеки, деки, очереди
Структуры данных: стеки, деки, очереди Интерактивная доска (ИД)
Интерактивная доска (ИД) Презентация на тему Примеры моделирования
Презентация на тему Примеры моделирования  Информационные технологии. Тема № 3. Основы защиты информации
Информационные технологии. Тема № 3. Основы защиты информации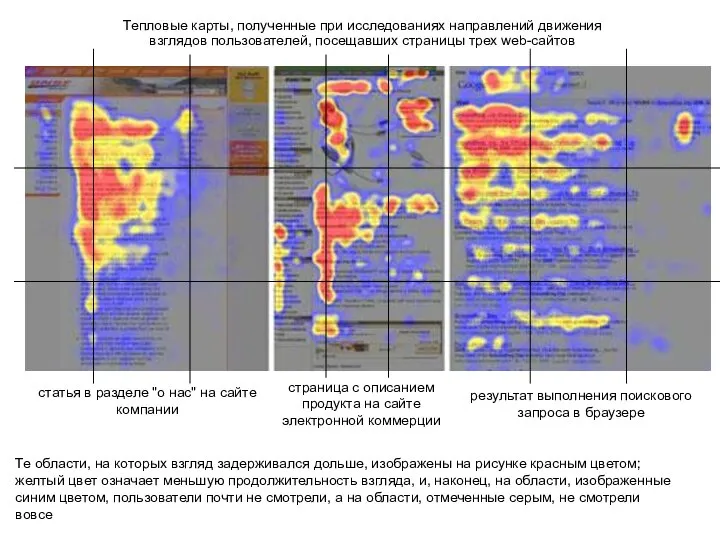 Тепловые карты, полученные при исследованиях направлений движения взглядов пользователей, посещавших страницы трех web-сайтов
Тепловые карты, полученные при исследованиях направлений движения взглядов пользователей, посещавших страницы трех web-сайтов Функциональное программное обеспечение решения управленческих задач
Функциональное программное обеспечение решения управленческих задач Дизайн и графика. Web-страницы
Дизайн и графика. Web-страницы Источники пространственных данных. Их типы. Способы получения данных
Источники пространственных данных. Их типы. Способы получения данных Организация сетевого администрирования
Организация сетевого администрирования 3
3 One Drive
One Drive Создание групп (сообществ) в образовательной сети
Создание групп (сообществ) в образовательной сети