ИиОИТ 2019. Лекция 2. Информация и ее свойства_2020 (1)

В основе информации лежат данные.
Данные – это зарегистрированные сообщения или сигналы, которые по каким-либо причинам не используются, а только хранятся. В том случае, когда появляется возможность использовать эти данные для уменьшения неопределенности знаний о чем-либо, данные превращаются в информацию.

Пример.
Номера телефонов, записанные на листе – это просто набор чисел, данные. Если снабдить эти данные фамилией абонента, то эти данные превращаются в информацию, т.к. они показывают владельцев телефонов.

Источниками информации являются объекты или явления, порождающие различные сигналы.
Потребителями информации являются различные процессы или объекты.
Пути и процессы, обеспечивающие передачу информации от источника к потребителю, называются информационными коммуникациями.

Действия с информацией
Действия с информацией выполняются путем операций над данными, которые являются носителем информации.
Основные операции над данными:
1. Создание 2. Хранение
3. Обработка 4. Поиск
5. Копирование 6. Передача 7. Прием 8.Разрушение
Разработка технологий выполнения этих операций – одна из важнейших задач информатики.

Классификация информации.

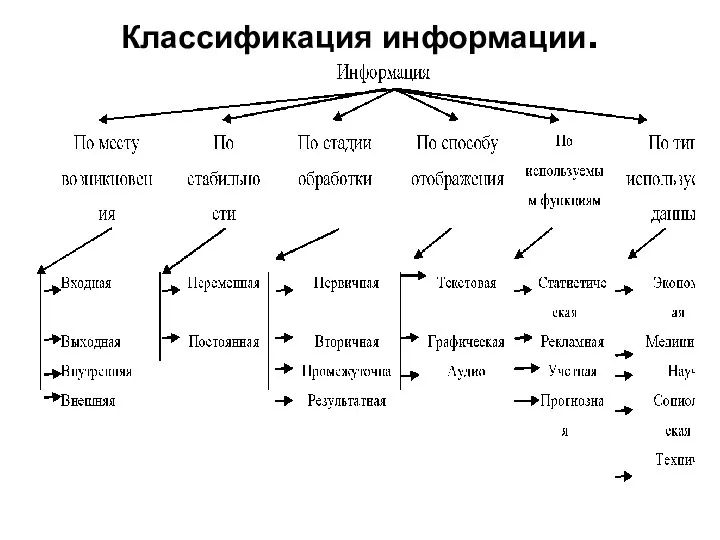
Входная информация – это информация, которую потребитель информации получает для обработки.
Выходная информация – это информация, которую потребитель информации выдает во внешнюю среду после обработки. Выходная информация одного потребителя может служить входной для других потребителей.
Внутренняя информация возникает внутри потребителя, внешняя – за его пределами.

Переменная информация – это информация, которая меняется с определенной периодичностью.
Постоянная информация – это информация, остающаяся неизменной некоторый достаточно длительный период времени
Первичная информация – это информация, которая существует перед началом обработки.
Вторичная информация является результатом обработки первичной информации.
Промежуточная информация – это вторичная информация, которая используется для дальнейших расчетов.
Результатная информация – это вторичная информация, которая в дальнейших расчетах не используется.

Текстовая информация – совокупность алфавитных, цифровых и специальных знаков, с помощью которых информация представляется на носителях информации (например, бумаге).
Графическая информация – это различного рода графики, схемы, рисунки и т.п.
Звуковая информация – это набор звуков, воспринимаемых человеком или техническим устройством.

Классификация по используемым функциям зависит от применения информации в конкретных областях. В социологии и менеджменте, например, широко используется социологическая информация, рекламная, прогнозная и др.
По типу используемых данных информация делится в зависимости от конкретной области, в которой данные возникают и используются. Например, социологическая информация – это совокупность сведений, отражающих социальные процессы и служащих для управления этими процессами и коллективами людей в социальной сфере.
Возможны и другие способы классификации. Например, по способу обработки техническими устройствами информацию можно разделить на цифровую и аналоговую. Цифровая информация обрабатывается как дискретная последовательность сигналов, а аналоговая – как непрерывный сигнал.

Свойства информации.
Объективность информации означает отсутствие субъективных факторов в процессе получения и обработки информации. Данное свойство характеризует независимость информации от чьего-либо мнения или сознания. Объективную информацию можно получить с помощью каких-либо измерений (например, точными приборами).
Например, информация о том, что автомобиль ехал быстро, не всегда объективна. Информация о том, что автомобиль ехал со скоростью 150 км/ч объективна, если она получена с помощью исправной камеры фиксации скоростного режима.

Полнота информации определяет достаточность данных для принятия решений или создания новых данных на основе уже имеющихся. О полноте информации можно говорить, когда какая-либо дополнительная информация об объекте будет уже избыточна.
Неполная информация может привести к ошибочным выводам и действиям. Например, сообщение «Температура на улице 10 градусов» без уточнения «тепла» или «мороза» может привести к неправильному выбору человеком верхней одежды.

Достоверность информации характеризует то, как информация отражает истинное положение дел, степень доверия, с которой потребитель информации ее воспринимает. Достоверность информации носит статистический характер и оценивается в определенной шкале. Недостоверная информация может привести к неправильным решениям. Например, недостоверная информация в рекламе может привести к ошибкам при покупке товара.
Достоверная информация со временем может стать недостоверной, так как она может устаревать и не отражать истинное положение дел. Достоверность информации зависит от достоверности источника информации (полностью надёжный, чаще всего надёжный, довольно надёжный и так далее до совершенно ненадёжного и того, чей статус не определён).

Точность информации определяет степень близости получаемой информации к реальному состоянию объекта, процесса, явления. Например, десятичное число может быть записано с точностью до трех десятичных знаков. В этом случае можно оценить максимально возможную ошибку при использовании этого числа (чем отличается от достоверности? Может ли информация быть достоверной, но неточной?)

Адекватность информации – это определенный уровень соответствия создаваемого с помощью полученной информации образа реальному объекту (чем отличается от достоверности?, может ли быть информация достоверной, но не адекватной?; чем отличается от объективности?).
Доступность информации – мера возможности получить ту или иную информацию в приемлемое время в необходимом виде. Например, секретные документы, хранящиеся в архиве, невозможно получить людям, которым доступ к таким архивам запрещен. В этом случае информация является недоступной.

Актуальность (своевременность) информации – это степень соответствия информации текущему моменту времени, вовремя полученная информация. Например, телеграмма о приезде друзей, полученная своевременно, позволит вовремя их встретить.

Измерение информации.
Объем данных Vд информации. Измеряется в количестве символов, входящих в данные.
Объем данных в ВТ измеряется в битах. Бит – это один символ алфавита, состоящего из двух символов – 0 или 1.
Восемь битов образуют 1б (один байт) . Таким образом, байт – это символ алфавита из 256 символов (почему?).
Более крупные единицы измерения объемов данных:
1 Кб (килобайт)=1024 б=210 байт,
1Мб (Мегабайт)=1024 Кб=220 байт,
1Гб (гигабайт)=1024 Мб =230 байт,
1Тб (терабайт)=1024 Гб=240 байт,
1Пб (петабайт)=1024 Тб=250 байт.

Количество информации.
Количество информации характеризует степень снижения неопределенности знаний об объекте или событии.
Неопределенность знаний характеризуется количеством возможных состояния объекта (возможных результатов некоторого события, например, бросания монеты или кубика)

H(α) – исходная неопределенность знаний об объекте (событии) α .
Hβ(α) – неопределенность знаний об объекте (событии) после прихода сообщения β
Iβ(α) - количество информации, которое содержится в сообщении β
Iβ(α)=H(α)-Hβ(α)

Частные случаи
Если H(α)=Hβ(α), то Iβ(α)=0 – β является тривиальным сообщением, не несущим информации.
Если Hβ(α)=0, то Iβ(α)=H(α), т.е. количество информации в сообщении β равно исходной неопределенности состояния объекта.

Понятие вероятности события
Вероятность – это мера возможности наступления некоторого события.
Пусть система может находиться в одном из N состояний, например, пусть существует N различных возможных вариантов какого-либо действия.
Пусть m – количество состояний системы (результатов действия), которые приводят к появлению события A.
Тогда вероятность реализации события А равна
p=m/N

Пример
Пусть подбрасываются 2 игральные кости. Какова вероятность, того, что выпадет 10 очков.
Общее количество вариантов 36, при этом 10 очков дают лишь следующие сочетания результатов бросания: 4+6, 5+5, 6+4, то есть существует 3 варианта, при которых реализуется искомое событие. Тогда вероятность этого события равна p10=3/36=1/12.

Формула Хартли для равновероятных состояний системы
Пусть система может находиться в одном из N равновероятных состояний, тогда до прихода сообщения неопределенность знаний о ней равна (по Р.Хартли)
H(α) =log2N
Пусть после прихода сообщения β количество неопределенных ситуаций уменьшилось и стало равно m. Тогда неопределенность знаний о системе после прихода сообщения стала равна
Hβ(α)=log2m
Отсюда количество информации в сообщении равно
Iβ(α)=H(α)-Hβ(α) или
Iβ(α)=log2N-log2m=log2(N/m)=log2(1/p), где p=m/N – вероятность реализации одной из оставшихся неопределенных ситуаций. Количество информации измеряется в битах.

Формула Хартли (вероятностный подход к измерению количества информации)

Пример 1.
В корзине лежат 16 белых и 8 черных шаров. Какое количество информации несет сообщение о том, что из корзины достали черный шар?
Решение.
Общее количество шаров в корзине равно 24, вероятность выбора черного шара равна p=8/24=1/3.
Количество информации в сообщении о том, что из корзины достали черный шар равна
I=log2(1/p)=log23=1,58 (бит)

Пример 2.
В корзине лежат 16 белых и 8 черных шаров. Какое количество информации несет сообщение о том, что из корзины достали черный шар?
Решение
Общее количество шаров в корзине равно 24 и количество возможных состояний системы, связанной с вытаскиванием шаров, равно 24 и исходная неопределенность H(α) =log224.
После прихода сообщения количество состояний системы уменьшилось до 8, поскольку стало известно, что из корзины достали черный шар (но неизвестно – какой!). Неопределенность системы стала равной Hβ(α)=log28.
Отсюда количество информации в сообщении равно
Iβ(α)=log224-log28=log2(24/8)=log2(3)=1,58 (бит) – совпадает с примером 1.

Пример 3
В корзине лежат 16 шаров, все разного цвета. Какое количество информации несет сообщение о том, что из корзины достали черный шар?
Решение.
Поскольку выбор каждого шара равновероятен, то
I=log216=4 (бита)

Пример 4
В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего в корзине шаров?
Решение.
Пусть Кб – количество белых шаров в корзине. Тогда общее количество шаров в корзине равно 18+Kб и вероятность того, что из корзины достали белый шар, равна
P= Кб /(18+ Kб), и 1/P= (18+ Kб)/ Кб
Количество информации в сообщении о том, что из корзины достали белый шар, равно по формуле Хартли
I=log2(1/P)=log2((18+ Kб)/ Кб)
По условию I=2. Замечая, что log24=2, имеем (18+ Kб)/ Кб =4.
Отсюда Кб=6, и общее количество шаров в корзине равно 18+6=24.

Смысл формулы Хартли при вероятностном подходе к измерению количества информации
Пусть имеется N равнозначных предметов. Тогда количество информации, получаемое при равновероятном выборе одного предмета из N равнозначных, равно
I=log2N.
.

Формула К.Шеннона

Пример 5 (формула Шеннона)
В корзине лежат 16 белых и 8 черных шаров. Какое количество информации несет сообщение о том, что из корзины достали шар?
Решение.
Общее количество шаров в корзине равно 24, вероятность достать белый шар равна p1=16/24=2/3, вероятность достать черный шар равна p2=8/24=1/3. Тогда
I=-(2/3*log2(2/3)+1/3*log2(1/3))=(-2/3*(-0,585)+1/3*(-1,585))=0,918 (бит)

Алфавитный подход к измерению информации
Позволяет определить количество информации, заключенной в тексте, записанном с помощью символов некоторого алфавита.
Применяется при определении количества информации, передаваемой по каналам связи, а также для оценки объемов информации на носителях данных.
Пусть имеется алфавит, использующий m символов для написания сообщений.
Лемма.
Число различных сообщений длины n, которые могут быть составлены из символов данного алфавита, равно N=mn .
Например, количество двоичных чисел (т.е.сообщений из алфавита из двух символов – 0 и 1) длины n равно N=2n

Пусть пришло сообщение длиной n. Неопределенность системы перед приходом сообщения равна H(α)=log2(mn).
Поскольку после прихода сообщения неопределенность о системе снимается (известно, какое конкретно пришло сообщение), то Hβ(α)=0 и
Iβ(α)= H(α)=log2(mn)=nlog2(m).
Если m=2, то Iβ(α)=n, т.е. количество информации в двоичной последовательности равно длине

Пример
Пусть имеется последовательность длиной 8 бит из символов 0 и 1.
β=(11000110).
Здесь m=2, n=8, тогда Iβ(α)=8 бит
Таким образом, количество информации в двоичной последовательности совпадает с объемом данных в этой последовательности.

Смысл формулы Хартли при алфавитном подходе к измерению количества информации
Если n=1, то I=log2m.
Таким образом I=log2m - это то количество информации, которое несет в себе один символ алфавита из m символов
Очевидно, что log22=1 (бит).
Тогда 1 бит – это количество информации, которое несет в себе сообщение из 1 символа в алфавите из 2-х символов.