Содержание
- 2. Содержание 1. Основные определения 2. Автоматическая кластеризация текстов: постановка задачи виды алгоритмов кластеризации алгоритмы и примеры
- 3. Вопрос В чем основные отличия кластеризации от классификации?
- 4. Основные определения Классификация (или рубрицирование) – отнесение объекта к заранее известным классам (рубрикам) классы: с заданными
- 5. Вопрос Какие цели может преследовать кластеризация?
- 6. Цели кластеризации Понять структуру множества объектов, разбив его на группы схожих объектов Пример: в маркетинге, выделяют
- 7. Пример: «интеллектуальная» группировка результатов при информационном поиске Сейчас кластеризация часто – один из этапов анализа данных
- 8. Формальная постановка задачи автоматической кластеризации Имеется множество объектов D = {d1, …, d|D|} Существует множество «тематических
- 9. Какими должны быть кластеры? Внутри каждого кластера должны оказаться «похожие» объекты, а объекты разных кластеров должны
- 10. Кластеризация текстов (документов) Документов представляются как вектора в пространстве признаков di = (di1, …, di|Τ|), где
- 11. Примеры мер (1) Евклидово расстояние – геометрическое расстоянием в многомерном пространстве Квадрат евклидова расстояния. Применяется для
- 12. Примеры мер (2) Расстояние Чебышева полезно для «различения» объектов, отличных в одной координате Считающее расстояние –
- 13. Задание 1 1: Карл у Клары украл кораллы 2: Клара у Карла украла кларнет 3: Клара
- 14. Задание 1. Ответ 1: Карл у Клары украл кораллы 2: Клара у Карла украла кларнет 3:
- 15. Задание 2 1: Карл у Клары украл кораллы 2: Клара у Карла украла кларнет 3: Клара
- 16. Взгляд в прошлое
- 17. Задание 2. Ответ 1: Карл у Клары украл кораллы 2: Клара у Карла украла кларнет 3:
- 18. Задание 3 1. Вычислить косинусное расстояние для w1=(1,1,1,1,0,0,0,0) и w2=(1,1,1,0,1,0,0,0) w1=(1,1,1,1,0,0,0,0) и w3=(1,1,1,1,0,0,0,0) 2. Вычислить евклидово
- 19. Задание 3. Обсуждение (1) 1: Карл у Клары украл кораллы 2: Клара у Карла украла кларнет
- 20. Задание 3. Обсуждение (2) 1: Карл у Клары украл кораллы 2: Клара у Карла украла кларнет
- 21. Виды алгоритмов кластеризации Иерархические и плоские алгоритмы иерархические строят не одно разбиение выборки на непересекающиеся кластеры,
- 22. Иерархические алгоритмы Восходящие (агломеративные): построение кластеров снизу вверх Начало: один документ – один кластер Последовательно объединяем
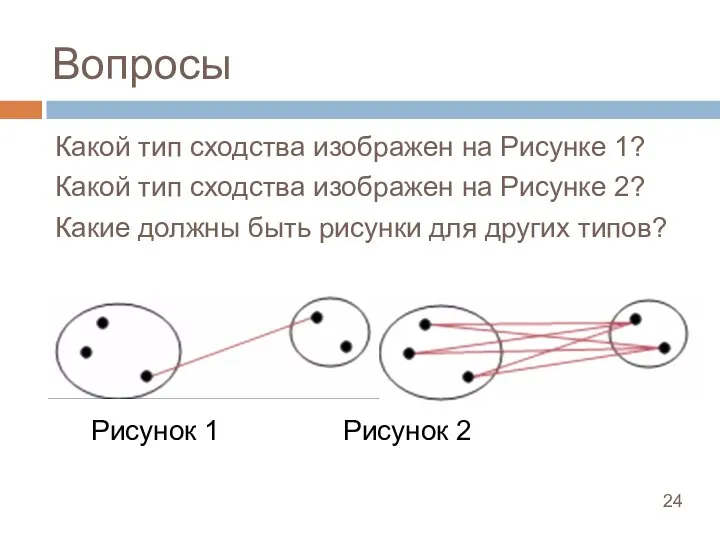
- 23. Восходящие алгоритмы: критерии объединения Сходство двух кластеров есть: сходство между их наиболее похожими документами (одиночная связь)
- 24. Вопросы Какой тип сходства изображен на Рисунке 1? Какой тип сходства изображен на Рисунке 2? Какие
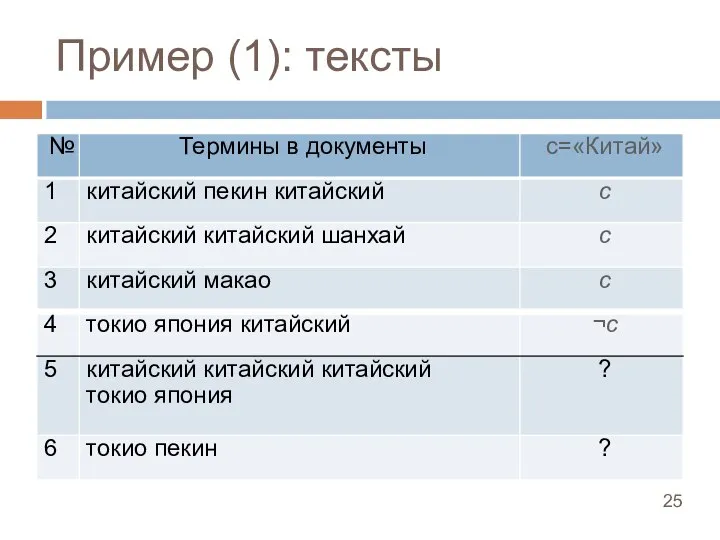
- 25. Пример (1): тексты
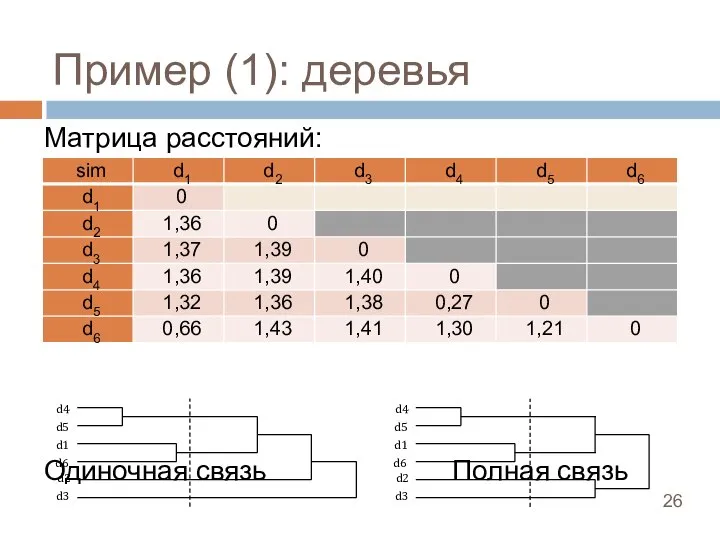
- 26. Пример (1): деревья Матрица расстояний: Одиночная связь Полная связь
- 27. Пример 2 Давайте построим дерево
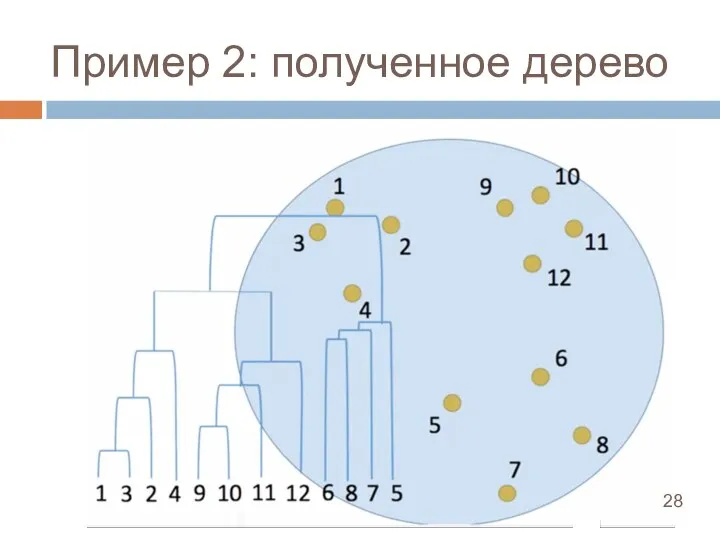
- 28. Пример 2: полученное дерево
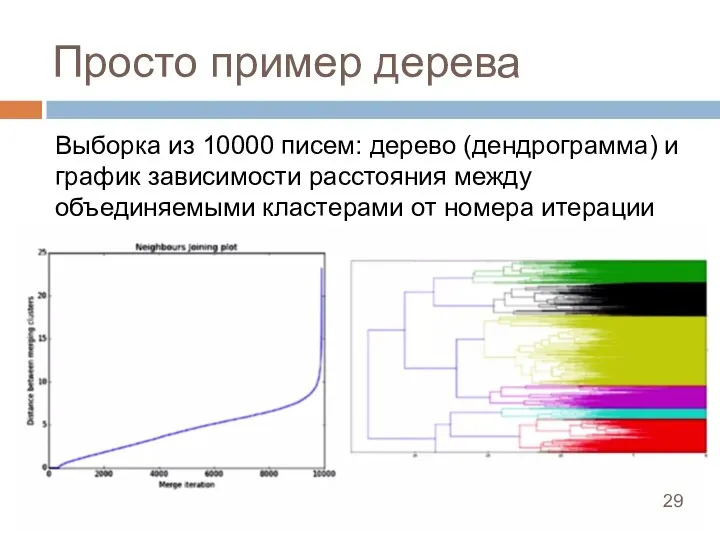
- 29. Просто пример дерева Выборка из 10000 писем: дерево (дендрограмма) и график зависимости расстояния между объединяемыми кластерами
- 30. Плоский четкий алгоритм k-средних (k-means) Входные данные: количество кластеров k множество документов как векторов di =
- 31. Оптимизируемая функция Алгоритм минимизирует среднее внутрикластерное расстояние каждая точка присваивается к тому кластеру, центр которого ближе
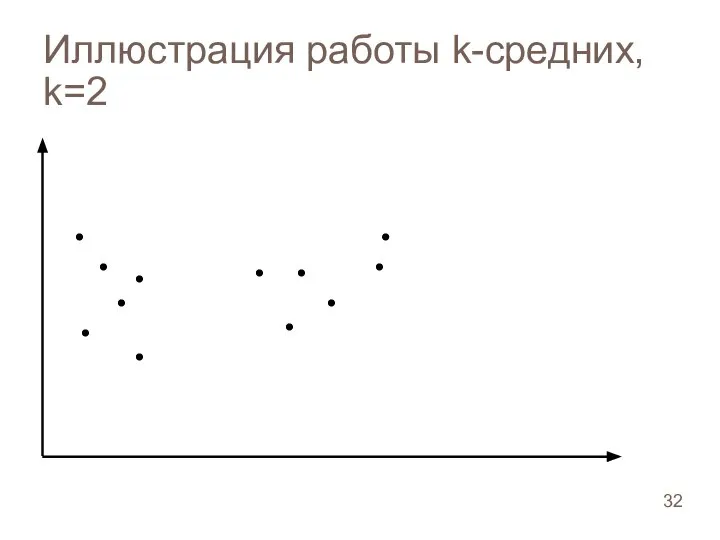
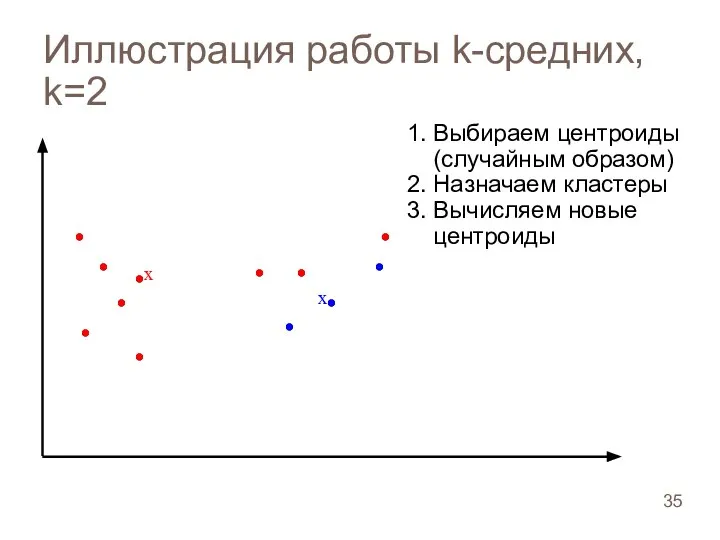
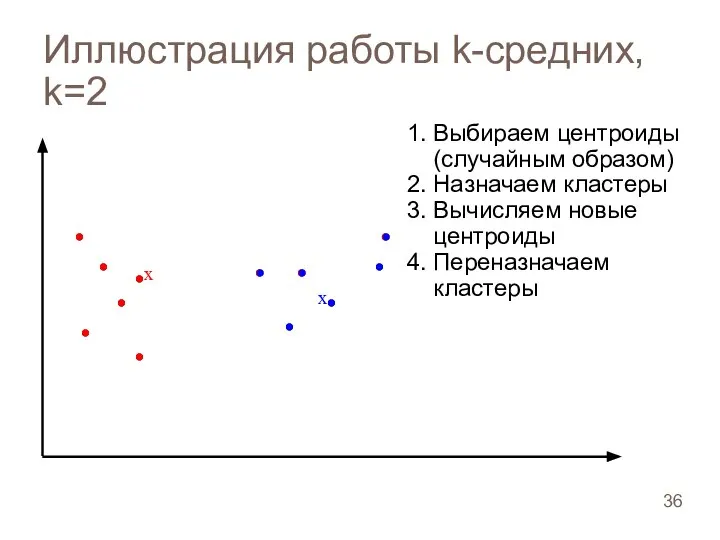
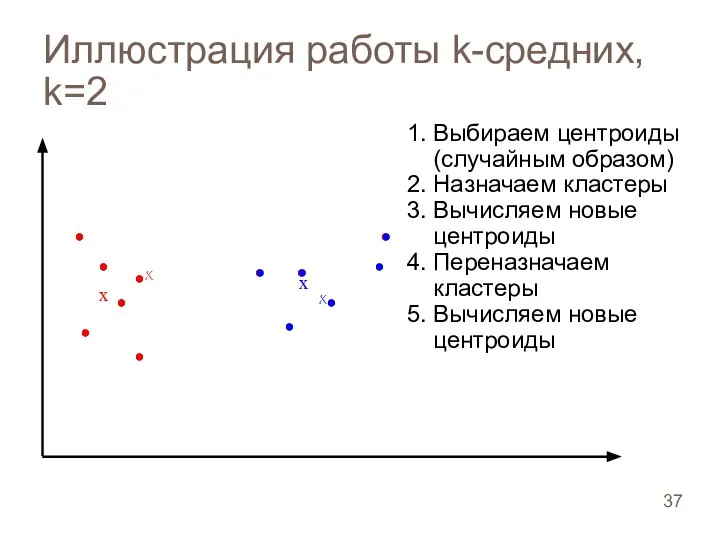
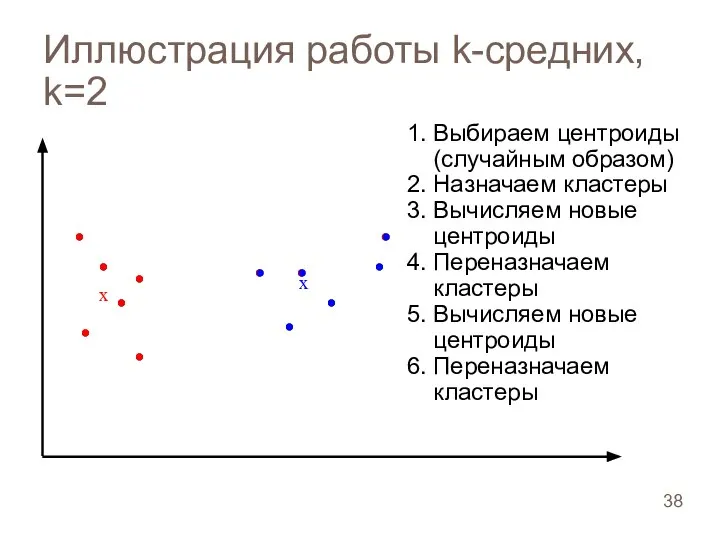
- 32. Иллюстрация работы k-средних, k=2
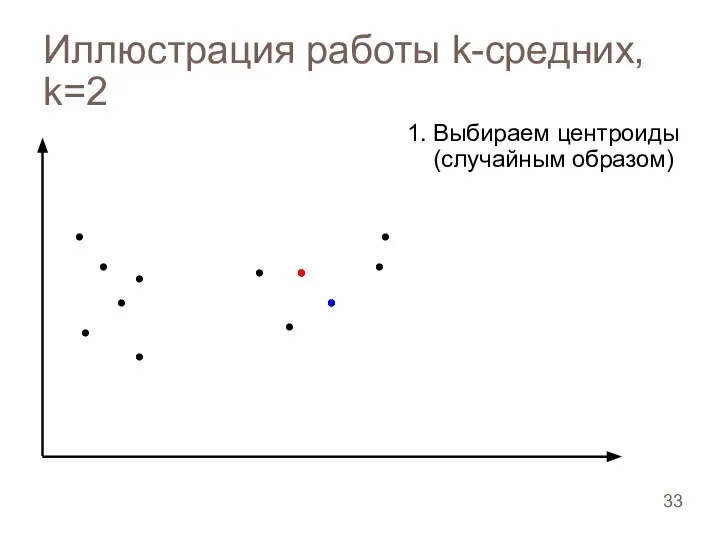
- 33. Иллюстрация работы k-средних, k=2
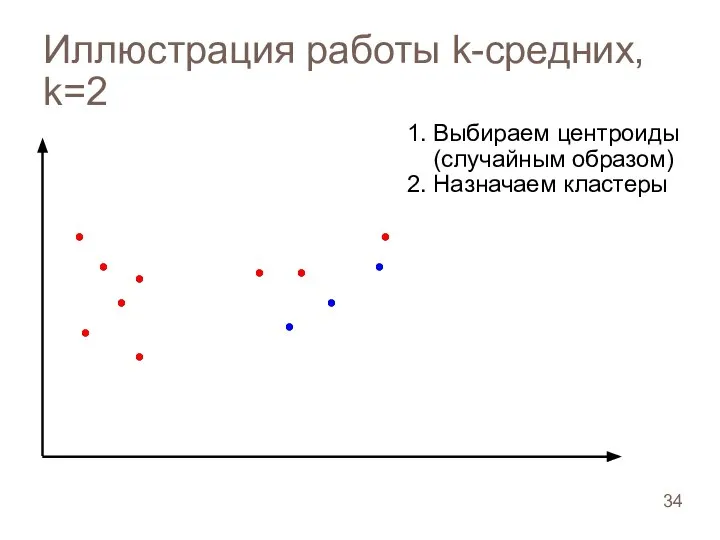
- 34. Иллюстрация работы k-средних, k=2
- 35. Иллюстрация работы k-средних, k=2
- 36. Иллюстрация работы k-средних, k=2
- 37. Иллюстрация работы k-средних, k=2
- 38. Иллюстрация работы k-средних, k=2
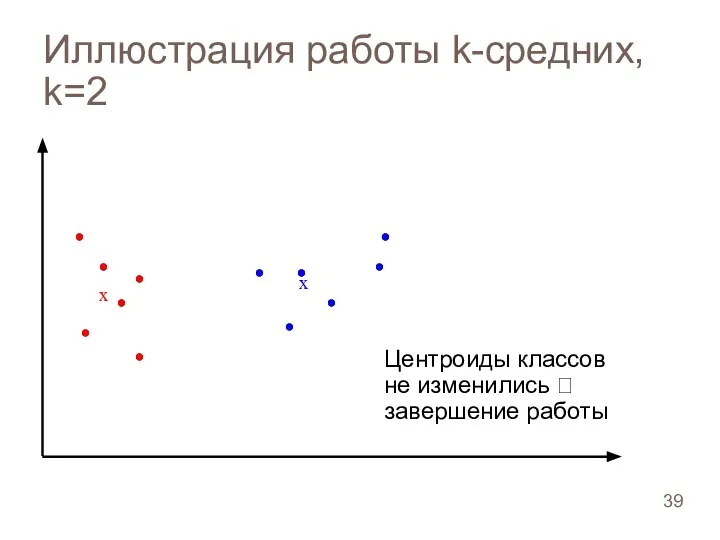
- 39. Иллюстрация работы k-средних, k=2 Центроиды классов не изменились ? завершение работы
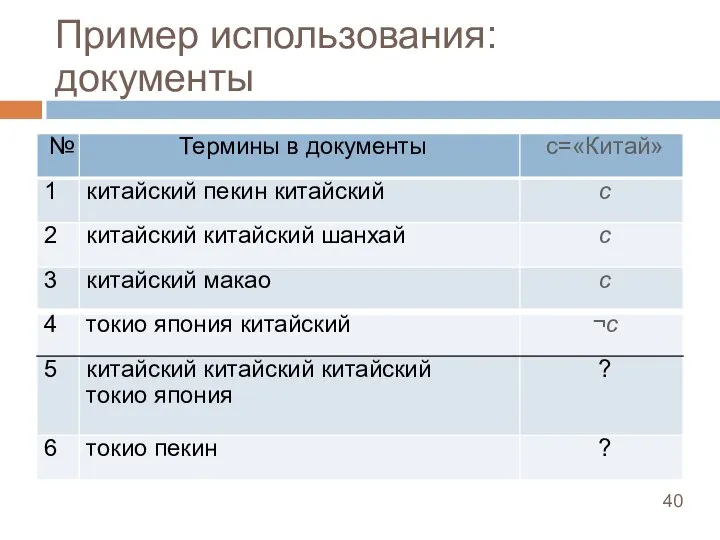
- 40. Пример использования: документы
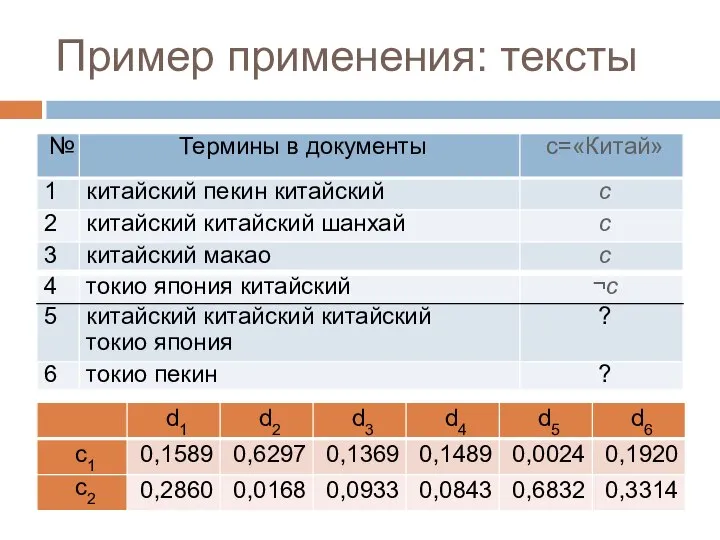
- 41. Пример использования: применение алгоритма Итерация 1. Случайным образом инициализированы μi: μ1=[0,96 0,80 0,42 0,79 0,66 0,85]
- 42. Пример использования: уменьшение цветов изображения Охарактеризуйте рисунки с точки зрения цвета
- 43. Пример использования: уменьшение цветов изображения 64 цвета (случайно) 96615 цветов 64 цвета (K-means)
- 44. Проблемы алгоритма k-средних Не гарантируется достижение глобального минимума суммарного квадратичного отклонения e(D,C) ? Результат зависит от
- 45. Плоский нечеткий алгоритм c-средних (c-means) Является модификацией метода k-средних Входные данные: количество кластеров k степень нечеткости
- 46. Пример применения: тексты
- 47. Оценка качества кластеризации Вычисляются меры двух видов: Внешние меры: сравнение созданного разбиения с «эталонным» анализируется сходство
- 48. Сравнение алгоритмов кластеризации Решение задачи кластеризации принципиально неоднозначно: не существует однозначно наилучшего критерия качества кластеризации количество
- 49. Домашнее задание. Вариант 1 1. Взять выбранный к прошлому разу набор данных 2. Написать программу кластеризации
- 50. Домашнее задание. Вариант 2 Написать программу определения расстояния между текстами 1. Взять несколько текстов (около 10)
- 51. Домашнее задание. Вариант 3 1. Найти готовые средства визуализации многомерных векторов (текстов) 2. Рассказать про них
- 53. Скачать презентацию



































 Презентация на тему Табличные информационные модели (9 класс)
Презентация на тему Табличные информационные модели (9 класс)  Автоматизация фитнес-клубов
Автоматизация фитнес-клубов Создание презентаций. Знакомство с PowerPoint. Раздел 3
Создание презентаций. Знакомство с PowerPoint. Раздел 3 Понятие подпрограмм. Подпрограммы в языке Паскаль
Понятие подпрограмм. Подпрограммы в языке Паскаль Особенности разработки требований к ПО
Особенности разработки требований к ПО Пояснительная записка к дипломному проекту на тему: Разработка протокола телеуправления
Пояснительная записка к дипломному проекту на тему: Разработка протокола телеуправления Анализ подходов решений некоторых практических задач семантической сегментации
Анализ подходов решений некоторых практических задач семантической сегментации Закрытые торговые процедуры
Закрытые торговые процедуры Знакомимся с компьютером
Знакомимся с компьютером Способы прохождения тестирования для поступления на госслужбу
Способы прохождения тестирования для поступления на госслужбу The Berenstain Bears and Too Much Birthday
The Berenstain Bears and Too Much Birthday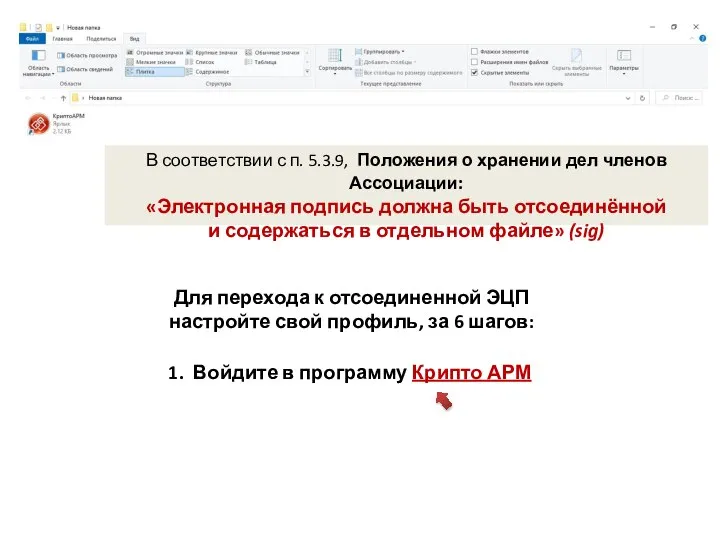 Электронная подпись должна быть отсоединённой и содержаться в отдельном файле
Электронная подпись должна быть отсоединённой и содержаться в отдельном файле ETE2AE+ETZ09E – Operating systems and Computer Networks (Lecture 1)
ETE2AE+ETZ09E – Operating systems and Computer Networks (Lecture 1)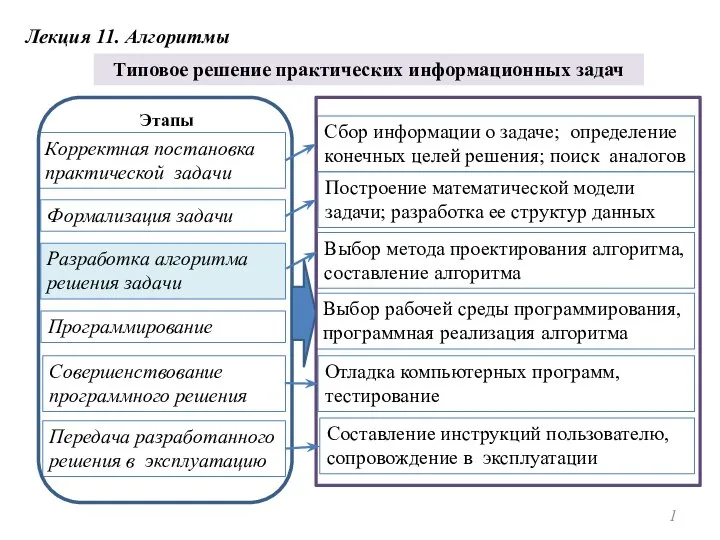 Алгоритмы. Типовое решение практических информационных задач
Алгоритмы. Типовое решение практических информационных задач Продвижение в Ютуб
Продвижение в Ютуб Однотонная заливка светлым цветом
Однотонная заливка светлым цветом Диофантовые уравнения
Диофантовые уравнения Понятие алгоритма. Виды алгоритмов
Понятие алгоритма. Виды алгоритмов Погрузись в мир анимации powerpoint
Погрузись в мир анимации powerpoint Ведение справочника МиС (тема 7)
Ведение справочника МиС (тема 7) Процедура приведения выражений естественного языка к логической форме
Процедура приведения выражений естественного языка к логической форме Оператор if
Оператор if Комплексный интернет-маркетинг. Аналитика. Академия Digital-профессий
Комплексный интернет-маркетинг. Аналитика. Академия Digital-профессий Зефирки((
Зефирки(( Системное программирование. Лекция №6
Системное программирование. Лекция №6 Виписка из счета
Виписка из счета Компьютерные сети. Транспортный уровень. (Тема 6)
Компьютерные сети. Транспортный уровень. (Тема 6) Библиотеки Python
Библиотеки Python