Методы трансляции-1 2022

Формальные языки
Алфавит — конечное множество символов. А = {0,1} — алфавит из двух символов: 0 и 1. Предложения языка – цепочки символов. Множество всех цепочек над алфавитом А обозначается А*.
Определение. Формальный язык L над алфавитом А — это подмножество цепочек из множества всех цепочек алфавита А: L ⊆ А*.

Примеры
Конечный язык можно задать явно: L = {00, 01, 10, 11}. Бесконечный язык описывается либо словами, либо формально, чтобы определить цепочки, входящие в него.
Пример: язык состоит из цепочек над алфавитом {0,1}, начинающихся с единицы, за которой следует чётное число нулей: L0 = {1, 100, 10000, 1000000, …}.
Пример: в язык входят цепочки из 0 и 1 с нечётной длиной и количеством нулей не более 5.
Пример: язык – последовательность натуральных чисел в десятичной записи, разделённых запятыми.

Задачи
Построить формальное описание языка (грамматику);
по описанию языка определить, принадлежит ли ему заданная цепочка (синтаксический анализ);
написать программу, которая проверит принадлежность цепочки языку и преобразует её в цепочку другого языка (транслятор).

Формальные грамматики (1)
Формальной грамматикой называется четвёрка G = (А, V, P, s), где
А — конечное множество терминальных символов (терминалов);
V — конечное множество нетерминальных символов (нетерминалов), V ∩ А = ∅;
P — конечное множество правил вида α → β, где α и β – цепочки на алфавитом А U V, причём в α должен обязательно входить хотя бы один нетерминал;
s ∈ V — начальный символ.

Формальные грамматики (2)
Вывод цепочек языка производится следующим образом:
в правиле α → β цепочка символов α называется левой частью, β — правой;
левая часть должна содержать хотя бы один нетерминал;
правая часть — произвольная цепочка из нетерминалов и терминалов;
если правая часть правила пустая, оно называется пустым или e-правилом).
язык L0 из слайда 3 определяется так:
G0 = ({0, 1}, {s, u}, {s → 1u, s → 1, u → 00u, u → 00}, s)

Формальные грамматики (3)
Обозначения
цепочки из (А U V)* обозначаются строчными греческими буквами;
цепочки из А* обозначаются прописными греческими;
терминалы обозначаются прописными латинскими буквами (B,C, … Z) или цифрами;
нетерминалы обозначаются строчными латинскими (s, t, u, v, … , z).

Формальные грамматики (4)
В процессе вывода строится последовательность цепочек в соответствии с правилами грамматики: каждая следующая цепочка получается из предыдущей заменой в ней подстроки, равной левой части правила, на правую его часть.
Пример — вывод цепочки 10000 в грамматике G0:
s ⇒ 1u ⇒ 100u ⇒ 10000
Для наглядности перенумеруем правила грамматики:
1.s → 1u, 2.s → 1, 3.u → 00u, 4.u → 00;
Вывод: s ⇒ 1u ⇒ 100u ⇒ 10000.
1 3 4

Типы языков по Хомскому
Тип 0 – неограниченные грамматики (рекурсивно вычислимые)
Тип 1 – контекстно-зависимые и неукорачивающие грамматики
Тип 2 – контекстно-свободные (КС) грамматики
Тип 3 – регулярные (автоматные) грамматики
Далее будем рассматривать только грамматики типа 2 и типа 3.

Формальные языки: операции
Формальный язык – множество терминальных цепочек.
Над ними определены теоретико-множественные операции: объединение, пересечение, дополнение, декартово произведение.
Кроме того, определяются ещё две операции: конкатенация и итерация.
Основа первой – конкатенация цепочек α и β, записывается αβ.
Возведение в степень определяется так: α2 = αα, α3 = ααα …
По определению α0 = e (пустая цепочка).

Формальные языки: конкатенация
Конкатенация языков L1 и L2 – множество, содержащее все цепочки, составленные из конкатенаций двух цепочек, первая из L1, вторая — из L2:
L = L1L2 = {αβ | α ∈ L1, β ∈ L2}
Возведение языка в степень: L12 = L1L1, L13 = L1L1L1 ...
Конкатенация и объединение подчиняются тем же законам, что и умножение и сложение, но конкатенация не коммутативна.
Например, {α}({β} U {γ}) = {αβ} U {αγ}, где α, β и γ –цепочки.

Формальные языки: вывод
Множество выводимых цепочек в грамматике (А, V, P, s) рекурсивно задаётся так:
s — выводимая цепочка;
если αγβ — выводимая цепочка и γ → δ ∈ P, то αδβ — выводимая цепочка.
Знак вывода ⇒ означает бинарное отношение на множестве цепочек над алфавитом А U V. Из теории бинарных отношений ⇒+ обозначает транзитивное замыкание отношения, а ⇒* — рефлексивно-транзитивное замыкание.
Для вывода s ⇒ 1u ⇒ 10u можно записать s ⇒* 10u. При записи α ⇒* β говорят, что β выводима из α, а при записи α ⇒ β — непосредственно выводима.

Формальные языки: определение
Язык, порождаемый грамматикой G = (А, V, P, s) —это множество терминальных цепочек, выводимых из начального символа:
L(G) = {Φ ∈ А* | s ⇒* Φ}.
Грамматики, в зависимости от вида правил, порождают разные классы языков. В теории компиляции наибольшую роль играют контекстно-свободные языки, порождаемые КС-грамматиками.
КС-грамматика — грамматика, в которой левые части правил состоят ровно из одного нетерминала.

Формальные языки: нотация
Существует несколько форм записи правил грамматики.
Для правил с одинаковыми левыми частями их правые части называются альтернативами. Эти правила объединяются, правые части разделяются знаком «|»
Пример: правила грамматики G0: s→1u | 1, u→00u | 00
В расширенной форме Бэкуса-Наура (РБНФ) вместо «→» используется «=», в конце правила ставится точка.
Для выделения общих частей в альтернативах служат круглые скобки : s = 1(u | e). u = 00 (u | e).
Для обозначения повторения фрагмента в правой части правила ноль или более раз используются фигурные скобки: s = 1(u | e). u = {00}.

Дерево вывода (1)
Основная задача синтаксического анализа — построение вывода в заданной грамматике. Однако важен не только сам факт существования вывода, но и все промежуточные цепочки вывода.
Рассмотрим грамматику ({с, +, v, =}, {s, expr, term}, P, s) с правилами
s → v = expr
expr → term + term
term → c | v
Вывод для цепочки v = с + v :
s ⇒ v = expr ⇒ v = term + term ⇒ v = с + term ⇒ v = с + v

Дерево вывода (2)
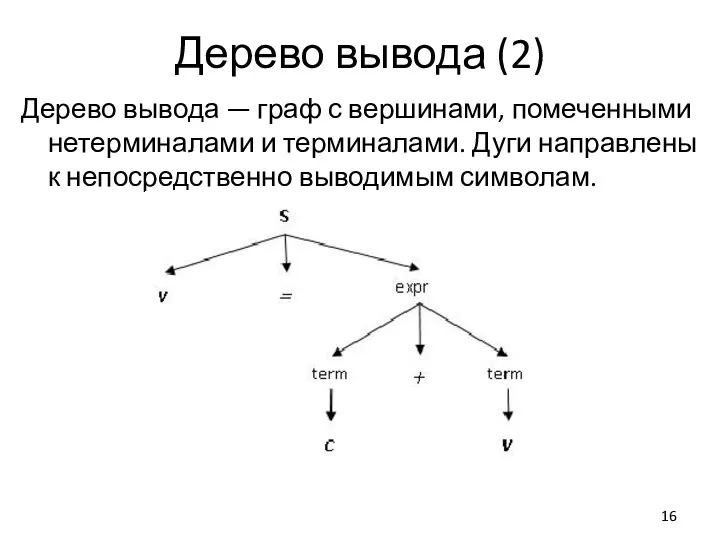
Дерево вывода — граф с вершинами, помеченными нетерминалами и терминалами. Дуги направлены к непосредственно выводимым символам.

Неоднозначный вывод (1)
Рассмотрим условный оператор в языке Паскаль.
oper → if b then oper | if b then oper else oper
Возможны два вывода:
oper ⇒ if b then oper ⇒ if b then if b then oper else oper
oper ⇒ if b then oper else oper ⇒ if b then if b then oper else oper
Из-за неоднозначности в описании языка сделана оговорка: «else относится ко второму if».
В дальнейшем автор языка Н.Вирт исправил эту ситуацию в языках Модула и Оберон.

Неоднозначный вывод (2)
В теории есть понятие неоднозначной грамматики, в которой существует хотя бы одна цепочка, допускающая два различных вывода.
Вывод называется левым (правым), если на каждом шаге применяется правила для самого левого (правого) нетерминала.
Если грамматика однозначна, дерево вывода получается одинаковым независимо от того, производится левый или правый вывод.

Эквивалентные грамматики
Грамматики, которые порождают один и тот же язык, называются эквивалентными.
Пример: грамматика с правилами
s → 1u, u → 00u, u → e
эквивалентна грамматике G0.
Здесь есть пустое правило, неудобное для анализа.
Чтобы его убрать, подставим вместо нетерминала пустого правила пустую цепочку в другие правила.
Пример: s → 1u|1, u → 00u|00
Грамматики, отличающиеся только на правило s → e, называются почти эквивалентными.

Нормальные формы грамматик (1)
Недостижимые нетерминалы не могут появиться ни в одной цепочке, выводимой из начального символа.
Пустые нетерминалы – из которых нельзя вывести ни одной терминальной цепочки.
Процесс преобразования грамматики к эквивалентной без недостижимых и пустых нетерминалов –приведение, полученная грамматика — приведенная.
К понятию приведенной грамматики обычно добавляют условие отсутствия циклических нетерминалов, для которых возможен вывод u ⇒* u.

Нормальные формы грамматик (2)
Грамматика имеет нормальную форму Хомского, если все правые части состоят из двух нетерминалов или из одного терминала.
Грамматика имеет нормальную форму Грейбах, если правые части всех правил (кроме правила s → e) начинаются с терминала, за которым следуют нетерминалы.
Если все эти терминалы разные – грамматика разделённая.
Грамматика не имеет левой рекурсии, если ни для одного нетерминала невозможен вывод u ⇒* uα.

Регулярные грамматики и выражения (1)
Грамматика называется регулярной (автоматной), если все правила имеют вид u → Bv или u → B, где B — терминал, u и v — нетерминалы. Допускается пустое правило для начального символа s → e, но тогда s не должен встречаться в правых частях других правил.
Регулярные грамматики – частный случай КС-грамматик, они порождают класс регулярных языков.

Регулярные грамматики и выражения (2)
Регулярный язык может порождаться и нерегулярной грамматикой.
Пример – грамматика G0 с правилами
{s → 1u, s → 1, u → 00u, u → 00}.
Её легко преобразовать в эквивалентную регулярную грамматику G1, заменив каждое из двух последних правил на два новых:
{s → 1u, s → 1, u → 0x, x → 0u, u → 0y, y → 0}.
Вывод цепочки 10000 в грамматике G1 :
s ⇒ 1u ⇒ 10x ⇒ 100u ⇒ 1000y ⇒ 10000

Регулярные грамматики и выражения (3)
Таким способом можно заменить правила, у которых перед нетерминалом стоит любое число терминалов.
Такие грамматики называются праволинейными.
Регулярный язык порождается и леволинейными грамматиками, их правила имеют вид u ⇒* vΦ или u → B, где Φ – цепочка из терминалов.
Регулярный язык представляет собой регулярное множество, которое может быть определено и без понятия грамматики.

Регулярное множество (определение)
пустое множество ∅ — регулярное множество;
множество из пустой цепочки {ε} — регулярное множество;
множество {a} (атомарное), где a∈A, — регулярное множество;
если L1 и L2 — регулярные множества, то L1 U L2, L1L2 и L1* — регулярные множества.
Последовательно применяя к атомарным множествам операции объединения, конкатенации и итерации (регулярные операции или операциями Клини), можно получить любое регулярное множество.

Регулярное множество (пример)
Язык L0 = {0, 1, 100, 10000, …} строится из атомарных множеств {1} и {0} : {0}U{1}({0}{0})*.
Если убрать фигурные скобки, а знак объединения заменить на «+», получим регулярное выражение:
0+1(00)*.
Приоритет конкатенации выше, чем объединения, приоритет итерации выше, чем у конкатенации, значит, можно не писать лишние скобки.
Пример: выражение 0+100* определяет регулярное множество, в которое входит 0 и цепочки, начинающиеся с 1, за которой следует не менее одного нуля.

Регулярное выражение (1)
С помощью операций можно составлять уравнения из констант и переменных, значения которых –регулярные множества (регулярные выражения).
В уравнении x = ax + b справа записано объединение двух множеств ax и b. Значит, в x входит цепочка из символа b.
Множество ax — это множество цепочек с первым символом a, за которым следует цепочка из x. Значит, ab входит в x.
Если ab входит в x, то aab входит в x. Итак, получим, что множество x = {b, ab, aab, aaab, …}, а выражением, определяющим x, будет a*b.
В исходном уравнении в роли a и b могут быть не отдельные символы, а регулярные выражения.

Регулярное выражение (2)
Представим правила грамматики s → 1u | 1, u → 00u | 00 в виде системы уравнений:
s = 1u + 1
u = 00u + 00
Второе уравнение имеет тот же вид, что и x = ax + b, и оно имеет решение u = (00)* 00. Подставим u в первое уравнение:
s = 1(00)* 00 + 1 = 1((00)* 00 + e) = 1(00)*.
Первое преобразование — 1 выносим за скобки, второе —выражение (00)* 00 + e заменяем эквивалентным и убираем лишние скобки.
Доказано, что подобным образом решаются системы уравнений любой праволинейной грамматики. Другими словами, регулярные грамматики порождают регулярные множества.

Конечный автомат
(определение)
Конечный автомат — это K = (Q, A, δ, q0, F), где
Q — конечное множество состояний;
A — конечное множество входных символов (алфавит);
δ — функция переходов, δ: Q × A → 2Q;
q0 — начальное состояние, q0 ∈ Q;
F — множество конечных состояний, F ⊆ Q.

Конечный автомат
описание (1)
Конечный автомат — это частный случай машины Тьюринга, но нет записи на ленту, головка движется только вправо, результат работы определяется состоянием, в котором он оказался после прочтения цепочки.

Конечный автомат
описание (2)
Конечный автомат — абстрактная машина с лентой, разбитой на клетки, в которых находятся входные символы.
У автомата есть считывающая головка, за один такт работы она передвигается по ленте вправо на клетку.
Автомат находится в одном из состояний. В зависимости от состояния и символа в текущей клетке автомат переходит в новое состояние, которое определено функцией перехода.
Значение функции перехода — подмножество M ⊆ Q. Если для ∀ M: │M│= 1, автомат детерминированный. В противном случае он недетерминированный.

Конечный автомат
конфигурация (1)
В начале работы автомат находится в начальном состоянии, головка стоит на самом левом символе цепочки.
Конфигурация автомата — пара из текущего состояния и непрочитанной части входной цепочки: (q, Φ) . Начальная конфигурация состоит из начального состояния и входной цепочки, заключительная — из конечного состояния и пустой цепочки.
Переход от одной конфигурации к другой обозначается знаком «├», задающим бинарное отношение на множестве конфигураций.

Конечный автомат
конфигурация (2)
Цепочка считается допустимой, если существует хотя бы одна последовательность конфигураций, переводящая начальную конфигурацию в заключительную:
L(K) = {Φ ∈ А* | (q0, Φ) ├* (qk, e), qk ∈ F}.
.

Конечный автомат
пример (1)
Автомат K1 = ({s, u, x, y, t} {0, 1}, δ, s, {t}), где δ:
δ(s, 1) = {u, t}, δ(u, 0) = {x, y},
δ(x, 0) = {u}, δ(y, 0) = {t}.
Будет ли допустима цепочка 10000?
При входной цепочке 10000 автомат должен работать так:
(s,10000) ├ (u,0000) ├ (x,000) ├ (u,00) ├ (y,0) ├ (t,е).
Так как автомат недетерминированный, на первом шаге он мог бы выбрать не состояние u, а состояние t, но тогда он не дочитал бы цепочку до конца.

Конечный автомат
правила построения по грамматике
состояния автомата соответствуют нетерминалам;
добавлено конечное состояние t;
для каждого правила грамматики вида u → Bv установлено значение функции перехода δ(u, B) = v;
для каждого правила грамматики вида u → B установлено значение функции перехода δ(u, B) = t.
Если для некоторой пары (u, B) окажется более одной функции перехода, получится недетерминированный автомат, в противном случае — детерминированный.
Аналогично по конечному автомату можно построить эквивалентную грамматику.

Конечный автомат
задание функции перехода
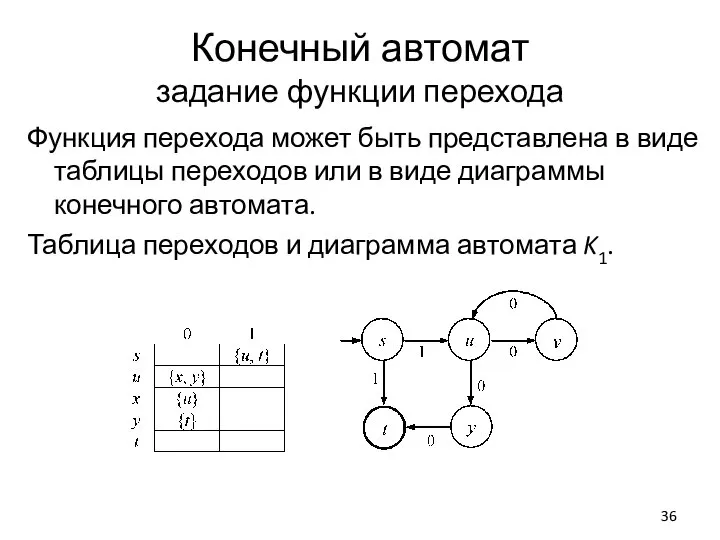
Функция перехода может быть представлена в виде таблицы переходов или в виде диаграммы конечного автомата.
Таблица переходов и диаграмма автомата K1.

Конечный автомат
диаграмма состояний
Диаграмма состояний — ориентированный граф, его вершины помечены состояниями, дуги — входными символами.
Дуга от вершины u к вершине v помечается символом B, если v ∈ δ(u, B).
Построение регулярной грамматики по диаграмме: для каждой дуги от u к v, помеченной символом B, задаем правило вывода u → Bv, а для дуги из u в конечное состояние — правило u → B. Конечные состояния выделяются на графе двойным или жирным кружком, а начальное — небольшой входной стрелкой.

Конечный автомат
диаграмма состояний
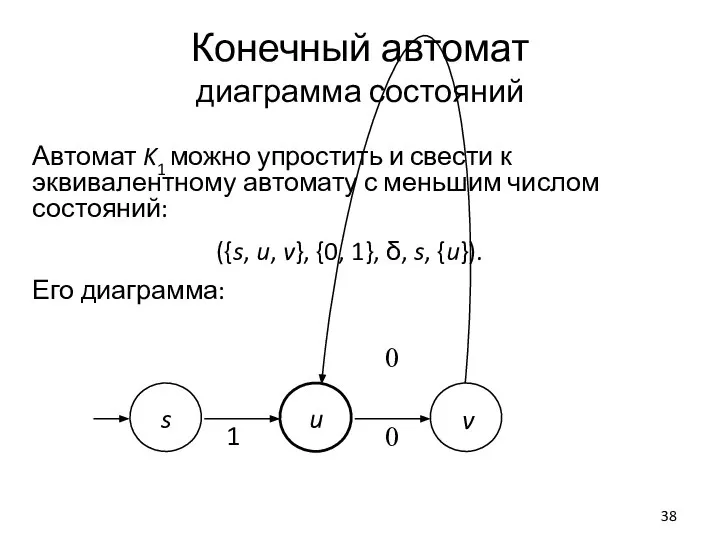
Автомат K1 можно упростить и свести к эквивалентному автомату с меньшим числом состояний:
({s, u, v}, {0, 1}, δ, s, {u}).
Его диаграмма:

Конечный автомат
недетерминированный и детерминированный
При недетерминированном автомате нужно произвести перебор вариантов в тех состояниях, где функция перехода многозначна.
Но для него всегда можно построить эквивалентный детерминированный автомат.
Состояния детерминированного автомата K', который строится по недетерминированному автомату K, представляются подмножествами состояний K, а функция перехода δ' определяется так:
δ'(S, B) = S' для всех S ⊆ Q ,
где S' = {p | δ(q, B) содержит p для некоторого q ∈ S}.

Конечный автомат
детерминированный
Если в автомате K число состояний n , в автомате K' в общем случае может оказаться 2n-1 состояний. Для построения K' проще начинать с начального состояния и последовательно добавлять новые.

Построение ДКА по КА
пример (1)
Построим детерминированный автомат K'1 для автомата K1.
Из s есть переходы по 1 в состояния u и t, тогда в K'1 будет переход по 1 из {s} в {u, t}, т.е. δ'({s}, 1) = {u, t}.
Чтобы построить переход из {u, t} по символу 0, нужно объединить подмножества состояний, в которые K1 переходит по символу 0 из u и из t. То же самое и для символа 1.
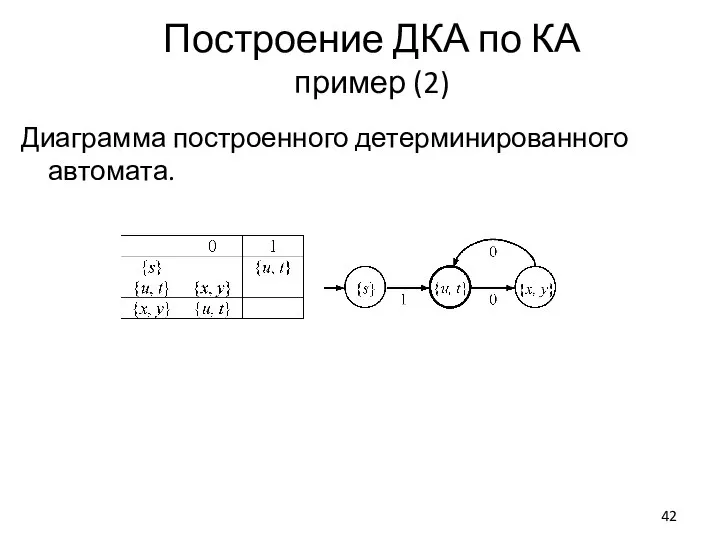
Получаем, что для 1 переходов нет, а δ'({u, t}, 0) = {x, y}. Объединяя подмножества состояний для x и y, получим δ'({x, y}, 0) = {u, t}. Состояние {u, t} уже появлялось, так что построение завершается. Конечным состоянием построенного автомата будет состояние {u, t}.

Построение ДКА по КА
пример (2)
Диаграмма построенного детерминированного автомата.