Содержание
- 2. Нахождение компонент связности В первой строке файла input.txt заданы целые n и m — соответственно число
- 3. Домашнее задание Сколько различных путей есть в дереве с n вершинами? Какое максимальное количество циклов (длиной
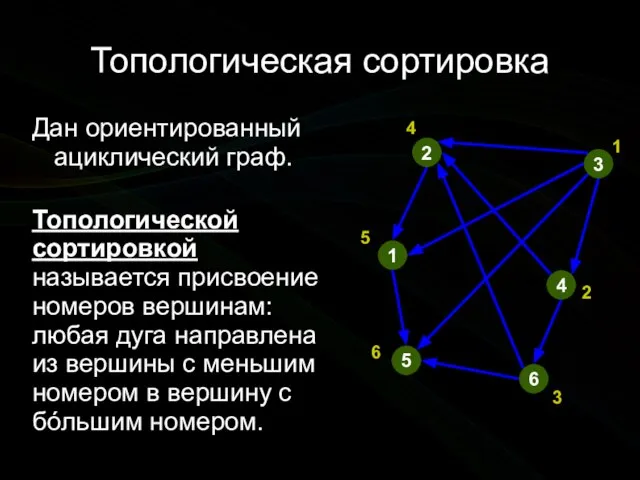
- 4. Топологическая сортировка Дан ориентированный ациклический граф. Топологической сортировкой называется присвоение номеров вершинам: любая дуга направлена из
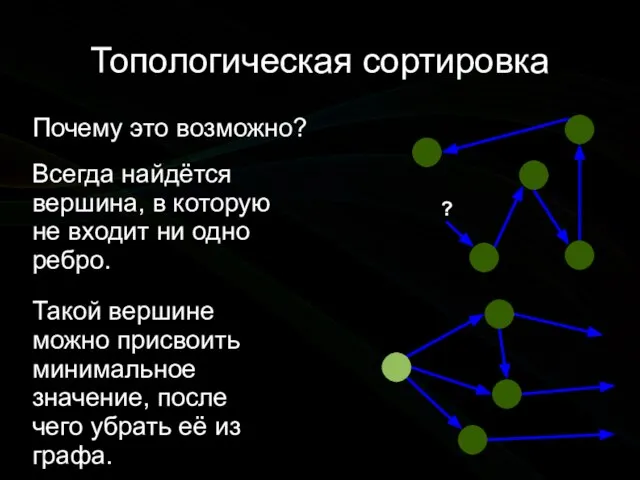
- 5. Топологическая сортировка Почему это возможно? Всегда найдётся вершина, в которую не входит ни одно ребро. Такой
- 6. Топологическая сортировка Как быстро определить вершины, в которые не входит ни одно ребро? Будем хранить входящую
- 7. Топологическая сортировка массив order длины n, order[i] — присвоенный i-й вершине порядковый номер при топологической сортировке;
- 8. Топологическая сортировка В первой строке файла input.txt заданы целые n и m — соответственно число вершин
- 9. Топологическая сортировка В первой строке файла input.txt заданы целые n и m — соответственно число вершин
- 10. Домашнее задание Предприятие «Авто-2010» выпускает двигатели известных во всём мире автомобилей. Двигатель состоит ровно из n
- 11. Домашнее задание Первая строка входного файла details.in содержит число n (1 ≤ n ≤ 10 000)
- 12. Домашнее задание
- 14. Скачать презентацию



![Топологическая сортировка массив order длины n, order[i] — присвоенный i-й вершине порядковый](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/282478/slide-6.jpg)





 Алгоритмы и алгостихи
Алгоритмы и алгостихи Разработка сайта для привлечения молодежи к культуре тюркоязычного коренного народа
Разработка сайта для привлечения молодежи к культуре тюркоязычного коренного народа Презентация на тему Что такое программирование 9 класс
Презентация на тему Что такое программирование 9 класс  Роль материаловедения в графическом дизайне
Роль материаловедения в графическом дизайне Использование интернет-платформ в период дистанционного обучения
Использование интернет-платформ в период дистанционного обучения Мастерская записи и обработки звука Прямой эфир
Мастерская записи и обработки звука Прямой эфир Авторитарный протокол в сетевых боевиках
Авторитарный протокол в сетевых боевиках Статистическая обработка данных
Статистическая обработка данных Моделирование как метод познания
Моделирование как метод познания GET и POST запросы в MVC5
GET и POST запросы в MVC5 Вселенная коллекционера
Вселенная коллекционера Нанотехнологии в информатике
Нанотехнологии в информатике Федеральный мобильный гид по экообъектам, услугам и мероприятиям
Федеральный мобильный гид по экообъектам, услугам и мероприятиям Как правильно сидеть за компьютером
Как правильно сидеть за компьютером Кооперация процессов и основные аспекты её логической организации
Кооперация процессов и основные аспекты её логической организации Привилегии баз данных
Привилегии баз данных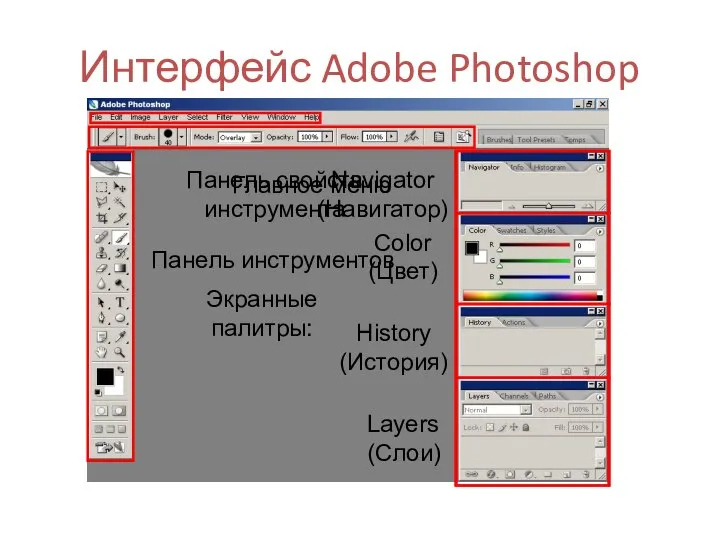 Интерфейс Adobe Photoshop
Интерфейс Adobe Photoshop Классификации ПО. Общие сведения
Классификации ПО. Общие сведения Внешние и внутренние компоненты ПК. Тема 13
Внешние и внутренние компоненты ПК. Тема 13 Курс Базы данных
Курс Базы данных Методы массивов. Метод массива splice
Методы массивов. Метод массива splice Введение в язык С
Введение в язык С Мониторинг деятельности классного коллектива средствами школьного СМИ
Мониторинг деятельности классного коллектива средствами школьного СМИ Debian. Выпуски Debian
Debian. Выпуски Debian Базіка - сервіс чат ботів
Базіка - сервіс чат ботів Двумерные массивы
Двумерные массивы Microprocessor-Based Systems
Microprocessor-Based Systems Возможности текстового процессора WORD
Возможности текстового процессора WORD