Содержание
- 2. Что такое система счисления? Система счисления – это совокупность правил записи чисел с помощью определенного набора
- 3. Что такое система счисления? Системы счисления позиционные непозиционные Значение каждой цифры числа зависит от того, в
- 4. Не позиционные системы счисления Римская система счисления Является непозиционной, т.к. каждый символ обозначает всегда одно и
- 5. Алфавит – набор символов, используемый для обозначения цифр. Основание ПСС – это количество цифр, используемое для
- 6. Позиционные системы счисления Десятичная СС Основание системы – число 10; Алфавит (10 цифр): 0, 1, 2,
- 7. Позиционные системы счисления Двоичная СС Основание системы – 2; Алфавит (2 цифры): 0; 1; Любое двоичное
- 8. Позиционные системы счисления Восьмеричная СС Основание системы – Алфавит ( цифр): Любое восьмеричное число можно представить
- 9. Позиционные системы счисления Шестнадцатеричная СС Основание системы – Алфавит ( цифр): Любое шестнадцатеричное число можно представить
- 10. 1. Перевод чисел из любой системы счисления в десятичную. Для перехода из любой системы счисления в
- 11. Перевод чисел из двоичной системы счисления в десятичную. Для перехода из двоичной системы счисления в десятичную
- 12. Перевод двоичных чисел в десятичную систему ?2??10 Примеры: 102 = 1*2 1 + 0*2 0 =
- 13. Задание № 1: ?2??10 Двоичные числа 1011001, 11110, 11011011 перевести в десятичную систему. проверка
- 14. 2. Перевод чисел из десятичной системы счисления в любую другую Разделить десятичное число на основание системы
- 15. 2. Перевод чисел из десятичной системы счисления в двоичною. Разделить десятичное число на 2. Получится частное
- 16. Перевод ?10 ??2 Примеры: 27 2 13 1 2 6 1 2 3 0 2 1
- 17. Задание № 2: ?10 ??2 Для десятичных чисел 341; 125; 1024 выполни перевод в двоичную систему
- 18. Восьмеричная СС Основание системы – 8; Содержит 8 цифр: 0; 1; 2; 3; 4; 5; 6;
- 19. Правило перевода из десятичной системы счисления в восьмеричную Разделить десятичное число на 8. Получится частное и
- 20. Перевод ?10 ??8 132 8 16 4 8 2 0 13210 = 8
- 21. Задание № 3: ?10 ??8 Десятичные числа 421, 5473, 1061 перевести в восьмеричную систему. проверка
- 22. Правило перехода из восьмеричной системы счисления в десятичную. Для перехода из восьмеричной системы счисления в десятичную
- 23. Задание № 4: ?8??10 Восьмеричные числа 41, 520, 306 перевести в десятичную систему. проверка
- 24. ШестнадцатеричнаяСС Основание системы – 16; Содержит 16 цифр: от 0 до 9; A; B; C; D;
- 25. Правило перехода из десятичной системы счисления в шестнадцатеричную Разделить десятичное число на 16. Получится частное и
- 26. Примеры: ?10??16 335 16 20 1 16 1 4 33510 = 16 5 F
- 27. Задание № 5: ?10??16 Десятичные числа 512, 302, 2045 перевести в шестнадцатеричную систему. проверка
- 28. Правило перехода из шестнадцатеричной системы счисления в десятичную. Для перехода из шестнадцатеричной системы счисления в десятичную
- 29. Задание № 6: ?16??10 Шестнадцатеричные числа B5, A28, CD перевести в десятичную систему. проверка
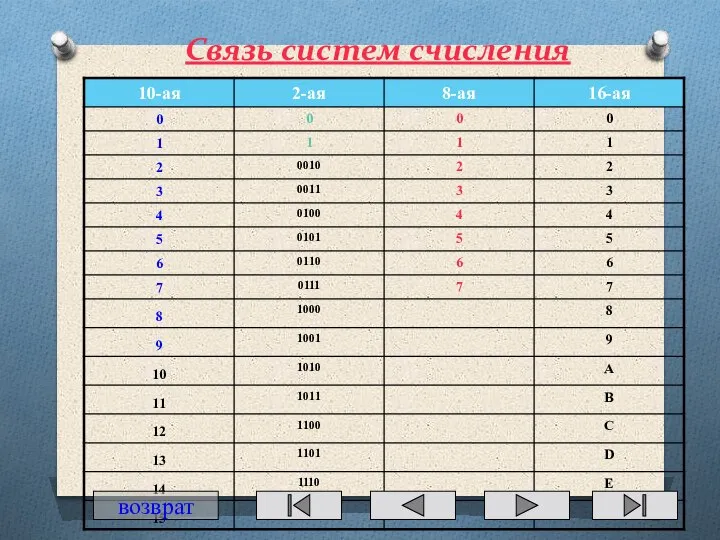
- 30. Связь систем счисления возврат
- 31. Правило перехода из двоичной системы счисления в восьмеричную Разбить двоичное число на классы справа налево по
- 32. Задание № 7: ?2??8 Двоичные числа 10101111, 11001100110 перевести в восьмеричную систему проверка
- 33. Правило перехода из восьмеричной системы счисления в двоичную ?8??2 Каждую восьмеричную цифру заменить двоичным классом по
- 34. Задание № 8: ?8??2 Восьмеричные числа 26, 702, 4017 перевести в двоичную систему. проверка
- 35. Правило перехода из двоичной системы счисления в шестнадцатеричную ?2??16 Разбить двоичное число на классы справа налево
- 36. Задание № 9: ?2??10 Двоичные числа 10101111, 11001100110 перевести в шестнадцатеричную систему проверка
- 37. Правило перехода из шестнадцатеричной системы счисления в двоичную ?16??2 Каждую шестнадцатеричную цифру заменить двоичным классом по
- 38. Задание № 10: ?16??2 Шестнадцатеричные числа C3, B096, E38 перевести в двоичную систему. проверка
- 39. Задания для домашней работы Для каждого из чисел: 12310, 45610 выполнить перевод: 10→2, 10 → 8,
- 40. Ответы к заданию № 1
- 41. Ответы к заданию №2
- 42. Ответы к заданию №3
- 43. Ответы к заданию №4
- 44. Ответы к заданию №5
- 45. Ответы к заданию №6
- 46. Ответы к заданию №7
- 47. Ответы к заданию №8
- 48. Ответы к заданию №9
- 49. Ответы к заданию №10
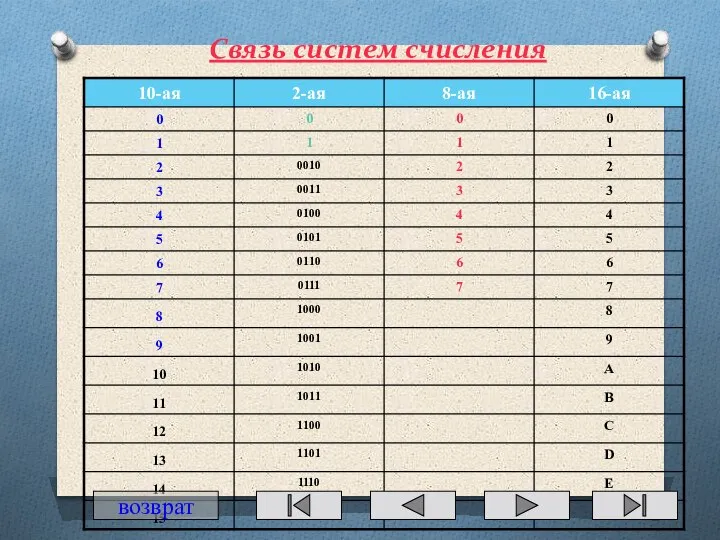
- 50. Связь систем счисления возврат
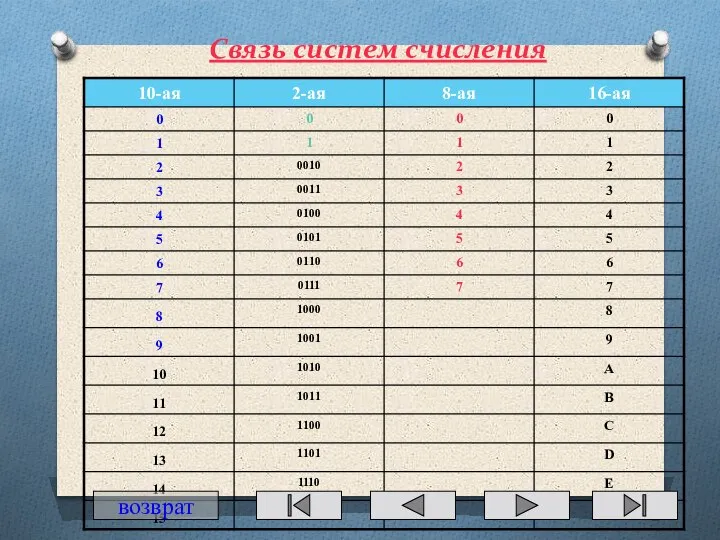
- 51. Связь систем счисления возврат
- 53. Скачать презентацию















































 Разработка полноценной системы управления в фармацевтических предприятиях. Microsoft Word. Microsoft excel
Разработка полноценной системы управления в фармацевтических предприятиях. Microsoft Word. Microsoft excel Двоичное кодирование. Информатика и ИКТ
Двоичное кодирование. Информатика и ИКТ Pie chart
Pie chart Архитектура и ПО сетевых устройств. Основы сетевых технологий
Архитектура и ПО сетевых устройств. Основы сетевых технологий Технология разработки баз данных
Технология разработки баз данных Повторение Питон
Повторение Питон Информатика. Введение
Информатика. Введение Интернет-источники по географии
Интернет-источники по географии Контент. Работа с текстом
Контент. Работа с текстом 30 сентября - профессиональный праздник всех пользователей и работников Интернет-индустрии. Международный День Интернета
30 сентября - профессиональный праздник всех пользователей и работников Интернет-индустрии. Международный День Интернета Создание сообщества
Создание сообщества Інтерактивний веб-сайт з використанням технологій доповненої реальності
Інтерактивний веб-сайт з використанням технологій доповненої реальності Легко создавайте свои собственные видео
Легко создавайте свои собственные видео GRandapp. Смартфон - это просто
GRandapp. Смартфон - это просто Регистрация студента в ЭИОС
Регистрация студента в ЭИОС Инструментальные средства моделирования сложных систем
Инструментальные средства моделирования сложных систем Системы счисления
Системы счисления Управление исполнителями. Циклы с условием
Управление исполнителями. Циклы с условием Мотивация оператора. Договор присоединения
Мотивация оператора. Договор присоединения Презентация на тему Электронный документооборот
Презентация на тему Электронный документооборот  Информационные модели: системы и структуры данных
Информационные модели: системы и структуры данных Дизайн RedOS 8.0
Дизайн RedOS 8.0 Решение задачи о ферзях. Проект С++
Решение задачи о ферзях. Проект С++ Реализация алгоритмов ветвления в среде программирования
Реализация алгоритмов ветвления в среде программирования Основы построения моделирующего алгоритма в среде GPSS World
Основы построения моделирующего алгоритма в среде GPSS World E-learning infographics
E-learning infographics Системы рекомендаций
Системы рекомендаций Blogger YouTube
Blogger YouTube