соседнего старшего разряда.
Таким образом, каждый разряд имеет вес, равный степени 10.
Например, в записи числа 343.32 цифра 3 повторена три раза, при этом самая левая цифра 3 означает количество сотен (ее вес равен 102); цифра 3. стоящая перед точкой, означает количество единиц (ее вес равен 100 ), а самая правая цифра 3 — количество десятых долей единицы (ее вес равен 10-1), так что последовательность цифр 343.32 представляет собой сокращенную запись выражения :
3x102 + 4x101+3x100 + 3x10-1 + 2x10-2.
Десятичная запись любого числа X в виде последовательности цифр:
аnаn-1..а1aоа-1...ат...
основана на представлении этого числа в виде полинома:
Х = аn10n + аn-110n-1+... +a1 101+a0100+a-110-1+...+a-m10-m...,
Десятичная позиционная система счисления








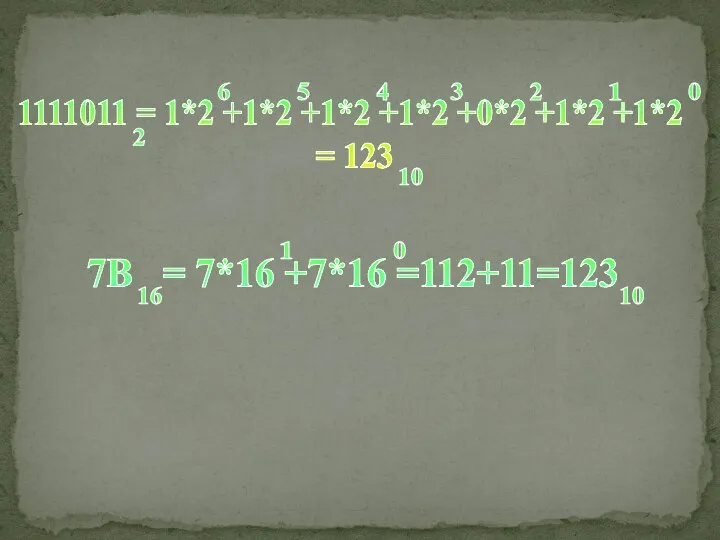


 WB Транзит
WB Транзит Генеративные состязательные сети
Генеративные состязательные сети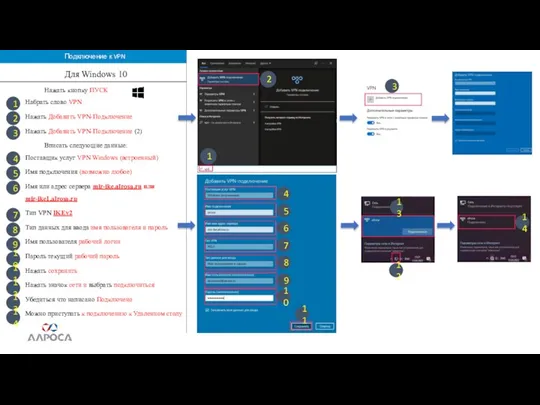 Подключение к VPN Для Windows 10
Подключение к VPN Для Windows 10 Компьютерные вирусы и антивирусные программы
Компьютерные вирусы и антивирусные программы Test nr 18
Test nr 18 Визуализация информации в текстовых документах
Визуализация информации в текстовых документах Неделя информатики
Неделя информатики Никнеймы. Что они могут рассказать о человеке?
Никнеймы. Что они могут рассказать о человеке? Системы объектов
Системы объектов Программирование на языке С++
Программирование на языке С++ Презентация на тему Технологии обработки числовых данных
Презентация на тему Технологии обработки числовых данных  Беспроводные сети
Беспроводные сети Для тестеров
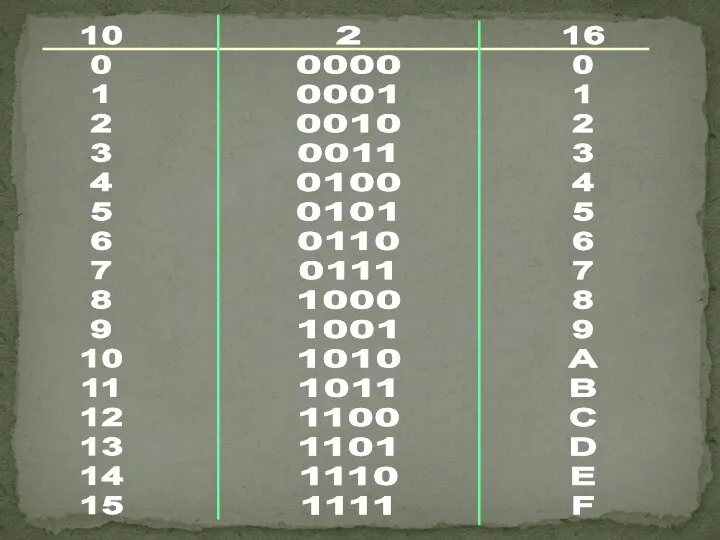
Для тестеров Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики Создание и использование ЦОР на уроках информатики с целью формирования у учащихся информационно-коммуникационной компетентности
Создание и использование ЦОР на уроках информатики с целью формирования у учащихся информационно-коммуникационной компетентности Примеры социальных сетей
Примеры социальных сетей Информационная безопасность. Тема 6
Информационная безопасность. Тема 6 Сайт PowerPointBase.com
Сайт PowerPointBase.com Евгений Казанцев. Instagram
Евгений Казанцев. Instagram Акция Снова в школу
Акция Снова в школу Презентация на тему Создание презентаций
Презентация на тему Создание презентаций  Внедрение СМА в ООО Газпромнефть-Оренбург
Внедрение СМА в ООО Газпромнефть-Оренбург Кодирование информации в компьютере
Кодирование информации в компьютере Бизнес план интернет магазина Leki-shop
Бизнес план интернет магазина Leki-shop Преподаватель и студент в цифровом образовательном пространстве: опыт успешного взаимодействия
Преподаватель и студент в цифровом образовательном пространстве: опыт успешного взаимодействия Электронно-цифровая подпись
Электронно-цифровая подпись Условный оператор
Условный оператор Системы программирования и прикладное программное обеспечение
Системы программирования и прикладное программное обеспечение