Содержание
- 2. Истории математики более 3 тысяч лет. Народы разных стран и разных эпох способствовали развитию математики. Арабские
- 3. Развитие математики, требовалось для государственного управления, строительства, торговли и ремесел. Международные связи, осуществляемые с помощью длительных
- 4. У мусульманских народов VII – XV веков было три математических школы: Багдадская Самаркандская Марагинская
- 5. Марагинская математическая школа Насирэддин Туси был первым руководителем марагинской математической школы. В этой школе, велась большая
- 6. Улугбек Тарагай
- 7. Багдадская научная школа Первый научный центр – Багдад. В конце 8 – нач. 9 вв. в
- 8. Арабский язык – язык средневековой науки! Работа у арабских ученых над греческими трактатами обычно состояла из
- 9. Арифметический трактат Первая страница латинского текста рукописи, XIV в. В арифметическом трактате: Объясняется принцип записи чисел
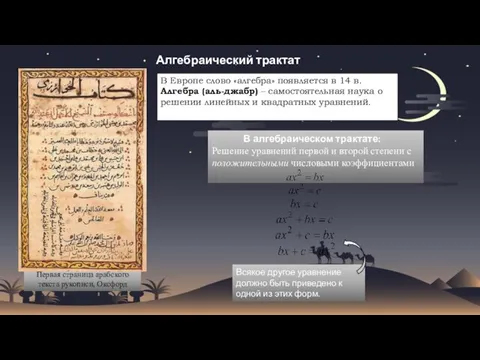
- 10. Алгебраический трактат Первая страница арабского текста рукописи, Оксфорд В алгебраическом трактате: Решение уравнений первой и второй
- 11. Первым знаменитым ученым багдадской школы был Мухаммед ал-Хорезми. Сохранились 5 работ ал-Хорезми, частично переработанные, из которых
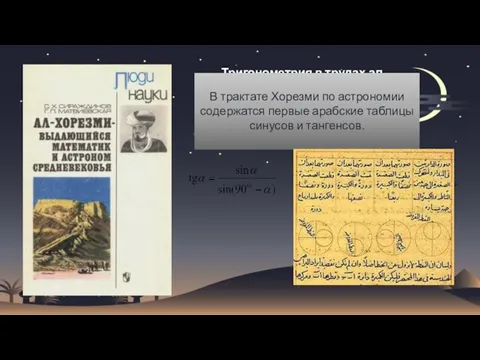
- 12. Тригонометрия в трудах ал-Хорезми В трактате Хорезми по астрономии содержатся первые арабские таблицы синусов и тангенсов.
- 13. Братья Бану Муса Мухаммад, Ахмад и ал-Хасан — выдающиеся учёные арабского Халифата, занимавшиеся геометрией, астрономией и
- 14. Аль-Бируни Энциклопедист, создал фундаментальные работы по математике, астрономии, ботанике, географии, и другим наукам. Ученый широко применял
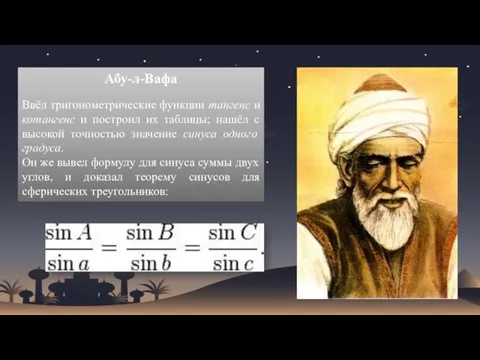
- 15. Абу-л-Вафа Ввёл тригонометрические функции тангенс и котангенс и построил их таблицы; нашёл с высокой точностью значение
- 16. Омар Хайам - Создал геометрическую теорию решения уравнений 3-й степени - Дал новую классификацию 25 типов
- 17. Вывод: Математика стран ислама оказала исключительное влияние на развитие математики как на Востоке, так и на
- 19. Скачать презентацию













 Прогулки по Ишиму
Прогулки по Ишиму Презентация на тему Эпоха великих реформ
Презентация на тему Эпоха великих реформ  Город Ярославль
Город Ярославль Селение Хумалаг
Селение Хумалаг Казанский собор
Казанский собор Герои труда
Герои труда Предметный мир человека
Предметный мир человека 800 лет Нижнему Новгороду
800 лет Нижнему Новгороду Великая французская революция
Великая французская революция Россия в XVII веке
Россия в XVII веке 15 февраля - День памяти воинов-интернационалистов. Память о них будет жить вечно
15 февраля - День памяти воинов-интернационалистов. Память о них будет жить вечно Птицы смерти в зените стоят. Кто идет выручать Ленинград?
Птицы смерти в зените стоят. Кто идет выручать Ленинград? Modern (post-colonial) history of Egypt
Modern (post-colonial) history of Egypt Научно-техническая революция и мировое хозяйство
Научно-техническая революция и мировое хозяйство Борский ветеран
Борский ветеран Зоологический сад Санкт - Петербурга. К 75 - летию Победы (часть 4)
Зоологический сад Санкт - Петербурга. К 75 - летию Победы (часть 4) 23 февраля
23 февраля Причины, повод и начало Первой мировой войны
Причины, повод и начало Первой мировой войны Война глазами деда
Война глазами деда Россия в 1917 г
Россия в 1917 г Презентация на тему Культурна-нацыянальнае жыццё рэспублікі
Презентация на тему Культурна-нацыянальнае жыццё рэспублікі  7 клас 07.10 (1) (1)
7 клас 07.10 (1) (1) Запас прочности
Запас прочности Братья Ткачёвы
Братья Ткачёвы Храм Воскресения Христова в Старой Ольшанке – жемчужина церковной архитектуры
Храм Воскресения Христова в Старой Ольшанке – жемчужина церковной архитектуры Формирование княжеской власти на Руси
Формирование княжеской власти на Руси Первая мировая война Статистические данные и схемы к уроку истории
Первая мировая война Статистические данные и схемы к уроку истории Сокровища бывшей гимназии
Сокровища бывшей гимназии