Компланарные векторы

Определение компланарных векторов
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также компланарны.

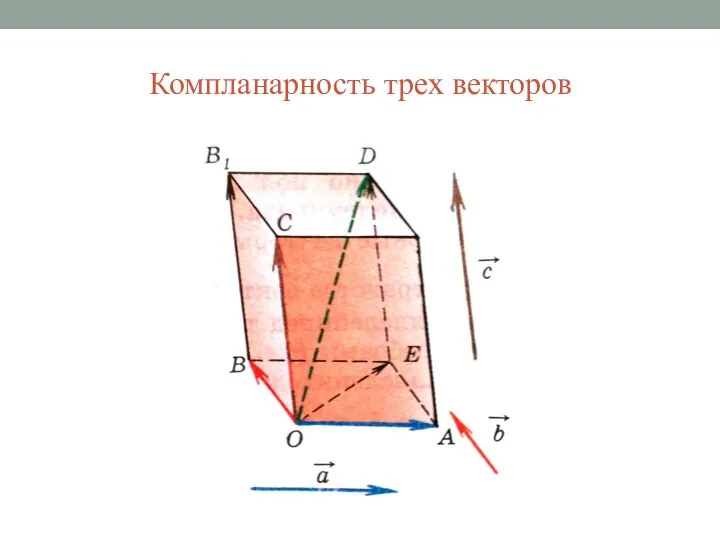
Компланарность трех векторов

Признак компланарности трех векторов
Если вектор с можно разложить по векторам а и b, т. е. представить в виде
,
где х и у - некоторые числа, то векторы а, b и с компланарны.

Правило параллелепипеда
Пусть a, b и с – некомпланарные векторы. Отложим от произвольной точки О пространства векторы
и построим параллелепипед так, чтобы отрезки ОА, ОВ и ОС были его ребрами. Тогда диагональ OD этого параллелепипеда изображает сумму векторов a, b и с:

Разложение вектора по трем
некомпланарным векторам
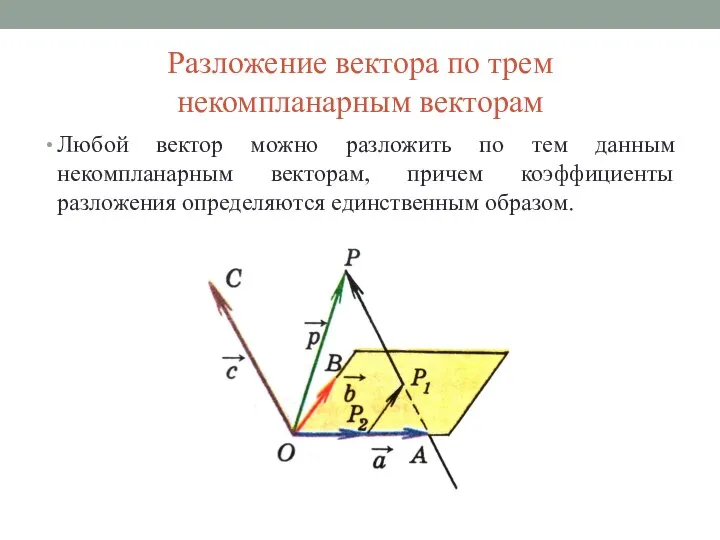
Любой вектор можно разложить по тем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.