Содержание
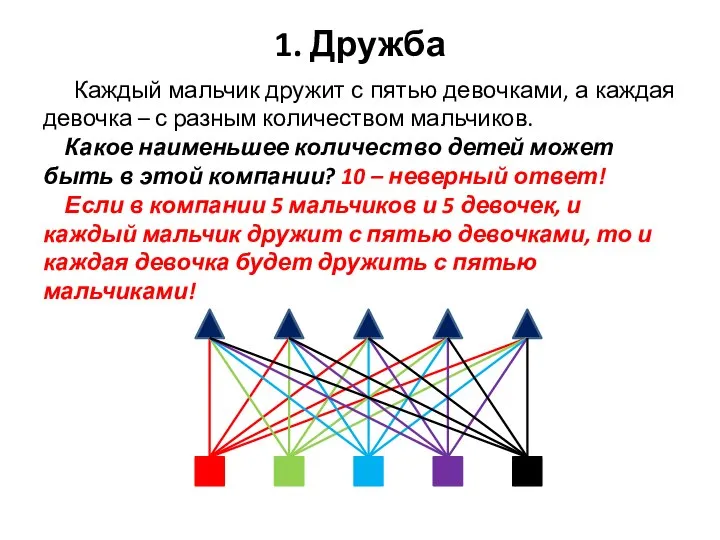
- 2. 1. Дружба Каждый мальчик дружит с пятью девочками, а каждая девочка – с разным количеством мальчиков.
- 3. 1. Дружба Каждый мальчик дружит с пятью девочками, а каждая девочка – с разным количеством мальчиков.
- 4. Каждый мальчик дружит с одним и тем же количеством девочек. Каждая девочка дружит с разным количеством
- 5. Каждый мальчик дружит с одним и тем же количеством девочек. Каждая девочка дружит с разным количеством
- 6. Общее количество «дружб» = 1+2+3+4+…+m S + S = m × (m +1 ); S =
- 7. Каждый мальчик дружит с одним и тем же количеством девочек. Каждая девочка дружит с разным количеством
- 8. Каждый мальчик дружит с одним и тем же количеством девочек. Каждая девочка дружит с разным количеством
- 9. Каждый мальчик дружит с одним и тем же количеством девочек. Каждая девочка дружит с разным количеством
- 10. Каждый мальчик дружит с одним и тем же количеством девочек. Каждая девочка дружит с разным количеством
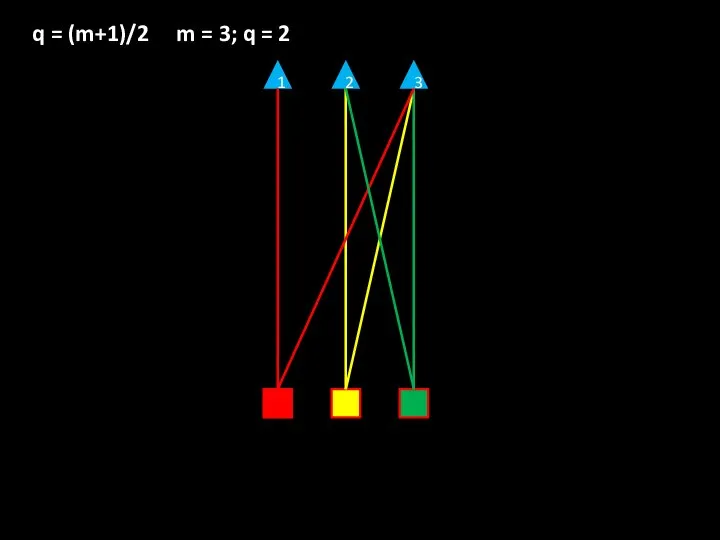
- 11. 1 2 3 q = (m+1)/2 m = 3; q = 2
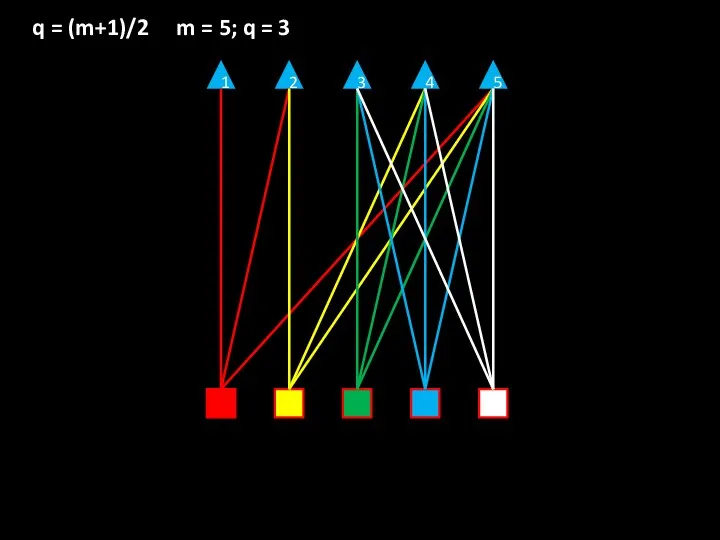
- 12. 1 2 3 4 5 q = (m+1)/2 m = 5; q = 3
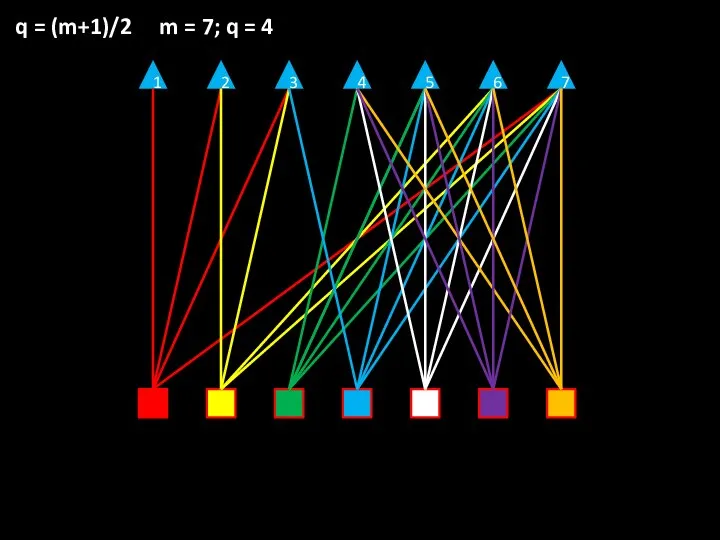
- 13. 1 2 3 4 5 6 7 q = (m+1)/2 m = 7; q = 4
- 15. Скачать презентацию








 Злые Люди. Кто это такой и как не стать таким!
Злые Люди. Кто это такой и как не стать таким! Компания Семивер. Тактильная напольная разметка
Компания Семивер. Тактильная напольная разметка Милосердие и сострадание
Милосердие и сострадание Всероссийские форумы Росмолодежи
Всероссийские форумы Росмолодежи Влияние автотранспорта на окружающую среду и здоровье населения
Влияние автотранспорта на окружающую среду и здоровье населения Типология обществ
Типология обществ Человек и общество. Задания 1 части
Человек и общество. Задания 1 части “Мулоқот кўникмалари” тренинги
“Мулоқот кўникмалари” тренинги Добровольческий проект Отражение победы. Помощь ветеранам
Добровольческий проект Отражение победы. Помощь ветеранам Исследовательская работа по теме: «Об истории празднования Масленицы на Руси» Подготовили: обучающиеся 1 класса МБОУ «ОО Курская
Исследовательская работа по теме: «Об истории празднования Масленицы на Руси» Подготовили: обучающиеся 1 класса МБОУ «ОО Курская Классный руководитель: Классный руководитель: Устюжанина Мария Александровна Выполнили учащиеся 4В класса: Яцуценко Данила Ца
Классный руководитель: Классный руководитель: Устюжанина Мария Александровна Выполнили учащиеся 4В класса: Яцуценко Данила Ца Семья в воспитании нравственности
Семья в воспитании нравственности Клуб КИК профсоюзного комитета РКК Энергия
Клуб КИК профсоюзного комитета РКК Энергия Презентация на тему 9 Мая (2 класс)
Презентация на тему 9 Мая (2 класс)  Презентация на тему Духовно-нравственное образование как ключевой элемент Национальной идеи России
Презентация на тему Духовно-нравственное образование как ключевой элемент Национальной идеи России  Презентация на тему "Почему демократическому государству нужны выборы?"
Презентация на тему "Почему демократическому государству нужны выборы?"  Межличностные отношения
Межличностные отношения Презентация на тему Карнавал в Германии
Презентация на тему Карнавал в Германии  Обществознание. 8 класс. Учитель Гришакина О.П. Электронные материалы урокам. 5-й урок. Тип урока – урок изучения нового материла Тема урока: «СОЦИАЛЬНЫЙ ПРОГРЕСС И РАЗВИТИЕ ОБЩЕСТВА» На дом: §4, эссе «Возможен ли социальный прогресс в нашем класс
Обществознание. 8 класс. Учитель Гришакина О.П. Электронные материалы урокам. 5-й урок. Тип урока – урок изучения нового материла Тема урока: «СОЦИАЛЬНЫЙ ПРОГРЕСС И РАЗВИТИЕ ОБЩЕСТВА» На дом: §4, эссе «Возможен ли социальный прогресс в нашем класс  Наш отряд Тимуровцы
Наш отряд Тимуровцы Презентация на тему Хранители предания в религиях мира
Презентация на тему Хранители предания в религиях мира  Презентация на тему "Христианская семья"
Презентация на тему "Христианская семья"  Через нос проходит в грудь И обратный держит путь Он невидимый: и всё же Без него мы жить не можем.
Через нос проходит в грудь И обратный держит путь Он невидимый: и всё же Без него мы жить не можем. Презентация на тему Безработица. Виды безработицы
Презентация на тему Безработица. Виды безработицы  Презентация на тему Человек и его деятельность (6 класс)
Презентация на тему Человек и его деятельность (6 класс)  Презентация на тему Сделаем мир добрее (2 класс)
Презентация на тему Сделаем мир добрее (2 класс)  Презентация на тему Значение лесов
Презентация на тему Значение лесов  Леонид Андреев «Иуда Искариот» «Я хочу писать об Иуде… у меня есть СВОЯ идея…»
Леонид Андреев «Иуда Искариот» «Я хочу писать об Иуде… у меня есть СВОЯ идея…»