Муниципальное общеобразовательное учреждение Гимназии 2 «Квантор». Секция математики. Проект по алгебре. Тема: «Эффективные пути

Эффективные пути решений неравенств. Метод замены множителей.
Все неравенства с одной переменной, которые рассматриваются в школе или предлагаются в конкурсных заданиях вступительных экзаменов, имеют одну и ту же структуру ответа промежуток или объединение промежутков.
Легко усваиваемыми учащимися неравенствами являются рациональные неравенства, решение которых рассмотрено в школьных учебниках и многочисленных пособиях для поступающих в вузы. Поэтому естественным признать желание свести решение неравенств повышенной сложности к решению рациональных неравенств. Оказывается, достаточно широкий класс неравенств подобную попытку допускает.
Рассмотрим применение метода замены множителей.

Содержание:
1.Замена знакопостоянных множителей.
2.Замена множителей с модулем.
3.Замена множителей с иррациональными выражениями.

1. Замена знакопостоянных множителей.
1) Метод замены множителей применяется в неравенствах вида:
V 0
Символ «V» означает один из четырех возможных знаков неравенства:
<; ≤; ≥; >.
2) Основная идея метода замены множителей состоит в замене любого множителя M на знакосовпадающей с ним и имеющий одни и те же корни (в области существования всех множителей) множитель L.
Замечание. Преобразованное таким образом неравенство всегда равносильно исходному в области существования последнего.
Предупреждение. Указанная замена возможна только тогда, когда заменяемый множитель находится в числителе или знаменателе дроби, которая сравнивается с нулем.

Пример 1.
(МГУ факультет вычислительной математики и кибернетики, задача №1 из пяти)
Решите неравенство:
(X2 – 9)
≥0
Решение:
В неравенстве есть знакопостоянный множитель
который провоцирует следующее неправильное решение. Так как произведение двух множителей (X2 – 9) и
неотрицательно, и второй множитель неотрицателен, то и первый множитель (X2 – 9) должен быть неотрицательным. Поэтому решение неравенства определяется следующей системой:
│X│ ≥ 3
-3
3
x

2) X2 – X – 2 = 0
3)
X
(-∞; -3]
[3; +∞)
-3
-1
2
3
x
Полученный ответ не содержит X=2 и X=-1, которые были потерянны в результате решения.
Теперь приведем одно из правильных решений.
Корень из трехчлена в области допустимых значений всегда совпадают по знаку с этим трехчленом, поэтому имеем:
(X2 – 9)
≥0

-3
-1
2
3
x
x
-1
2
X
(-∞; -3]
X=-1
X=2
(-∞; -3]
[3; +∞); -1; 2.
X=3
Ответ: X
Замена множителя
на X2 – X – 2 позволило перейти от иррационального неравенства к стандартному рациональному неравенству в области допустимых значений исходного неравенства.
2. Замена множителей модулем.
Опорная информация, позволяющая указать удобные замены, заключается в двух основных свойствах модуля: │m│ =m │m│≥0 для всех m, а так же в монотонном возрастании на множестве неотрицательных чисел функции
Типы замен:
y=t
(
)
(
)(
)
(
)
(
)(
)
(
)
(
)

(
)
(
)(
)
(
)
(
)(
)
Удобно указать частные случаи замен:
- (ax2+bx+c)
(
-ax2-bx-c) (
+ax2+bx+c)
a>0 и D≤0
(ax2+bx+c-
)
(ax2+bx+c+)(ax2+bx+c-
)
Пример 2.
Решите неравенство:
Решение:
Каждый множитель как в числителе так и в знаменателе есть разность неотрицательных чисел. Поэтому заменяя их на разность квадратов, получим равносильное неравенство в области значения.

Далее, пользуясь свойством модуля │m│ =m и раскладывая на множитель разности квадратов, получим.
–X2+X-6=0 2) X2+X+2=0
D=1-24<0 D=1-8<0
-X2+X-6<0 X2+X+2>0
При X
/R При X
/R

Заменим первый множитель на (-1); второй – на множитель (1)
Получим:
Следует:
-3
-2
1
5
X
Вернемся к системе:

Ответ: ( - 3; - 2 )
[ 2; 5 )
Пример 3.
Решить неравенство:
Решение:

1) –X2+2X+8=0
X2-2X-8=0
2)2X2+2>0
При X
/R
Заменим (1)
3)2X2+6>0
При X
/R
Заменим (1)
4)X2-X-2=0

-9
-2
-1
0
1
2
4
X
X
(-2; -1)
(0; 1)
(2; 4)
Ответ: (-2; -1)
(0; 1)
(2; 4)
Пример 4.
В этом неравенстве уже нельзя множители ( ) и (│X+14│-2X) рассматривать как разности неотрицательных чисел, так как выражения 3x и 2x в области допустимых значений ( т.е x≥-10) могут принимать как положительные так и отрицательные значения.
Однако, если область допустимых значений исходного неравенства разбить на два промежутка -10≤x≤0 и x>0 (точка x=0 есть точка смены знака выражений 3x и 2x, то заметим, что на промежутке -10≤x≤0 имеем произведение двух положительных чисел, и поэтому неравенство ложно, а при x>0 каждый множитель есть разность двух неотрицательных чисел, а следовательно можно воспользоваться методом замены множителей.
Итак.

(
)(|
+14|-2x)<0
А это ложно;
При X>0
1) X+1>0
2) 3X+14>0

0
10/9
14
X
X
(10/9; 14)
Ответ: (10/9; 14)
Пример 4.
Наводит на мысль, как действовать в произвольной подобной ситуации: область допустимых значений неравенства разбить на промежутки знакопостоянства выражений, которые необходимо возводить в квадрат, чтобы воспользоваться методом замены множителей; далее на каждом из полученных промежутков решать исходное неравенство и полученные ответы объединить.
Рассмотрим пример.
Пример 5.
Решить неравенство:
1) О.Д.З.

-18
-1
1
X
X
[-18; -1]
[1; +∞)
2)О.Д.З. нулями выражений (2-x) и (x2-2x) разбивается на три промежутка.
-18
-1
0
1
2
X
1. -18≤x≤-1; 2.1≤x≤2; 3.x≥2.
1.Решаем неравенство на (1) промежутке.
-18≤x≤-1
Заметим: 1)
(заменим (1))

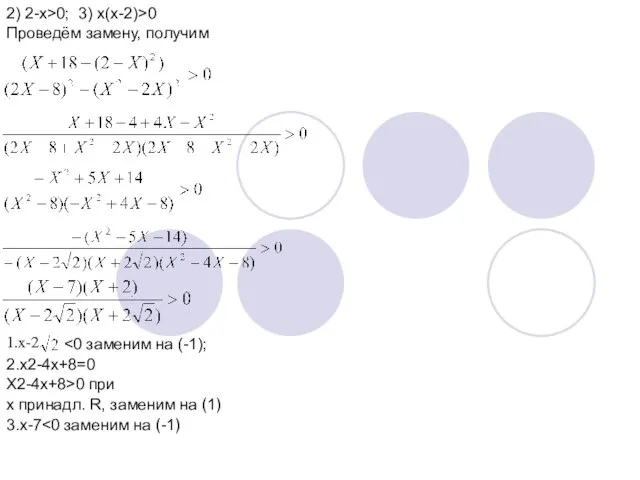
2) 2-x>0; 3) x(x-2)>0
Проведём замену, получим
1.x-2
<0 заменим на (-1);
2.x2-4x+8=0
X2-4x+8>0 при
x принадл. R, заменим на ﴾1﴿
3.x-7<0 заменим на ﴾-1﴿

-18
-2
-2
-1
x
2.Рамотрим неравенство на втором промежутке x принадлежит [1;2].
1.x>0
2.x﴾x-2﴿≤0,
след. |2x-8|-﴾x-2﴿>0, заменим на
﴾1﴿.
3.2-x>0,
Тогда:

X2-5X-14>0
-2
1
2
7
X
3.Решаем неравенство на третьем промежутке x≥2
При x≥2
1. 2-x=0 на (-1)
2.
3.x>0
4.x(x-2)≥0
Получим

(-X2+4X-8)(X2-8)<0
(X2-4X+8)(X-2
)(X+2
)>0
X2-4x+8>0, при x принадлеж. IR (Д>0).
Тогда
5.Объединим ответы, полученные в разобранных трёх случаях.

-18
-2
-1
2
X
Ответ: [-18;- 2
﴿*﴾-2;-1]*[ 2
;+∞﴿.

Вывод:
Рассмотрев данные примеры, можно сделать вывод, что, овладев техникой применения метода данных множителей можно значительно быстрее двигаться к ответу при решении неравенств, предлагаемых в конкурсных заданиях. Мы рассмотрели задания, предлагаемые на вступительных экзаменах по математике на основных факультетах МГУ.
Метод замены множителей применяется при решении неравенств, содержащих показательные и логарифмические выражения.