Организация и исследование параллельно-последовательных вычислений на кластере мэи при решении класса матричных задач большой р

АКТУАЛЬНОСТЬ РАБОТЫ
Высокопроизводительные вычисления востребованы в задачах
моделирования климата;
генной инженерии;
проектирования интегральных схем;
анализа загрязнения окружающей среды;
создания лекарственных препаратов и многих других.

ЦЕЛЬ РАБОТЫ
Провести исследование эффективности параллельно-последовательных вычислений на кластере МЭИ при решении СЛАУ и матричном умножении.
Основные задачи:
Исследование классических методов решения некоторых матричных задач.
Разработка параллельных модификаций и изучение способов повышения эффективности вычислений за счет организации параллелизма и учета особенностей задач.
Изучение влияния различных типов обменных взаимодействий на характеристики параллельного решения.

ЗАДАЧА РЕШЕНИЯ СЛАУ С ВЕЩЕСТВЕННЫМИ КОЭФФИЦИЕНТАМИ
Прямые методы
Итерационные методы

ИТЕРАЦИОННЫЙ МЕТОД ЯКОБИ

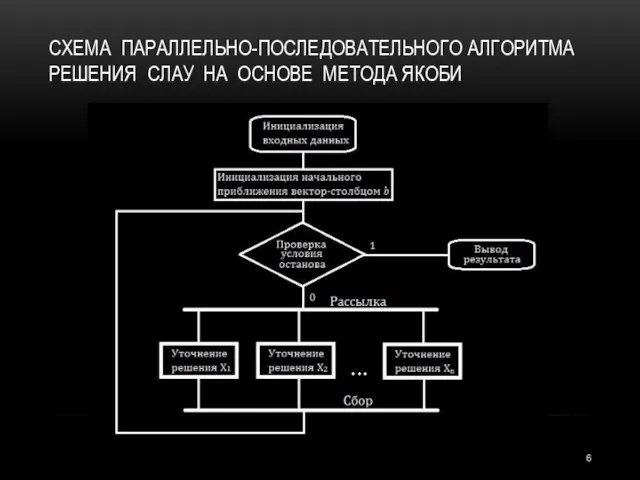
СХЕМА ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОГО АЛГОРИТМА РЕШЕНИЯ СЛАУ НА ОСНОВЕ МЕТОДА ЯКОБИ

ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ НА КЛАСТЕРЕ МЭИ

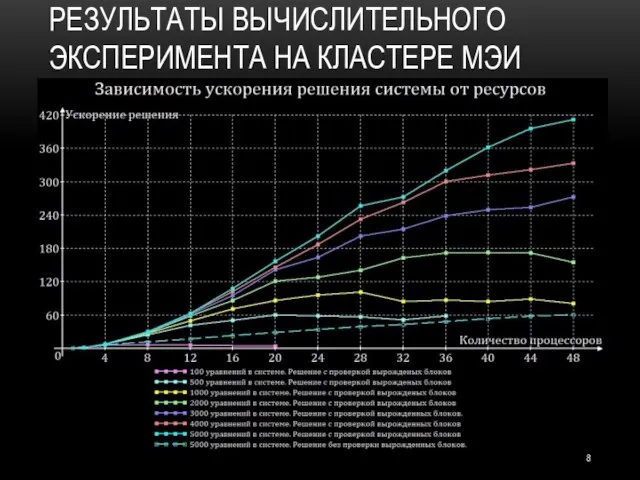
РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА НА КЛАСТЕРЕ МЭИ

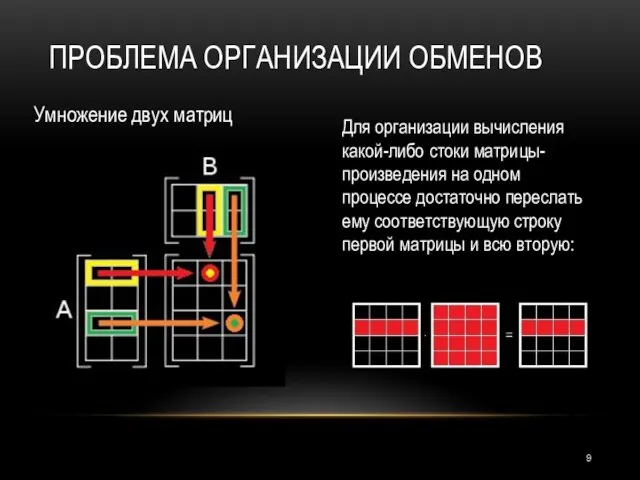
Для организации вычисления какой-либо стоки матрицы-произведения на одном процессе достаточно переслать ему соответствующую строку первой матрицы и всю вторую:
ПРОБЛЕМА ОРГАНИЗАЦИИ ОБМЕНОВ
Умножение двух матриц

ОСОБЕННОСТИ МОДИФИКАЦИИ МАТРИЧНОГО УМНОЖЕНИЯ
В разработанной модификации матрицы разбиваются на
квадратные блоки.

РЕЖИМЫ РАБОТЫ ПРОГРАММЫ МАТРИЧНОГО УМНОЖЕНИЯ
Проверка наличия блоков, полностью состоящих из нулевых элементов
Использование исключительно точечных обменов между вычислительными узлами или точечных и массовых обменных взаимодействий
Выбор размерности блоков (влияние на зернистость распараллеливания)

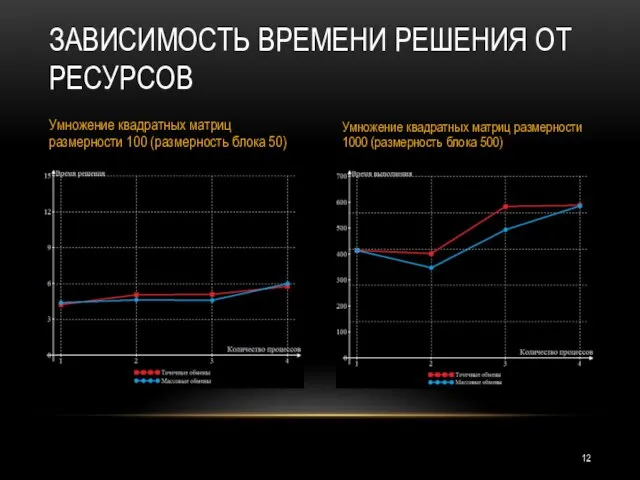
ЗАВИСИМОСТЬ ВРЕМЕНИ РЕШЕНИЯ ОТ РЕСУРСОВ
Умножение квадратных матриц размерности 100 (размерность блока 50)
Умножение квадратных матриц размерности 1000 (размерность блока 500)

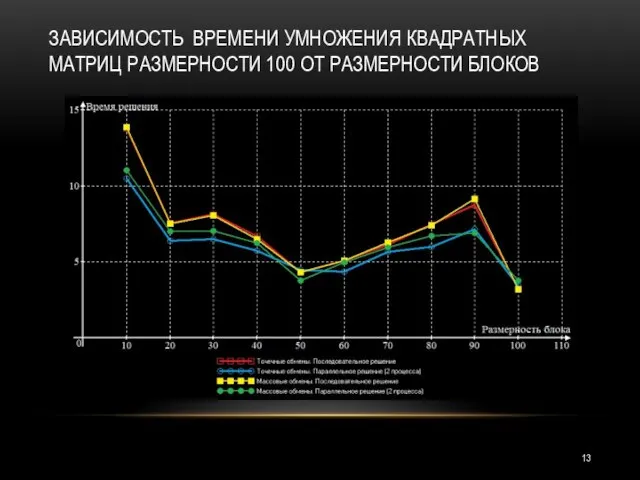
ЗАВИСИМОСТЬ ВРЕМЕНИ УМНОЖЕНИЯ КВАДРАТНЫХ МАТРИЦ РАЗМЕРНОСТИ 100 ОТ РАЗМЕРНОСТИ БЛОКОВ

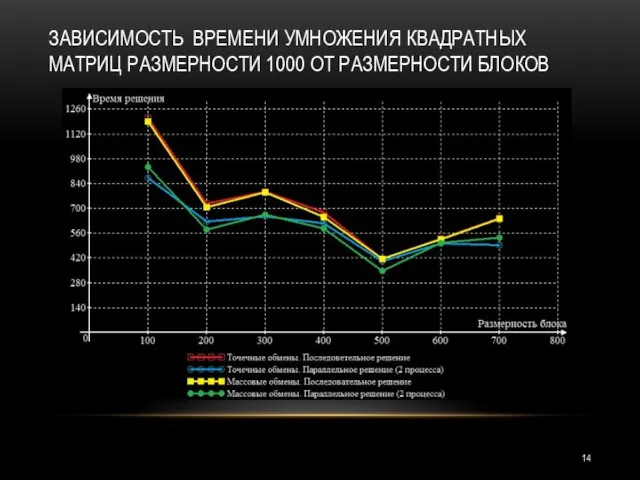
ЗАВИСИМОСТЬ ВРЕМЕНИ УМНОЖЕНИЯ КВАДРАТНЫХ МАТРИЦ РАЗМЕРНОСТИ 1000 ОТ РАЗМЕРНОСТИ БЛОКОВ

ИТОГИ РАБОТЫ
На основе алгоритма матричного умножения и классических методов решения СЛАУ разработаны и реализованы их параллельные модификации
Проведены исследования ускорений реализованных алгоритмов в зависимости от размерности задач, вычислительных ресурсов, видов обменных взаимодействий и учета специфики задач
Получены практические навыки по разработке, отладке и тестированию параллельных программ и исследования их эффективности. Освоена специфика работы с кластером МЭИ
Основные результаты работы представлены на двух конференциях и опубликованы соответствующие доклады
XVIII международная научно-техническая конференция студентов и аспирантов «Радиоэлектроника, электротехника и энергетика»
VI Всероссийская студенческая научно-техническая конференция «Прикладная информатика и математическое моделирование»