02-04

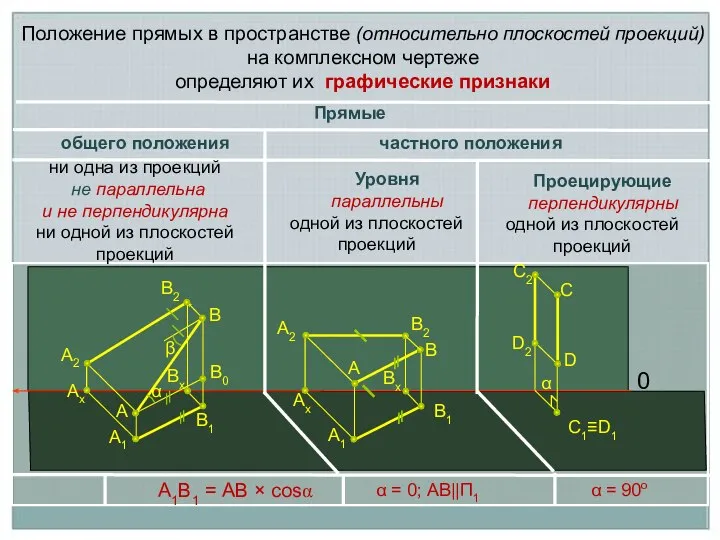
α
β
A1
B1
A
A2
Ax
B
B2
α = 0; АВ||П1
A1
B1
A
A2
Ax
C
C2
0
B
B2
D
D2
C1≡D1
α = 90o
А1В1 = АВ × cosα
Положение прямых в пространстве (относительно плоскостей проекций)
на комплексном чертеже
определяют их графические признаки
Прямые
общего положения частного положения
Уровня
параллельны одной из плоскостей проекций
Проецирующие
перпендикулярны одной из плоскостей проекций
Вx
Вx
B0
ни одна из проекций
не параллельна
и не перпендикулярна
ни одной из плоскостей
проекций
α

Линии уровня

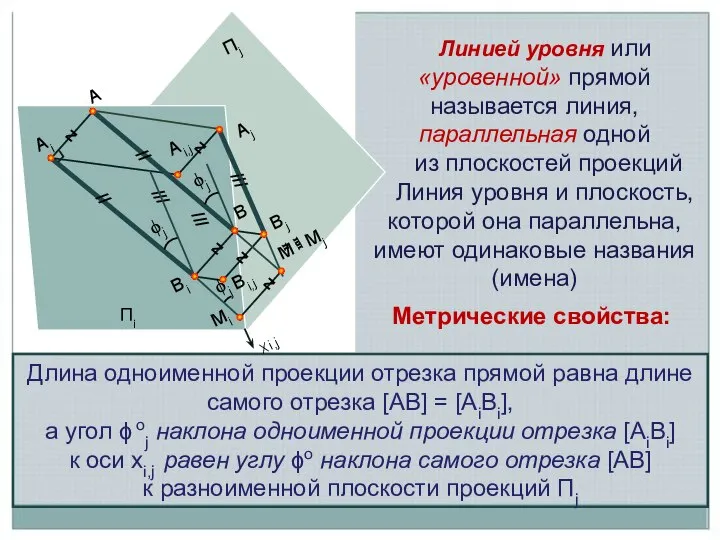
Линией уровня или «уровенной» прямой называется линия, параллельная одной
из плоскостей проекций
Линия уровня и плоскость, которой она параллельна, имеют одинаковые названия (имена)
Метрические свойства:
Длина одноименной проекции отрезка прямой равна длине самого отрезка [АВ] = [АiВi],
а угол ϕ оj наклона одноименной проекции отрезка [АiВi]
к оси хi,j равен углу ϕо наклона самого отрезка [АВ]
к разноименной плоскости проекций Πj
Пi
Пj
Xi,j
Aj
Ai
B
Bi
A
Bj
//
///
z
z
ϕj
М Мj
ппп
//
///
z
z
z
ϕj
///
ϕj
Мi
Bi,j
Ai,j

h2
h3
h1=нв[h]
П1
П2
Х1,2
Zh
Zh
Zh
Zh
П3
Z(х2,3)
Y(х1,3)
Y(х1,3)
h – горизонталь
ϕ3
ϕ2
h2
h1
h3
h
z(х2,3)
y(х1,3)
x1,2

f1
f2=нв[f]
Х1,2
yf
П3
Z(х2,3)
Y(х1,3)
f – фронталь
yf
yf
yf
f3
ϕ1
ϕ3
Y(х1,3)
П2
П1
f3
f1
f2
f
x1,2
y(х1,3)
z(х2,3)
П3
П2
П1
//
//

р – профильная прямая
р1
р3=нв[р]
Х1,2
П3
Z(Х2,3)
Y(Х1,3)
yf
yр
р3
ϕ1
ϕ3
Y(Х1,3)
р2
хр
хр
П2
П1
хр
хр
yр
р2
р3
р1
р
z(х2,3)
y(х1,3)
x1,2

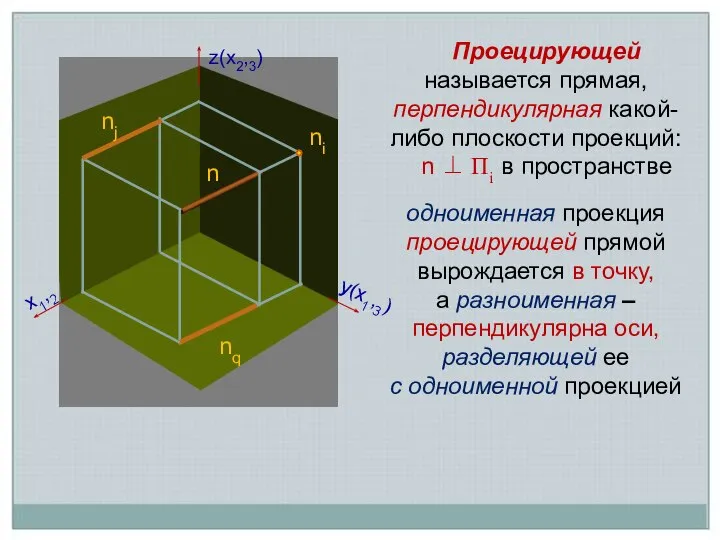
Проецирующей называется прямая, перпендикулярная какой-либо плоскости проекций:
n ⊥ Пi в пространстве
n
nj
ni
nq
одноименная проекция проецирующей прямой вырождается в точку,
а разноименная – перпендикулярна оси, разделяющей ее
с одноименной проекцией
x1,2
y(х1,3)
z(х2,3)