Содержание
- 2. Урок алгебры и начал анализа по теме «Применение интегрального исчисления к решению прикладных задач в экономике»
- 3. Здравствуйте!
- 4. Cмысл - там, где змеи интеграла Меж цифр и букв, меж d и f. В.Я. Брюсов
- 5. F(x) Свойства первообразной S криволинейной трапеции Интеграл Таблица первообразных Правила вычисления первообразных
- 6. 1. Как называется функция F(x) для f(x)? 2. Что является графиком функции у=кх+b? 3. Самая низкая
- 7. Верно ли что: а) б)
- 8. Верны ли равенства: а) б) в) г) д) ?
- 9. Найти первообразные для функций: а) f(x) =10х б) f(x) = х² в) f(x) =-sin(2x) г) f(x)
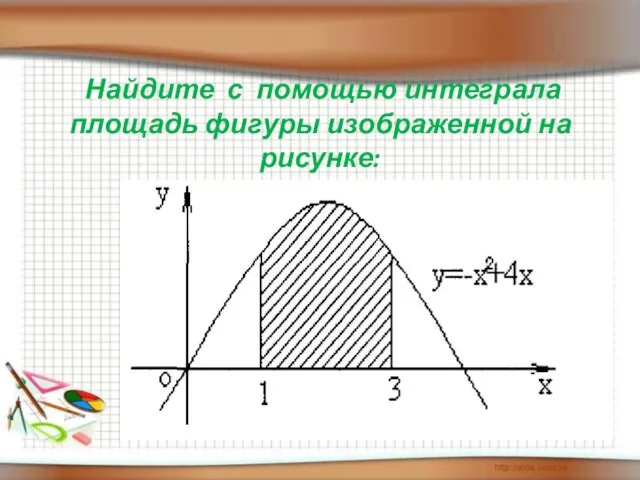
- 10. Найдите с помощью интеграла площадь фигуры изображенной на рисунке:
- 11. Вычисление площади плоской фигуры в прямоугольных координатах Вычисление объема тела вращения Вычисление площади поверхности тела вращения
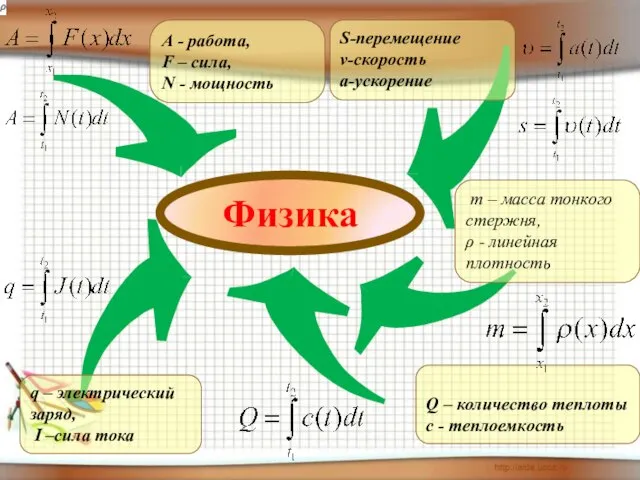
- 12. S-перемещение v-скорость а-ускорение m – масса тонкого стержня, ρ - линейная плотность q – электрический заряд,
- 13. «Применение интегрального исчисления к решению прикладных задач в экономике»
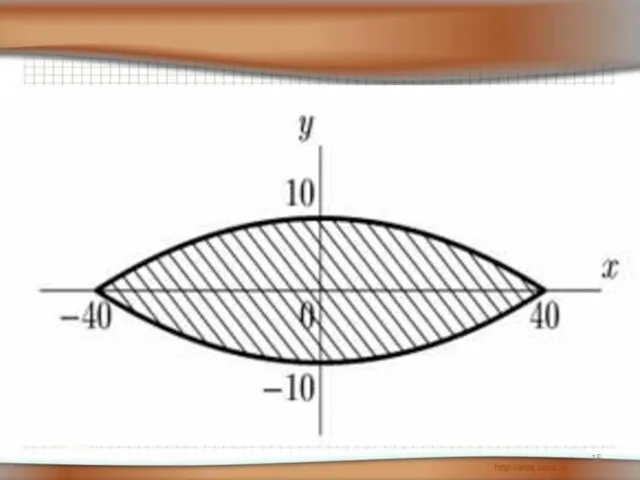
- 14. ► Прогнозирование материальных затрат Задача. Палуба корабля напоминает две пересекающиеся параболы. Сколько необходимо краски для ее
- 16. ► Определения объема выпуска продукции Задача. Определить объем продукции, произведенной рабочим за третий час рабочего дня,
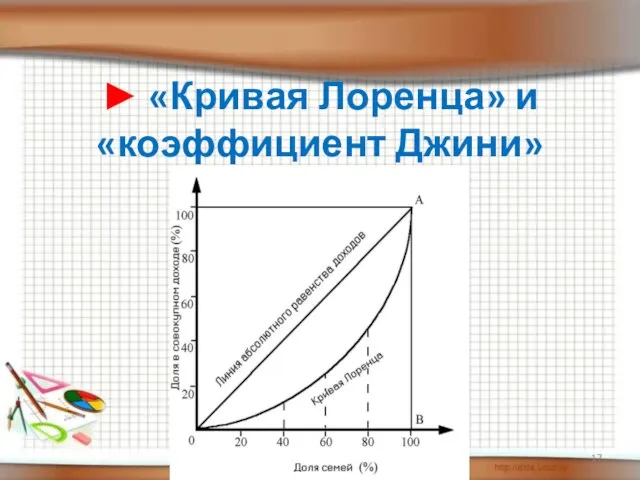
- 17. ► «Кривая Лоренца» и «коэффициент Джини»
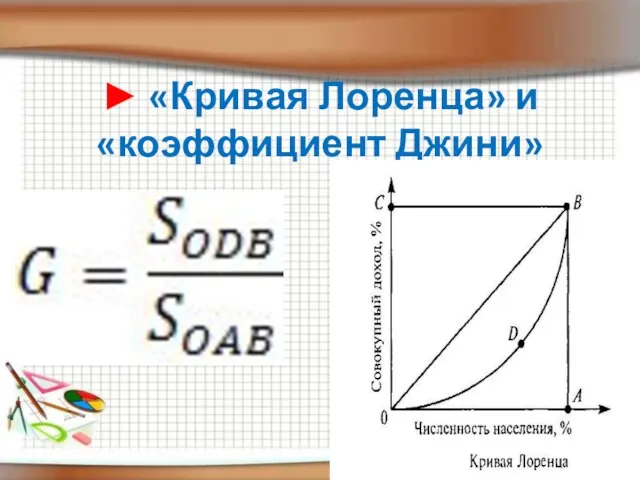
- 18. ► «Кривая Лоренца» и «коэффициент Джини»
- 19. ► «Кривая Лоренца» и «коэффициент Джини»
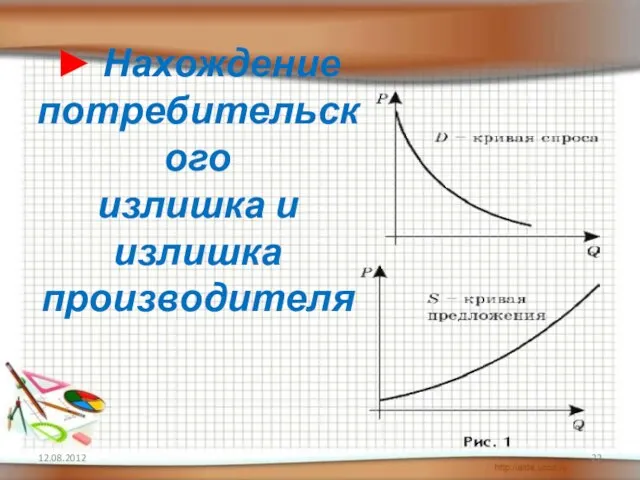
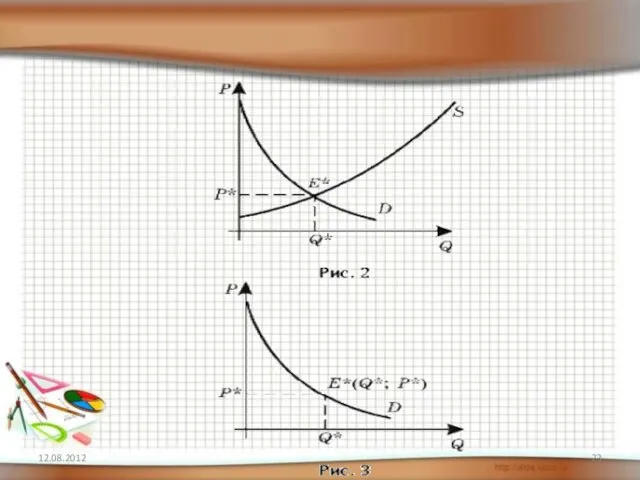
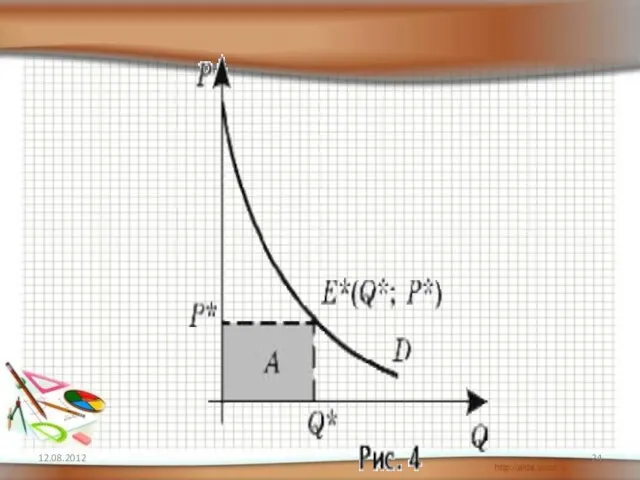
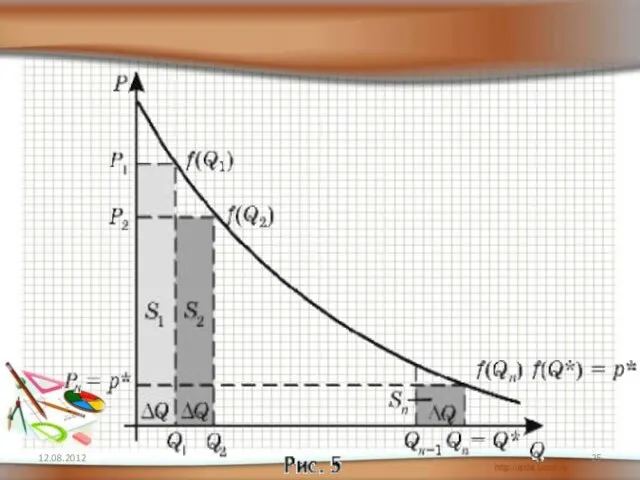
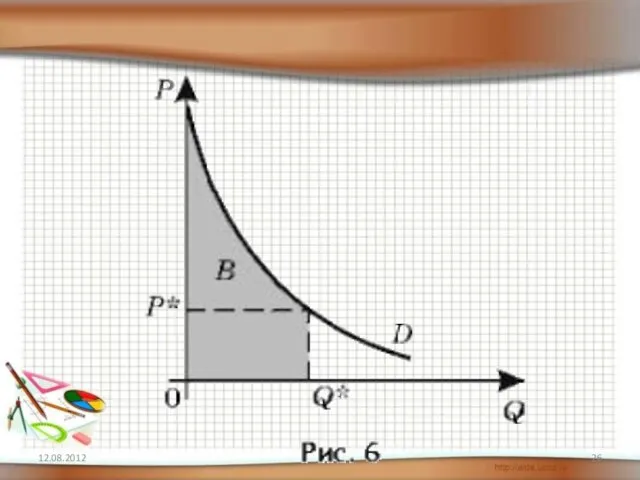
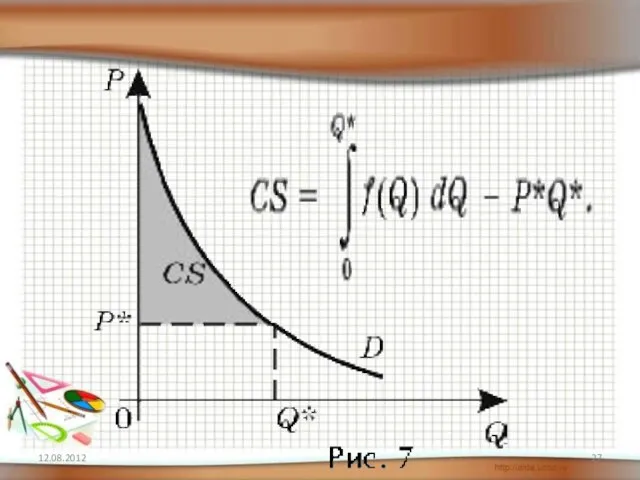
- 22. ► Нахождение потребительского излишка и излишка производителя 12.08.2012
- 23. 12.08.2012
- 24. 12.08.2012
- 25. 12.08.2012
- 26. 12.08.2012
- 27. 12.08.2012
- 28. ► Нахождение потребительского излишка Задача. Известно, что спрос на некоторый товар описывается функцией а предложение данного
- 29. ► Нахождение потребительского излишка Задача. Известно, что спрос на некоторый товар задается функцией предложение – функцией
- 30. 12.08.2012
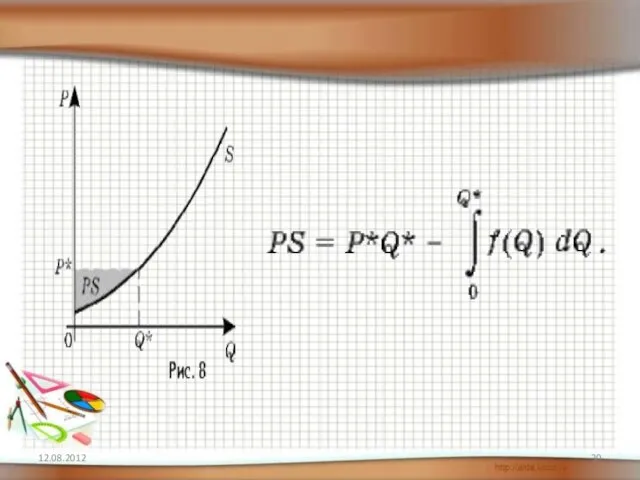
- 31. ► Нахождение излишка производителя Задача. Известно, что кривая предложения некоторого товара имеет вид p = 4q3
- 32. ► Нахождение дисконтированной стоимости денежного потока 12.08.2012 . П =
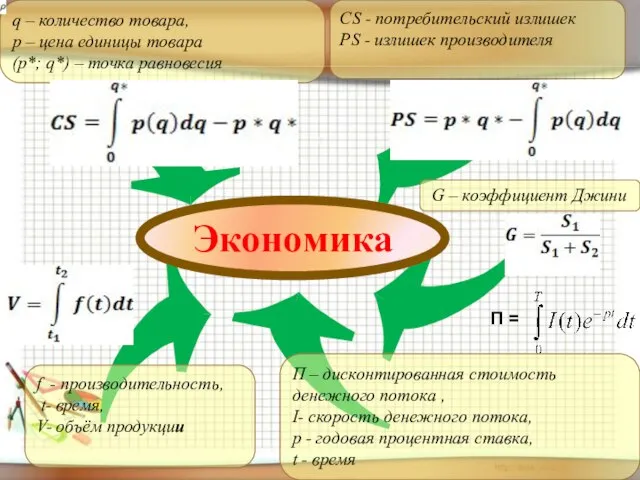
- 33. СS - потребительский излишек PS - излишек производителя G – коэффициент Джини f - производительность, t-
- 34. ► Домашнее задание Задача 1. Определить запас товаров в магазине, образуемый за три дня, если поступление
- 35. Урок окончен. За что ты можешь себя похвалить? Что тебе удалось на уроке? Над чем ещё
- 37. Скачать презентацию


















 Фестиваль успехаВыступление 23. 04. 2012
Фестиваль успехаВыступление 23. 04. 2012 Состояние и показатели тренированности спортсмена
Состояние и показатели тренированности спортсмена Состав предметов
Состав предметов Сделаем нашу планету чистой!
Сделаем нашу планету чистой! Стресс – разрушитель нашего организма
Стресс – разрушитель нашего организма Психологическая подготовка боксеров-юношей
Психологическая подготовка боксеров-юношей День Хлеба! 4 класс
День Хлеба! 4 класс Исследовательское обучение учащихся во внеурочной деятельности по ФГОС - презентация для начальной школы_
Исследовательское обучение учащихся во внеурочной деятельности по ФГОС - презентация для начальной школы_ Город-герой Киев
Город-герой Киев ОРГАНИЗАЦИЯ СЛУЖБЫ ЭКСТРАКОРПОРАЛЬНОЙ КОРРЕКЦИИ ГОМЕОСТАЗА ВВ МНОГОПРОФИЛЬНОМ СТАЦИОНАРЕ
ОРГАНИЗАЦИЯ СЛУЖБЫ ЭКСТРАКОРПОРАЛЬНОЙ КОРРЕКЦИИ ГОМЕОСТАЗА ВВ МНОГОПРОФИЛЬНОМ СТАЦИОНАРЕ The Police in Britain
The Police in Britain Викторина по финансовой грамотности
Викторина по финансовой грамотности Публичный отчёт о работе ГОУ СОШ «Школа здоровья» № 568 за 2009 -2010 учебный год
Публичный отчёт о работе ГОУ СОШ «Школа здоровья» № 568 за 2009 -2010 учебный год Презентация на тему ПРОИСХОЖДЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ ПЕРВЫЕ РАЗМЫШЛЕНИЯ И НАУЧНОЕ ОБЪЯСНЕНИЕ
Презентация на тему ПРОИСХОЖДЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ ПЕРВЫЕ РАЗМЫШЛЕНИЯ И НАУЧНОЕ ОБЪЯСНЕНИЕ  Методические проблемы проектирования образовательной среды ВУЗа
Методические проблемы проектирования образовательной среды ВУЗа Подзаконные акты, действующие в сфере туризма
Подзаконные акты, действующие в сфере туризма Информационное обеспечение арбитражных судов и участников судебного процесса
Информационное обеспечение арбитражных судов и участников судебного процесса Народный промысел – Гжель
Народный промысел – Гжель Международный опыт реформы организации управления общественными финансами
Международный опыт реформы организации управления общественными финансами ШКОЛЬНОЕ МЕТОДИЧЕСКОЕ ОБЪЕДИНЕНИЕ УЧИТЕЛЕЙ ТЕХНОЛОГИИ И ЧЕРЧЕНИЯ
ШКОЛЬНОЕ МЕТОДИЧЕСКОЕ ОБЪЕДИНЕНИЕ УЧИТЕЛЕЙ ТЕХНОЛОГИИ И ЧЕРЧЕНИЯ Внутриорганизационные конфликты
Внутриорганизационные конфликты Период развития италийских племён
Период развития италийских племён  Система работы с текстом на уроках русского языка как средство формирования коммуникативной компетентности
Система работы с текстом на уроках русского языка как средство формирования коммуникативной компетентности День Святого Миколая
День Святого Миколая Проект “На одной волне”
Проект “На одной волне” Урок по истории Древнего мира в 5 классе.
Урок по истории Древнего мира в 5 классе. Литургия Преждеосвящённых Даров
Литургия Преждеосвящённых Даров Паломничества и святыни (4 класс)
Паломничества и святыни (4 класс)