1D проводимость невзаимодействующих электронов

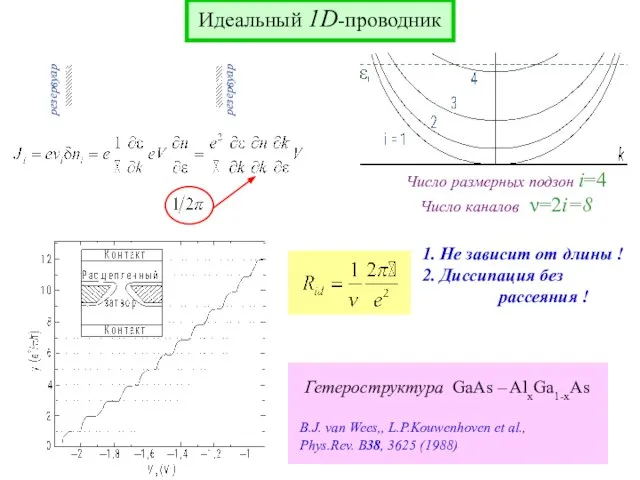
Идеальный 1D-проводник
резервуар
резервуар
Число размерных подзон i=4 Число каналов ν=2i=8
B.J. van Wees,, L.P.Kouwenhoven et al.,
Phys.Rev. B38, 3625 (1988)
Гетероструктура GaAs – AlxGa1-xAs
1. Не зависит от длины !
2. Диссипация без
рассеяния !

Формула Ландауэра

Двухбарьерный дефект
Решение:
Если два барьера одинаковы (r1= r2= r, R 1= R 2= R и т.д.) , то формула существенно упрощается
зависит
от расстояния l
и
от импульса k

Двухбарьерный дефект (продолжение)
можно сравнить с ...
…и с результатом усреднения
…классич.
выражением
Формулу
Такое усреднение не всегда корректно, но в дальнейшем мы им воспользуемся

1D − локализация
Цепочка из N случайно расположенных слабых рассеивателей
в проволоке длиной L = l N (l – среднее расстояние между рассеивателями)
Вычисляем сопротивление
по реккурентной формуле (по индукции)
Мы воспользовались формулой, полученной после усреднения
R << 1,
T ~ 1
R
T
R
Пока N мало, R N и RN растут линейно: RN ~ N.
Это – закон Ома .

При больших N и
при
1D − локализация (продолжение)
R N R N-1 1
R
Длина пробега l = l /R
ОПРЕДЕЛЕНИЕ
Другая форма записи
ξ = l / |ln T | l /R = l
В одноканальном 1D–проводнике ξ = l !!

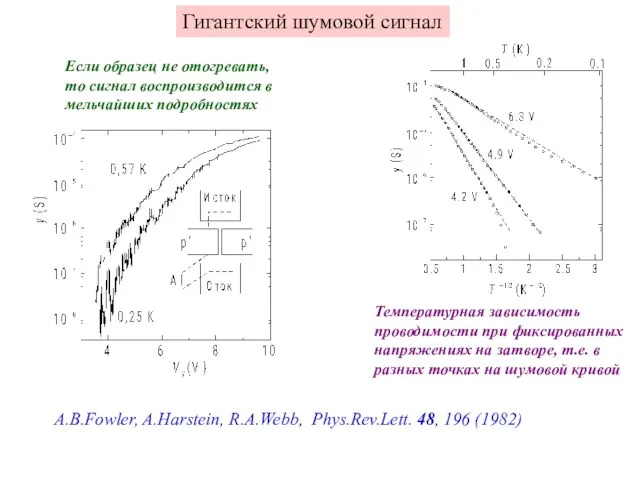
Гигантский шумовой сигнал
A.B.Fowler, A.Harstein, R.A.Webb, Phys.Rev.Lett. 48, 196 (1982)
Если образец не отогревать, то сигнал воспроизводится в мельчайших подробностях
Температурная зависимость проводимости при фиксированных напряжениях на затворе, т.е. в разных точках на шумовой кривой

Роль корреляций
Рассеиватель из двух одинаковых барьеров на расстоянии (r1= r2= r и т. д.)
абсолютно прозрачен для волны с волновым вектором k = k0 = − arg r /l . Если заменить случайно расположенные барьеры на сдвоенные, то электрон с энергией εo = h 2ko2/2m окажется делокализованным.
Димерная модель. Одномерная цепочка периодически расположенных пар ям двух сортов (Еa и Еb )
Если |Ea− Eb| < 2J, то делокализованным оказывается состояние
J − интеграл перекрытия

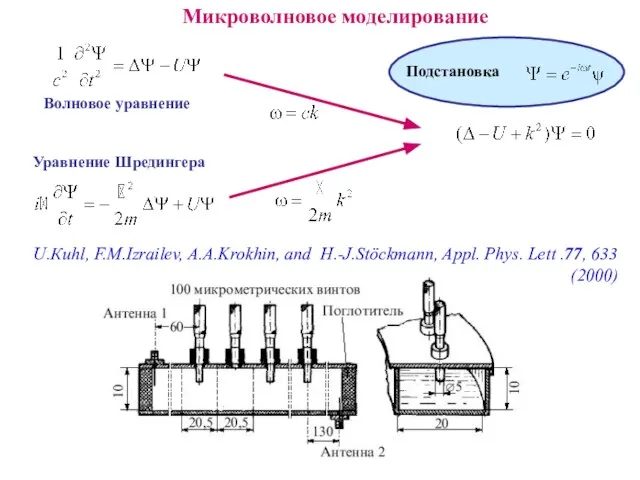
Микроволновое моделирование
Уравнение Шредингера
Волновое уравнение
Подстановка
U.Кuhl, F.M.Izrailev, A.A.Krokhin, and H.-J.Stöckmann, Appl. Phys. Lett .77, 633 (2000)

Zm+n − случайные числа из интервала [ −1, +1 ]
Функция ϕ(μ) определяет спектр пропускания
Коэффициенты βm обеспечивают корреляции между величинами un
Алгоритм построения модельного потенциала, обеспечивающего появление окон прозрачности