Содержание
- 2. Математики видят ее в: гармонии чисел и форм, геометрической выразительности, стройности математических формул, решении задач различными
- 3. Но красота математики выражается не только в красоте форм ,наглядной выразительности математических объектов, восприятие которых сопряжено
- 4. Можно ли насладиться решением уравнения sinx-cosx=1? Да, если стать его исследователем!
- 5. Универсальные методы решения уравнения sin x – cos x=1 Мы уже говорили о богатстве приложений универсальных
- 6. Мы не просто в правой части уравнения получили ноль,мы выделили выражение 1 + cos x …
- 7. Ну, конечно,вы догадались ! Необходимо перейти к половинному аргументу, применив формулу повышения степени и формулу двойного
- 8. Разложение левой части уравнения на множители sinx-cosx=1
- 9. Произведение равно нулю, если хотя бы один из множителей равен нулю, а остальные при этом не
- 10. Делим обе его части на что противоречит тождеству Получим Ответ:
- 11. Приведение уравнения к однородному относительно синуса и косинуса sinx-cosx=1 Разложим левую часть по формулам двойного аргумента,
- 12. Тригонометрия удивительна тем ,что она даёт собственные оригинальные способы преобразования разности (или суммы) тригонометрических функций в
- 13. Преобразование разности ( или суммы) тригонометрических функций в произведение. sinx-cosx=1 Запишем уравнение в виде: Применяя формулу
- 14. 4-й способ Приведение к квадратному уравнению относительно одной из функций Так как Возведем обе части полученного
- 15. В процессе решения обе части уравнения возводились в квадрат, что могло привести к появлению посторонних решений,
- 16. Первое и второе решения совпадают с ранее полученными, поэтому не являются посторонними. Проверим Левая часть: Правая
- 17. 5-й способ Выражение всех функций через tgx (универсальная подстановка) по формулам: С учетом приведенных формул уравнение
- 18. Умножим обе части уравнения на ОДЗ первоначального уравнения – все множество R.
- 19. При переходе к из рассмотрения выпали значения, при которых не имеет смысла, т.е. Следует проверить, не
- 20. На ряду с универсальными методами решения уравнений, есть и специфические. Наиболее ярким из них является метод
- 21. 6-й способ Введение вспомогательного угла (числа) sinx-cosx=1 В левой части вынесем за скобку ( корень квадратный
- 22. 7-способ Возведение обеих частей уравнения в квадрат sinx-cosx=1
- 23. Полученное решение эквивалентно объединению четырех решений: Проверка показывает, что первое и четвертое решения – посторонние. Ответ:
- 25. Скачать презентацию



















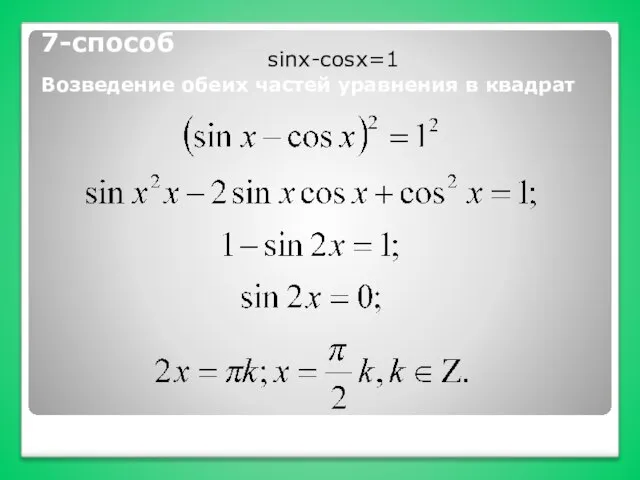

 Инвестиции в номерной фонд апарт-отеля
Инвестиции в номерной фонд апарт-отеля Викторина по истории изобразительного искусства Древняя Русь
Викторина по истории изобразительного искусства Древняя Русь Оценка пространственных внешних эффектов для России
Оценка пространственных внешних эффектов для России В.Терешкова – первая женщина-космонавт
В.Терешкова – первая женщина-космонавт Я – ребёнок, я - человек!
Я – ребёнок, я - человек! Зоя Космодемьянская
Зоя Космодемьянская История психологии
История психологии Грабли Как мы наступали на грабли…
Грабли Как мы наступали на грабли… Интеллектуада ВУЗОВ Санкт-Петербурга
Интеллектуада ВУЗОВ Санкт-Петербурга Заводські дефекти лакофарбного покриття(ЛФП) тепловозів серії ТЕ33АС
Заводські дефекти лакофарбного покриття(ЛФП) тепловозів серії ТЕ33АС Внешнеполитические интересы
Внешнеполитические интересы Вазоренальная артериальная гипертензия
Вазоренальная артериальная гипертензия И
И Новогодняя вечерника в Хокку
Новогодняя вечерника в Хокку Презентация на тему Что такое функция (7 класс)
Презентация на тему Что такое функция (7 класс) У каждого из нас в жизни случаются трудности
У каждого из нас в жизни случаются трудности Государство и налоги
Государство и налоги Химия - страна чудес
Химия - страна чудес х
х Lifestyle of students in St. Petersburg
Lifestyle of students in St. Petersburg Информация по реализации 83-ФЗ
Информация по реализации 83-ФЗ Олимпийская гордость Санкт-Петербурга. Лондон 2012
Олимпийская гордость Санкт-Петербурга. Лондон 2012 Преобразование рациональных выражений.
Преобразование рациональных выражений. ФИРМА RESPECT Представляет проект: «Деловой школьник!»
ФИРМА RESPECT Представляет проект: «Деловой школьник!» АО Транснефть-Сибирь. Оптимизация передачи документов через КИС ЭХД
АО Транснефть-Сибирь. Оптимизация передачи документов через КИС ЭХД Административно-территориальное деление РФ (1)
Административно-территориальное деление РФ (1) Периметр Площадь
Периметр Площадь Банковский депозит
Банковский депозит