Содержание
- 2. Логика упорядоченная система мышления, которая создает взаимосвязи между заданными условиями и позволяет делать умозаключения, основываясь на
- 3. Аристотель Древнегреческий философ Основоположник логики Исследовал различные формы рассуждений , ввел понятие силлогизма 384 — 322
- 4. Рене Декарт 1596 − 1650 Французский философ, математик, механик, физик и физиолог Рекомендовал в логике использовать
- 5. Готфрид Вильгельм Лейбниц 1646 − 1716 Немецкий философ, логик, математик, механик, физик, юрист, историк, дипломат, языковед
- 6. Джордж Буль 1815 − 1864 Английский математик и логик Основоположник математической логики «Математический анализ логики» 1847
- 7. Алгебра логики раздел математической логики, в котором изучаются логические операции над высказываниями Алгебра логики = Булева
- 8. Высказывание Предложение, относительно которого имеет смысл утверждать, истинно оно или ложно Истинностные значения: - Ложь или
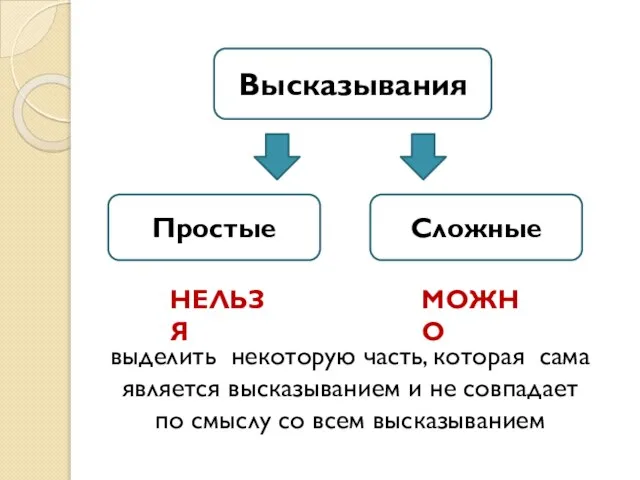
- 9. Высказывания Простые Сложные выделить некоторую часть, которая сама является высказыванием и не совпадает по смыслу со
- 10. Пример Простое высказывание «Ивдель − это город» Сложное высказывание «Ивдель − это красивый и культурный город»
- 11. Обозначения Большие буквы латинского алфавита А – высказывание А = 1 – высказывание истинно А =
- 12. Высказывательные переменные Всякая большая буква латинского алфавита как некоторое переменное высказывание, которое может принимать значения 0
- 13. Логические связки Инверсия (отрицание) Конъюнкция (и) Дизъюнкция (или) Импликация (следование) Эквиваленция
- 14. Инверсия (отрицание) Нет; не; неверно, что… ¬, ′ ,
- 15. Пример А = «Ивдель − культурный город!» Инверсия ¬ А = «Неверно, что Ивдель − культурный
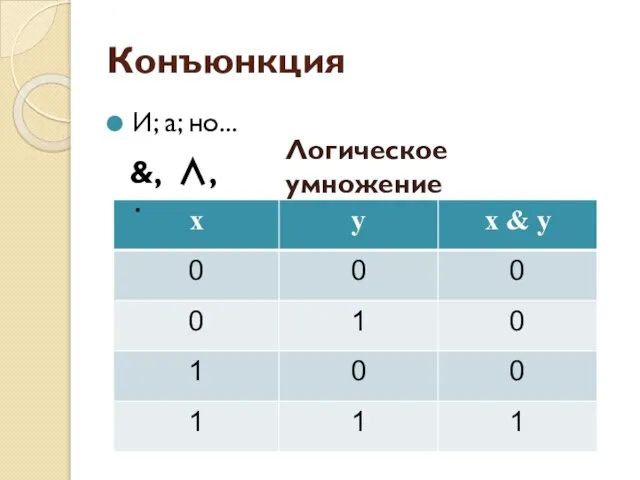
- 16. Конъюнкция И; а; но... &, ∧, ⋅ Логическое умножение
- 17. Пример А = «В Ивделе светит солнце» В = «В Ивделе идёт дождь» Конъюнкция А &
- 18. Задания Известно, что высказывание А&В истинно. Что можно сказать об истинности высказываний А и В? Известно,
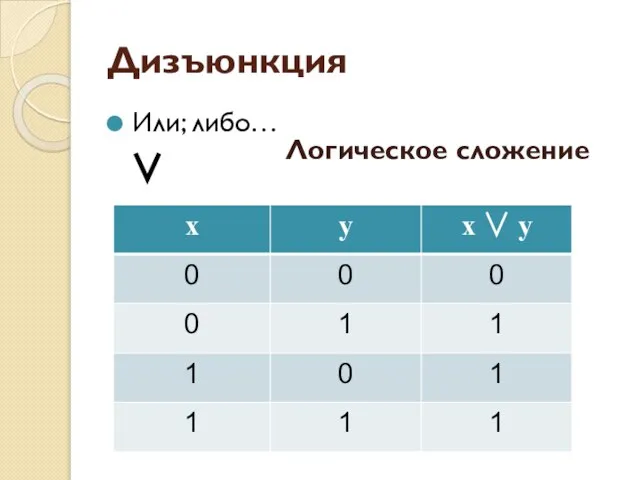
- 19. Дизъюнкция Или; либо… ∨ Логическое сложение
- 20. Пример А = «В Ивделе светит солнце» В = «В Ивделе идёт дождь» Дизъюнкция А ∨
- 21. Задания Известно, что высказывание А∨В истинно. Что можно сказать об истинности высказывания А ∧В? Известно, что
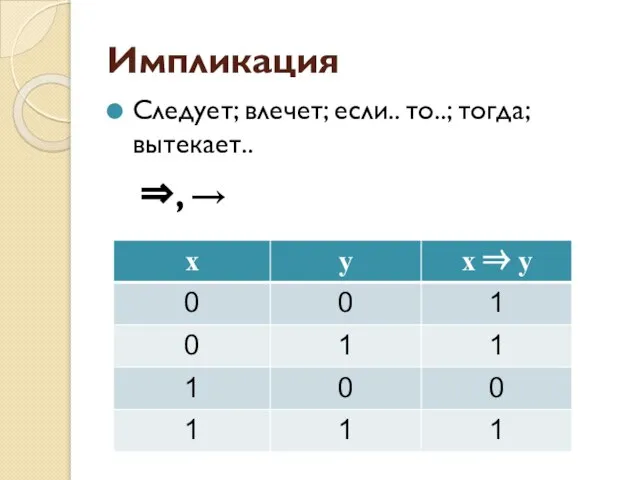
- 22. Импликация Следует; влечет; если.. то..; тогда; вытекает.. ⇒, →
- 23. Пример А = «В Ивделе идёт дождь» В = «В Ивделе мокрые улицы» Импликация А ⇒
- 24. Задания Известно, что высказывание А⇒В истинно. Что можно сказать об истинности высказываний А и В? Известно,
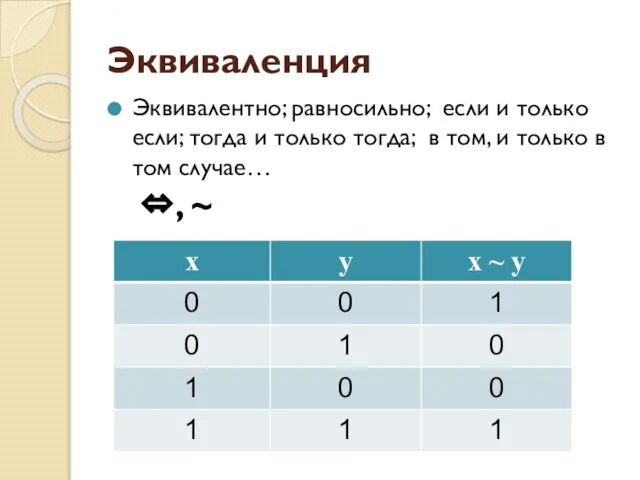
- 25. Эквиваленция Эквивалентно; равносильно; если и только если; тогда и только тогда; в том, и только в
- 26. Пример А = «В Ивделе идёт дождь» В = «В Ивделе мокрые улицы» Эквиваленция А ⇔
- 27. Задание Известно, что высказывание А~В истинно. Что можно сказать об истинности высказываний ¬А ~В и А→В?
- 28. Формулы 1) большие буквы латинского алфавита, снабжённые, быть может, штрихами или индексами и обозначающие высказывания или
- 29. Формулы 2) Если a и b – формулы, то выражения ¬a, a & b, a ∨
- 30. Приоритет логических связок Инверсия Конъюнкция Дизъюнкция Импликация и эквиваленция
- 31. Логическая возможность формулы Формула a(A1, A2, …, An) Всякий набор конкретных значений истинности для букв A1,
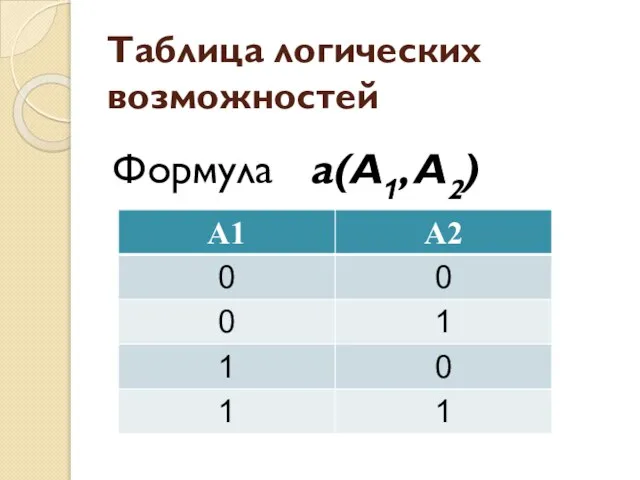
- 32. Таблица логических возможностей Таблица , содержащая перечень всевозможных логических возможностей формулы а
- 33. Таблица логических возможностей Формула a(A1, A2)
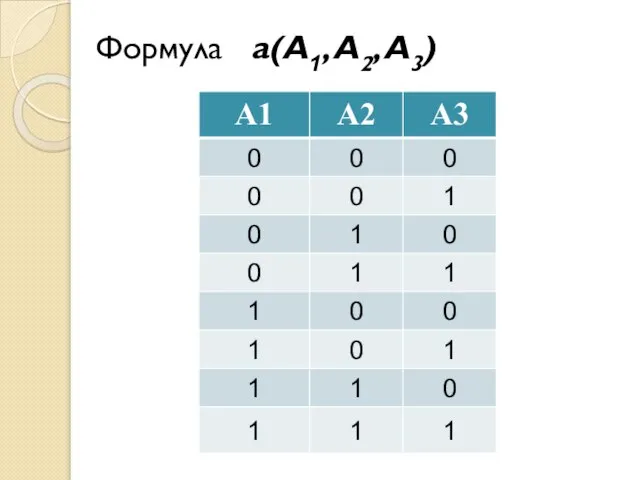
- 34. Формула a(A1, A2, A3)
- 35. Пусть a и b – две формулы, а A1, A2, …, An – все высказывательные переменные
- 36. Пример Найти общие логические возможности формул
- 37. Таблица истинности Таблица ,в которой приведён перечень всевозможных логических возможностей формулы а вместе с указанием её
- 38. Формулы a и b называются равносильными, если во всякой общей логической возможности они принимают одинаковые значения
- 39. Формула называется тождественно истинной (тавтологией) , если во всех логических возможностях она принимает одно и то
- 40. Формула называется тождественно ложной (противоречием) , если во всех логических возможностях она принимает одно и то
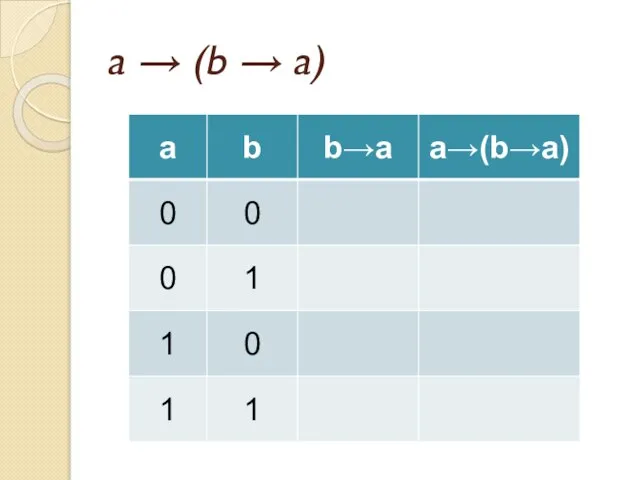
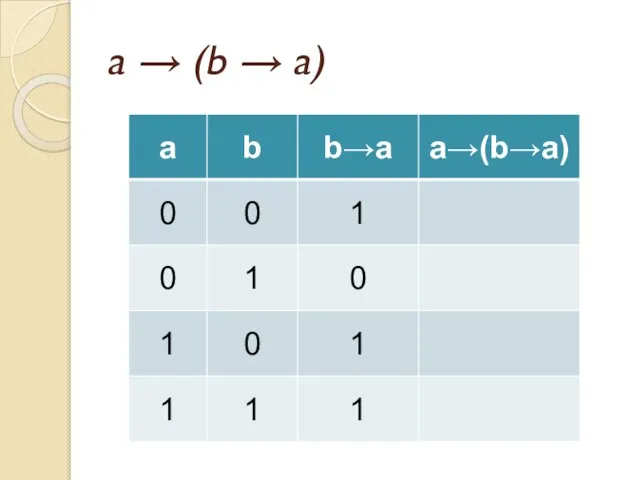
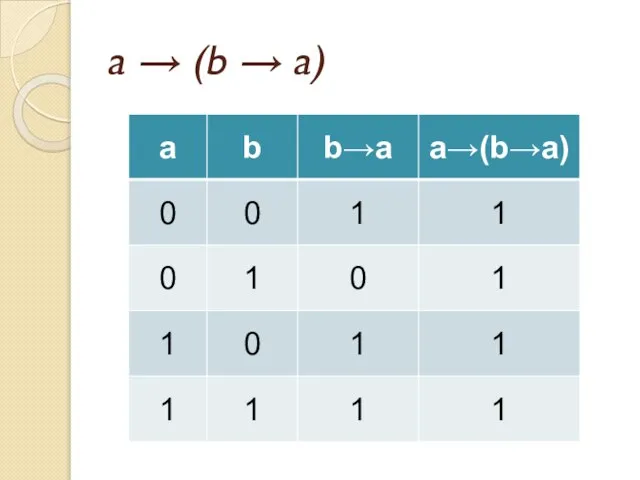
- 41. Задача Докажите тождественную истинность формулы a → (b → a)
- 42. a → (b → a)
- 43. a → (b → a)
- 44. a → (b → a)
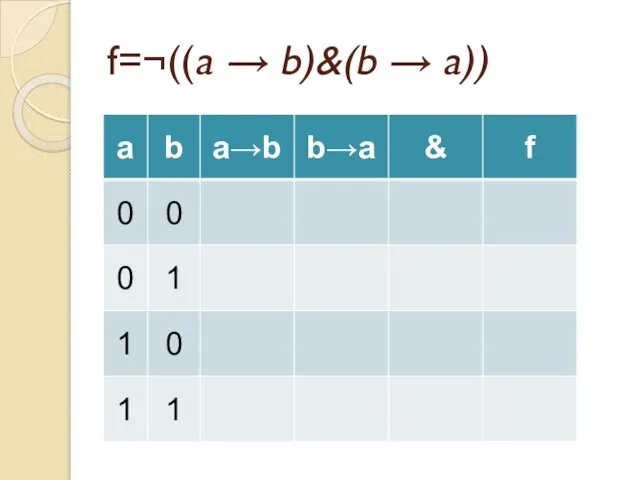
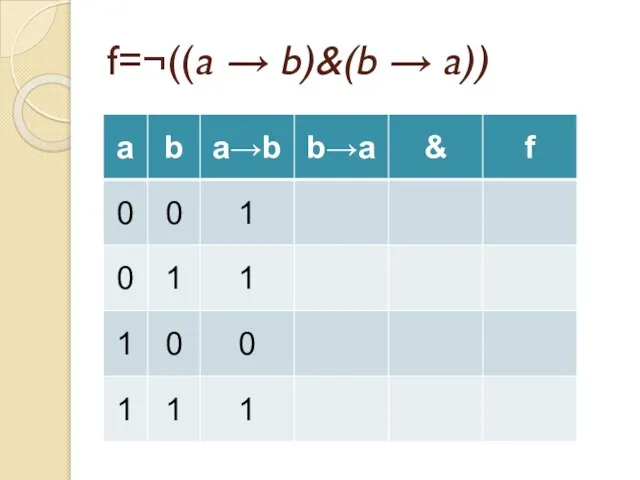
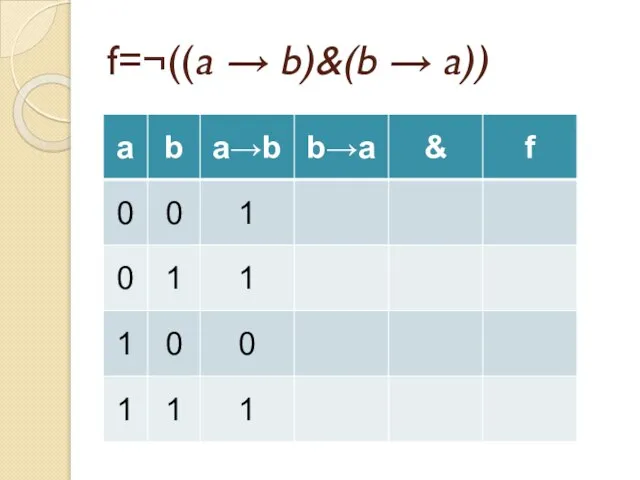
- 45. Задача Докажите тождественную истинность формулы a → (b → a) Постройте таблицу истинности для формулы ¬((a
- 46. f=¬((a → b)&(b → a))
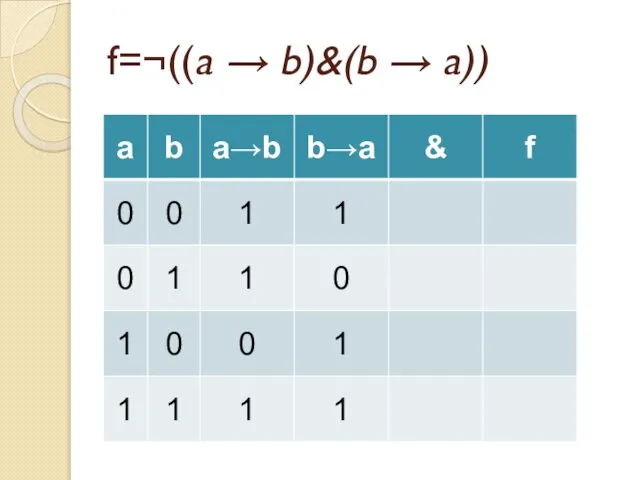
- 47. f=¬((a → b)&(b → a))
- 48. f=¬((a → b)&(b → a))
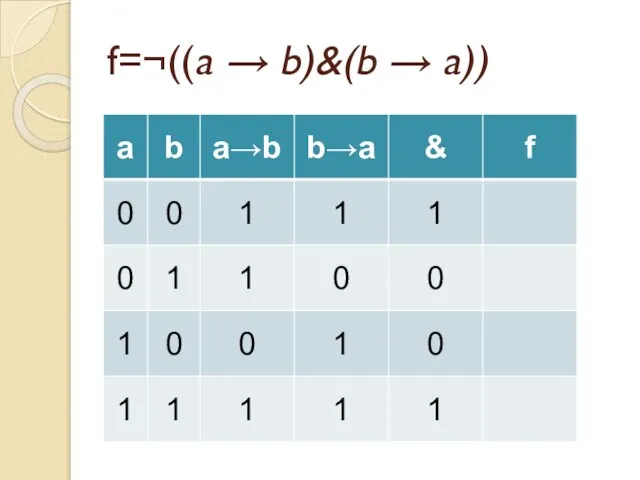
- 49. f=¬((a → b)&(b → a))
- 50. f=¬((a → b)&(b → a))
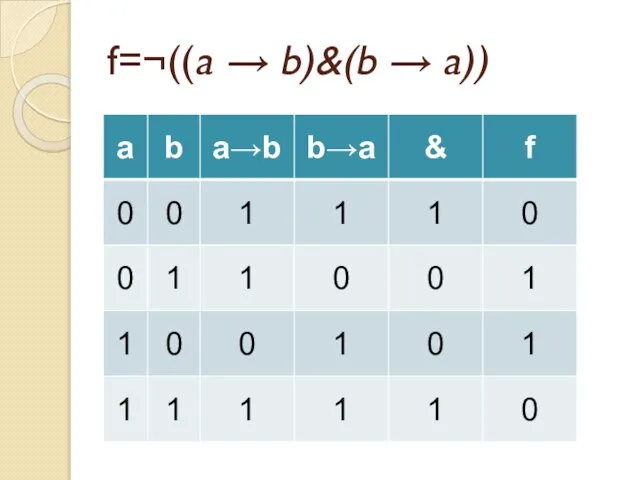
- 51. f=¬((a → b)&(b → a))
- 52. ЗАКОНЫ ЛОГИКИ
- 53. 1. Тождества a & a ≡ a a ∨ a ≡ a
- 54. 2. Переместительный a & b ≡ b & a a ∨ b ≡ b ∨ a
- 55. 3. Сочетательный a & (b & с) ≡ (a & b) & с a ∨ (b
- 56. 4. Распределительный a& (b∨с) ≡ (a&b) ∨ (a&с) a ∨ (b & с) ≡ (a ∨
- 57. 5. Закон двойного отрицания ¬(¬a) ≡ a
- 58. 6. Законы поглощения a & (a ∨ b) ≡ a a ∨ (a & b) ≡
- 59. Огастес де Морган Шотландский математик и логик Первый президент Лондонского математического общества 1847 − элементы логики
- 60. 7. Законы де Моргана ¬(a ∨ b) ≡ ¬a & ¬ b ¬(a & b) ≡
- 61. 8. Закон исключённого третьего ¬a ∨ a ≡ 1
- 62. 9. Закон противоречия ¬a & a ≡ 0
- 63. 10. Свойства тавтологии и противоречия 1 & a ≡ a 1 ∨ a ≡ 1 0
- 64. 11. Закон контрапозиции (контроппозиции) a → b ≡ ¬b → ¬ a
- 65. 12. Правило исключения импликации a → b ≡ ¬ a ∨ b
- 66. 13. Правило исключения эквиваленции a ~ b ≡ (a → b) &(b → a)
- 67. Задача Докажите тождественную истинность формулы c помощью законов логики a → (b → a)
- 69. Задача Упростите формулу ¬((a → b)&(b → a))
- 72. РЕЛЕЙНО-КОНТАКТНЫЕ СХЕМЫ
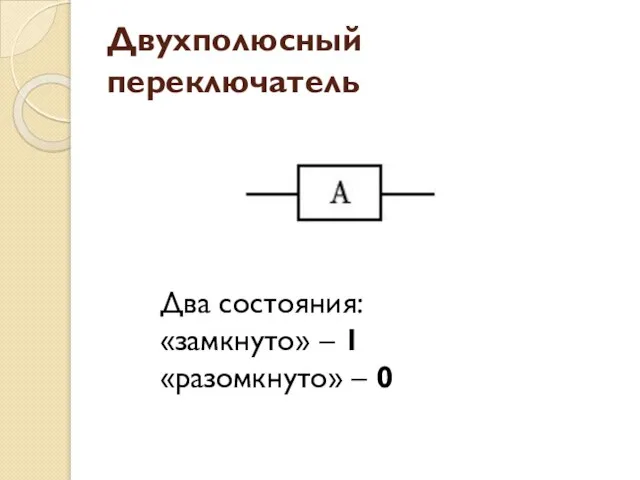
- 73. Двухполюсный переключатель Два состояния: «замкнуто» – 1 «разомкнуто» – 0
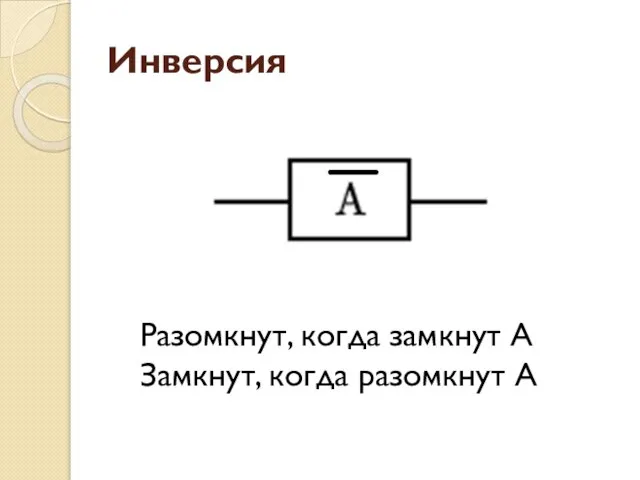
- 74. Инверсия Разомкнут, когда замкнут А Замкнут, когда разомкнут А
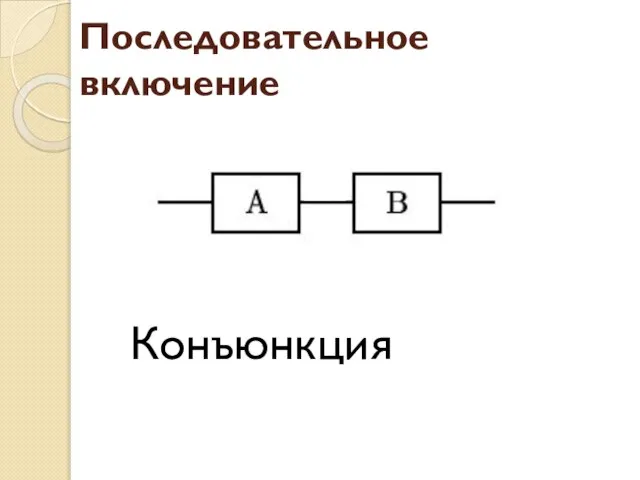
- 75. Последовательное включение Конъюнкция
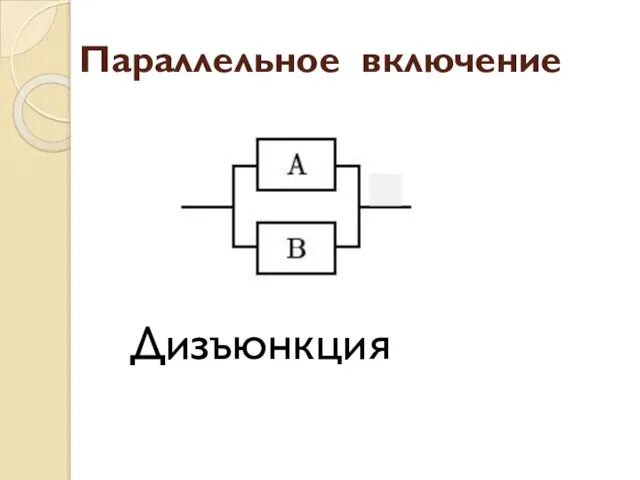
- 76. Параллельное включение Дизъюнкция
- 77. Множество высказываний и множество переключательных схем одинаково устроены (изоморфны) Это можно использовать при решении задач
- 78. Анализ схем Для данной схемы строим формулу Упрощаем её с помощью законов логики Строим более простую
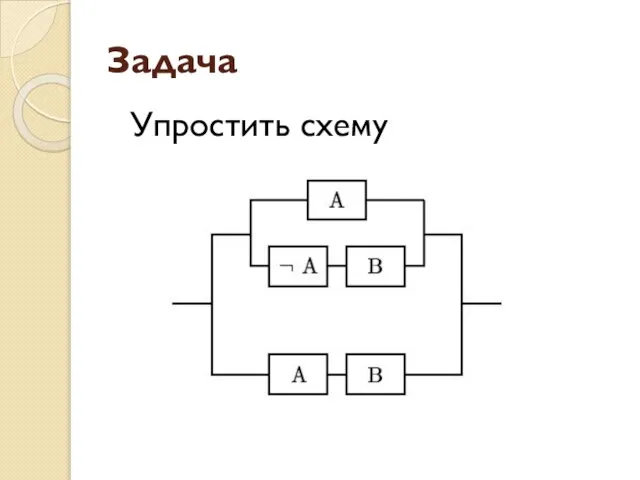
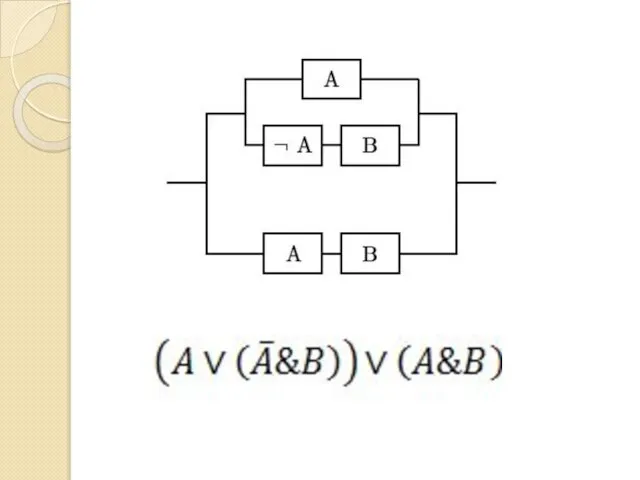
- 79. Задача Упростить схему
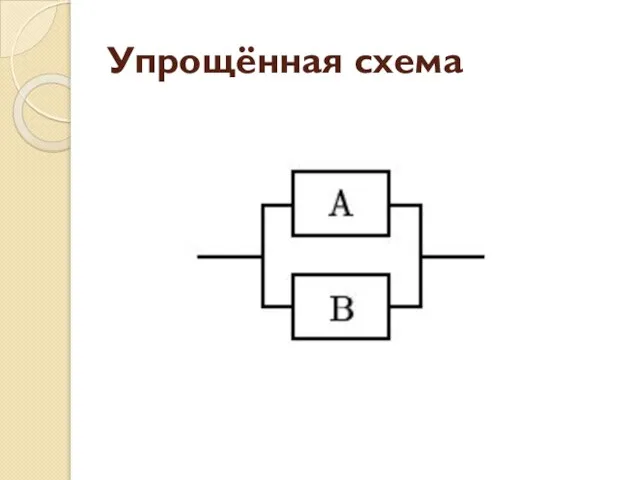
- 82. Упрощённая схема
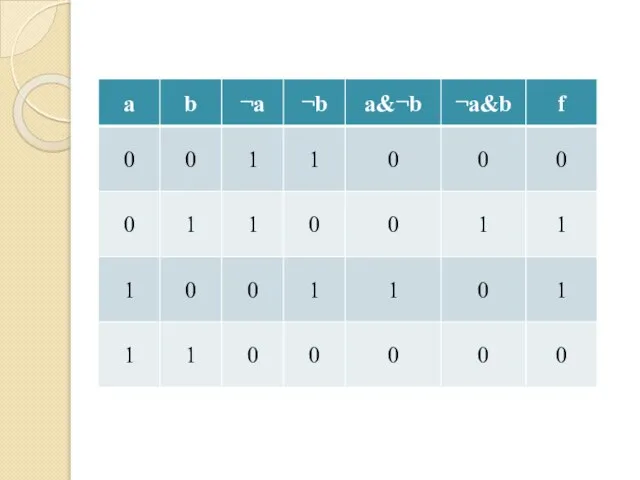
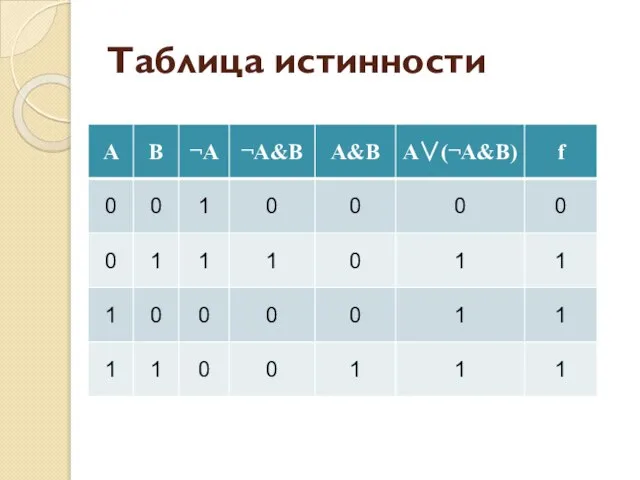
- 83. Таблица истинности
- 85. Скачать презентацию


















































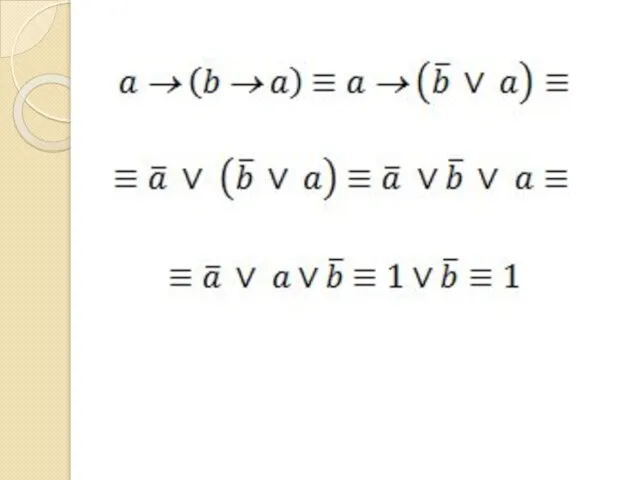

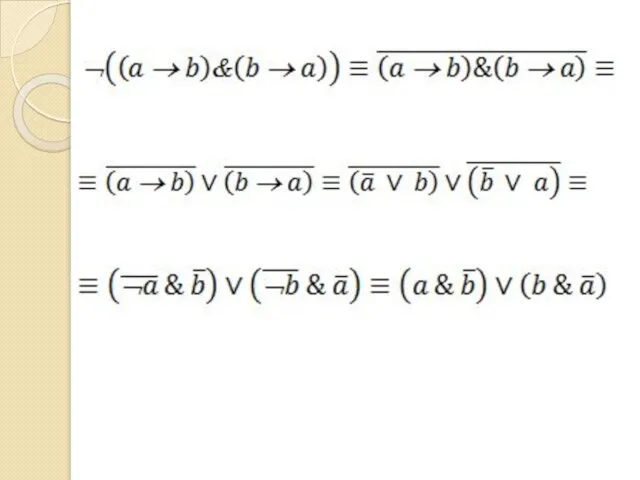



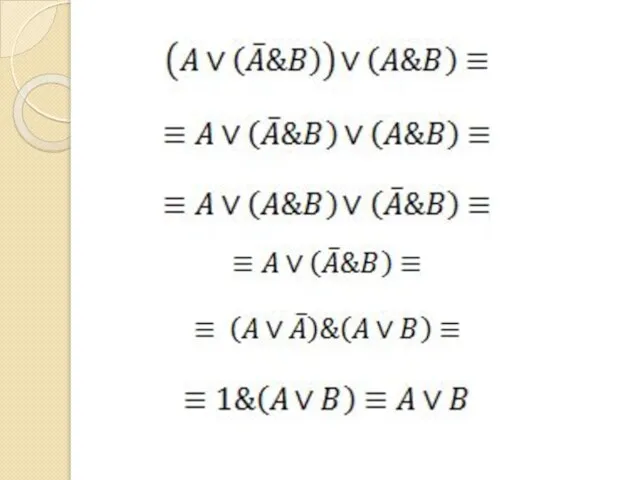
 Презентация на тему Восточная Сибирь
Презентация на тему Восточная Сибирь  Упрощение выражений
Упрощение выражений Проект «Аналогия» был запущен нами более десяти лет назад и возник как плод сочетания потенциалов юриста и бухгалтера с целью реше
Проект «Аналогия» был запущен нами более десяти лет назад и возник как плод сочетания потенциалов юриста и бухгалтера с целью реше Генеалогия
Генеалогия Колизей в Риме
Колизей в Риме 1С-Битрикс: Корпоративный портал
1С-Битрикс: Корпоративный портал Слова антонимы (Противоположности)
Слова антонимы (Противоположности) Cisco Solution Technology Integrator Сетевая безопасность для вертикальных рынков Решения для коммуникационных провайдеров СТАНДАРТ СЕТЕВОЙ БЕЗО
Cisco Solution Technology Integrator Сетевая безопасность для вертикальных рынков Решения для коммуникационных провайдеров СТАНДАРТ СЕТЕВОЙ БЕЗО Китайский новый год
Китайский новый год 20 причин любить Рёму
20 причин любить Рёму Путь. Перемещение. Определение координаты движущегося тела
Путь. Перемещение. Определение координаты движущегося тела Pancakes day
Pancakes day Критерии и методика отнесения документов к категории для служебного пользования
Критерии и методика отнесения документов к категории для служебного пользования Учебные видеоролики, как ресурс саморазвития
Учебные видеоролики, как ресурс саморазвития Система Box-Design & Nevo
Система Box-Design & Nevo Рекомендуемые подходы определения страховых резервов по договорам страхования жизни На основе Проекта Минфина Правил формирова
Рекомендуемые подходы определения страховых резервов по договорам страхования жизни На основе Проекта Минфина Правил формирова Дома гороскопа
Дома гороскопа Сложение и вычитание десятичных дробей.
Сложение и вычитание десятичных дробей. Судьба старославянизмов в русском языке
Судьба старославянизмов в русском языке Подготовка к написанию изложения по рассказу Л.Н.Толстого «Акула»
Подготовка к написанию изложения по рассказу Л.Н.Толстого «Акула» Обобщающий урок по теме:
Обобщающий урок по теме: Маркетинговые исследования
Маркетинговые исследования  Факторы развития когнитивных способностей в процессе обучения
Факторы развития когнитивных способностей в процессе обучения Доступ к данным на основе ado
Доступ к данным на основе ado Весна. Детские рисунки
Весна. Детские рисунки Декларация на товары
Декларация на товары Химическое действие света. Фотография
Химическое действие света. Фотография Моделирование, как метод познания (10 класс)
Моделирование, как метод познания (10 класс)