Алгоритмизация_Л1

Понятие алгоритма
Алгоритм-
последовательность элементарных действий, формальное выполнение которой
приводит к верному решению задачи за конечное время.
Исполнитель –
Одушевлённый или неодушевлённый объект, выполняющий последовательность элементарных действия.
Элементарное действие –
действие, которое исполнитель может выполнять без дополнительного обучения.

Запись алгоритма, кодирование алгоритма
Запись алгоритма –
фиксация алгоритма в бумажной или электронной форме с использованием неформального набора правил
Кодирование алгоритма –
фиксация алгоритма в бумажной или электронной форме с использованием формального набора правил
Набор правил является формальным, если неописанные правилами действия выполнять запрещено.
Набор правил является неформальным, если неописанные правилами действия можно выполнять произвольным образом.

Программирование
АЛГОРИТМ =ПРОГРАММА
Программирование – разработка алгоритма

Способы записи алгоритма
Способы записи алгоритма:
Блок-схема
Пошаговая процедура.
Псевдокод.
Состояния алгоритма:
Прямой ход.
Разветвление.
Передача управления вперёд / назад.
Прямой ход:
последовательное выполнение элементарных действий.
Разветвление:
выбор одного их множества элементарных действий для выполнения.
Передача управления:
переход к указанной элементарной операции, не следующей по порядку за текущей.
вперёд – если указанная операция расположена после текущей;
назад – если указанная операция расположена перед текущей.

Способы записи алгоритма
При вычислении математических выражений должно быть указано:
Формула для вычисления результата.
Место, в котором необходимо сохранить результат.
Переменная – символьное обозначение места хранения числовых, текстовых или логических значений, а так же составных объектов.
Значение переменной – число, текст, логическое значение или составной объект.
Прибавить к переменой Х единицу – неверная запись! Не указано место хранения результата!
Увеличить значение переменной Х на единицу – верная запись, эквивалентная Х = Х + 1.

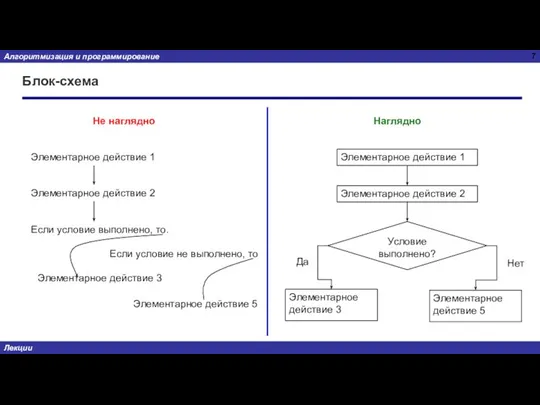
Блок-схема
Не наглядно
Наглядно
Элементарное действие 1
Элементарное действие 2
Если условие выполнено, то.
Если условие не выполнено, то
Элементарное действие 3
Элементарное действие 5
Элементарное действие 1
Элементарное действие 2
Условие выполнено?
Элементарное
действие 3
Элементарное
действие 5
Да
Нет

Пошаговая процедура
ШАГ1: формальное действие 1
ШАГ2: формальное действие 2
ШАГ3: если условие выполнено, то перейти к шагу 4, иначе перейти к шагу 6
ШАГ4: формальное действие 3
ШАГ5: перейти к шагу 7
ШАГ6: формальное действие 5
ШАГ7: ….

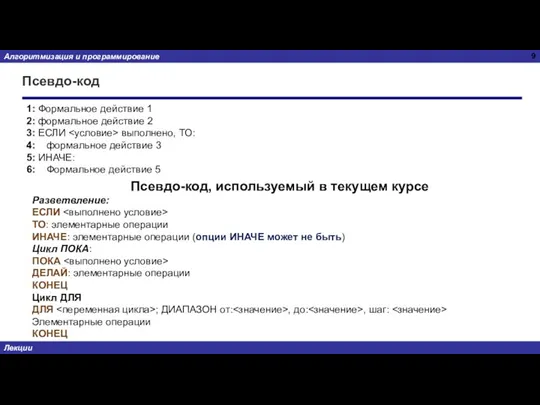
Псевдо-код
1: Формальное действие 1
2: формальное действие 2
3: ЕСЛИ <условие> выполнено, ТО:
4: формальное действие 3
5: ИНАЧЕ:
6: Формальное действие 5
Псевдо-код, используемый в текущем курсе
Разветвление:
ЕСЛИ <выполнено условие>
ТО: элементарные операции
ИНАЧЕ: элементарные операции (опции ИНАЧЕ может не быть)
Цикл ПОКА:
ПОКА <выполнено условие>
ДЕЛАЙ: элементарные операции
КОНЕЦ
Цикл ДЛЯ
ДЛЯ <переменная цикла>; ДИАПАЗОН от:<значение>, до:<значение>, шаг: <значение>
Элементарные операции
КОНЕЦ

Элементарные действия для исполнителя «Компьютер»
Арифметические действия:
сложение ( + )
вычитание ( - )
умножение ( * )
деление ( / )
Логические действия:
логическое И ( & )
логическое ИЛИ ( | )
отрицание НЕ ( not )
Действия сравнения:
больше (>)
меньше (<)
равно (=)
Действия ввода и вывода:
ввод (input)
вывод (output)
Ввод десятичных чисел является элементарной операцией УСЛОВО!
Действие сохранения значения:
присвоить значение переменной ( = )
ввод ( input )

Пример алгоритма
Разработать алгоритм - значит представить решение исходной задачи в виде последовательности элементарных действий.
Задача: вычислить значение переменной X равное сумме значений переменных A и B и вывести результат на экран монитора.
Алгоритм:
1: присвоить значение переменной А
2: присвоить значение переменной B
3: выполнить сложение A + B
4: сохранить результат сложения в перемой X
5: вывести значение переменной Х
Запись алгоритма c помощью псевдо-кода:
input A
input B
X = А + B
output X

Состояние алгоритма
Состояние алгоритма
определяется значениями переменных, используемых в алгоритме
Цикл
многократное повторение последовательности элементарных действий.
Инварианта цикла
набор переменных, задающих начальные условия для очередной итерации цикла.
Инварианта цикла проходит три состояния:
инициализация
повторение
окончание

Агрегатные данные типа МАССИВ.
Массив – упорядоченный набор однотипных значений, к каждому из которых можно обратиться, указав его индекс (порядковый номер).
Элемент 1
Значение элемента 1
Индекс элемента 1
Элемент 2
Значение элемента 2
Индекс элемента 2
…
Элемент N
Значение элемента n
Индекс элемента n
Массив A
Обращение к значению элемента массива с индексом m: A[m]

Агрегатные данные типа МАССИВ.
Свойства массива:
Значения элементов массива существуют физически.
Индексы – виртуальные величины.
Каждый элемент массива можно рассматривать как самостоятельную переменную с именем A[m].
Имя переменной может формироваться в ходе выполнения алгоритма.
К массиву нельзя обратиться по его имени!
A = 1 – НЕВЕРНО!
A[3] = 1 – ВЕРНО! (в переменной А[3] будет хранится значение 1)

Алгоритм подсчёта количества элементов массива с заданными значениями
Задача
Задан массив с именем А, состоящий из N элементов.
Определить, сколько элементов удовлетворяют условию COND.
Запись COND( X ) означает проверку условия для значения переменной Х.
Пример
COND ПЕРЕМЕННАЯ > 5
COND( 3 ) – ЛОЖЬ (3 > 5)
COND( 9 ) – ИСТИНА ( 9 > 5 )
Y = 7
COND( Y ) – ИСТИНА (7 > 5)
Z = 2
COND( Z ) – ЛОЖЬ (2 > 5)

Алгоритм подсчёта количества элементов массива с заданными значениями
Идея реализации алгоритма, решающего задачу:
В переменной count будет хранится значение, равное количеству элементов массива, удовлетворяющих заданному условию.
В переменой idx будет хранится индекс элемента массива
Проверяем: удовлетворяет значение элемента массива с индексом idx условию COND?
Если удовлетворяет, то увеличиваем значение переменной count на 1.
Повторяем проверку для всех элементов массива (в алгоритме будет цикл!).
Псевдо-код алгоритма
count = 0
idx = 0
ПОКА idx < N
ДЕЛАЙ:
ЕСЛИ COND( A[idx] )
ТО:
count = count +1
idx = idx + 1
КОНЕЦ
ИНВАРИАНТА ЦИКЛА:
count, idx

Алгоритм подсчёта элементов массива с заданными значениями
Инициализация инварианты:
count = 0 (нет элементов удовлетворяющих COND)
idx =0 (будет обрабатываться элемент массива с номером 0)
Повторение инварианты
после первого цикла:
значение count содержит количество элементов (0 или 1), удовлетворяющих COND.
idx = 1 (указывает на то, что следующим будет обрабатываться элемент массива с номером 1).
после второго цикла:
значение count содержит количество элементов (от 0 до 2), удовлетворяющих COND.
idx = 2 (указывает на то, что следующим будет обрабатываться элемент массива с номером 2).
...
Окончание цикла
idx = N
count содержит значение, равное количеству элементов, удовлетворяющих COND

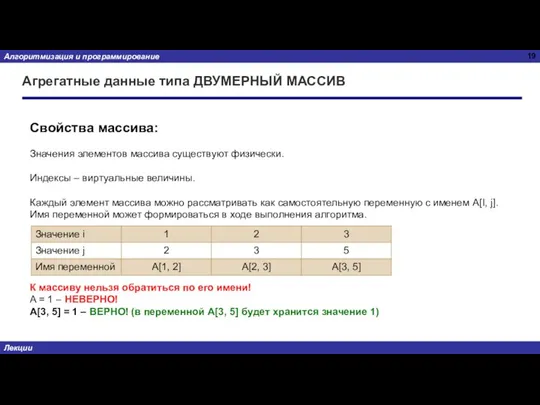
Агрегатные данные типа ДВУМЕРНЫЙ МАССИВ
Обращение к значению элемента массива с индексами I, j: A[I, j]

Агрегатные данные типа ДВУМЕРНЫЙ МАССИВ
Свойства массива:
Значения элементов массива существуют физически.
Индексы – виртуальные величины.
Каждый элемент массива можно рассматривать как самостоятельную переменную с именем A[I, j].
Имя переменной может формироваться в ходе выполнения алгоритма.
К массиву нельзя обратиться по его имени!
A = 1 – НЕВЕРНО!
A[3, 5] = 1 – ВЕРНО! (в переменной А[3, 5] будет хранится значение 1)

Алгоритм подсчёта количества элементов двумерного массива с заданными значениями
Задача
Задан двумерный массив с именем В, состоящий из N строк и M столбцов (N * M элементов).
Определить, сколько элементов удовлетворяют условию COND.
Идея реализации алгоритма, решающего задачу:
В переменной count будет хранится значение, равное количеству элементов массива, удовлетворяющих заданному условию.
В переменой idx_1 будет хранится номер строки.
В переменой idx_2 будет хранится номер столбца.
Проверяем: удовлетворяет значение элемента массива с индексами idx_1, idx_2 условию COND? Если удовлетворяет, то увеличиваем значение переменной count на 1.
Повторяем проверку для всех элементов массива (в алгоритме будут два цикла!).

Алгоритм подсчёта количества элементов двумерного массива с заданными значениями
Псевдо-код алгоритма
count = 0
idx_1 = 0
idx_2 = 0
ПОКА idx_1 < N
ДЕЛАЙ:
ПОКА idx_2 < M
ЕСЛИ COND( A[idx_1, idx_2] )
ТО:
count = count +1
idx_2 = idx_2 + 1
КОНЕЦ
idx_2 = idx_2 + 1
КОНЕЦ
ИНВАРИАНТА ЦИКЛА:
count, idx_1, idx_2

Алгоритм подсчёта количества элементов двумерного массива с заданными значениями
Инициализация инварианты:
count = 0 (нет элементов удовлетворяющих COND)
idx_1 = 0, idx_2 = 0 (будет обрабатываться элемент массива с индексами 0,0)
Повторение инварианты
после первого внутреннего цикла:
значение count содержит количество элементов (0 или 1), удовлетворяющих COND.
idx_1 = 0, idx_2 = 1 (указывает на то, что следующим будет обрабатываться элемент массива с индексами 0, 1).
после первого внешнего цикла:
значение count содержит количество элементов (от 0 до М), удовлетворяющих COND.
idx_1 = 1, idx_2 = 0 (указывает на то, что следующим будет обрабатываться элемент массива с индексами 1, 0).
Окончание цикла
idx_1 = N, idx_2 = M
count содержит значение, равное количеству элементов, удовлетворяющих COND

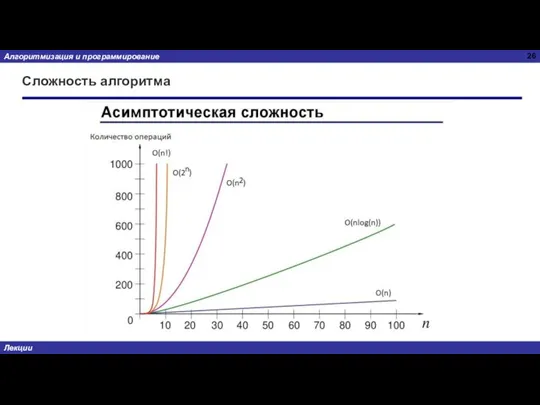
Сложность алгоритма
Сложность алгоритма
величина, показывающая, как связано количество элементарных операций, необходимых для решения задачи, с объёмом входных данных.
Обозначается O(математическое выражение)
Примеры:
O(n) при увеличении объёма входных данных в 2 раза, количество элементарных операций увеличится в 2 раза.
O(n2) при увеличении объёма входных данных в 2 раза, количество элементарных операций увеличится в 4 раза.
O(log(n)) при увеличении объёма входных данных в 256 раз, количество элементарных операций увеличится в 8 раза.

Сложность алгоритма
Псевдо-код алгоритма подсчёта количества элементов, удовлетворяющих условию COND в одномерном массиве
count = 0
idx = 0
ПОКА idx < N
ДЕЛАЙ:
ЕСЛИ COND( A[idx] )
ТО:
count = count +1
idx = idx + 1
КОНЕЦ
Будет N проходов цикла
Каждая
из
элементарных операций
повторится N раз
Сложность алгоритма O(N)

Сложность алгоритма
Псевдо-код алгоритма подсчёта количества элементов, удовлетворяющих условию COND в двумерном массиве
count = 0
idx_1 = 0
idx_2 = 0
ПОКА idx_1 < N
ДЕЛАЙ:
ПОКА idx_2 < M
ДЕЛАЙ:
ЕСЛИ COND( A[idx_1, idx_2] )
ТО:
count = count +1
idx_2 = idx_2 + 1
КОНЕЦ
idx_2 = idx_2 + 1
КОНЕЦ
Будет N проходов цикла
Будет M проходов цикла
Каждая
из
элементарных операций
повторится N * M раз
Сложность алгоритма O( N*M)
Для квадратного массива O(N2)

Сложность алгоритма

Сумма значений одномерного массива
Задача
Задан одномерный массив с именем А, состоящий из N элементов.
Вычислить сумму значений элементов массива.
Идея реализации алгоритма, решающего задачу:
В переменной Total будет хранится текущая сумма значений элементов массива.
В переменой idx будет хранится индекс текущего элемента массива.
Прибавляем значение текущего элемента массива к значению Total, сохраняем результат в Total.
Повторяем суммирование для всех элементов массива (в алгоритме будет цикл!).
Псевдо-код алгоритма подсчёта суммы
Total = 0
idx = 0
ПОКА idx < N
ДЕЛАЙ:
Total = Total + A[idx]
idx = idx + 1
КОНЕЦ
Будет N проходов цикла.
Каждая из
элементарных операций повторится N раз
Сложность алгоритма O( N)
Инварианта цикла:
Total, idx

Сумма значений одномерного массива
Инициализация инварианты:
Total = 0 (До начала суммирования значение суммы равно 0)
idx =0 (будет обрабатываться элемент массива с номером 0)
Повторение инварианты
после первого цикла:
значение Total равно значению нулевого элемента массива.
idx = 1 (указывает на то, что следующим будет обрабатываться элемент массива с номером 1).
после второго цикла:
значение Total равно сумме значений нулевого и первого элементов массива.
idx = 2 (указывает на то, что следующим будет обрабатываться элемент массива с номером 2).
...
Окончание цикла
idx = N
Total содержит сумму значений элементов массива

Поиск максимального значения в одномерном массиве
Задача
Задан массив с именем А, состоящий из N элементов.
Определить, максимальное среди всех значений элементов массива.
Идея реализации алгоритма, решающего задачу:
Local – максимальное значение
среди элементов с 0 по i
Local – максимальное значение
среди элементов с 0 по i + 1
Если A[I + 1] > Local, то

Поиск максимального значения в одномерном массиве
Идея реализации алгоритма, решающего задачу, продолжение
Переменная idx хранит номер текущего обрабатываемого элемента массива.
Значение переменной Local равно максимальному среди значений элементов массива с номерами
0 … idx -1
Если A[idx] > Local, то значение A[idx] максимальное среди значений элементов с номерами 0 … idx :
Local = A[idx]
Если A[idx] <= Local, то значение Local максимальное среди значений элементов с номерами 0 … idx
Значение Local не изменяется.
Псевдо-код алгоритма
Local = A[0]
idx = 1
ПОКА idx < N
ДЕЛАЙ:
ЕСЛИ A[idx] > Local
ТО:
Local = A[idx]
idx = idx + 1
КОНЕЦ
ИНВАРИАНТА ЦИКЛА:
Local, idx
Будет N проходов цикла.
Каждая из
элементарных операций
повторится N раз
Сложность алгоритма O( N)

Поиск максимального значения в одномерном массиве
Инициализация инварианты:
Local = A[0] (До первого повторения цикла, значение нулевого элемент массива считается максимальным, т.к. значения других элементов пока не анализировались)
idx =1 (будет обрабатываться элемент массива с номером 1. Элемент массива с номером 0 уже учтён, при задании начального значения переменной Local)
Повторение инварианты
после первого цикла:
значение Local равно максимальному значению среди нулевого и первого элементов массива.
idx = 2 (указывает на то, что следующим будет обрабатываться элемент массива с номером 2).
после второго цикла:
значение Local равно максимальному значению среди нулевого, первого и второго элементов массива.
idx = 3 (указывает на то, что следующим будет обрабатываться элемент массива с номером 3).
...
Окончание цикла
idx = N
Local содержит максимальное значение среди всех элементов массива.

Поиск в одномерном массиве максимального значения среди элементов, удовлетворяющих заданному условию
Задача
Задан массив с именем А, состоящий из N элементов.
Определить, максимальное среди значений элементов массива, таких что COND(A[i]) истинно,
i = 0 … N - 1.
Local – максимальное значение
среди элементов с 0 по i, для которых COND(A[j]) истинно
Local – максимальное значение
среди элементов с 0 по i + 1, для которых COND(A[j]) истинно
Если A[I + 1] > Local, то
j = 0, 1, …, i
j = 0, 1, …, I + 1

Поиск в одномерном массиве максимального значения среди элементов, удовлетворяющих заданному условию
Псевдо-код алгоритма (вариант 1)
Local = минимально возможному значению типа
idx = 1
ПОКА idx < N
ДЕЛАЙ:
ЕСЛИ COND(A[idx]) & A[idx] > Local
ТО:
Local = A[idx]
idx = idx + 1
КОНЕЦ
ИНВАРИАНТА ЦИКЛА:
Local, idx
Будет N проходов цикла.
Каждая из
элементарных операций
повторится N раз
Сложность алгоритма O( N)

Поиск в одномерном массиве максимального значения среди элементов, удовлетворяющих заданному условию
Псевдо-код алгоритма (вариант 2)
idx = 0
ПОКА not(COND(A[idx])
ДЕЛАЙ:
idx = idx + 1
КОНЕЦ
Local = A[idx]
idx = idx + 1
ПОКА idx < N
ДЕЛАЙ:
ЕСЛИ COND(A[idx]) & A[idx] > Local
ТО:
Local = A[idx]
idx = idx + 1
КОНЕЦ
ИНВАРИАНТА ЦИКЛА 1:
idx
ИНВАРИАНТА ЦИКЛА 2:
Local, idx
В двух циклах суммарно будет N проходов.
Каждая из
элементарных операций
повторится N раз
Сложность алгоритма O( N)

Поиск в одномерном массиве максимального значения среди элементов, удовлетворяющих заданному условию (вариант 1)
Инициализация инварианты:
Local = минимально возможному значению типа для элементов массива.
idx = 0 (будет обрабатываться элемент массива с номером 0. Ни один из элементов массива не учтён).
Повторение инварианты
после первых циклов, в которых COND(A[idx]) ложно:
значение Local не изменится.
idx = idx + 1 (указывает на переход к следующему элементу массива).
после первого цикла, в котором COND(A[idx]) истинно:
значение Local равно A[idx].
idx = idx + 1 (указывает на переход к следующему элементу массива).
после всех последующих циклов
значение Local равно максимальному среди элементов массива для которых COND(A[idx]) истинно.
idx = idx + 1 (указывает на переход к следующему элементу массива).
Окончание цикла
idx = N
Local содержит максимальное значение среди всех элементов массива, для которых COND(A[idx]) истинно.

Поиск в одномерном массиве максимального значения среди элементов, удовлетворяющих заданному условию (вариант 2)
Инициализация инварианты цикла 1:
idx = 0 (будет обрабатываться элемент массива с номером 0).
Повторение инварианты
после всех повторений цикла 1, для которых COND(A[idx]) ложно
idx = idx + 1 (переход к следующему элементу массива).
Окончание цикла 1
COND(A[idx]) истинно
Инициализация инварианты цикла 2:
Local = A[idx] (начальное значение Local равно значению первого элемента, удовлетворяющего COND)
idx = idx + 1 (будет обрабатываться элемент массива, следующий за первым, для которого COND(A[idx]) истинно.
Повторение инварианты цикла 2
после первого повторения:
Local не изменяется, если:
COND(A[idx]) ложно;
COND(A[idx]) истинно и Local <= A[idx]
Local = A[idx], если COND(A[idx]) истинно и Local > A[idx]
idx = idx + 1 (переход к следующему элементу массива).