Содержание
- 2. Топологическая сортировка
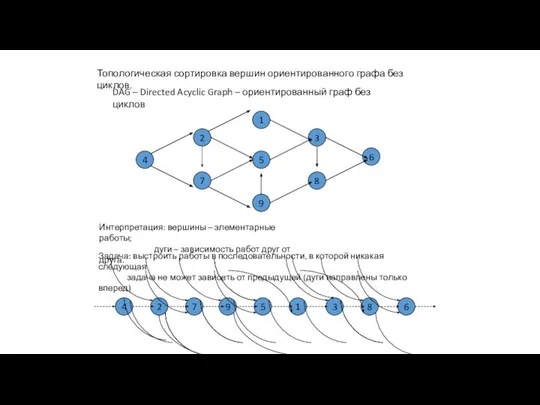
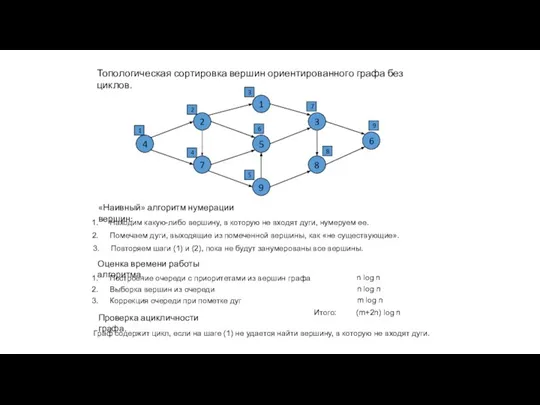
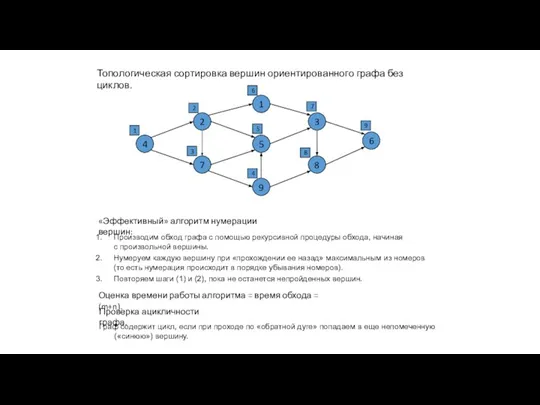
- 3. Топологическая сортировка вершин ориентированного графа без циклов. DAG – Directed Acyclic Graph – ориентированный граф без
- 4. Топологическая сортировка вершин ориентированного графа без циклов. 1 5 9 2 7 3 8 4 6
- 5. Топологическая сортировка вершин ориентированного графа без циклов. 1 5 9 2 7 3 8 4 6
- 6. Алгоритм Флойда - Уоршелла
- 7. Алгоритм Флойда - Уоршелла Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом В отличии от
- 8. Обозначения Перенумеруем вершины графа целыми числами от 1 до N. Обозначим через di,jm длину кратчайшего пути
- 9. Обозначения Обозначим через Dm матрицу размера NxN, элемент (i,j) которой совпадает с di,jm. Если в исходном
- 10. Суть алгоритма Флойда заключается в проверке того, не окажется ли путь из вершины i в вершину
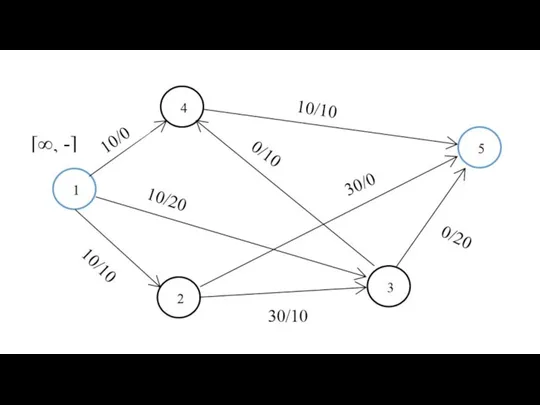
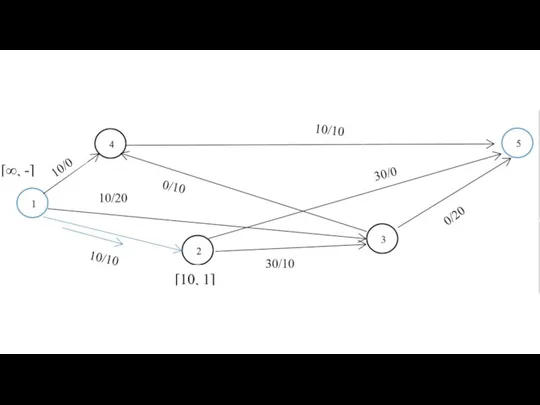
- 11. Этап 1. Перенумеровать вершины графа от 1 до N, определить матрицу D0, каждый элемент di,j0 которой
- 12. Матрицу S0, в которой будем запоминать последовательность вершин в кратчайшем пути, заполним так: sij = j
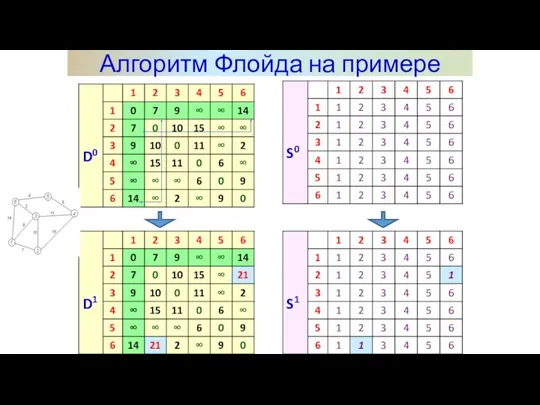
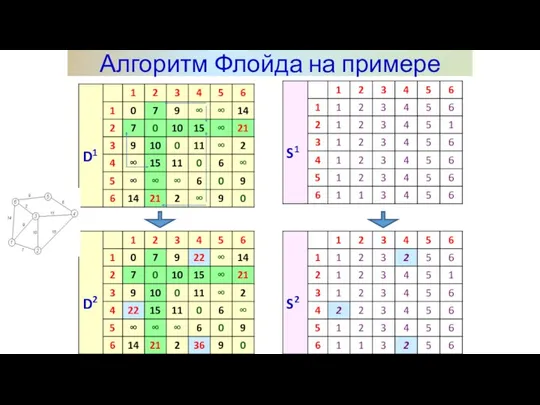
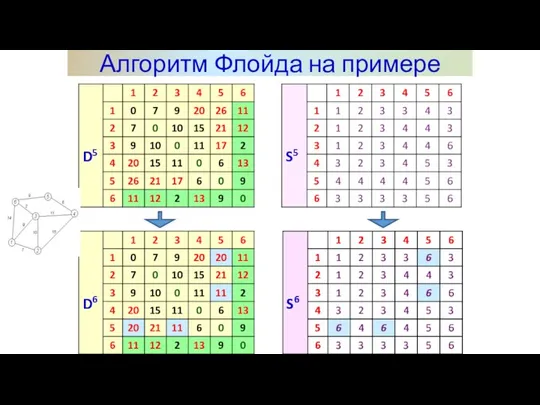
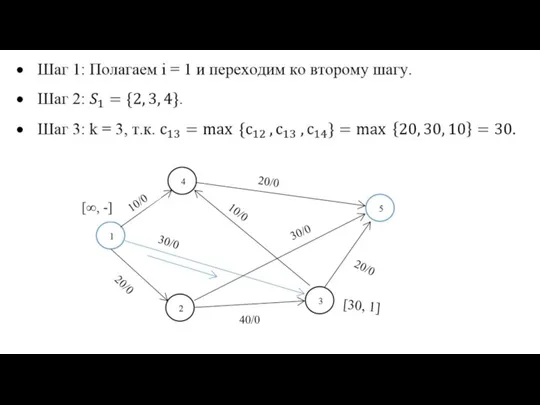
- 13. Алгоритм Флойда на примере Задаём строку m и столбец m как ведущую строку и ведущий столбец.
- 14. Алгоритм Флойда на примере
- 15. Алгоритм Флойда на примере
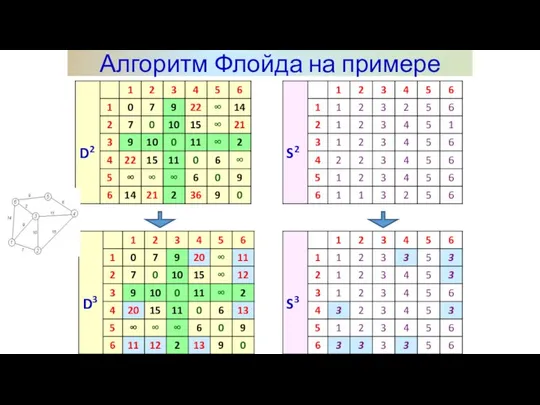
- 16. Алгоритм Флойда на примере
- 17. Алгоритм Флойда на примере
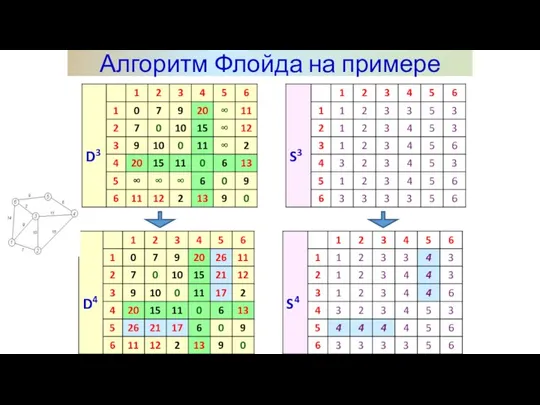
- 18. Алгоритм Флойда на примере
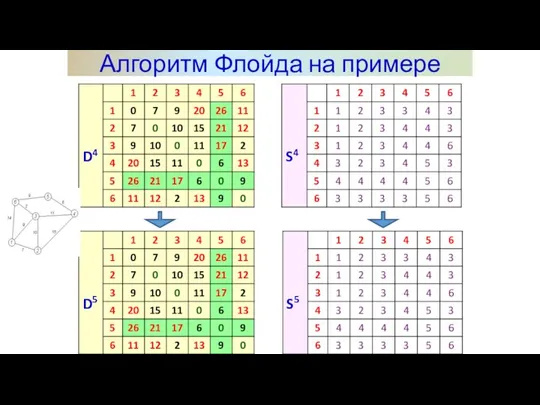
- 19. Алгоритм Флойда на примере
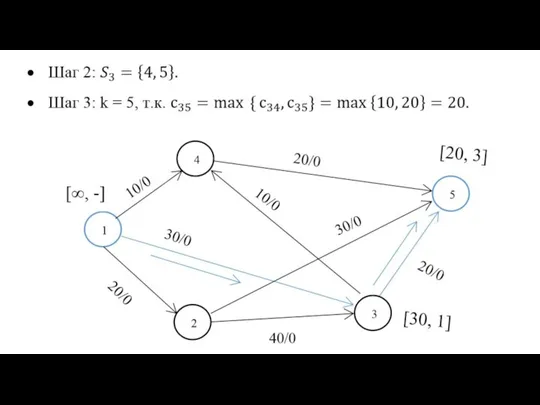
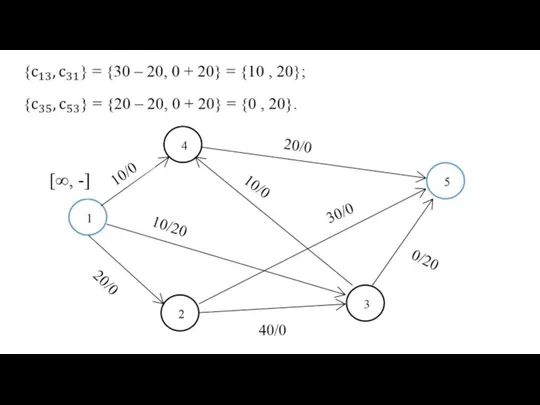
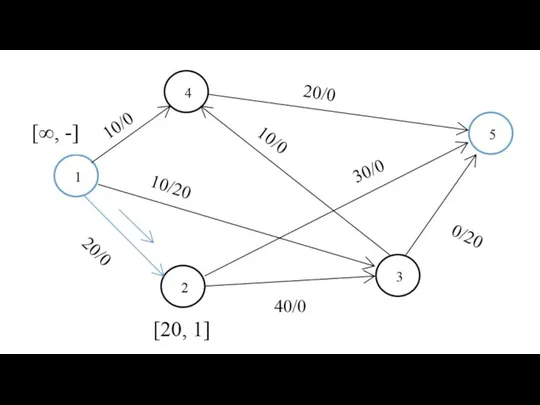
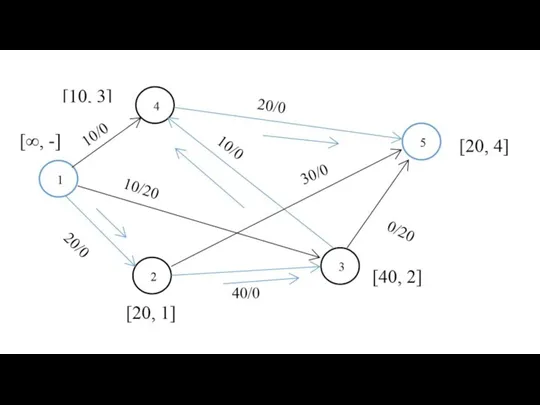
- 20. Алгоритм Флойда на примере Последний этап. После реализации N этапов алгоритма определение по матрицам Dn и
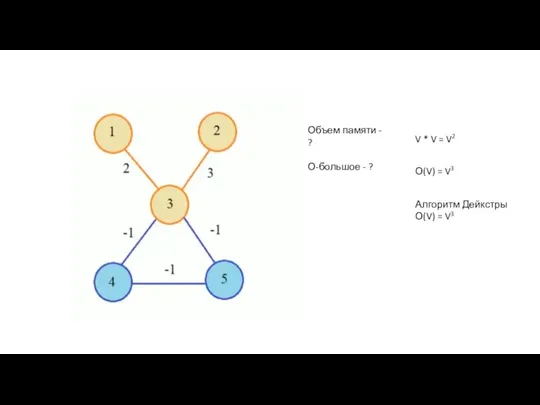
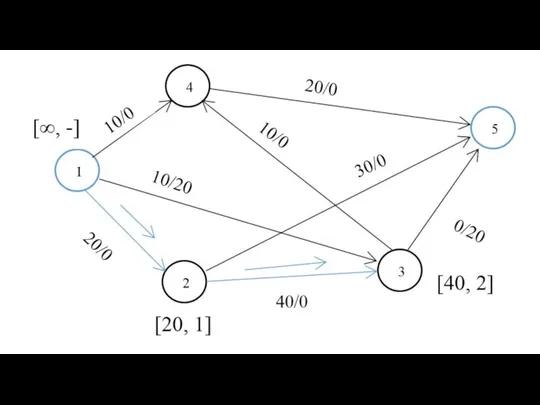
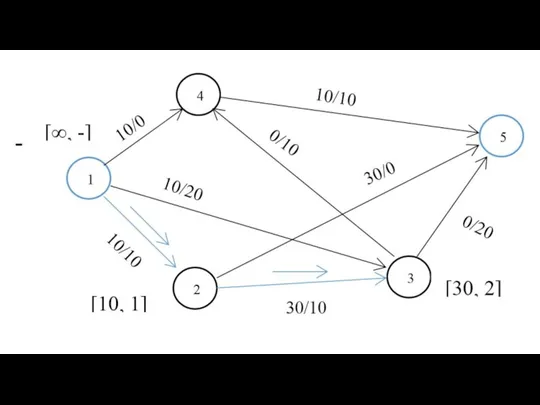
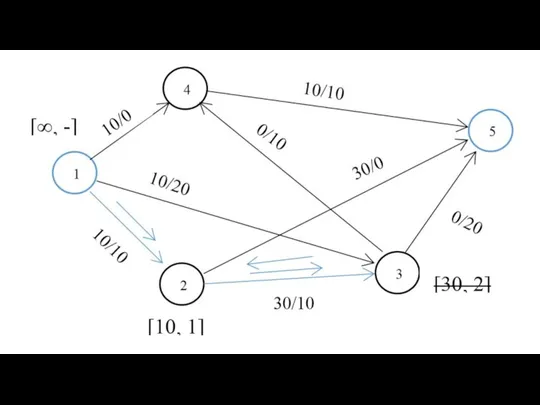
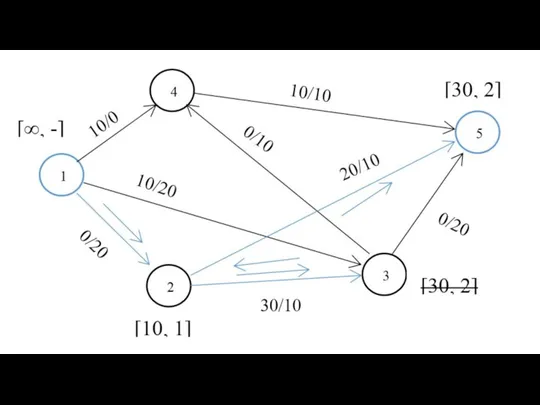
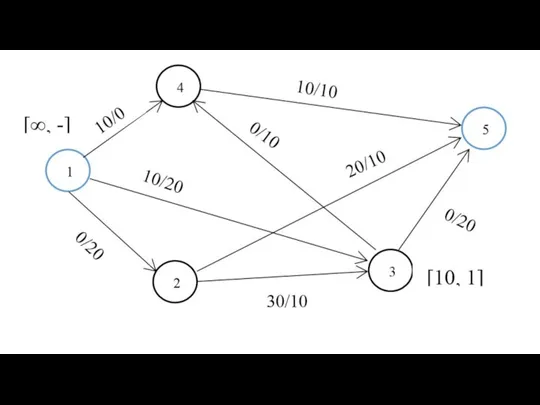
- 21. d25 = 21 Путь: 2->4 ->5 d51 = 20 Путь: 5->6 ->3 -> 1 Алгоритм Флойда
- 22. Объем памяти - ? О-большое - ? V * V = V2 О(V) = V3 Алгоритм
- 24. Волновой алгоритм (Алгоритм Ли)
- 25. Рассматривается алгоритм построения ортогонального пути. Алгоритм состоит из двух частей. В первой от источника к приемнику
- 27. Инициализация Пометить стартовую ячейку d := 0 Распространение волны ЦИКЛ ДЛЯ каждой ячейки X, помеченной числом
- 32. При обратном ходе в путь включается по одной ячейке каждого шага распространения волны. При выборе из
- 33. Алгоритм Форда – Фалкерсона
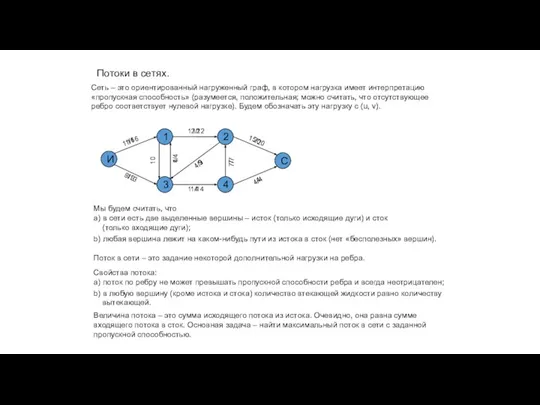
- 34. Потоки в сетях. И 1 2 3 С 4 Сеть – это ориентированный нагруженный граф, в
- 35. Потоки в сетях. И 1 2 3 С 4 Пусть задана сеть и поток в ней.
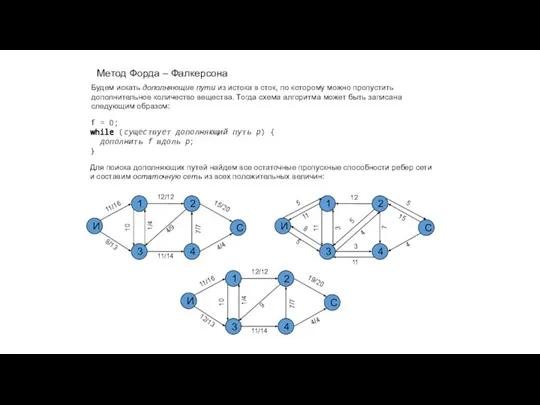
- 36. Метод Форда – Фалкерсона И 1 2 3 С 4 Будем искать дополняющие пути из истока
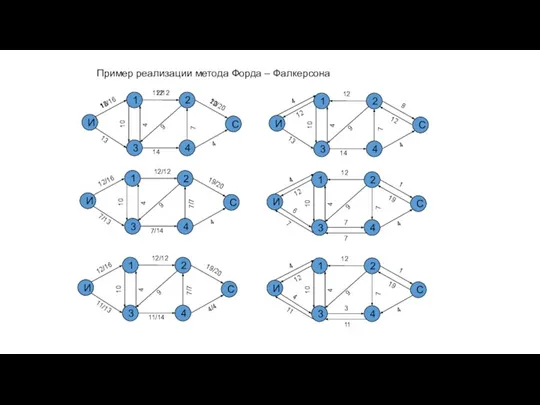
- 37. Пример реализации метода Форда – Фалкерсона И 1 2 3 С 4 10 16 12 4
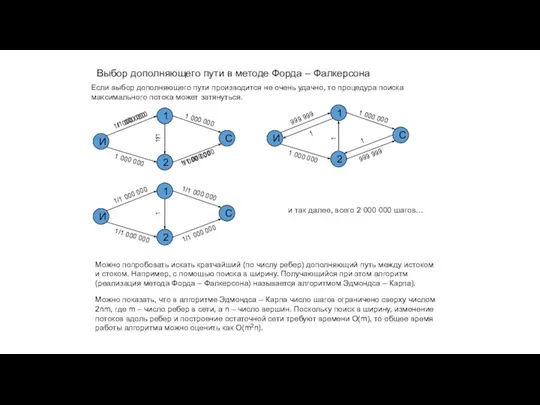
- 38. Выбор дополняющего пути в методе Форда – Фалкерсона И 1 2 С 1 1 000 000
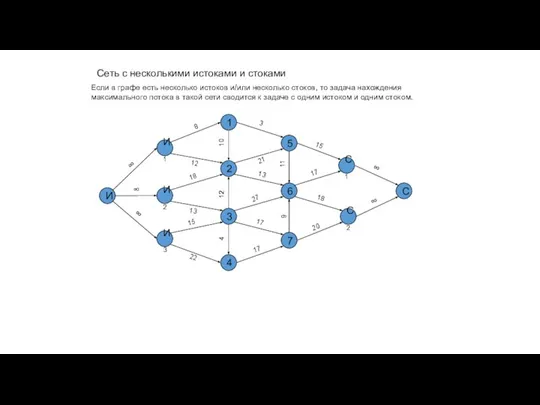
- 39. Сеть с несколькими истоками и стоками И1 1 2 С1 10 3 Если в графе есть
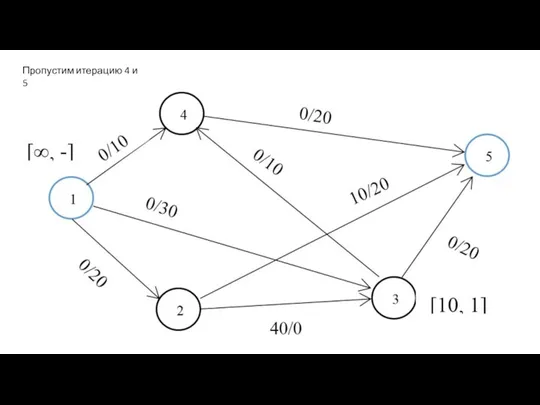
- 53. Пропустим итерацию 4 и 5
- 54. Минимальное остовное дерево (МОД)
- 55. … Остовной связный подграф – подграф графа G, который содержит все его вершины и каждая вершина
- 56. Цикломатическое число γ показывает, сколько ребер нужно удалить из графа, чтобы в нем не осталось циклов
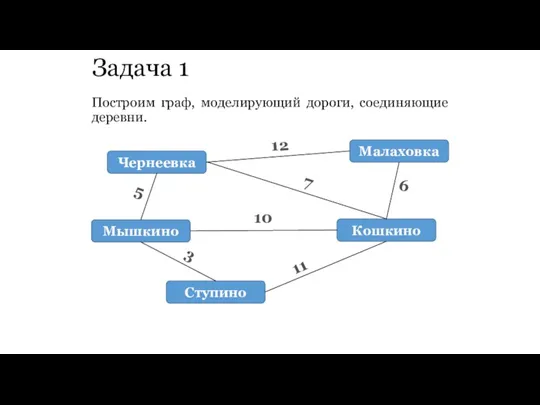
- 57. Задача 1 В некотором районе было решено провести газопровод между пятью деревнями. От Кошкино до Мышкино
- 58. Задача 1 Построим граф, моделирующий дороги, соединяющие деревни.
- 59. Задача 1 Задача сводится к построению остовного связного дерева минимального веса. Рассчитаем цикломатическое число. m (количество
- 60. Алгоритм Прима Начало алгоритма: с произвольной вершины К текущему дереву присоединяется смежная вершина с кратчайшим ребром.
- 61. Алгоритм Прима Пусть дан взвешенный неориентированный граф. Для построения минимального остовного дерева необходимо: 1. Представить граф
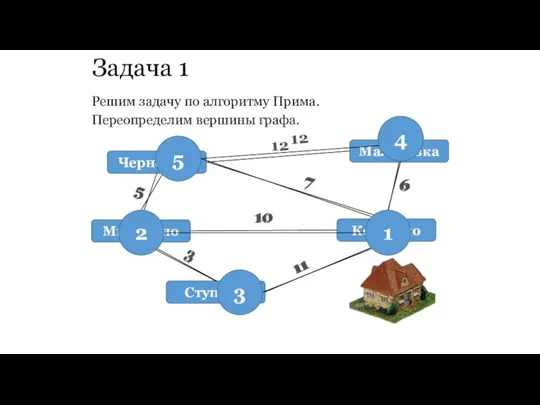
- 62. Задача 1 Решим задачу по алгоритму Прима. Переопределим вершины графа.
- 63. Задача 1 Представим граф в виде матрицы смежности. Найдем минимальный элемент. Он равен 3 3 3
- 64. Задача 1 Вычеркнем 2-ю и 3-ю строки таблицы. А столбцы 2 и 3 выделим. Найдем минимальный
- 65. Задача 1 Вычеркнем 5-ю строку таблицы. А столбец 5 выделим. Найдем минимальный элемент в выделенных столбцах.
- 66. Задача 1 Вычеркнем 1-ю строку таблицы. А столбец 1 выделим. Найдем минимальный элемент в выделенных столбцах.
- 67. Задача 1 Вычеркнем 4-ю строку таблицы. А столбец 4 выделим.
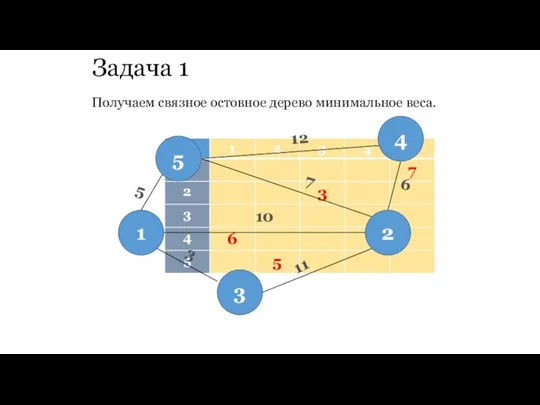
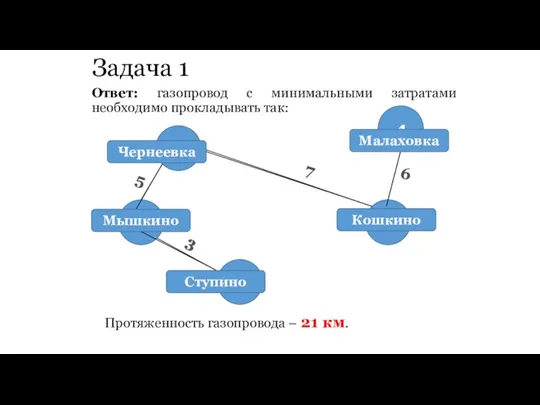
- 68. Задача 1 Получаем связное остовное дерево минимальное веса. 12 7 10 11 3 6 5 5
- 69. Задача 1 Ответ: газопровод с минимальными затратами необходимо прокладывать так: Протяженность газопровода – 21 км.
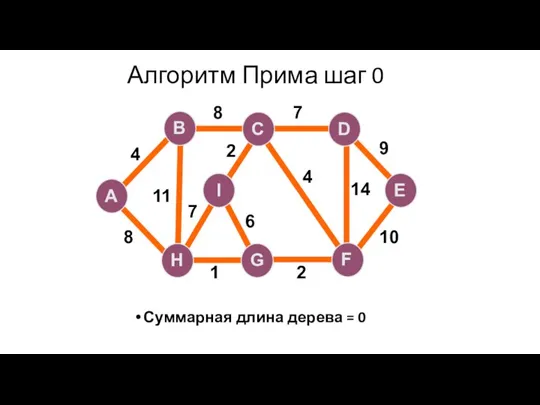
- 70. Алгоритм Прима шаг 0 Суммарная длина дерева = 0 A H G I B F C
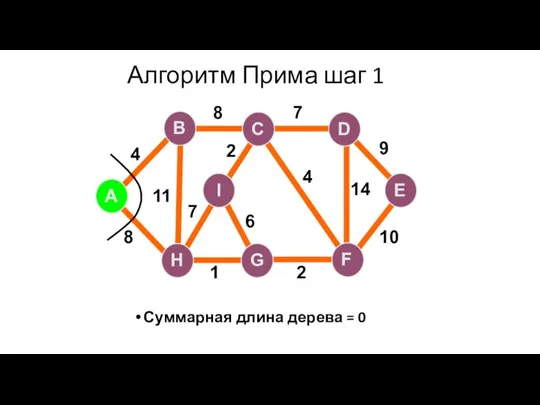
- 71. Алгоритм Прима шаг 1 Суммарная длина дерева = 0 A H G I B F C
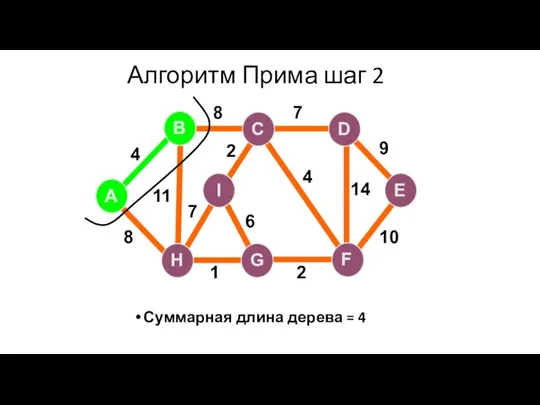
- 72. Алгоритм Прима шаг 2 Суммарная длина дерева = 4 A H G I B F C
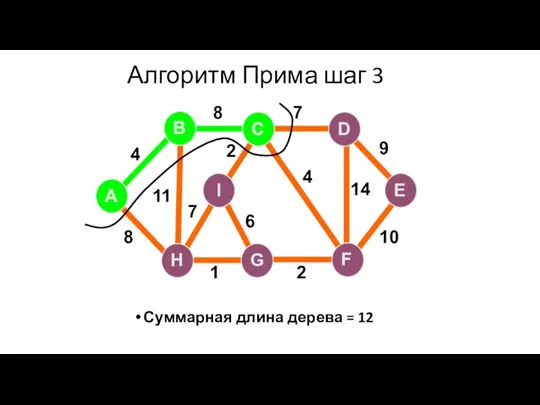
- 73. Алгоритм Прима шаг 3 Суммарная длина дерева = 12 A H G I B F C
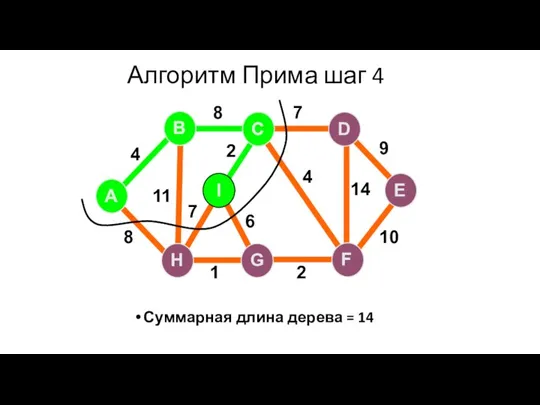
- 74. Алгоритм Прима шаг 4 Суммарная длина дерева = 14 A H G I B F C
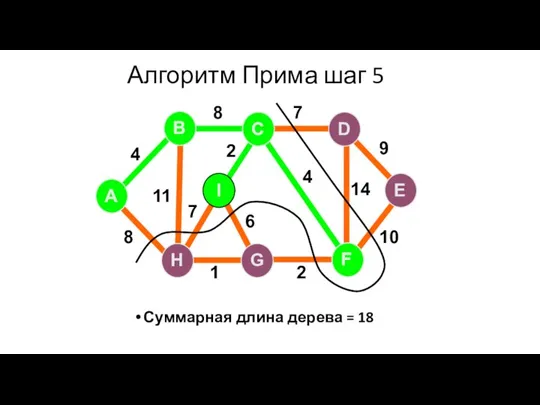
- 75. Алгоритм Прима шаг 5 Суммарная длина дерева = 18 A H G I B F C
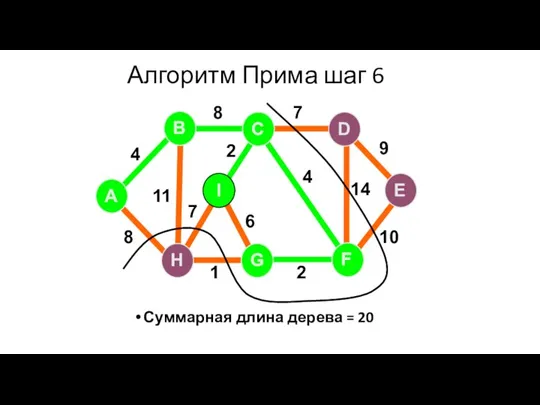
- 76. Алгоритм Прима шаг 6 Суммарная длина дерева = 20 A H G I B F C
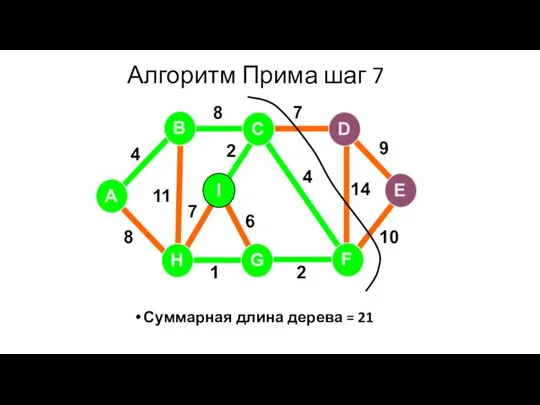
- 77. Алгоритм Прима шаг 7 Суммарная длина дерева = 21 A H G I B F C
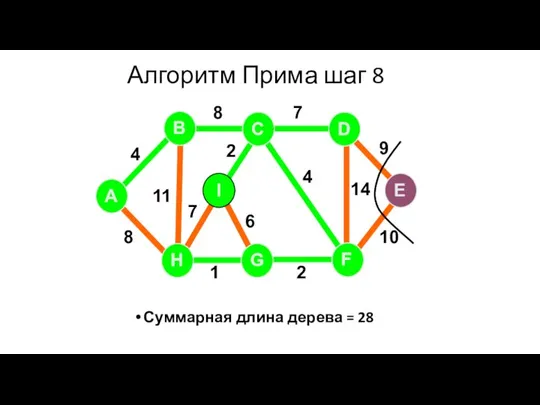
- 78. Алгоритм Прима шаг 8 Суммарная длина дерева = 28 A H G I B F C
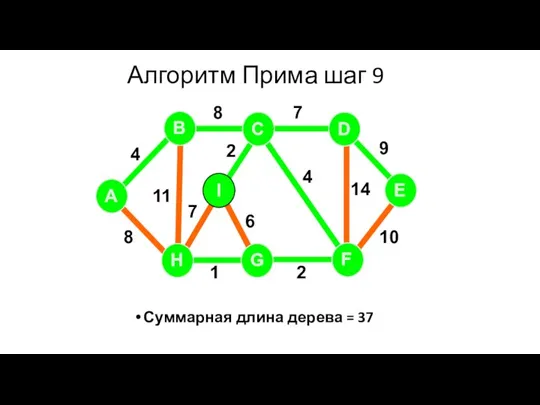
- 79. Алгоритм Прима шаг 9 Суммарная длина дерева = 37 A H G I B F C
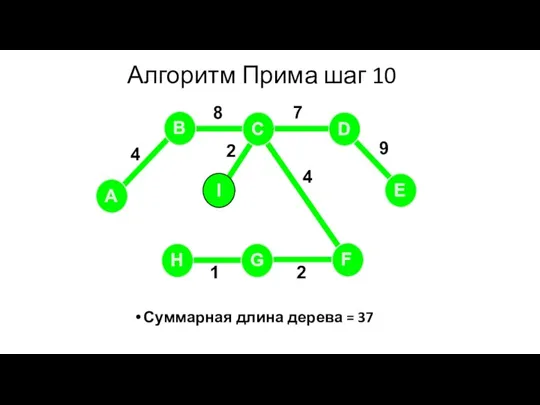
- 80. Алгоритм Прима шаг 10 Суммарная длина дерева = 37 A H G I B F C
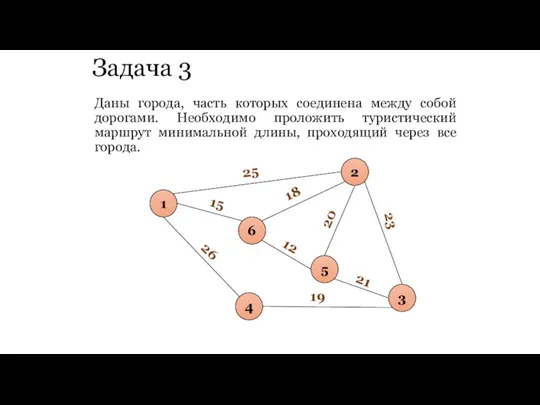
- 81. Задача 3 Даны города, часть которых соединена между собой дорогами. Необходимо проложить туристический маршрут минимальной длины,
- 82. Задача 3 Задача сводится к построению остовного связного дерева минимального веса. Рассчитаем цикломатическое число. m (количество
- 83. Алгоритм Крускала Удалить все ребра и получить остовной подграф с изолированными вершинами. Отсортировать ребра по возрастанию.
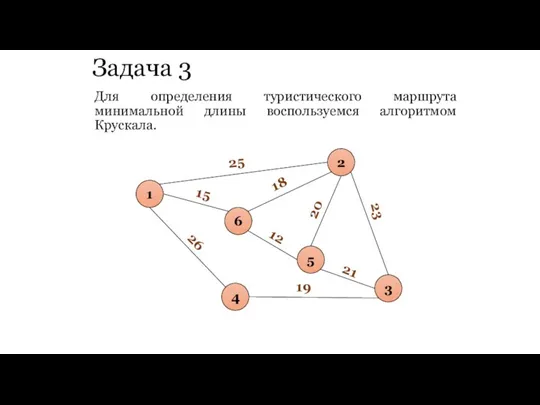
- 84. Задача 3 Для определения туристического маршрута минимальной длины воспользуемся алгоритмом Крускала.
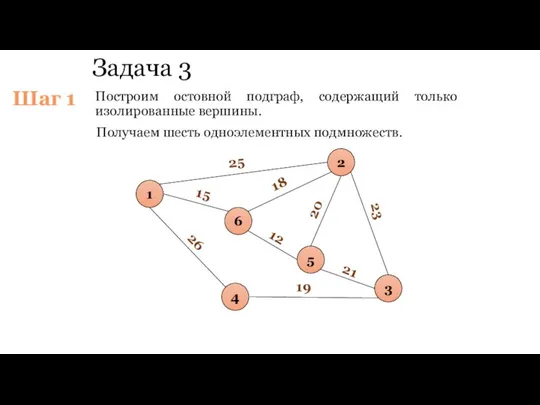
- 85. Задача 3 Построим остовной подграф, содержащий только изолированные вершины. 1 6 5 2 3 4 25
- 86. Задача 3 Найдем ребро минимального веса и добавим его в остовной подграф. 1 6 5 2
- 87. Задача 3 Среди оставшихся ребер найдем ребро минимального веса и добавим его в остовной подграф. 1
- 88. Задача 3 Среди оставшихся ребер найдем ребро минимального веса и добавим его в остовной подграф. 1
- 89. Задача 3 Среди оставшихся ребер найдем ребро минимального веса и добавим его в остовной подграф. 1
- 90. Но обе вершины принадлежат одному подмножеству {V5,V6,V1,V2}. Значит это ребро исключаем. Задача 3 Среди оставшихся ребер
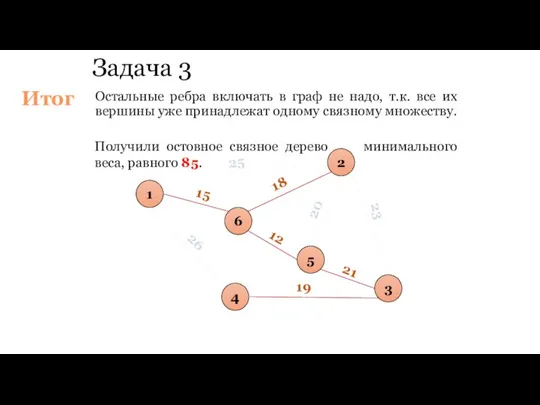
- 91. Задача 3 Остальные ребра включать в граф не надо, т.к. все их вершины уже принадлежат одному
- 92. Пример 4
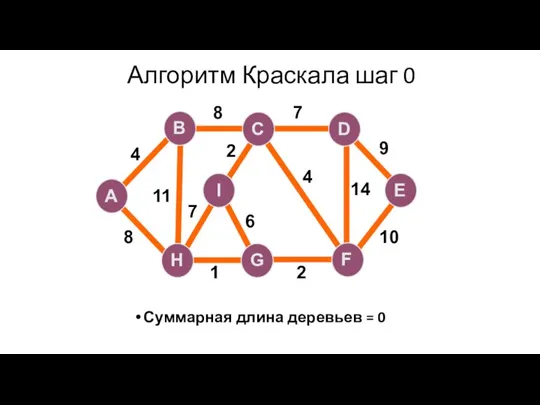
- 93. Алгоритм Краскала шаг 0 Суммарная длина деревьев = 0 A H G I B F C
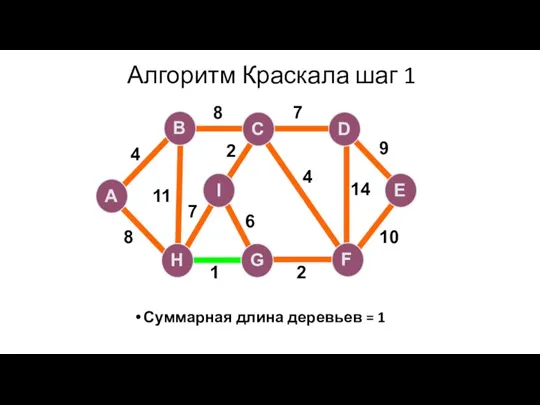
- 94. Алгоритм Краскала шаг 1 Суммарная длина деревьев = 1 A H G I B F C
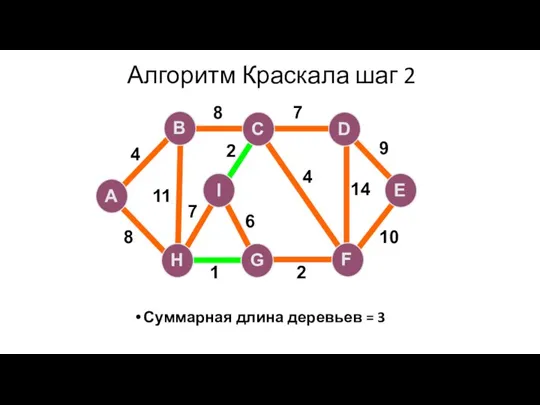
- 95. Алгоритм Краскала шаг 2 Суммарная длина деревьев = 3 A H G I B F C
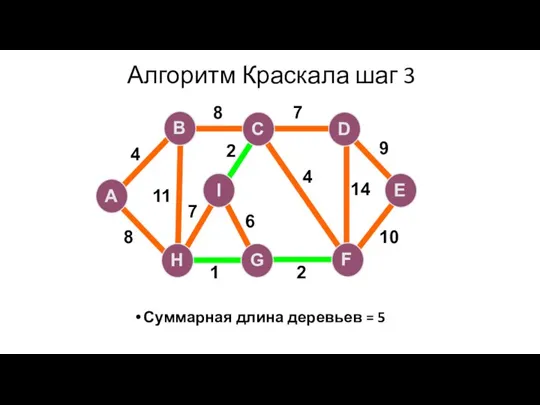
- 96. Алгоритм Краскала шаг 3 Суммарная длина деревьев = 5 A H G I B F C
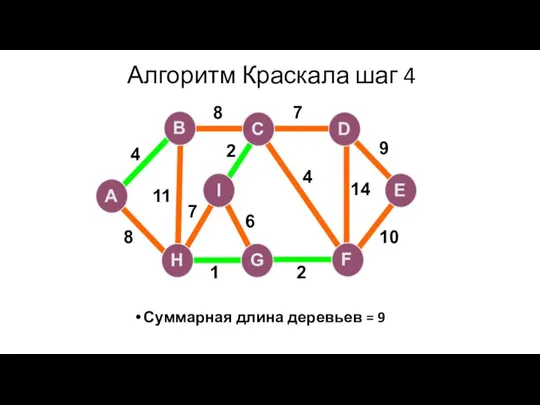
- 97. Алгоритм Краскала шаг 4 Суммарная длина деревьев = 9 A H G I B F C
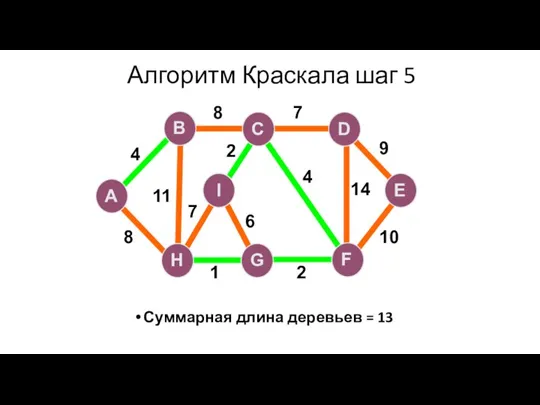
- 98. Алгоритм Краскала шаг 5 Суммарная длина деревьев = 13 A H G I B F C
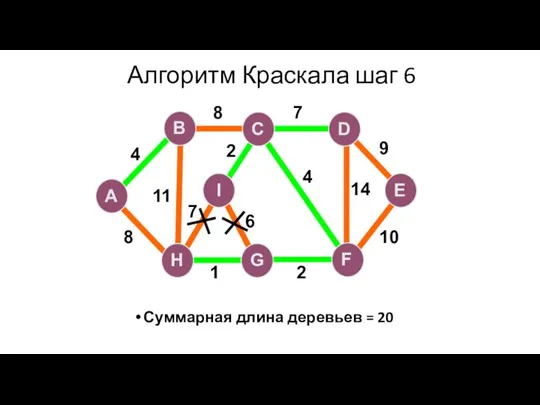
- 99. Алгоритм Краскала шаг 6 Суммарная длина деревьев = 20 A H G I B F C
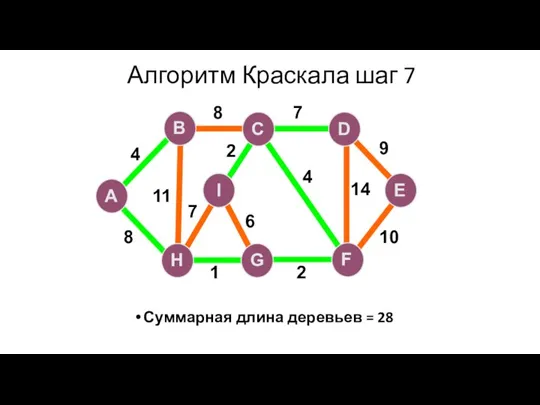
- 100. Алгоритм Краскала шаг 7 Суммарная длина деревьев = 28 A H G I B F C
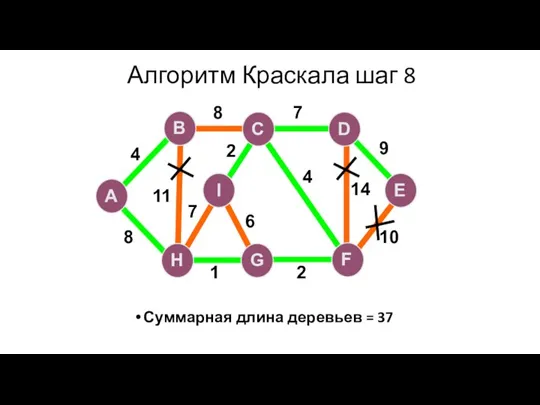
- 101. Алгоритм Краскала шаг 8 Суммарная длина деревьев = 37 A H G I B F C
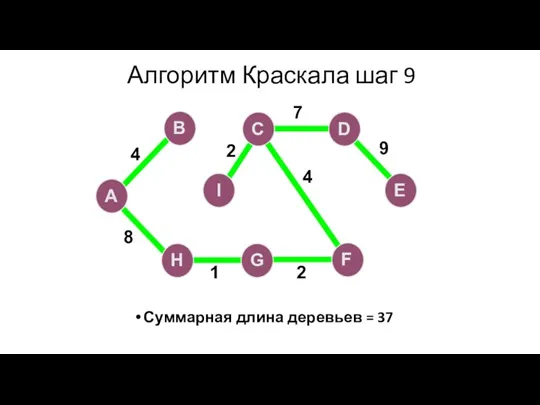
- 102. Алгоритм Краскала шаг 9 Суммарная длина деревьев = 37 A H G I B F C
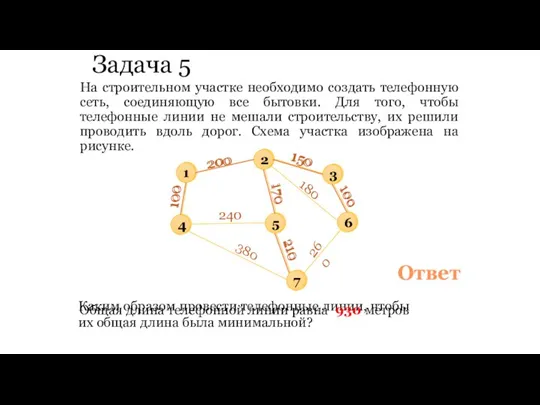
- 103. Задача 5 На строительном участке необходимо создать телефонную сеть, соединяющую все бытовки. Для того, чтобы телефонные
- 105. Скачать презентацию











































 Философия Общая характеристика предмета
Философия Общая характеристика предмета Программа Microsoft PowerPoint
Программа Microsoft PowerPoint Цветущие дворики села. Фотовыставка
Цветущие дворики села. Фотовыставка Источники трудового права
Источники трудового права Социальная защита несовершеннолетних в РФ
Социальная защита несовершеннолетних в РФ Выражение отношения к окружающему миру через изображение животных
Выражение отношения к окружающему миру через изображение животных Гиппиус
Гиппиус Методика проведения игровых программ: практические советы и рекомендации
Методика проведения игровых программ: практические советы и рекомендации Презентация1
Презентация1 Мировая религия Буддизм 7 класс
Мировая религия Буддизм 7 класс Османская империя в XIV-XVI веках
Османская империя в XIV-XVI веках Открытое акционерное общество «Сибвзрывкомплект»
Открытое акционерное общество «Сибвзрывкомплект» SQA DAYS 9:Опыт создания своей QA компании
SQA DAYS 9:Опыт создания своей QA компании БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Выпускная работа по«Основам информационных технологий» Минск – 2010 г.
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Выпускная работа по«Основам информационных технологий» Минск – 2010 г. НИР-2008
НИР-2008 Речевые ошибки
Речевые ошибки Силикатная промышленность
Силикатная промышленность Криптовалюты. Блокчейн и биткойн
Криптовалюты. Блокчейн и биткойн Отчет о проделанной работе ЮАО. Бизнес разведка Тайм кафе
Отчет о проделанной работе ЮАО. Бизнес разведка Тайм кафе 1 класс
1 класс Бизнес-план антикафе Час за минуту
Бизнес-план антикафе Час за минуту ГК РФ Статья 87. Основные положения об обществе с ограниченной ответственностью
ГК РФ Статья 87. Основные положения об обществе с ограниченной ответственностью Повторение
Повторение Основы коммерческой деятельности
Основы коммерческой деятельности Алкоголь
Алкоголь Жизненный цикл проекта. Инициация
Жизненный цикл проекта. Инициация Потестарно-политические институты обских угров в дореволюционной России и в советское время (Никифорова И.М.)
Потестарно-политические институты обских угров в дореволюционной России и в советское время (Никифорова И.М.) Принятие управленческих решений
Принятие управленческих решений