Американский стандарт блочного шифрования Rijndael

Второго октября 2000 года департамент торговли США подвел итоги конкурса по выработке нового стандарта шифрования США. Победителем стал алгоритм «Rijndael», разработанный бельгийскими криптографами.

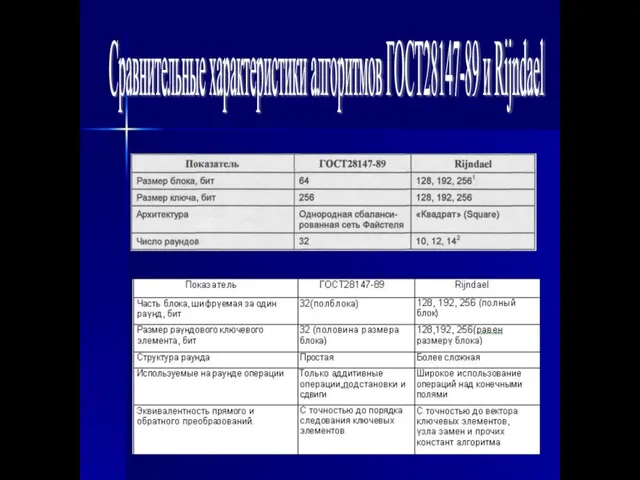
Сравнительные характеристики алгоритмов ГОСТ28147-89 и Rijndael

Сравнение общих архитектурных принципов
Криптоалгоритм ГОСТ28147-89, как и большинство шифров «первого поколения», разрабатывавшихся в 70-е годы и в первой половине 80-х, базируется на архитектуре «сбалансированная сеть Фейстеля»
Шифр Rijndael имеет архитектуру «квадрат» (Square).
Эта архитектура базируется на прямых преобразованиях шифруемого блока, который представляется в форме матрицы байтов. Зашифрование также состоит из серии однотипных шагов, раундов, однако на каждом раунде блок преобразуется как единое целое и не остается неизменных частей блока.
Таким образом, за раунд шифруется полный блок, следовательно, для обеспечения сопоставимой сложности и нелинейности преобразования таких шагов требуется вдвое меньше по сравнению с сетью Файстеля.

Сравнение общих архитектурных принципов

Общая схема алгоритма
Каждый раунд заключается в побитовом сложении по модулю 2 текущего состояния шифруемого блока и ключевого элемента раунда, за которым следует сложное нелинейное преобразование блока, сконструированное из трех более простых преобразований.
В Rijndael шифруемый блок и его промежуточные состояния в ходе преобразования представляются в виде матрицы байтов 4×n, где
n =4, 6, 8 в зависимости от размера блока.

Функция нелинейного преобразования
байтовая подстановка - каждый байт преобразуемого блока заменяется новым значением,
извлекаемым из общего для всех байтов матрицы вектора замены;
побайтовый циклический сдвиг в строках матрицы: первая строка остается неизменной, вторая строка циклически сдвигается влево на один байт, третья и четвертая строка циклически сдвигаются влево соответственно на 2 и 3 байта;
матричное умножение - полученная на предыдущем шаге матрица умножается слева на матрицу-циркулянт размера 4x4:

Сравнение раундов шифрования

Эквивалентность прямого и обратного преобразований
Шифр Rijndael построен на базе прямых преобразований. Как и для всех подобных алгоритмов, обратное преобразование строится из обращений шагов прямого преобразования, применяемых в обратном порядке.

Произведем следующие преобразования:
Операция побайтовой замены (S) коммутативна с процедурой побайтового сдвига строк матрицы:
Кроме того, согласно правилам матричной алгебры по закону ассоциативности можно также поменять порядок побитового прибавления ключа по модулю два и умножения на матрицу:

После преобразований
Алгоритмическая структура прямого и обратного преобразований идентична

Процедуры зашифрования и расшифрования различаются:
в обратном преобразовании используется вектор замен, обратный в операционном смысле вектору замен прямого преобразования;
в обратном преобразовании число байтов, на которые сдвигается каждая строка матрицы данных в операции построчного байтового сдвига другое;
в обратном преобразовании в шаге матричного умножения блок данных умножается
слева на матрицу, обратную той, что используется при прямом преобразовании;
в обратном преобразовании ключевые элементы используются в обратном порядке, и, кроме того, все элементы за исключением первого и последнего, должны быть умножены слева на матрицу М-1.

Выработка ключевых элементов
Существуют два алгоритма генерации последовательности ключевых элементов - для ключа размером 128/192 бита и для ключа размером 256 бит.
Ключ и ключевая последовательность представляются в виде векторов 4-х байтовых слов, и начальный участок последовательности заполняется словами из ключа, точно так же, как в ГОСТе. Последующие слова ключевой последовательности вырабатываются по рекуррентному соотношению группами, кратными размеру ключа.

Первое 4-байтовое слово вырабатывается с использованием сложного нелинейного преобразования, остальные - по простому линейному соотношению:
где Nk - число 32-битовых слов в ключе (4 или 6)
G(w) - нелинейное преобразование 32-битовых слов - включает байтовый сдвиг, побайтовую подстановку по вектору замен и побитовое сложение по модулю 2 с вектором, зависящим от номера вырабатываемой группы элементов:
P(i/Nk) - 4-байтовое слово, конструируемое особым образом и не зависящее от ключа.
Полученные из описанного выше потока 4-байтовые слова группируются в ключевые элементы необходимого размера, равного размеру шифруемого блока, и используются на раундах шифрования.

Выбор узлов замен и констант
При конструировании узлов замен помимо тривиальных требований обратимости и простоты описания были приняты во внимание следующие соображения:
• минимизация самой большой по величине характеристики корреляции между линейными
комбинациями входных и выходных битов (определяет устойчивость к линейному криптоанализу);
минимизация наибольшего нетривиального значения в таблице EXOR (определяет устойчивость к дифференциальному криптоанализу);
сложность алгебраического выражения, описывающего узел, в GF(28).

Операция байтовой замены
Операция байтовой замены в алгоритме Rijndael описывается следующим уравнением:
Это преобразование начинается с мультипликативной инверсии заменяемого байта в описанном выше конечном поле GF(28), - значение 00 при этом меняется на самого себя, затем результат подвергается аффинному преобразованию.
Полиномы этого преобразования выбраны таким образом, чтобы у итогового отображения отсутствовали точки неподвижности (S(X)=X) и «антинеподвижности»
(S(X) = ~X). Здесь знаком «~» обозначена операция побитового инвертирования.