Архитектура ЭВМ. Логические основы ЭВМ

Логические основы ЭВМ
Базовые функциональные элементы ЭВМ (вентили)
Основные логические схемы

Вентили
Логический элемент - электронное устройство, на входах и выходах которого сигнал может иметь только один из двух дискретных уровней напряжения: низкий (0–2V) или высокий (3–5V).
Базовым считают элемент с наиболее простой структурой, на основе которого легче всего создавать другие электронные схемы.
И, ИЛИ, НЕ
И-НЕ

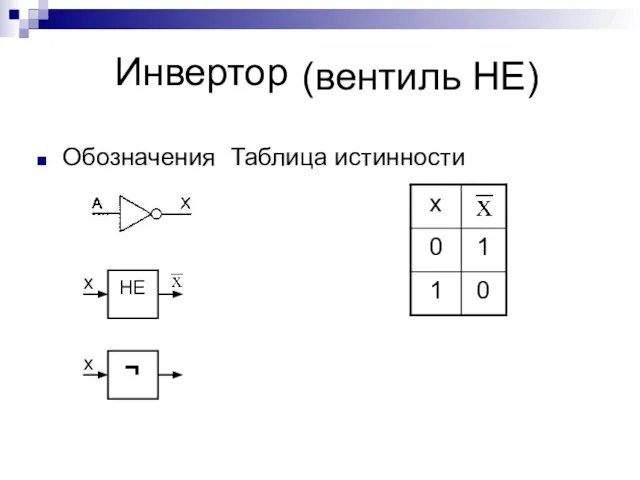
Инвертор
Обозначения Таблица истинности
(вентиль НЕ)

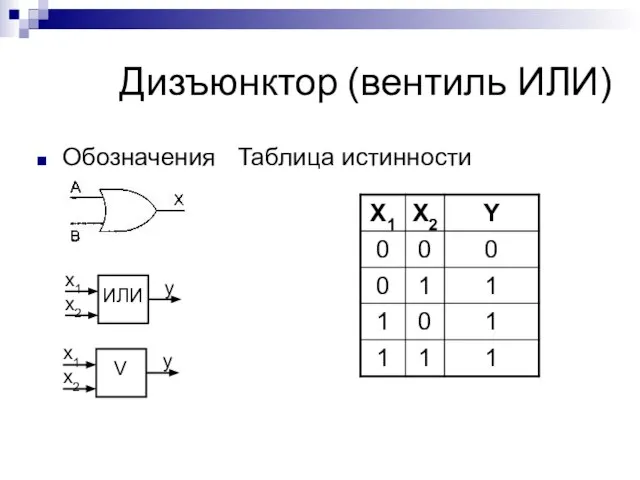
Дизъюнктор
Обозначения Таблица истинности
(вентиль ИЛИ)

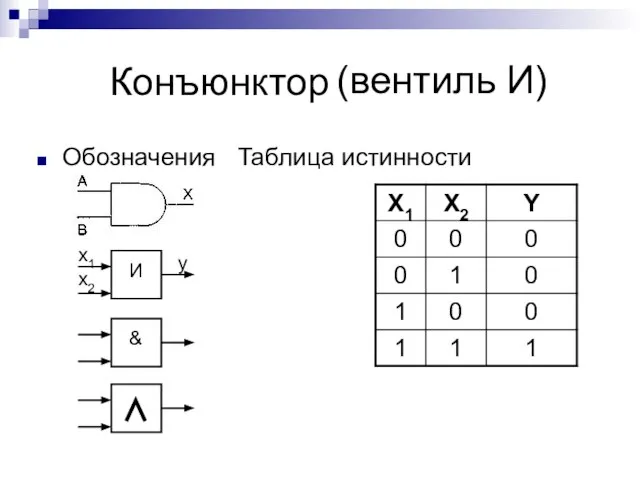
Конъюнктор
Обозначения Таблица истинности
(вентиль И)

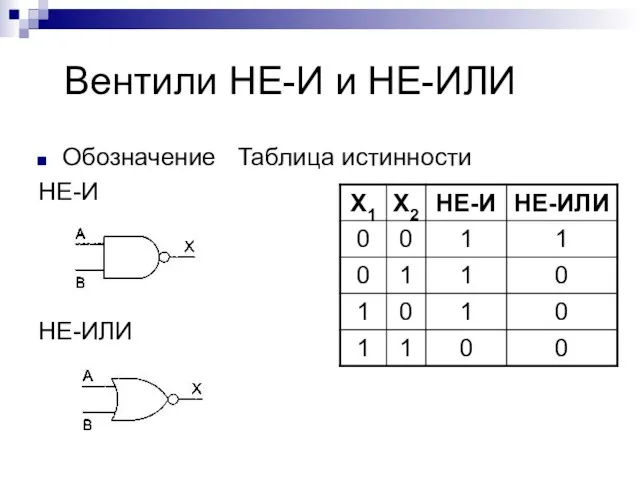
Вентили НЕ-И и НЕ-ИЛИ
Обозначение Таблица истинности
НЕ-И
НЕ-ИЛИ

Уровень физических устройств
Транзистор имеет три соединения с внешним миром: коллектор, базу и эмиттер.
Если входное напряжение Vin низкое, то транзистор выключается и действует как очень большое сопротивление. Это приводит к выходному сигналу Vout, близкому к Vcc (обычно +5В).
Если Vin высокое, то транзистор включается и действует как провод, вызывая заземление сигнала Vout (по соглашению 0 В).
На переключение с одного состояние на другое обычно требуется несколько наносекунд.

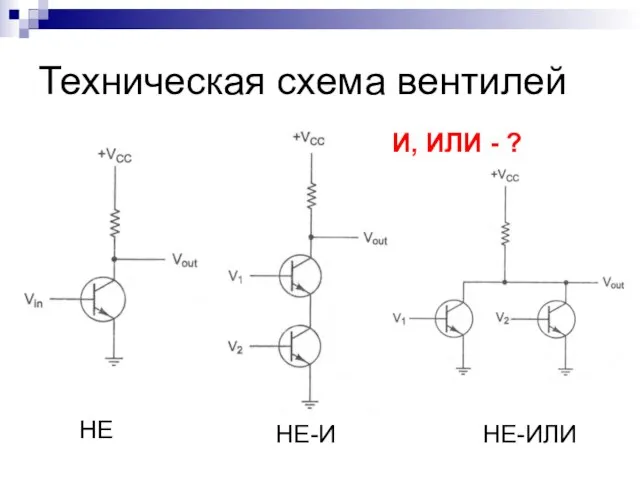
Техническая схема вентилей
НЕ
И, ИЛИ - ?
НЕ-И
НЕ-ИЛИ

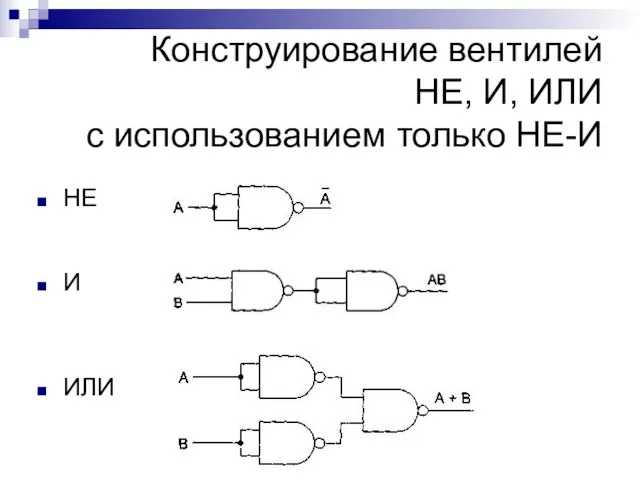
Конструирование вентилей
НЕ, И, ИЛИ
с использованием только НЕ-И
НЕ
И
ИЛИ

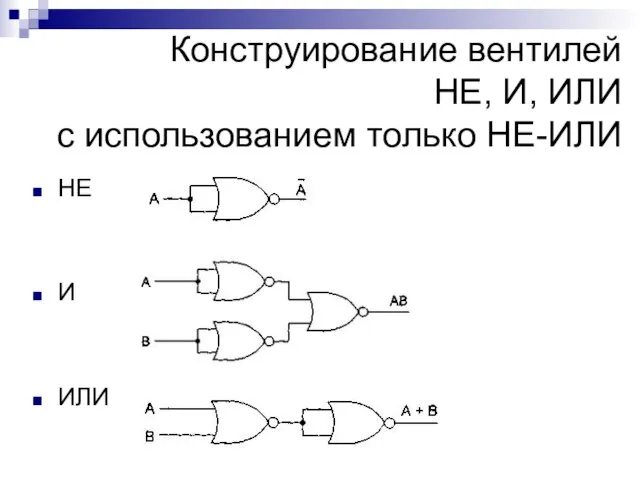
Конструирование вентилей
НЕ, И, ИЛИ
с использованием только НЕ-ИЛИ
НЕ
И
ИЛИ

Логический синтез схем
Одноразрядный двоичный полусумматор
Полный одноразрядный сумматор
Полный многоразрядный сумматор
Дешифратор
Триггер

Как реализовать схему
Составить таблицу истинности для данной функции
Обеспечить инверторы, чтобы порождать инверсии для каждого входного сигнала.
Нарисовать вентиль И для каждой строки таблицы истинности с результатом 1.
Соединить вентили И с соответствующими входными сигналами.
Вывести выходы всех вентилей И в вентиль ИЛИ.

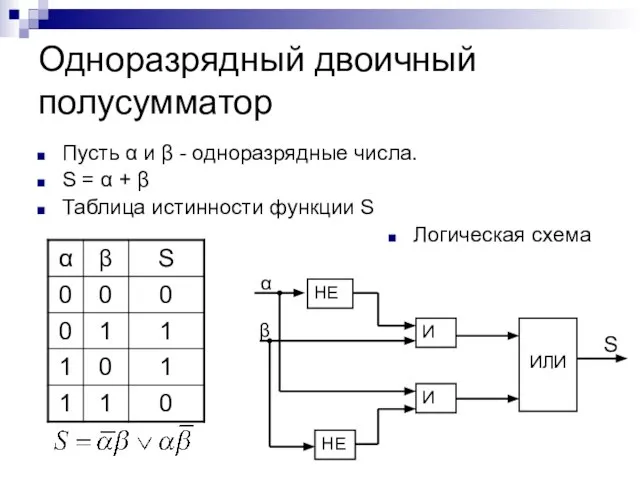
Одноразрядный двоичный полусумматор
Пусть α и β - одноразрядные числа.
S = α + β
Таблица истинности функции S
Логическая схема
НЕ
НЕ
α
β
И
И
ИЛИ
S

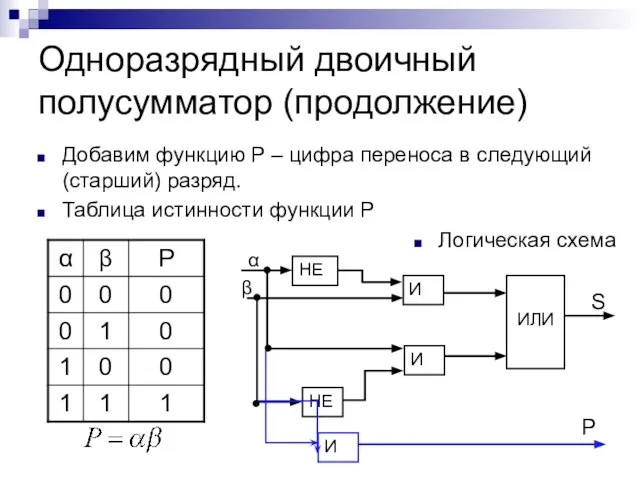
Одноразрядный двоичный полусумматор (продолжение)
Добавим функцию P – цифра переноса в следующий (старший) разряд.
Таблица истинности функции Р
Логическая схема
НЕ
НЕ
α
β
И
И
ИЛИ
S
Р
И

Полный одноразрядный сумматор
— полусумматор, дополненный третьим входом – значением разряда переноса из соседнего младшего разряда.
Таблица истинности

Полный многоразрядный сумматор
β1
0
P2
S1
Σ
α1
β2
p2
P3
S2
Σ
α2
βn
pn
Pn+1
Sn
Σ
αn
…
- линия переполнения
α = (αnαn-1… α2α1) β = (βnβn-1… β2β1)

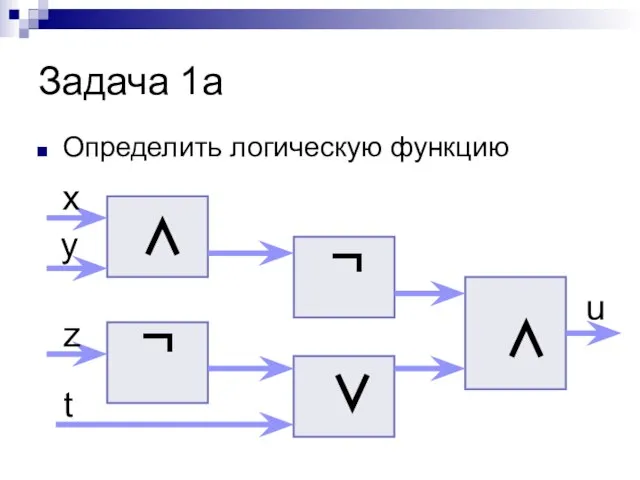
Задача 1а
Определить логическую функцию

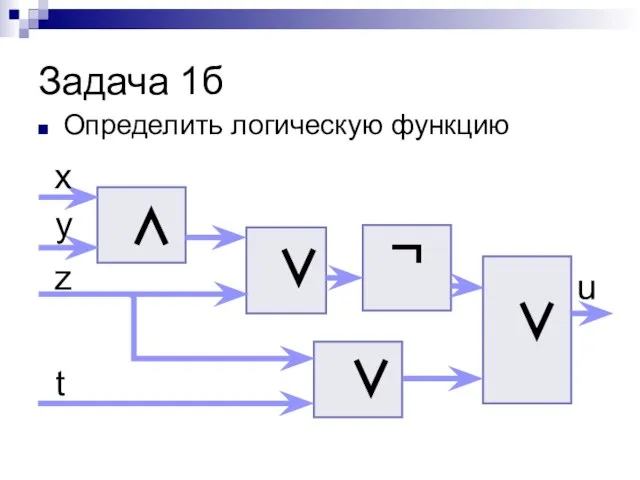
Задача 1б
Определить логическую функцию
∧

Задача 2
Построить логическую схему для функции:
а)
б)

Задача 2в
Построить наиболее экономную схему для функции

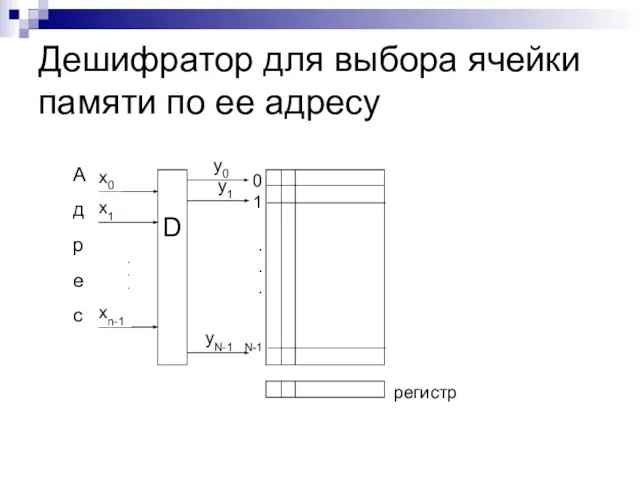
Дешифратор
Д. – схема, имеющая n входов и 2n выходов. Входные сигналы образуют двоичное число, определяющее номер выходного сигнала,
который устанавливается в 1. Значения остальных выходных сигналов должны быть установлены в 0.

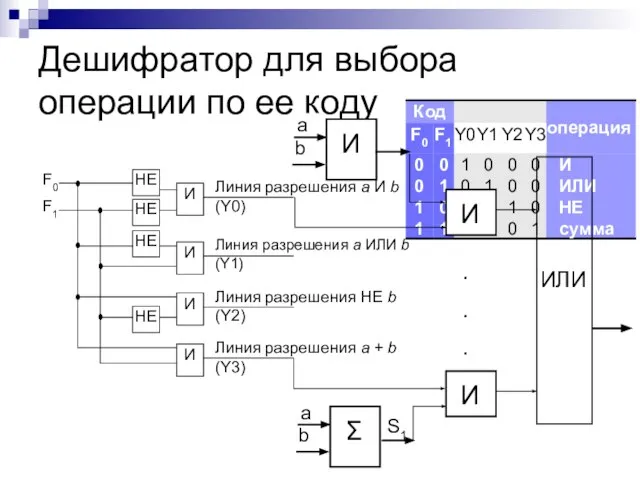
Дешифратор для выбора операции по ее коду
b
S1
Σ
a
И
b
И
a
И
ИЛИ
.
.
.

Дешифратор для выбора ячейки памяти по ее адресу

Определения
Схема называется комбинационной (схема без памяти), если значения переменных на выходе схемы однозначно зависят только от значения входных переменных.
Схема называется последовательностной (схема с памятью), если значения выходов схемы зависят не только от значений на входах, но и от внутреннего состояния (внутренних переменных).
Ч.С.
Схема называется схемой с обратными связями, если в качестве внутренних переменных используются значения выходных переменных, полученных в предыдущий момент времени.

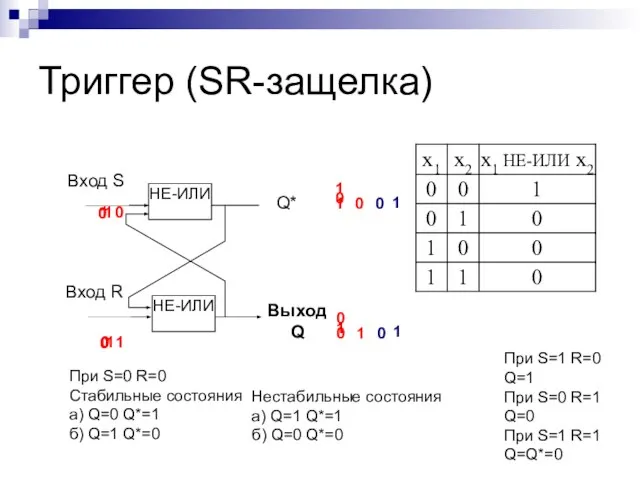
Триггер (SR-защелка)
1
0
0
0
0
1
0
0
1
1
1
0
0
1
0
1
1
0
1
1
При S=0 R=0
Стабильные состояния
a) Q=0 Q*=1
б) Q=1 Q*=0
Нестабильные состояния
a) Q=1 Q*=1
б) Q=0 Q*=0
При S=1 R=0
Q=1
При S=0 R=1
Q=0
При S=1 R=1
Q=Q*=0