Арифметические основы организации компьютера

Понятие о системах счисления
Компьютер – это электронное цифровое устройство.
Электронное устройство потому, что внутри компьютера любая информация передается, хранится, обрабатывается и выводится только через изменение состояния электронов.
Цифровое устройство потому, что любая информация представляется с помощью чисел.
Для того чтобы записывать числа, нужно использовать какую-нибудь систему счисления. Система счисления показывает, по каким правилам мы запи-сываем числа и выполняем над ними действия (сложение, умножение и т.п.).
Обычно мы используем десятичную систему счисления. В этой системе любое число записывается с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Количество цифр в системе счисления называется ее основанием. Основание десятичной системы равно 10. Десятичная система возникла потому, что в древности люди использовали для счета десять пальцев на двух руках.
из 27

Двоичная система счисления
На компьютере для записи чисел используется двоичная система счисления. В этой системе всего две цифры: 0 и 1, основание системы равно 2.
Двоичная система для компьютера выбрана не случайно. Дело в том, что вводимая информация проходит в компьютере в виде изменения состояния электронов. Эти изменения либо есть, либо их нет. Удобно отсутствию изменения сопоставить цифру нуль (0), а наличию – цифру один (1).
Для примера приведем соответствие первых пятнадцати чисел десятичной системы числам двоичной системы счисления (даны на след. слайде).
В проблематике компьютерной арифметики основной интерес вызывают два вопроса – способ представления чисел в двоичной системе счисления и алгоритмы выполнения над ними четырех базовых арифметических операций (сложения, вычитания, умножения и деления). Это относится как к целым числам, так и к вещественным.
из 27

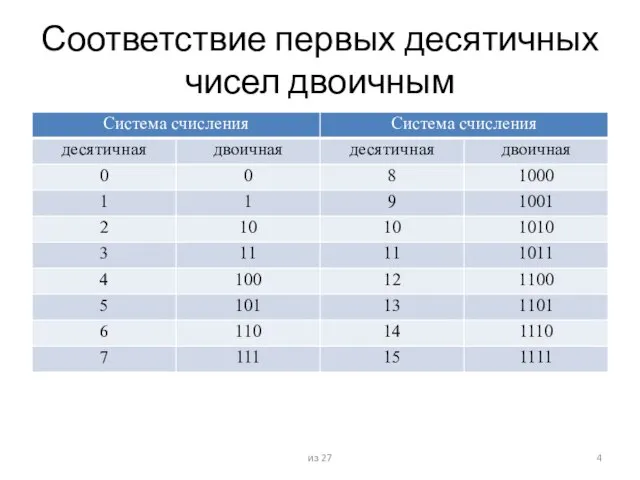
Соответствие первых десятичных чисел двоичным
из 27

Позиционность 10-й и 2-й систем
В десятичной системе позиция цифры в числе означает количество единиц, десяток, сотен и т.д.
Например, число 4728 означает:
4728 = 4*1000+7*100+2*10 +8 или 4728 = 4*103 + 7*102 + 2*101 +8*100.
Можно сказать, что цифры числа (разряды) нумеруются справа налево, причем счет идет с нуля. В данном примере 8 – нулевой разряд,
2 – первый, 7 – второй, 4 – третий.
По такому же принципу представляются и величины, имеющие дробную часть: 472.83 = = 4*102 + 7*101 + 2*100 +8*10–1 +3*10–2.
В двоичной также используется позиционная система: 102 = 1*21 + 0*20 = 210 ; 112 = 1*21 + 1*20 = 310 ; 1002 =1*22 +0*21 + 0*20 = 410.
При представлении дробной части числа используются отрицательные степени двойки: 1001,1012 = 23 + 20 + 2–1 + 2–3 = 9,62510.
из 27

Преобразование из 10-й в 2-ю (целые числа)
Целая и дробная части представления преобразуются раздельно.
Целую часть последовательно делим на 2 и выписываем остатки в обратном порядке. Это и даст нам двоичное представление числа.
Таким образом, 1110 = 10112.
из 27

Преобразование из 10-й в 2-ю (дробные числа)
Процедура преобразования дробей представляет собой последовательное умножение на 2.
На каждом шаге дробная часть предыдущего произведения вновь умножается на 2, а цифры, представляющие целую часть произведений (они всегда равны либо 0, либо 1), выписываются как последовательные (слева направо) цифры двоичного представления.
Таким образом, 0.8110 = 0.1100112 (приблизительно).
Видим, что процедура перевода дробей не всегда дает точный результат. В данном случае оборвали на шестой цифре (разряде).
из 27

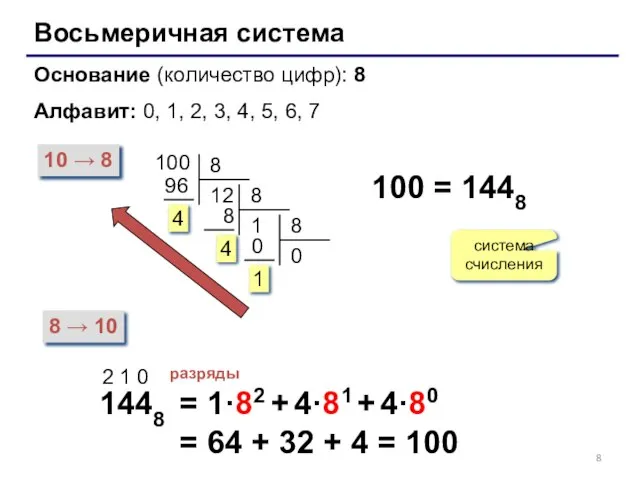
Восьмеричная система
Основание (количество цифр): 8
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
10 → 8
8 → 10
100
100 = 1448
система счисления
1448
2 1 0
разряды
= 1·82 + 4·81 + 4·80
= 64 + 32 + 4 = 100

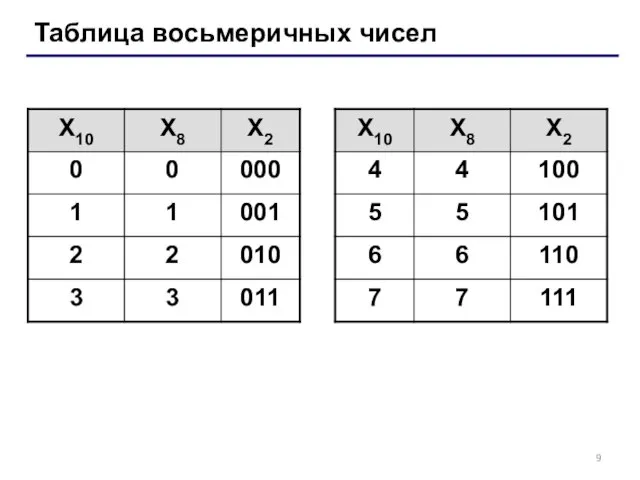
Таблица восьмеричных чисел

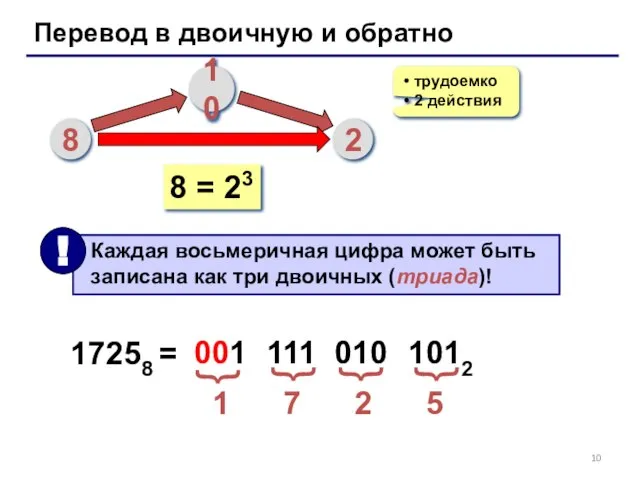
Перевод в двоичную и обратно
8
10
2
трудоемко
2 действия
8 = 23
17258 =
1 7 2 5
001
111
010
1012
{
{
{
{

Перевод из двоичной системы
10010111011112
Шаг 1. Разбить на триады, начиная справа:
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной восьмеричной цифрой:
1
3
5
7
Ответ: 10010111011112 = 113578
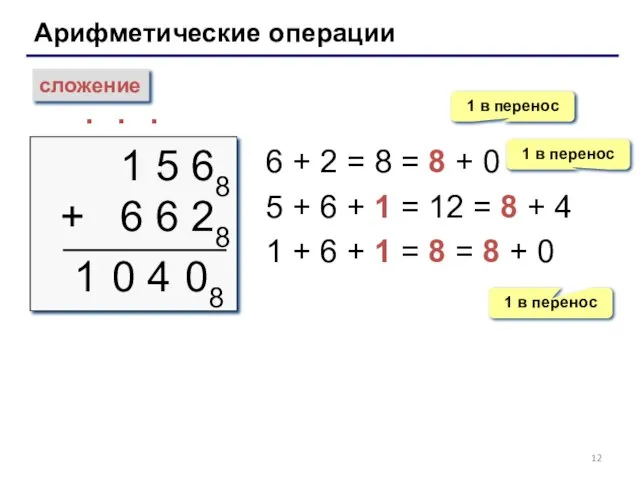
001 001 011 101 1112
1

Арифметические операции
сложение
1 5 68
+ 6 6 28
∙
1
6 + 2 = 8 = 8 + 0
5 + 6 + 1 = 12 = 8 + 4
1 + 6 + 1 = 8 = 8 + 0
∙
1 в перенос
1 в перенос
∙
08
0
4
1 в перенос

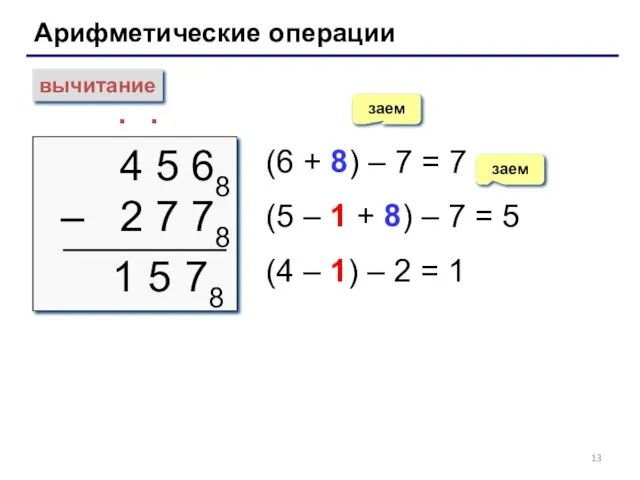
Арифметические операции
вычитание
4 5 68
– 2 7 78
∙
(6 + 8) – 7 = 7
(5 – 1 + 8) – 7 = 5
(4 – 1) – 2 = 1
∙
заем
78
1
5
заем

16-ричная система счисления
Поскольку современная электронно-вычислительная техника принципиально построена на двоичных элементах, любые данные в ней представляются только двоичными кодами.
Но пользователю применять начертание кода в виде длинных последовательностей нулей и единиц очень неудобно.
Поэтому специалисты используют для работы с двоичными кодами «на бумаге» более компактное их представление. Такую компактную форму дает шестнадцатеричная система
Для преобразования из двоичного представления в 16-ричное двоичные цифры группируются по четыре (как говорят, разбивают на тетрады), и каждая четырехзначная комбинация заменяется шестнадцатеричной цифрой (см. след слайд).
из 27

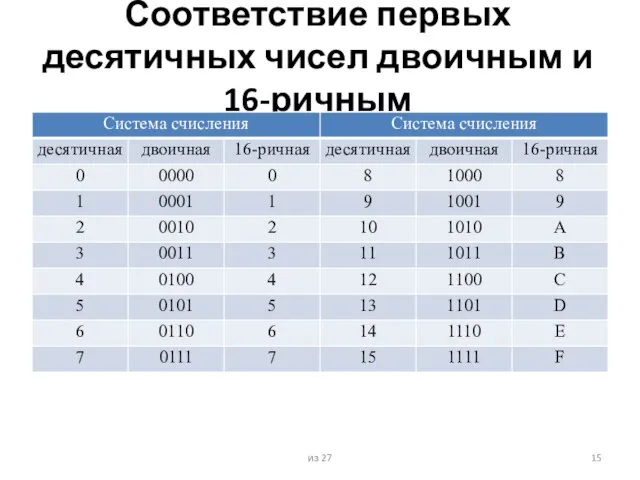
Соответствие первых десятичных чисел двоичным и 16-ричным
из 27

Преобразование из 2-й в 16-ю (целые числа)
Разбиение целой части двоичного числа на тетрады идет справа налево (и впере-ди, если необходимо, дополняют крайнюю тетраду до четырех цифр нулями).
Дробную же часть разбивают на тетрады слева направо (и также, если необходимо, в конце дописывают нули).
Например, как известно, 25510 = 111111112. Здесь имеем две тетрады: 1111 1111. Значит, 25510 = 111111112 = FF16. Проверим правильность – переведем в десятичную систему из 16-ричной: FF16 = F*161 + F*160 = 15*16 + 15*1 = 240 + 15 = 25510, т.е. все верно.
Другой пример: 10 1111 1000 0101 1001. Видно, что впереди необходимо добавить два нуля: 0010 1111 1000 0101 1001.
Тогда имеем: 2 F 8 5 9
Проверим, пересчитав в 10-й системе: 10 1111 1000 0101 10012 = 217+215+214+213+212+211+26+24 +23+1=19464910.
2F85916 = 2*164 + F*163 + 8*162 + 5*161 + 9 = 2*65536 +15*4096 +8*256 +89 = 19464910.
из 27

Преобразование из 2-й в 16-ю (дробные числа)
Рассмотрим пример числа с дробной частью: 10011110001,11001100001.
Здесь необходимо приписать нуль впереди целой части и нуль позади дробной части (для получения тетрад): 0100 1111 0001,1100 1100 0010.
В результате имеем 4F1, CC216.
Проверка: 4*16^2 + 15*16^1+1*16^0 + 12*16^-1 + 12*16^-2 + 2*16^-3 = 1024 + 240 + 1 + 0.75 + 0.046875 + 0.000488281 = 1265.797363
А из 2-й: 2^10 + 2^7+2^6+2^5+2^4+2^0+2^-1+2^-2+2^-5+2^-6+2^-11 = 1265.79736328125
Ясно, что перевести целое число из 10-й системы в 16-ричную можно также последовательным делением десятичного числа на 16 и выписыванием остатков в обратном порядке (уже в 16-ричном виде).
Дробь же переводится последовательным умножением на 16 и выписыванием целых частей произведений в правильном порядке (т.е. все так же, как и для двоичных чисел)
из 27

Арифметические операции в 2-й системе счисления
Существует несколько соглашений о едином формате представления как положительных, так и отрицательных чисел. Всех их объединяет то, что старший разряд (самый левый) является знаковым разрядом (0 – это плюс, 1 – это минус). Все последующие биты слова составляют значащие разряды числа.
Простейшим форматом, который использует знаковый разряд, является прямой код. Например, при 8-разрядном представлении:
+18 = 00010010, –18 = 10010010
Однако прямой код неудобен при использовании в вычислениях. Во-первых, сложение и вычитание положительных и отрицательных чисел выполняются по-разному, а потому требуется анализировать знаковые разряды операндов (слагаемых). Во-вторых, в прямом коде числу 0 соответствует две комбинации: +0 = 00000000, –0 = 10000000.
По этой причине вместо него применяют так называемый дополнительный код.
из 27

Обратный код
В обратном, как и в прямом коде, старший разряд отводится для представления знака числа, но остальные разряды интерпретируются в зависимости от того, положительное число или отрицательное.
Обратный код положительного числа остается неизменным. А обратный код отрицательного двоичного числа формируется дополнением модуля исходного числа нулями до самого старшего разряда модуля, а затем поразрядной заменой всех нулей числа на единицу и всех единиц на нули. В знаковом разряде обратного кода у положительных чисел будет 0, а у отрицательных будет 1. В общем случае обратный код является дополнением модуля исходного числа до наибольшего числа без знака, помещенного в разрядную сетку.
Например, при 8-разрядном представлении числа +2810 имеем:
+2810 = 000111002.
Если же возьмем –2810, то в обратном коде имеем:
–2810 = 111000112.
из 27

Дополнительный код
Однако на основе обратного кода строится так называемый дополнительный код, который позволяет существенно облегчить арифметические операции над числами с разными знаками.
Дополнительный код строится следующим образом. Сначала формируется обратный код, а затем к младшему разряду добавляют 1. При выполнении арифметических операций положительные числа представляются в прямом коде, а отрицательные числа – в дополнительном.
Например, –510 преобразуем в дополнительный код: 5 в двоичном виде дает (при 4-разрядном двоичном представлении) 0101, тогда –5 даст 1101 (впереди 1 – знак «минус»). Получаем обратный код: 1010, затем добавляем в младший разряд единицу: 1011 – это и есть дополнительный код –5. Итак, –510 = 10112.
из 27

Дополнительный код (много разрядов)
Иногда нужно записать число с большим числом разрядов. Если число представлено в прямом коде, то достаточно перенести знаковый разряд в крайний левый бит нового представления числа, а остальные дополнительные биты заполнить нулями. Например,
+18 в прямом коде на 8 разрядов 00010010;
+18 в прямом коде на 16 разрядов 00000000 00010010;
–18 в прямом коде на 8 разрядов 10010010;
–18 в прямом коде на 16 разрядов 10000000 00010010.
Но с отрицательными числами в дополнительном коде такая схема не дает правильного результата. Преобразование дополнительного кода при расширении разрядной сетки выполняется следующим образом: нужно скопировать значение знакового разряда во все дополнительные биты. Если исходное число было положительным, то все дополнительные биты заполнятся нулями, а если отрицательным – единицами.
Эта операция называется расширением знака. Применим это правило к тому же примеру:
+18 в дополнительном коде на 8 разрядов 00010010;
+18 в дополнительном коде на 16 разрядов 00000000 00010010;
–18 в дополнительном коде на 8 разрядов 11101110;
–18 в дополнительном коде на 16 разрядов 11111111 11101110.
из 27

Арифметические операции с целыми числами (сложение и вычитание)
Рассмотрим эти операции на примерах. Числа будем рассматривать как представляемые в 16-разрядной сетке (см. след. слайд)
При выполнении сложения чисел с одинаковыми знаками результат может оказаться таким, что не вмещается в используемую разрядную сетку, т.е. получается число, которое выходит за диапазон представления – происходит переполнение. В этом случае на схему АЛУ возлагается функция выявить переполнение и выработать сигнал, который должен воспрепятствовать использованию в дальнейшем полученного ошибочного результата. Существует следующее правило обнаружения переполнения.
Если знаки слагаемых совпадают, то переполнение возникает в том и только в том случае, когда знак суммы, полученной по правилам сложения в дополнительном коде, отличается от знака слагаемых.
При вычитании нужно вычитаемое число рассматривать как отрицательное и далее складывать уменьшаемое и вычитаемое в дополнительном коде
из 27

Сложение в дополнительном коде
из 27

Сложение в дополнительном коде (продолжение)
В двух случаях (пятом и шестом) ограниченная разрядность чисел приводит к искажению не только величины, но и знака результата. Исправить положение можно, добавляя к результату (случай 5) или вычитая (случай 6) число 216 = 65536.
из 27

Арифметические операции с вещественными числами
Любое вещественное число N, представляемое в системе счисления с основанием p, можно представить в виде N = ± M ∙ p±k, где М – мантисса; k – порядок числа (целое число).
Например, десятичное число 234,47 можно представить следующим образом: 234,47 = 0,23447* 103
А, скажем, двоичное число 1011, 01 запишется так: 1011,01 = 0,101101*24 = 0,101101*10100.
Здесь мы учли, что 210 = 102 и 410 = 1002
Такое представление чисел называется представлением с плавающей точкой, где порядок определяет, на сколько порядков необходимо осуществить сдвиг относительно запятой.
Когда плавающая запятая размещена в мантиссе перед первой значащей цифрой (как в нашем случае записано в правой части: 0,23447* 103 или 0,101101*10100), то такая форма записи называется нормализованной.
из 27

Смещенный код
В компьютере для работы с порядками чисел используется смещенный код. Суть его в том, что если на порядок отводится разрядная сетка в n разрядов, то смещенный порядок 2n–1 + p. Например, если для порядка отводится 8 разрядов, то 2n–1 = 128. Порядок при n = 8 будет принимать значения от –128 до 128. В итоге значения порядка в смещенном коде будут от 0 до 255. Это позволяет работать с порядками как с целыми без знака.
Вещественные числа в компьютере представляются в таком виде (см. след. слайд)
Здесь m – задает точность представления мантиссы. Например, если на вещественное число отводится четыре байта (или 32 разряда), то имеем формат так называемого короткого вещественного. При этом на мантиссу отводятся разряды с 0-го по 22-й, смещенный порядок занимает с 23-го по 30-й разряд, а в 31-м (крайнем левом разряде) будет знак мантиссы (т.е. знак всего числа). Условились, что знак задается так: 1 (в 31-разряде) для отрицательных чисел и 0 – для положительных.
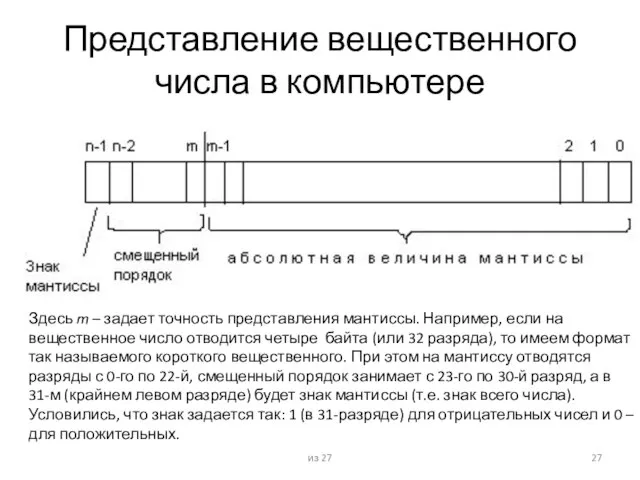
из 27

Представление вещественного числа в компьютере
Здесь m – задает точность представления мантиссы. Например, если на вещественное число отводится четыре байта (или 32 разряда), то имеем формат так называемого короткого вещественного. При этом на мантиссу отводятся разряды с 0-го по 22-й, смещенный порядок занимает с 23-го по 30-й разряд, а в 31-м (крайнем левом разряде) будет знак мантиссы (т.е. знак всего числа). Условились, что знак задается так: 1 (в 31-разряде) для отрицательных чисел и 0 – для положительных.
из 27

Правило сложения (вычитания)
При алгебраическом сложении и вычитании чисел, представленных в формате с плавающей точкой, сначала уравниваются порядки слагаемых.
В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков.
В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются.
В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата вправо. При каждом сдвиге вправо порядок результата увеличивается на единицу.
Операцию вычитания сведем к сложению с отрицательным числом. Напомним, что отрицательные числа представляются в дополнительном коде.
из 27

Пример. Представить в форме с плавающей точкой числа A = –314,15, B = 27,18 и выполнить операцию A+B
Переведем эти числа в двоичную систему счисления (целая часть переводится методом деления на 2, дробная – методом умножения на 2):
A = – 100111010,00100110011001*2^0 = – 0,10011101000100110011001*2^9.
B = 11011,001011100001010001*2^0 = 0,11011001011100001010001*2^5.
Смещенный порядок числа A будет равен P*A = PA + N = 9 + 128 =13710 =
= 1000 10012. Смещенный порядок числа B будет равен P*B = PB + N = 5+128 =
=13310 = 1000 01012.
Запишем числа в заданном формате:
A: 1.10001001. 10011101000100110011001;
B: 0.10000101. 10000001110000101000111.
Для выполнения операции сложения необходимо выровнять порядки чисел, т.е. принять порядок меньшего числа (B) равным порядку большего числа (A), уменьшив мантиссу меньшего числа путем сдвига вправо на число разрядов, равное разности порядков чисел (PA – PB =4) :
B: 0.10001001.000010000001110000101000111.
из 27

Пример… (продолжение)
Мантиссу отрицательного числа MB представляем в дополнительном коде, положительного MA – в прямом. Тогда
MA = 1.01100010111011001100111
+
MB = 0.00001101100101110000101
MA + MB =1.01110000100000111101100.
Результат отрицательный (в знаковом разряде стоит единица), мантисса нормализованная. Запишем результат с учетом порядка в разрядной сетке заданного формата:
A+B : 1.10001001. 01110000100000111101100.
Учтем, что т.к. результат отрицательный, то мантисса записана в дополнительном коде. Преобразуем из дополнительного в прямой (вычтем единицу и инвертируем цифры):
MA + MB = – 0.10001111011111000010100.
из 27

Пример… (окончание)
Проверка:
Рассчитаем порядок. 10001001 = 27 +23 + 20 = 128 +8 + 1 = 13710.
Или с учетом смещения 137 – 128 = 9.
Тогда, т.к. мантисса имеет вид: – 0.10001111011111000010100, то с учетом порядка имеем: 100011110.11111000010100 (сдвинули десятичную точку на 9 позиций).
Значит, целая часть результата:
2^8 + 2^4 + 2^3 + 2^2 + 2^1 =256+16+8+4+2 = 286.
Дробная часть результата:
2^–1 +2^–2 + 2^–3 + 2^–4 + 2^–5 = 0,96875 ≅ 0,97.
Эти же числа сложим в десятичной системе:
–314,15+ 27,18 = –286,97, т.е. все верно.
из 27

Индивидуальное домашнее задание № 1
Пора приступать к выполнению ИДЗ №1
Пример задания:
В итоге следует оформить отчет и сдать!
из 27
Задание 1. Перевести числа из двоичной системы в десятичную.
Задание 2 Перевести числа из 16-ричной системы в десятичную.
Задание 3 Перевести числа из десятичной системы в двоичную.
Задание 4. Перевести числа из десятичной системы в 16-ричную.
Задание 5. Перевести числа из двоичной системы в шестнадцатиричную.
При выполнении заданий 3–5 следует проводить проверку с исполь-зованием десятичной системы счисления.
Вариант Задание 1 Задание 2 Задание 3 Задание 4 Задание 5
1 110101001012 6A516 170110 1701,170110 11010100101,001012
2 110010000102 64216 160210 1602,160210 11001000010,001012