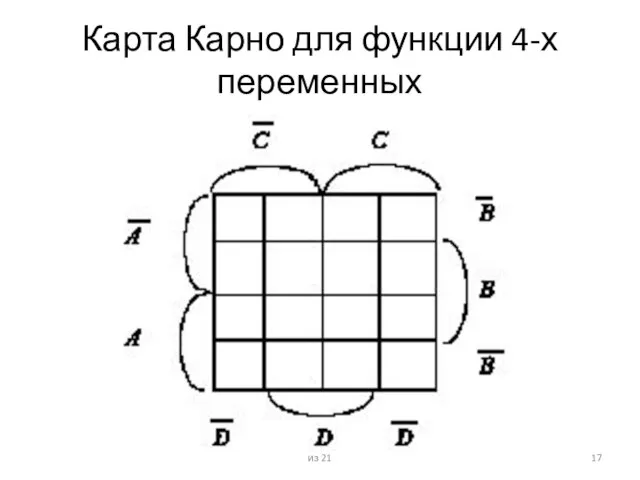
переменных (теоретически – не более шести, а практически – четырех).
Карта для задания функции, зависящей от n переменных, это таблица из 2n клеток, в которых представлены значения функции для всех возможных комбинаций значений переменных
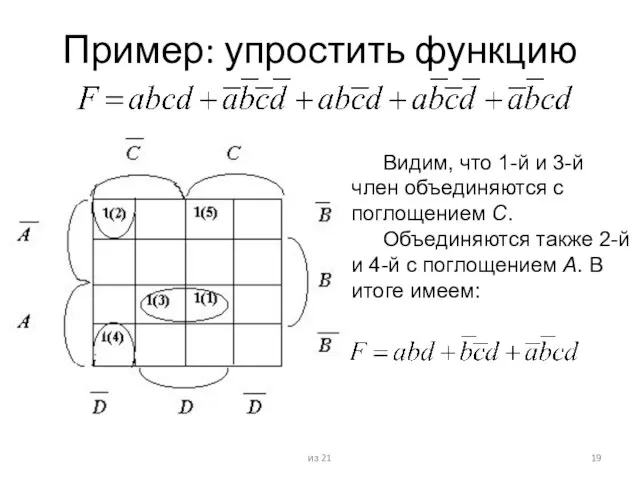
Булева функция представляется в карте Карно следующим образом. Каждая клетка, в которой проставлено значение 1, соответствует определенному конъюнктивному члену в ДНФ функции. В этот конъюнктивный член входят переменные, имеющие значение 1 в комбинации для этой клетки, и инверсии переменных, имеющих в комбинации для этой клетки значение 0
Если необходимо заполнить карту для функции, заданной некоторым булевым выражением, то сначала это выражение нужно привести к канонической форме, т.е. к форме, в каждом члене которой будут присутствовать все переменные, а уже затем приступить к заполнению клеток карты Карно
из 21











 Функциональная структура системы управления проектной деятельностью в Правительстве РФ
Функциональная структура системы управления проектной деятельностью в Правительстве РФ 10/4/991 Company Confidential 1 Системы Agilent Technologies для анализа покрытия и качества обслуживания в системах сотовой связи.
10/4/991 Company Confidential 1 Системы Agilent Technologies для анализа покрытия и качества обслуживания в системах сотовой связи. АМПУТАЦИИ И ЭКЗАРТИКУЛЯЦИИ конечностей
АМПУТАЦИИ И ЭКЗАРТИКУЛЯЦИИ конечностей  Пригласительный билет
Пригласительный билет Фотосинтез особенности метаболизма
Фотосинтез особенности метаболизма Тютчев Фёдор Иванович
Тютчев Фёдор Иванович 20220929_Konstruktionsrückmeldungen_Slawa
20220929_Konstruktionsrückmeldungen_Slawa Что делать? Что сделать?
Что делать? Что сделать? Жестокое обращение с детьми
Жестокое обращение с детьми Отчёт по практике
Отчёт по практике Урок - конференция
Урок - конференция Моя семья. Исследовательский проект (2 класс)
Моя семья. Исследовательский проект (2 класс) Договоры. Обязательство
Договоры. Обязательство Промышленность особенности структуры и территориальной организации
Промышленность особенности структуры и территориальной организации Подбор ИТ специалистов: практика и еще раз практика
Подбор ИТ специалистов: практика и еще раз практика Экспорт пищевых лесных ресурсов Беларуси
Экспорт пищевых лесных ресурсов Беларуси Первый интернет-портал для детей и подростков
Первый интернет-портал для детей и подростков Государство - это организация политической власти,
Государство - это организация политической власти, Герои Чернушки
Герои Чернушки Инвестиционный проект по строительству цеха по производству топливного этанола
Инвестиционный проект по строительству цеха по производству топливного этанола Позволить уйти
Позволить уйти Travelling and Transport
Travelling and Transport Sporty extremalne
Sporty extremalne Современный урок русского языка
Современный урок русского языка Тема: Коллектив и его воспитательный потенциал.
Тема: Коллектив и его воспитательный потенциал. Презентация на тему пожары и взрывы презентация по обж 8 класс
Презентация на тему пожары и взрывы презентация по обж 8 класс  Вторая мировая Алтайский край
Вторая мировая Алтайский край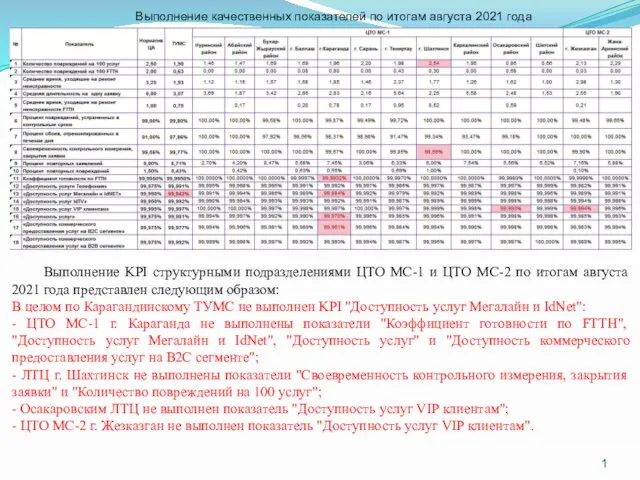 Выполнение качественных показателей по итогам августа 2021 года
Выполнение качественных показателей по итогам августа 2021 года