Содержание
- 2. Асимптоты функции Определение: Асимптотой функции называется прямая линия, к которой приближается значение функции по мере удаления
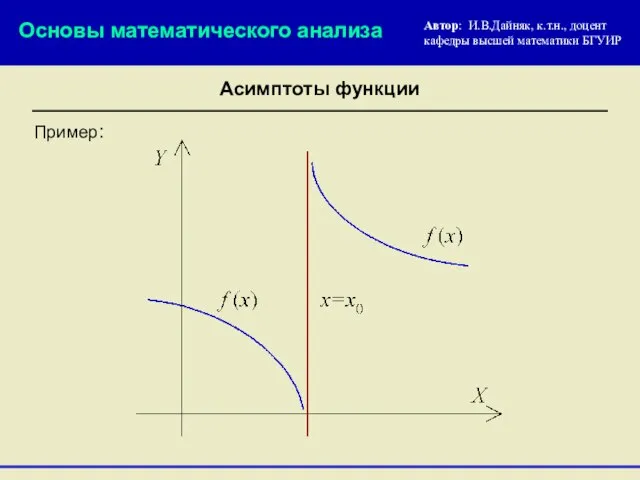
- 3. Асимптоты функции Вертикальная асимптота: или Прямая х = х0 называется вертикальной асимптотой графика функции f (x),
- 4. Автор: И.В.Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Асимптоты функции Пример: Основы математического анализа
- 5. Пример 1: Решение: Автор: И.В.Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Найти вертикальные асимптоты функции Ответ:
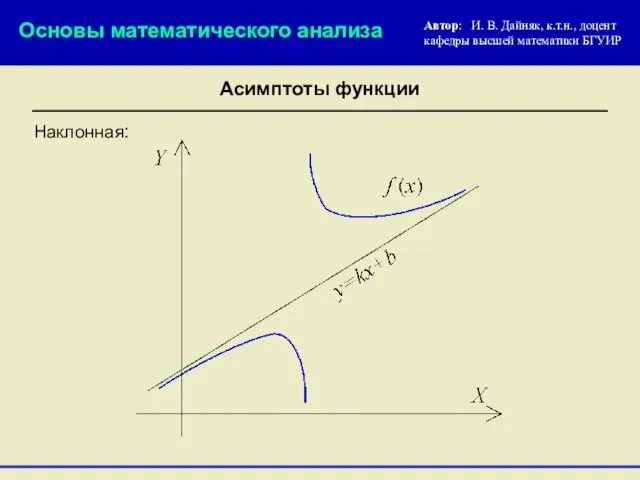
- 6. Наклонная асимптота: или графика функции f (x), если при Прямая y = k x + b
- 7. Наклонная: Основы математического анализа Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Асимптоты функции
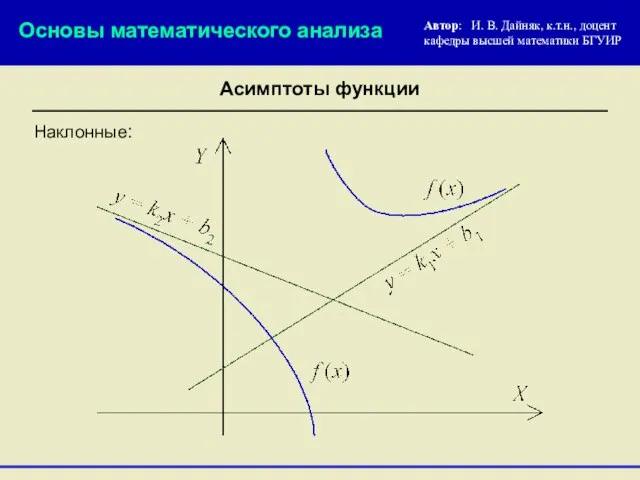
- 8. Наклонные: Основы математического анализа Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Асимптоты функции
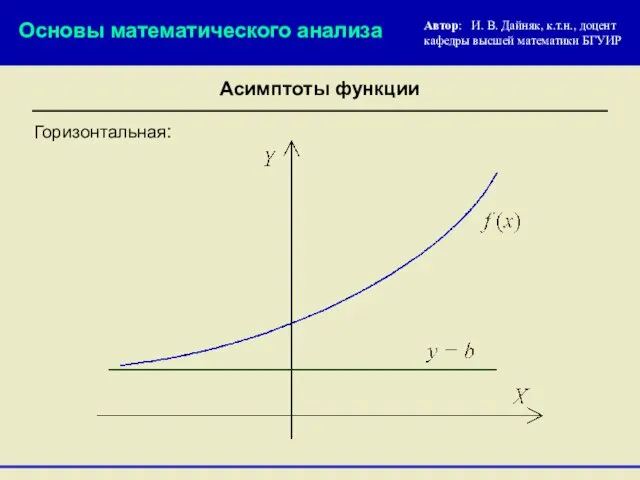
- 9. Горизонтальная: Основы математического анализа Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Асимптоты функции
- 10. Теорема: Для того чтобы прямая y = k x + b являлась наклонной асимптотой графика функции
- 11. Пример 2: Решение: Найти наклонные асимптоты функции Ответ: Асимптоты функции Основы математического анализа Автор: И. В.
- 12. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ Лекция 7 Основы математического анализа Автор: И. В. Дайняк, к.т.н., доцент кафедры
- 13. Непрерывность функции в точке Определение 1: Функция f (x) называется непрерывной в точке х0, если она
- 14. Непрерывность функции в точке Определение 2: Функция f (x) называется непрерывной в точке х0, если она
- 15. Непрерывность функции в точке Определение 3: Функция f (x) называется непрерывной в точке х0, если её
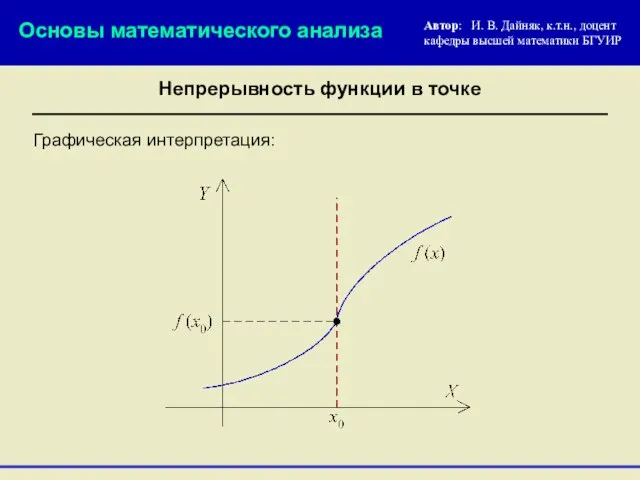
- 16. Графическая интерпретация: Основы математического анализа Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР Непрерывность
- 17. Пример 3: Решение: Установить непрерывность или разрывность функции Ответ: Основы математического анализа Автор: И. В. Дайняк,
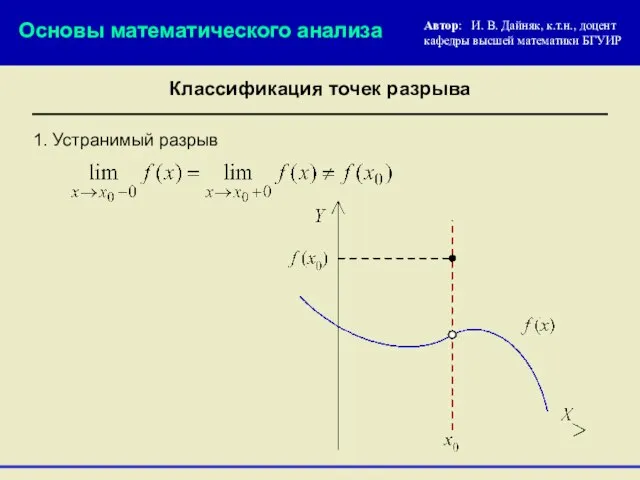
- 18. 1. Устранимый разрыв Основы математического анализа Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР
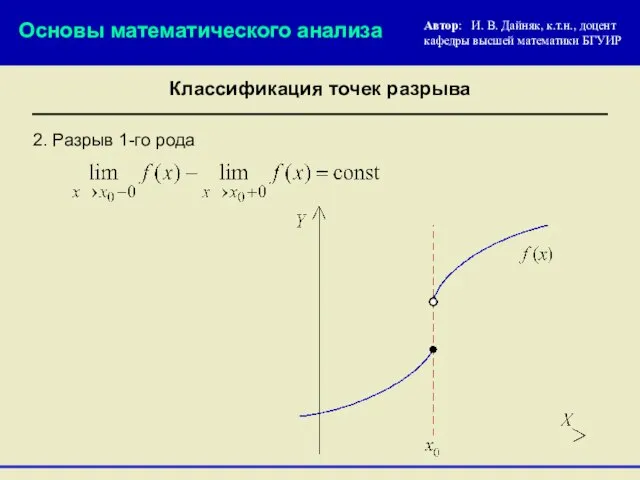
- 19. 2. Разрыв 1-го рода Основы математического анализа Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики
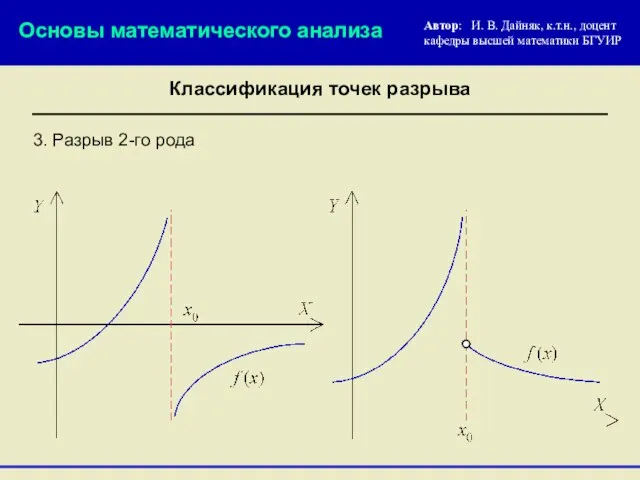
- 20. 3. Разрыв 2-го рода Основы математического анализа Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики
- 21. Пример 4: Решение: Найти точки разрыва функции и установить их характер Ответ: Основы математического анализа Автор:
- 23. Скачать презентацию












 ДЕПАРТАМЕНТ образования ГОРОДА МОСКВЫМОСКОВСКИЙ ГОРОДСКОЙ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
ДЕПАРТАМЕНТ образования ГОРОДА МОСКВЫМОСКОВСКИЙ ГОРОДСКОЙ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ Святая Екатерина Александрийская
Святая Екатерина Александрийская Summer memory game
Summer memory game Defining Culture
Defining Culture RPM 89. Образовательная сессия
RPM 89. Образовательная сессия Экосистема леса Лесные кустарники и травы
Экосистема леса Лесные кустарники и травы Спостереження за моїм собакою
Спостереження за моїм собакою Предприятие ООО «Квантсервер» известно на рынке Алтайского края и других регионов России как ведущий поставщик кукурузных палоче
Предприятие ООО «Квантсервер» известно на рынке Алтайского края и других регионов России как ведущий поставщик кукурузных палоче 2. Сущность права
2. Сущность права Презентация на тему Характеристика стран НИС
Презентация на тему Характеристика стран НИС  Общая физическая подготовка. Развитие всех физических качеств (сила, выносливость, координации, скорость, ловкость, гибкость)
Общая физическая подготовка. Развитие всех физических качеств (сила, выносливость, координации, скорость, ловкость, гибкость)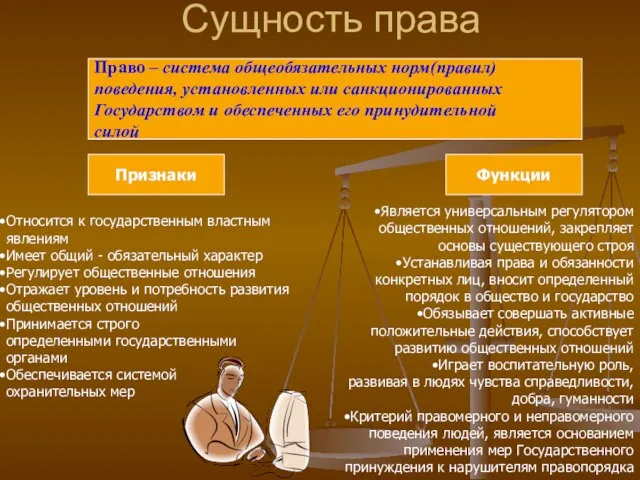 Сущность права
Сущность права Школьникам о правильном питании
Школьникам о правильном питании Лягушачье золото
Лягушачье золото НА ПРОСТОРАХ
НА ПРОСТОРАХ Стихотворения М.Ю.Лермонтова «Три пальмы», «Листок», «Утёс»
Стихотворения М.Ю.Лермонтова «Три пальмы», «Листок», «Утёс» Презентацияпо темеОтдел Папоротникообразные.
Презентацияпо темеОтдел Папоротникообразные. NEW YORK CITY
NEW YORK CITY  Герб
Герб Презентация к интеллектуальной игре «Конституция – главный арбитр государства»(по Конституции 1993г.) Подготовила: Варюхина Римм
Презентация к интеллектуальной игре «Конституция – главный арбитр государства»(по Конституции 1993г.) Подготовила: Варюхина Римм Вашему вниманию предлагается новая система в MainLink «Быстрый старт», которая позволяет запустить продвижение сайта по одному или бо
Вашему вниманию предлагается новая система в MainLink «Быстрый старт», которая позволяет запустить продвижение сайта по одному или бо О полезных ископаемых и первых железных дорогах
О полезных ископаемых и первых железных дорогах полная и краткая форма
полная и краткая форма Напольный светильник "Семейный очаг"
Напольный светильник "Семейный очаг" С масленицей. Готовка блинов
С масленицей. Готовка блинов Возвращение блудного сына Рембрандта
Возвращение блудного сына Рембрандта История Российского Флага
История Российского Флага Волшебные ленты
Волшебные ленты