Содержание
- 2. Задачи большого вызова (Kenneth G. Wilson, Cornell University, 1987) Вычислительная газовая динамика: Создание летательных аппаратов, эффективных
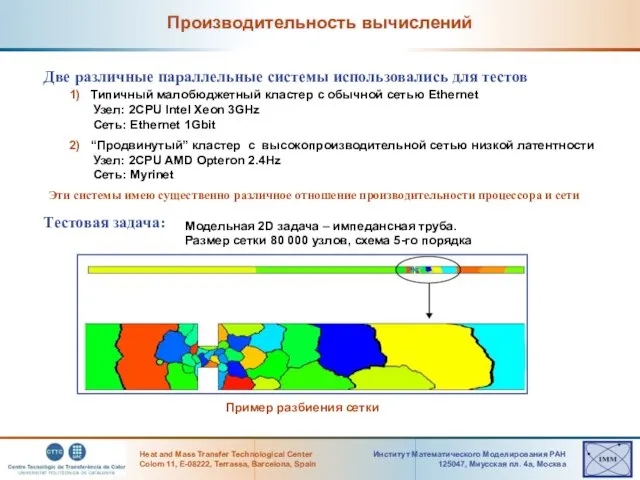
- 3. Дозвуковая аэродинамическая труба Т-104, ЦАГИ Скорость потока 10–120 м/с Диаметр сопла 7 м Длина рабочей части
- 8. Суперкомпьютеры Не просто составляют конкуренцию натурному эксперименту, но: Необходимы для его проведения Позволяют делать то, что
- 9. Суперкомпьютеры Используются неэффективно и далеко не в полной мере Необходимы: Вычислительное ядро: адаптация алгоритмов к архитектуре
- 12. НЕВЯЗКОЕ ОБТЕКАНИЕ КУЗОВА АВТОМОБИЛЯ (М = 0.12) СЕТКА: 430 949 УЗЛОВ, 2 430 306 ТЕТРАЭДРОВ
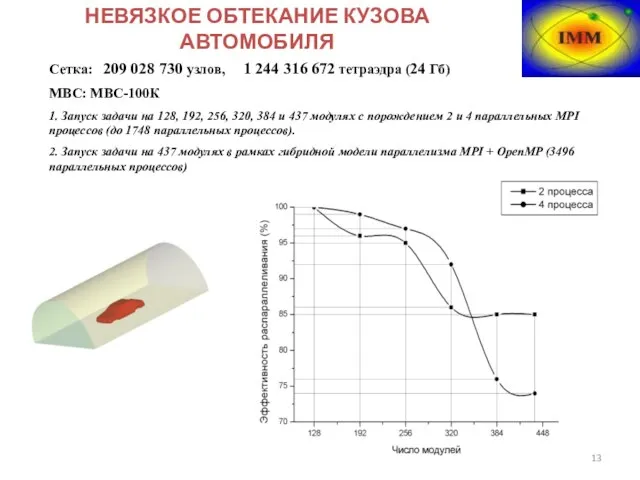
- 13. Сетка: 209 028 730 узлов, 1 244 316 672 тетраэдра (24 Гб) МВС: МВС-100К 1. Запуск
- 14. Суперкомпьютеры МСЦ РАН: процессор: Intel(R) Xeon(R) CPU X5365 @ 3.00GHz ядер на узел: 8 память узла:
- 15. Институт Математического Моделирования РАН 125047, Mиусская пл. 4а, Москва Акустика Вычислительные эксперименты по ЗПК
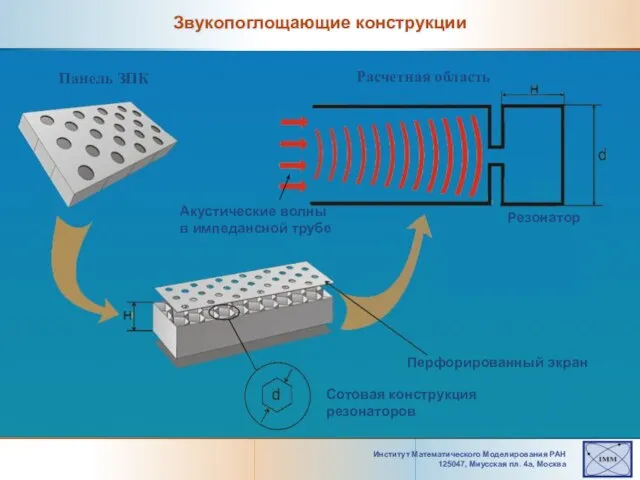
- 16. Институт Математического Моделирования РАН 125047, Mиусская пл. 4а, Москва Звукопоглощающие конструкции Панель ЗПК Расчетная область Резонатор
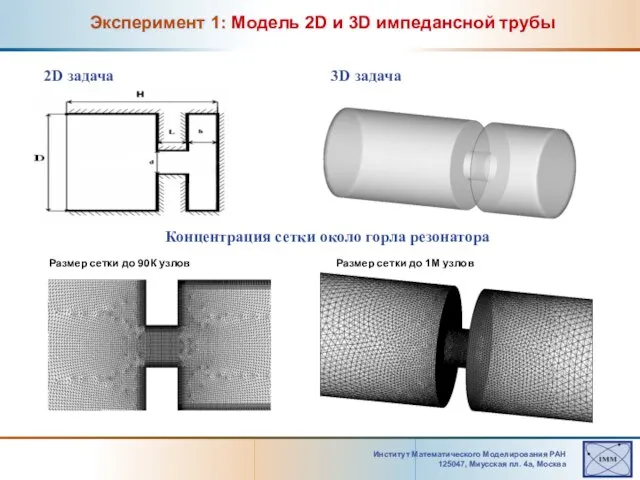
- 17. Институт Математического Моделирования РАН 125047, Mиусская пл. 4а, Москва Эксперимент 1: Модель 2D и 3D импедансной
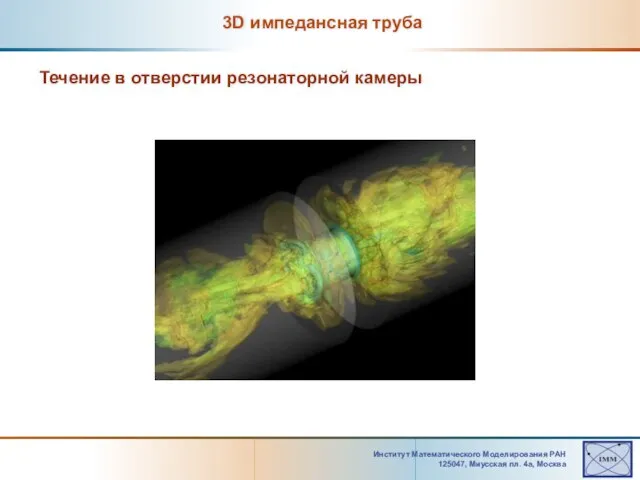
- 18. Институт Математического Моделирования РАН 125047, Mиусская пл. 4а, Москва 3D импедансная труба Течение в отверстии резонаторной
- 19. Институт Математического Моделирования РАН 125047, Mиусская пл. 4а, Москва Эффект свиста Слой смешения Возмущения плотности Эксперимент
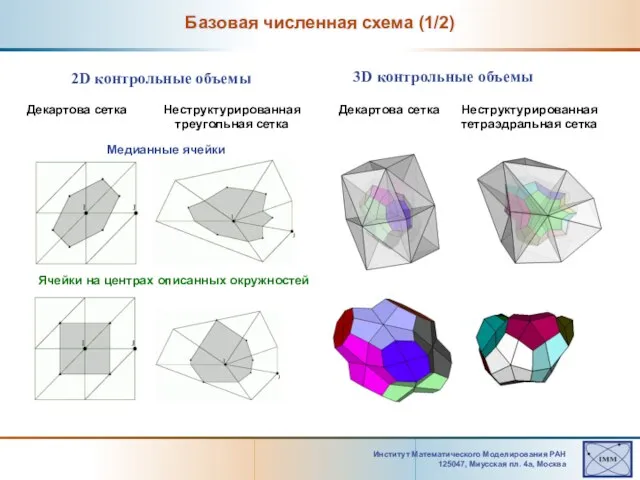
- 20. Институт Математического Моделирования РАН 125047, Mиусская пл. 4а, Москва Базовая численная схема (1/2) Декартова сетка Неструктурированная
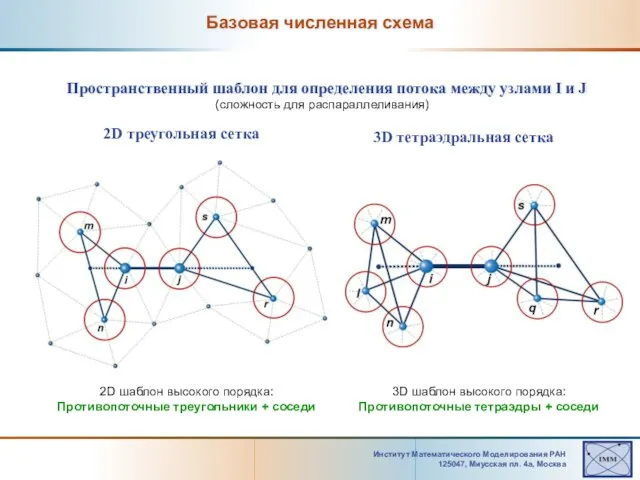
- 21. Институт Математического Моделирования РАН 125047, Mиусская пл. 4а, Москва Базовая численная схема Пространственный шаблон для определения
- 22. Институт Математического Моделирования РАН 125047, Mиусская пл. 4а, Москва Канал с 5 резонаторами Уравнения Эйлера, нет
- 23. Институт Математического Моделирования РАН 125047, Mиусская пл. 4а, Москва Heat and Mass Transfer Technological Center Colom
- 24. Статическая балансировка загрузки
- 25. Равномерное распределение суммарного веса узлов/рёбер Минимизация максимального веса исходящих из домена ребер Минимизация суммарного веса разрезанных
- 26. Чему равно 25/4 ? 6.25
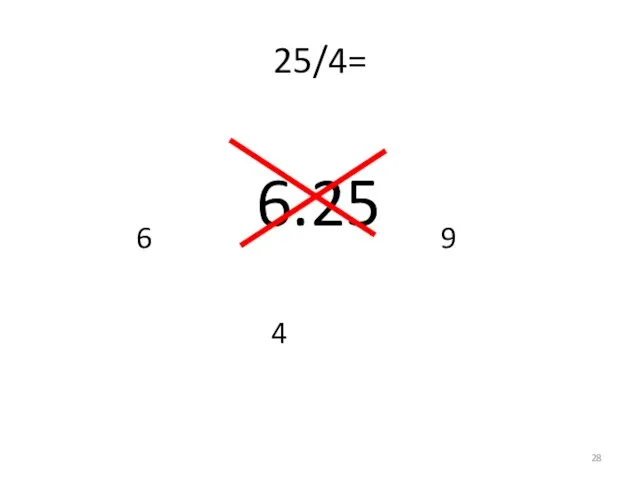
- 27. 25/4= 6.25
- 28. 25/4= 4 6 9 6.25
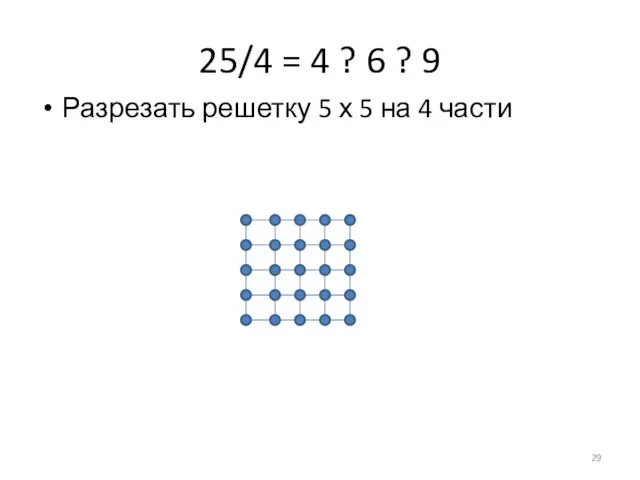
- 29. 25/4 = 4 ? 6 ? 9 Разрезать решетку 5 х 5 на 4 части
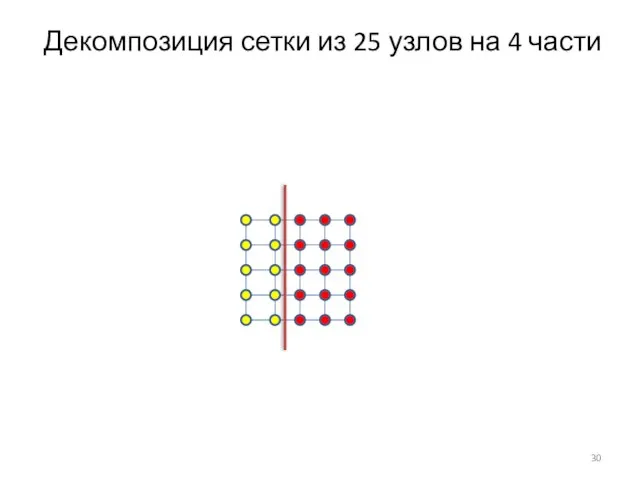
- 30. Декомпозиция сетки из 25 узлов на 4 части
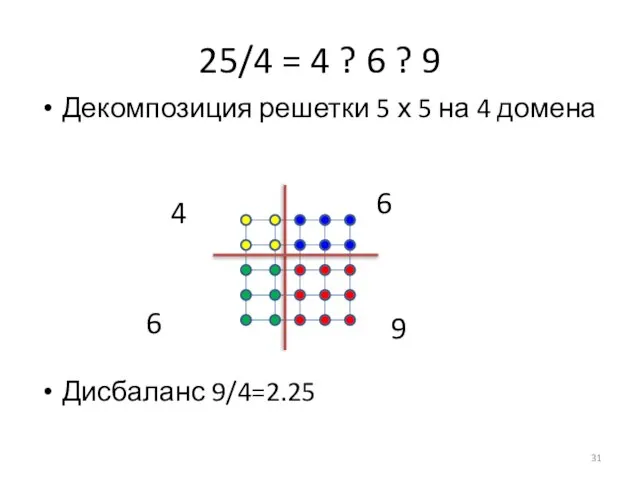
- 31. 25/4 = 4 ? 6 ? 9 Дисбаланс 9/4=2.25 Декомпозиция решетки 5 х 5 на 4
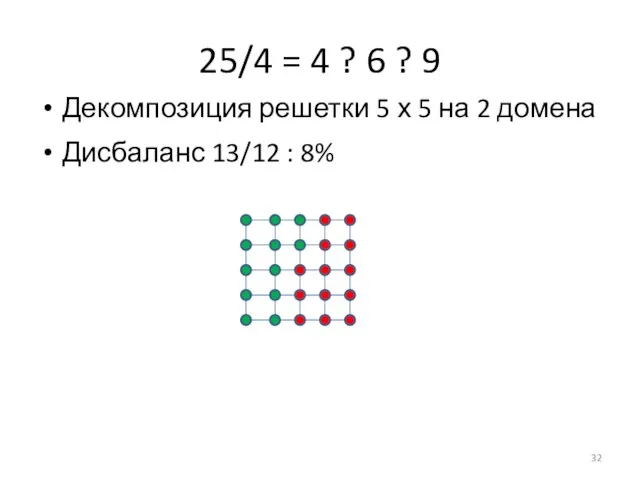
- 32. 25/4 = 4 ? 6 ? 9 Дисбаланс 13/12 : 8% Декомпозиция решетки 5 х 5
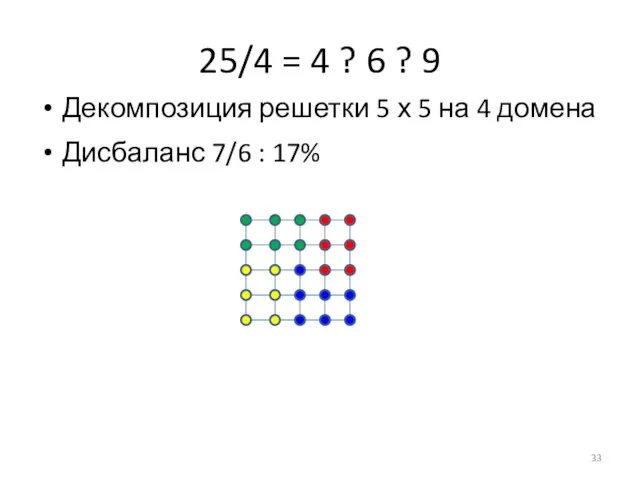
- 33. 25/4 = 4 ? 6 ? 9 Дисбаланс 7/6 : 17% Декомпозиция решетки 5 х 5
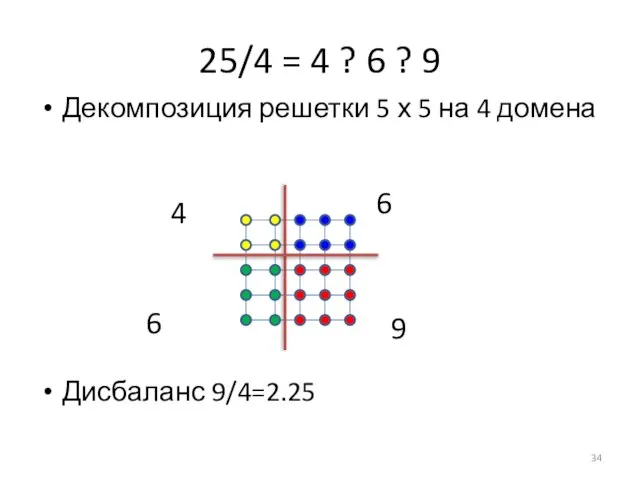
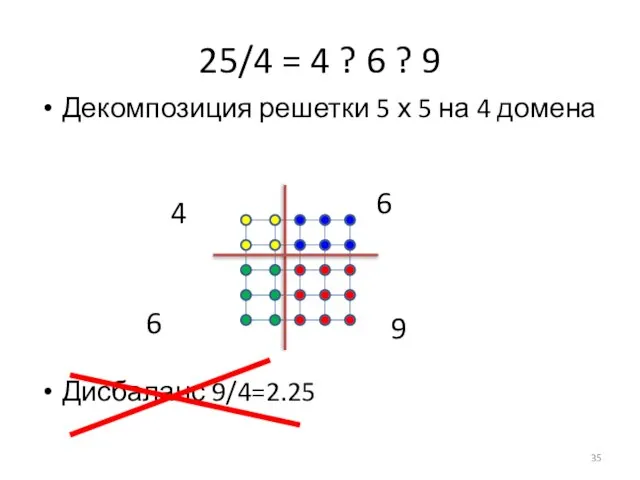
- 34. 25/4 = 4 ? 6 ? 9 Дисбаланс 9/4=2.25 Декомпозиция решетки 5 х 5 на 4
- 35. 25/4 = 4 ? 6 ? 9 Дисбаланс 9/4=2.25 Декомпозиция решетки 5 х 5 на 4
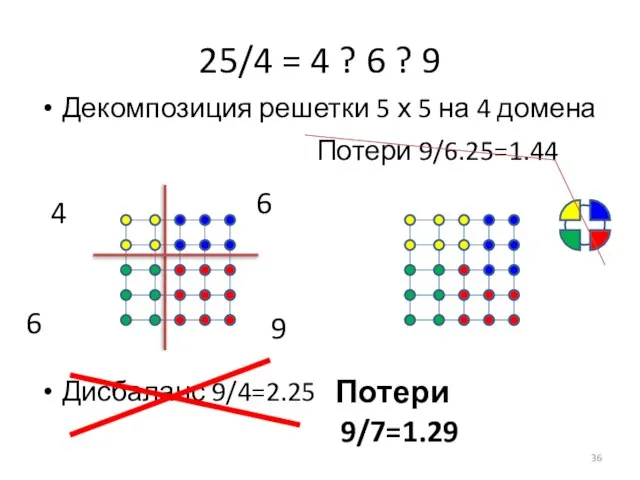
- 36. Дисбаланс 9/4=2.25 25/4 = 4 ? 6 ? 9 Декомпозиция решетки 5 х 5 на 4
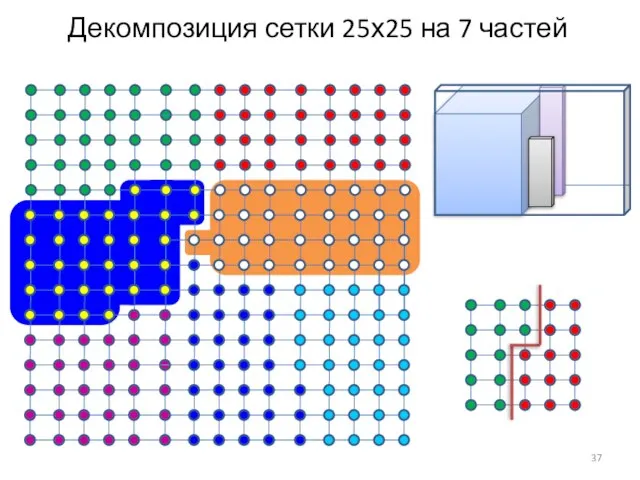
- 37. Декомпозиция сетки 25х25 на 7 частей
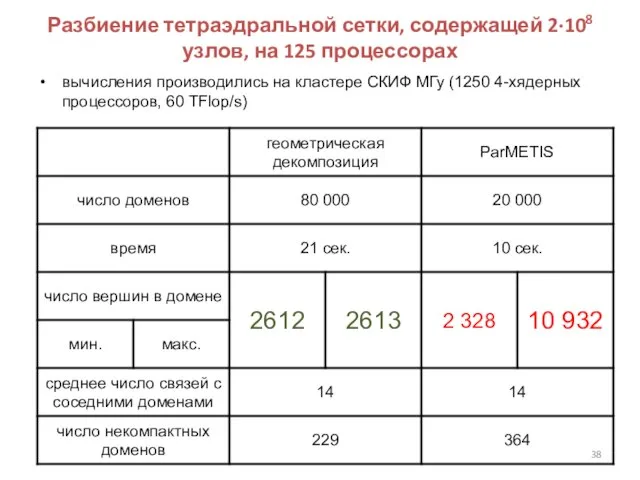
- 38. Разбиение тетраэдральной сетки, содержащей 2∙108 узлов, на 125 процессорах вычисления производились на кластере СКИФ МГу (1250
- 39. Фрагмент треугольной сетки из 75790 вершин результат геометрической декомпозиции результат перераспределения малых блоков вершин
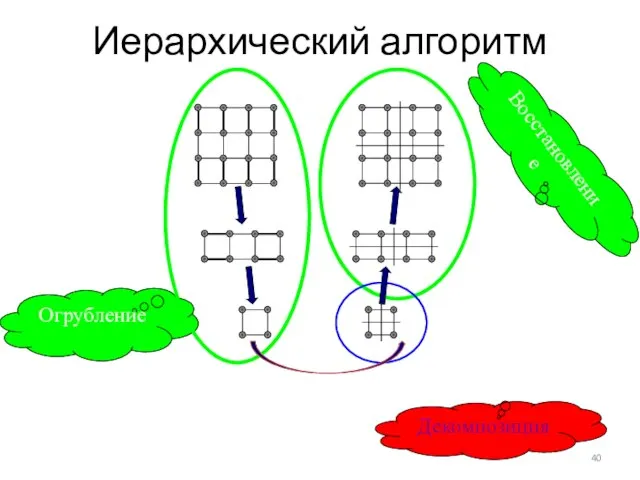
- 40. Иерархический алгоритм Огрубление Восстановление Декомпозиция
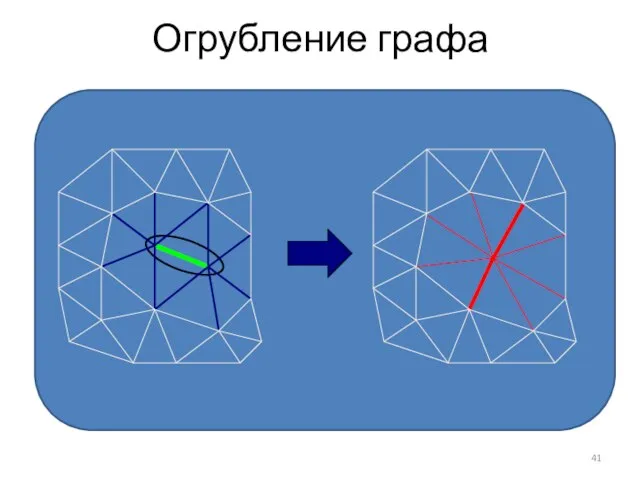
- 41. Огрубление графа
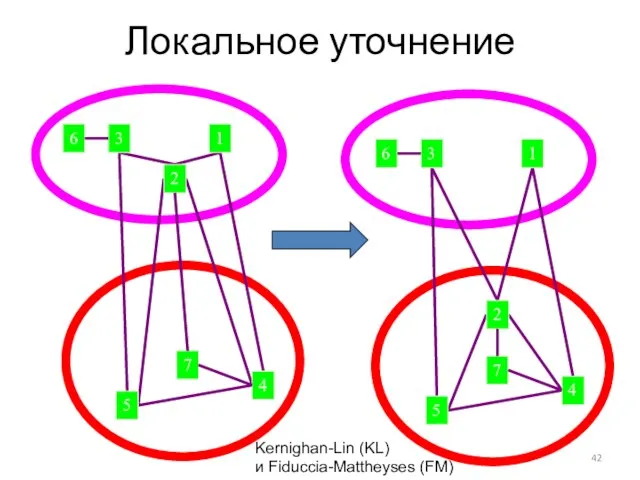
- 42. Локальное уточнение 1 3 5 4 2 6 7 1 3 5 4 2 6 7
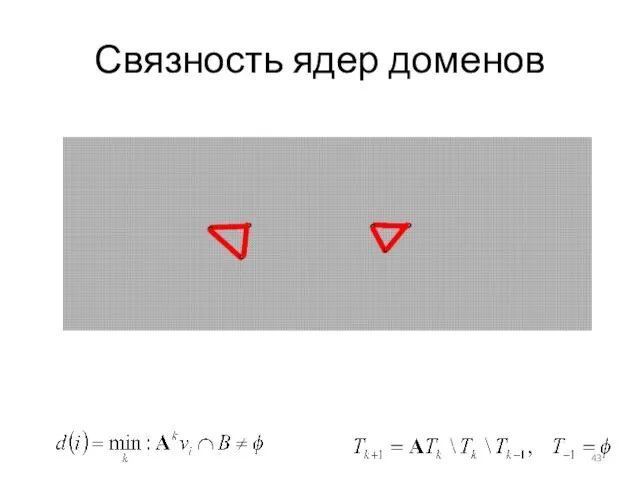
- 43. Связность ядер доменов
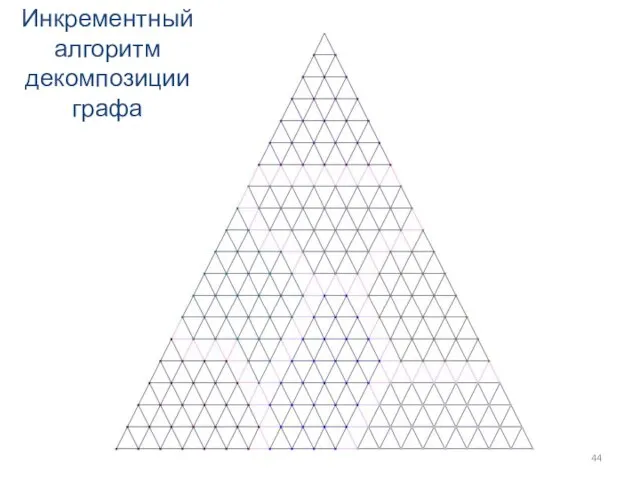
- 44. Инкрементный алгоритм декомпозиции графа
- 45. Редуцирование доменов
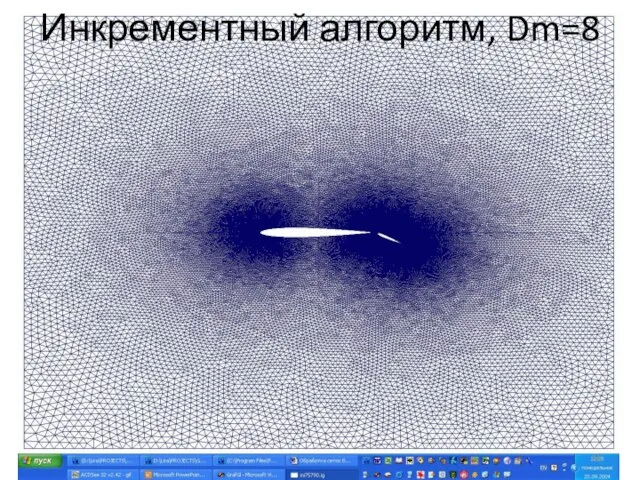
- 46. Инкрементный алгоритм, Dm=8
- 47. Инкрементный алгоритм, Dm=25
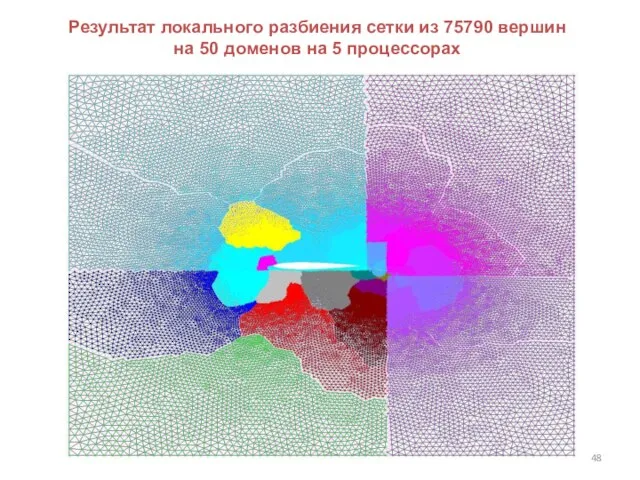
- 48. Результат локального разбиения сетки из 75790 вершин на 50 доменов на 5 процессорах
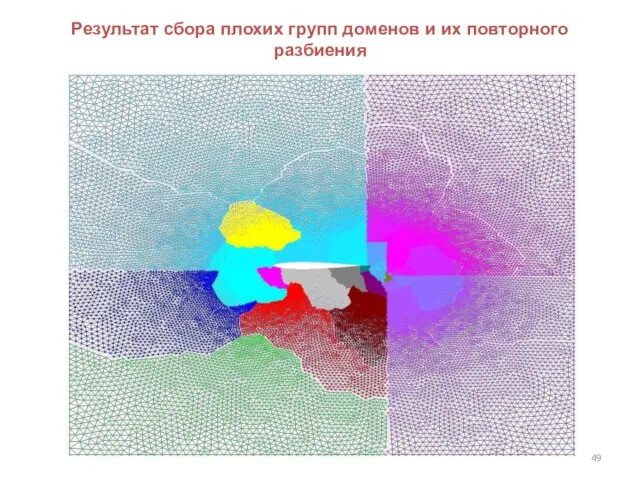
- 49. Результат сбора плохих групп доменов и их повторного разбиения
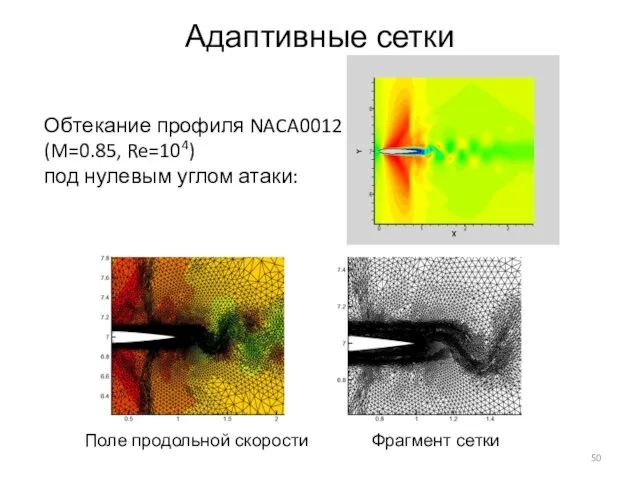
- 50. Адаптивные сетки Обтекание профиля NACA0012 (M=0.85, Re=104) под нулевым углом атаки: Поле продольной скорости Фрагмент сетки
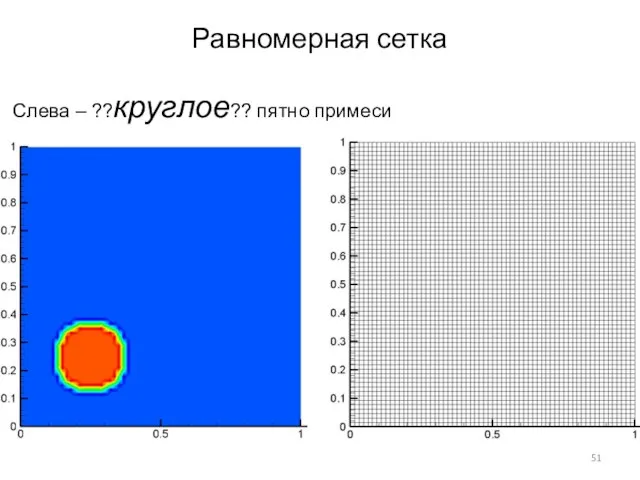
- 51. Равномерная сетка Слева – ??круглое?? пятно примеси
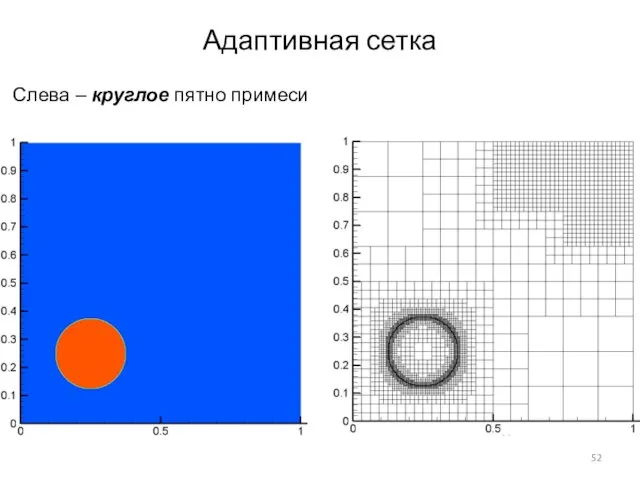
- 52. Адаптивная сетка Слева – круглое пятно примеси
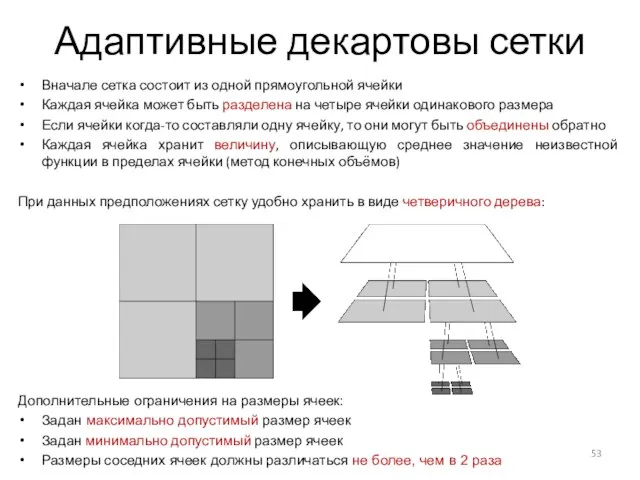
- 53. Адаптивные декартовы сетки Вначале сетка состоит из одной прямоугольной ячейки Каждая ячейка может быть разделена на
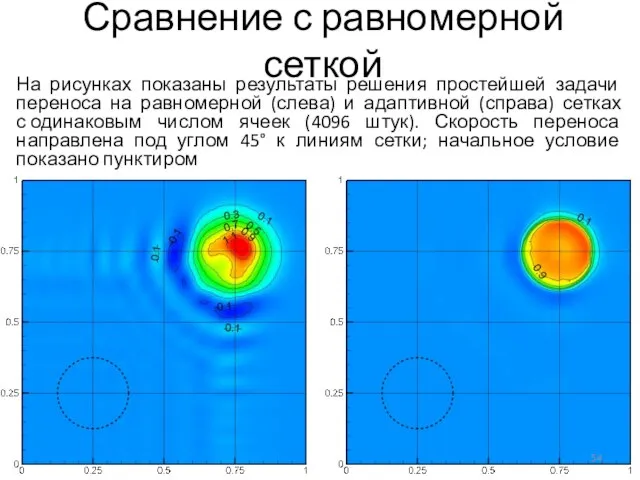
- 54. На рисунках показаны результаты решения простейшей задачи переноса на равномерной (слева) и адаптивной (справа) сетках с
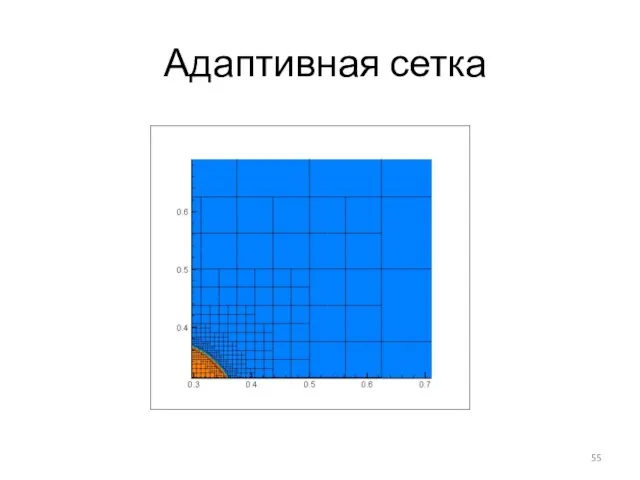
- 55. Адаптивная сетка
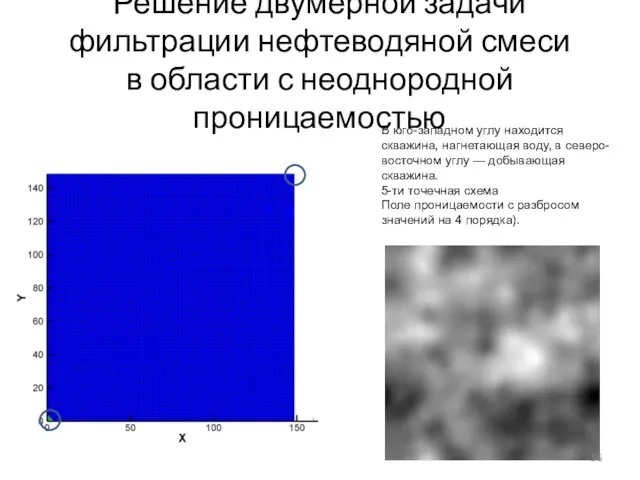
- 56. Решение двумерной задачи фильтрации нефтеводяной смеси в области с неоднородной проницаемостью В юго-западном углу находится скважина,
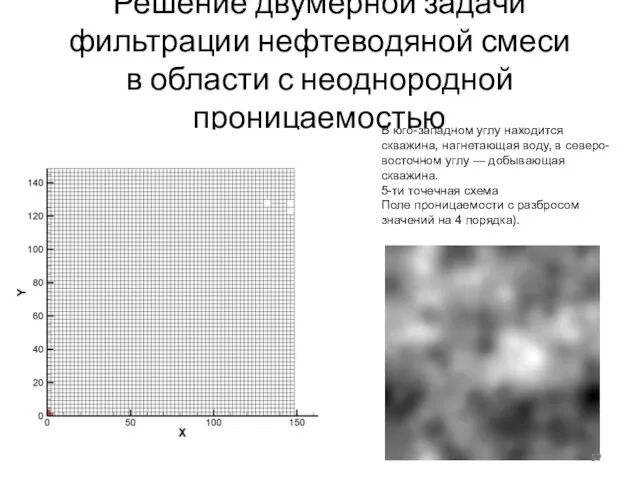
- 57. Решение двумерной задачи фильтрации нефтеводяной смеси в области с неоднородной проницаемостью В юго-западном углу находится скважина,
- 58. Динамическая балансировка загрузки Перераспределение вычислительных узлов между процессорами необходимо: При изменение конфигурации сетки При изменение вычислительной
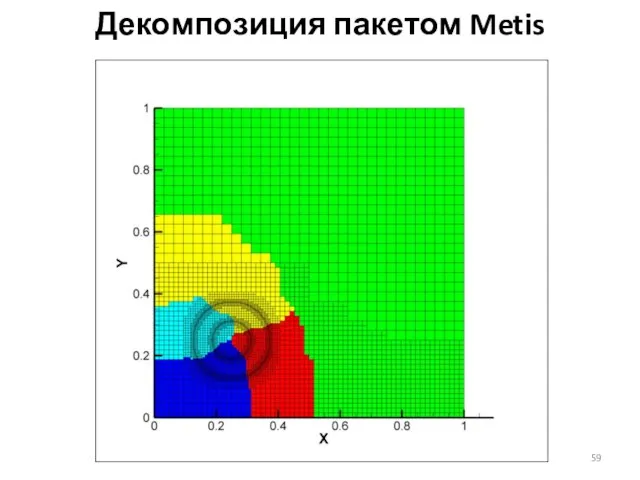
- 59. Декомпозиция пакетом Metis
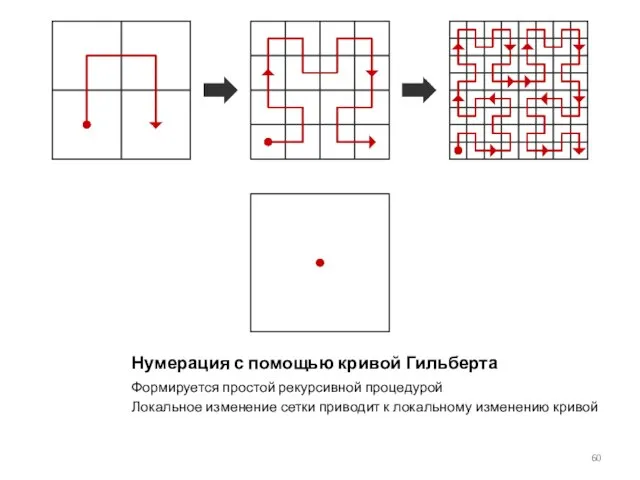
- 60. Нумерация с помощью кривой Гильберта Формируется простой рекурсивной процедурой Локальное изменение сетки приводит к локальному изменению
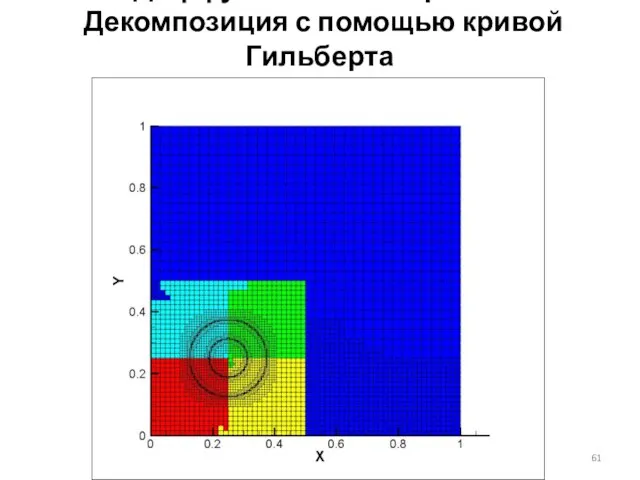
- 61. Диффузная балансировка Декомпозиция с помощью кривой Гильберта
- 63. Стратегии балансировки загрузки Wij - вычислительная нагрузка, ассоциированная с узлом сетки i на шаге j Wij
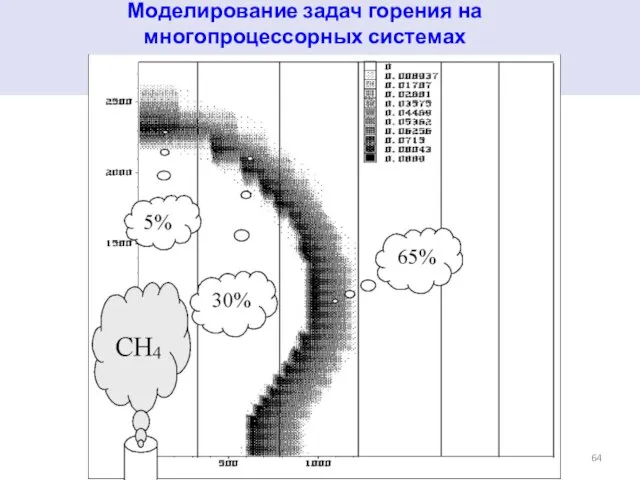
- 64. Моделирование задач горения на многопроцессорных системах
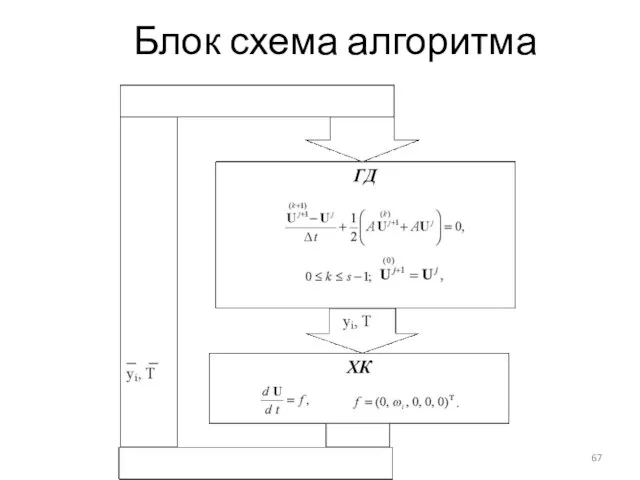
- 66. Здесь A оператор, ρ - плотность, y(i) – массовые доли i-х компонент, u, v - скорости,
- 67. Блок схема алгоритма
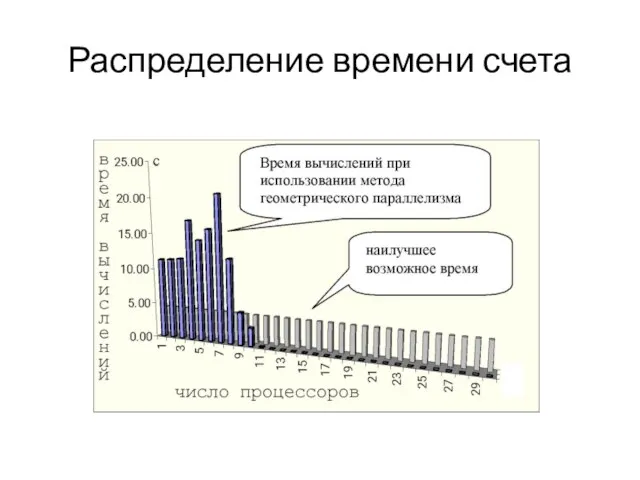
- 68. Распределение времени счета
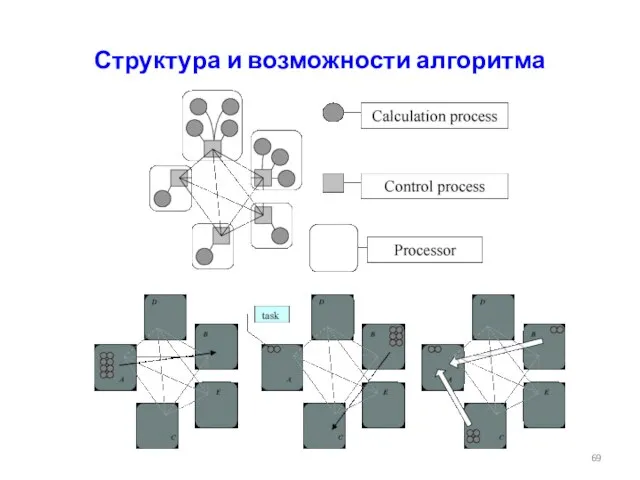
- 69. Структура и возможности алгоритма
- 70. Сотояния обрабатывающего процесса занят - если установлен соответствующий флаг. Этот флаг устанавливается перед передачей обрабатывающему процессу
- 71. Управляющий процесс 1. если - есть необработанные точки (неважно локальные или внешние) и - обрабатывающий процесс
- 72. Управляющий процесс 2. если - нет локальных необработанных точек и - нет внешних точек и -
- 73. Управляющий процесс Иначе (если не 2) 3. если - все переданные точки получены обратно обработанными и
- 74. Управляющий процесс 4. получить очередное сообщение от любого процессора или от своего обрабатывающего процесса. 5. обработать
- 75. Окончание при выполнение всех условий: нет локальных необработанных точек нет внешних точек нет обрабатываемых точек всем
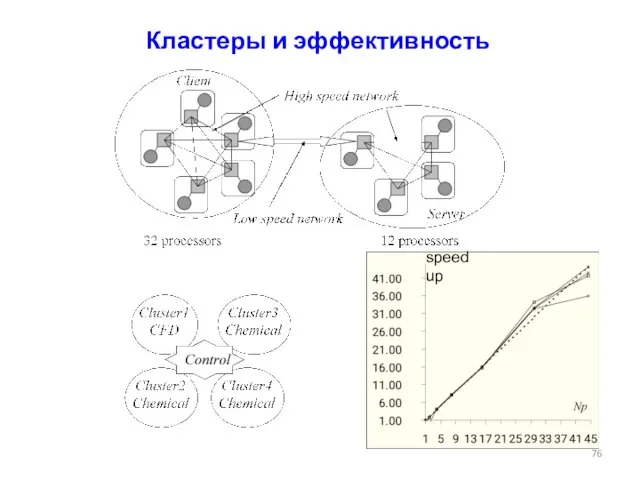
- 76. Кластеры и эффективность speedup
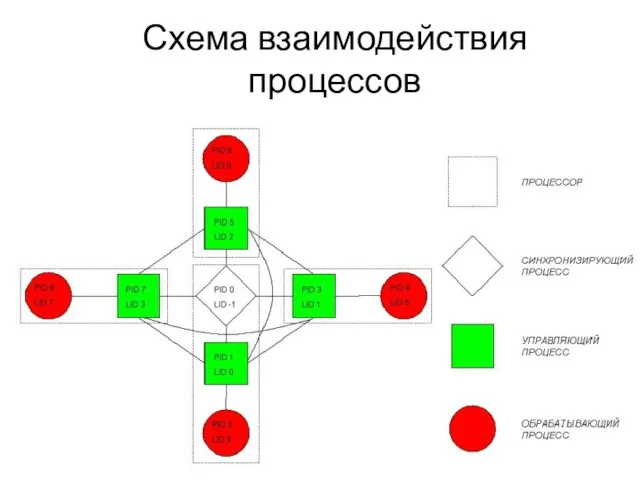
- 77. Схема взаимодействия процессов
- 79. Скачать презентацию





























 Виды сказуемых
Виды сказуемых Роль цвета в формотворчестве
Роль цвета в формотворчестве Acrobatic ROCK-N-ROLL
Acrobatic ROCK-N-ROLL СОЗДАНИЕ МУЛЬТИМЕДИЙНЫХ ПРЕЗЕНТАЦИЙ
СОЗДАНИЕ МУЛЬТИМЕДИЙНЫХ ПРЕЗЕНТАЦИЙ Попробуйте определить город Европейского Севера по его гербу, плану и фотографиям
Попробуйте определить город Европейского Севера по его гербу, плану и фотографиям Живопись в XVII в России
Живопись в XVII в России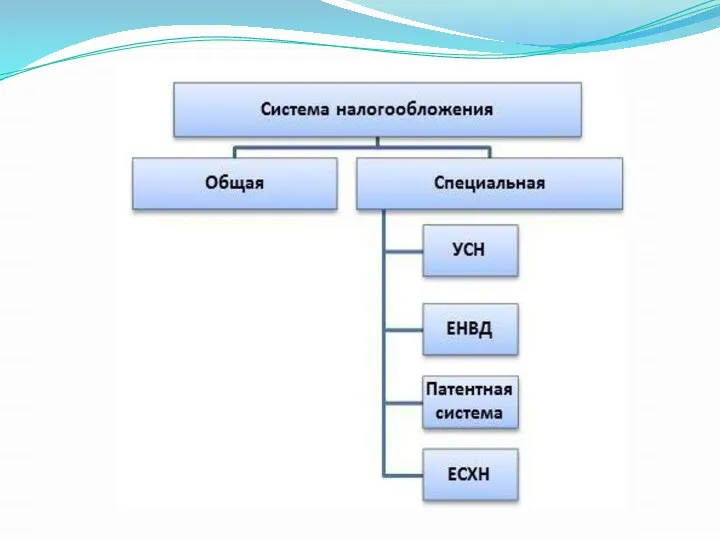 Система налогообложения
Система налогообложения Здоровые зубы как один из показателей здорового образа жизни
Здоровые зубы как один из показателей здорового образа жизни Мир верх ногами
Мир верх ногами Александр Невский
Александр Невский Сложение с числом ноль
Сложение с числом ноль Сущность менеджмента
Сущность менеджмента Родственно-контрастные сочетания
Родственно-контрастные сочетания Метательный и пневматический тир
Метательный и пневматический тир Тип Круглые червиВид Аскарида человеческая
Тип Круглые червиВид Аскарида человеческая ТМ Раптор Сроки проведения: 25 апреля – 25 мая 2012 г. Участники: оптовые клиенты нашего сайта Механика ТМ РАПТОР: за заказ акционной ма
ТМ Раптор Сроки проведения: 25 апреля – 25 мая 2012 г. Участники: оптовые клиенты нашего сайта Механика ТМ РАПТОР: за заказ акционной ма Белорусский государственный университетхимический факультетМагистерская диссертация на тему:Электрохимическое формировани
Белорусский государственный университетхимический факультетМагистерская диссертация на тему:Электрохимическое формировани Лекарство от стресса
Лекарство от стресса Учебная техника
Учебная техника Презентация на тему Тунгусский метеорит
Презентация на тему Тунгусский метеорит  Контраст тёмного и светлого пятна
Контраст тёмного и светлого пятна Loisirs. Le lexique
Loisirs. Le lexique «СОЗДАНИЕ И ВНЕДРЕНИЕ В ПРАКТИКУ ПРЕПОДАВАНИЯ СИСТЕМЫ ЦЕННОСТНО-ОРИЕНТИРОВАННЫХ ЭЛЕКТИВНЫХ КУРСОВ НА ОСНОВЕ КУЛЬТУРОЛОГИЧЕСКОГ
«СОЗДАНИЕ И ВНЕДРЕНИЕ В ПРАКТИКУ ПРЕПОДАВАНИЯ СИСТЕМЫ ЦЕННОСТНО-ОРИЕНТИРОВАННЫХ ЭЛЕКТИВНЫХ КУРСОВ НА ОСНОВЕ КУЛЬТУРОЛОГИЧЕСКОГ Метан и его свойства
Метан и его свойства НФ ДЕОЦ. Учебный филиал Отрадненский
НФ ДЕОЦ. Учебный филиал Отрадненский Светофорик приглашает
Светофорик приглашает Мясные блюда и полуфабрикаты
Мясные блюда и полуфабрикаты Страхование экологических рисков
Страхование экологических рисков