Слайд 2Спрос на деньги
Трансакционный
Мотив предосторожности
Спекулятивный

Слайд 3Шок ликвидности
Шок ликвидности ≠ «шок потери ликвидности»
Шок ликвидности – неожиданная потребность в

наличных средствах
Неожиданная – заранее не можем сказать, понадобятся ли средства
Наличных – средствах, которые без промедления можно «пустить в дело»
Слайд 4Страхование шоков ликвидности: домохозяйство
На основе:
Diamond D.W., Dybvig Ph.H. (1983) “Bank Runs, Deposit

Insurance, and Liquidity”, JPE, 91(3), 401-419
Шок ликвидности домохозяйства
почему?
Слайд 5Модель Даймонда-Дибвига
3 периода: t=0,1,2
1 благо (для потребления и инвестиций)
Континуум домохозяйств.
t=0: у каждого

домохозяйства есть единица блага, которую можно хранить без потерь или инвестировать
Производственная технология (R>1):
t=0 t=1 t=2
-1 0 R
1 0
Постоянная отдача от масштаба
Слайд 6Модель Даймонда-Дибвига (2)
Домохозяйство типа 1: U(c1)= u(c1) (шок ликвидности)
Домохозяйство типа 2: U(c1,

c2)= ρu(c1+c2),
ρ – дисконт
t=1: домохозяйства узнают свой тип (α - вероятность быть домохозяйством 1 типа)
U(c) – “хорошая” функция:
Коэффициент относительного неприятия риска:
Слайд 7Модель Даймонда-Дибвига (3)
Выбор домохозяйства (сij – потребление домохозяйства типа i в период

j):
Является ли выбор оптимальным?
Оптимальный выбор: домохозяйство максимизирует ожидаемую функцию полезности:
Слайд 8Модель Даймонда-Дибвига (4)
Банк
не различает типы потенциальных вкладчиков
предлагает вклад до востребования

Слайд 11Как это работает (3)
Вкладчиков много – можно диверсифицировать риски
Механизм инвестирования:

Слайд 12Набеги вкладчиков и банковские паники
Теория самосбывающихся ожиданий
Теория единственного равновесия
Теория информационных сигналов
Банковская

паника, Чикаго
Слайд 13Определения
Набеги вкладчиков
Эффективные
Неэффективные
Макрофакторы
Прочие информационные сигналы
Проблема координации
Банковские паники
БП I типа: асимметрия информации и

«эффект заражения»
БП II типа: макроэкономические факторы
Слайд 14Банковские паники II типа
Гипотезы по Гортону (Gorton, 1988):
Сезонная гипотеза
Крупное банкротство
Рецессионная гипотеза
После пика
Рациональное

поведение вкладчиков
Ожидания
Приближение рецессии
Кредиты: меньше и дороже
Слайд 15Теория самосбывающихся ожиданий
На основе
Diamond D.W., Dybvig Ph.H. (1983) “Bank Runs, Deposit Insurance,

and Liquidity”, JPE, 91(3), 401-419
Набег вкладчиков реализуется как одно из возможных равновесий на рынке банковских вкладов, в качестве самосбывающегося ожидания
Слайд 16Модель Даймонда-Дибвига
Однако средства банка в первом периоде не безграничны.
где fj –

количество вкладчиков до вкладчика j в очереди, f – общее количество изъятий в первом периоде
Если вкладчик второго типа ожидает, что другие вкладчики второго типа изымут свои средства, он предпочтет сделать то же самое.
Слайд 17Модель Даймонда-Дибвига (2)
2 вкладчика
Ставка 1 периода – 1,4
Ставка 2 периода – 1,6

Слайд 18Теория единственного равновесия
На основе
Postlewaite A., Vives X., (1997) “Bank Runs as an

Equilibrium Phenomenon”, JPE, 95(3), 485-491
При определенных условиях набег вкладчиков может реализовываться как единственное равновесие в модели.
Слайд 19Модель Постлвейта-Вивеса
Периоды: t=0,1,2,3
Производственная технология:
2 агента, 3 типа:
U(с)= u(c1)
U(c)= u(c1 + c2)
U(c)=

u(c1 + c2 + c3)
Стратегии изъятия: α1, α2, α3.
Контракт: изъятие в первом и втором периоде – без потерь (1)
Слайд 20Модель Постлвейта-Вивеса (2)
Выигрыши

Слайд 21Модель Постлвейта-Вивеса (3)
В равновесии вкладчики 1 и 2 типа изымают в первый

период, вкладчики 3 типа ждут третьего периода
Если
Слайд 22Модель Постлвейта-Вивеса (4)
Нет в модели:
вкладчики 3го типа?
1 из равновесий – набег, если:
Или:

Слайд 23Теория информационных сигналов
На основе
Jacklin Ch. J., Bhattacharya S. (1988) “Distinguishing Panics and

Information-based Bank Runs: Welfare and Policy Implications”, JPE, 96(3), 568-592
Набег вкладчиков возникает в ответ на негативные информационные сигналы.
Слайд 24Модель Джеклин-Бхаттачарья
Периоды: T=0,1,2
Производственная технология: период 2
RL с вероятностью θ
RH с вероятностью 1-θ,

RH >1, RH > RL
Континуум агентов
U(c1, c2, K)= u(c1)+ ρK u(c2), K=1 с вероятностью t, ρ2 > ρ1
Пусть:
u(c) = c1/2
ρ1 = ρ<1, ρ2 = 1
Информация:
В момент времени T=1, доля α вкладчиков типа 2 получает уточненную информацию θ*
Слайд 27Модель Джеклин-Бхаттачарья (4)
При росте θ условие совместимости по стимулам для вкладчиков типа

2 может не выполняться.
«Пограничный уровень» θ
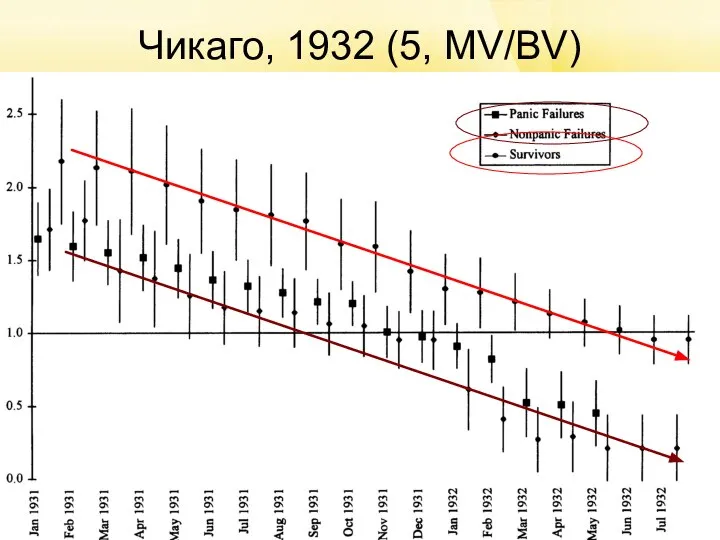
Слайд 28Чикаго, 1932
Пример:
Calomiris C.W., Mason J.R. (1997) Contagion and Bank Failures During the

Great Depression: the June 1932 Chicago Bank Panic, American Economic Review, 87(5), 863-883
Из каких набегов вкладчиков складывается банковская паника?
Слайд 29Чикаго, 1932 (2)
Банковская паника в Чикаго, июнь 1932:
49 банкротств в штате,

40 – в Чикаго
26 – 20-27 июня
Акции стремительно падали
Были затронуты и банки без финансовых проблем
Некоторые банки закрылись, некоторые выстояли
Слайд 30Чикаго, 1932 (3)
Почему?
Падение цен на акции
Публикации о мошенничествах руководства банков (Дж. Бэйн:

девелопер+банкир)
9 июня – закрылись его банки
Финансовые проблемы муниципалитета
Активы банков – более рисковые
Муниципалитет призвал выкупить неликвидные бумаги
Работники аппарата забрали свои средства в силу задержек зарплаты
Шоки ликвидности
Слайд 31Чикаго, 1932 (4)
Группы банков
Банки, закрывшиеся в период паники (1)
Банки, не закрывшиеся в

это время (2)
Показатели
MV/BV
Прогноз вероятности банкротства (1931)
Снижение объемов вкладов
Средняя процентная ставка по привлеченным кредитам
Слайд 33Чикаго, 1932 (6)
Прогноз вероятности банкротства
(1)>(2)
Снижение объемов вкладов в 1931:
(1) 41%
(2) 33%
Ставка по

привлеченным кредитам:
(1) 0,9%
(2) 0,6%
Слайд 34Чикаго, 1932 (7)
Почему устояли банки?
Запас финансовой прочности
Эффективность набегов вкладчиков
Поддержка банков
E.g.: Central Republic
Репутация
Качество

Слайд 35Сигналы: пример
Кризис доверия, 2004
«Северная Казна», 2008
Northern Rock, 2007


































 Нормальный голос
Нормальный голос Профильное обучение: анализ ситуации и перспективы развития
Профильное обучение: анализ ситуации и перспективы развития Николай Фёдорович Ватутин
Николай Фёдорович Ватутин Spotlight 3
Spotlight 3 Полномочия субъектов государственной власти РФ
Полномочия субъектов государственной власти РФ 8р №24 Тире между подлежащим и сказуемым
8р №24 Тире между подлежащим и сказуемым Аналитический отчёт за 2019-2020 год
Аналитический отчёт за 2019-2020 год Основы эксплуатации сетей почтовой связи
Основы эксплуатации сетей почтовой связи Реформы Н.С. Хрущева:черное или белое?
Реформы Н.С. Хрущева:черное или белое? ВЕРА ТРЕБУЕТ РАЗМЫШЛЕНИЙ « 5:1 Мы знаем, что когда наша земная палатка - наше тело - будет разрушена, в небе нас ждет вечный дом, создан
ВЕРА ТРЕБУЕТ РАЗМЫШЛЕНИЙ « 5:1 Мы знаем, что когда наша земная палатка - наше тело - будет разрушена, в небе нас ждет вечный дом, создан Теплофизические свойства строительных материалов
Теплофизические свойства строительных материалов SeMail System
SeMail System Наркомания и подростки
Наркомания и подростки Понятие психики. Структура личности в психологии
Понятие психики. Структура личности в психологии Финансирование кинематографа в РФ
Финансирование кинематографа в РФ Япония Токио
Япония Токио Проект магазина Overkill
Проект магазина Overkill Макс Карл Эрнст Людвиг Планк
Макс Карл Эрнст Людвиг Планк Летняя оздоровительная смена Круиз по морям, океанам и островам
Летняя оздоровительная смена Круиз по морям, океанам и островам Квест Дипломатические проекты гимназии
Квест Дипломатические проекты гимназии american vs british words
american vs british words  Особенности организации и проведения школьного этапа Всероссийской олимпиады школьников по немецкому языку в 2011-2012 учебном году
Особенности организации и проведения школьного этапа Всероссийской олимпиады школьников по немецкому языку в 2011-2012 учебном году Молекулярная электроникаНина Викторовна Агринская (ФТИ им.Иоффе РАН, СПбГПУ)
Молекулярная электроникаНина Викторовна Агринская (ФТИ им.Иоффе РАН, СПбГПУ) Набор медведи. Резьба объемных утилитарных форм
Набор медведи. Резьба объемных утилитарных форм ГРЕЦИЯ В ПЕРВОЙ ПОЛОВИНЕ IV ВЕКА
ГРЕЦИЯ В ПЕРВОЙ ПОЛОВИНЕ IV ВЕКА РАЗРАБОТКА МЕТОДОВ ПРОГНОЗА ПРОФЕССИОНАЛЬНОЙ СРАБАТЫВАЕМОСТИ ОПЕРАТИВНОГО ПЕРСОНАЛА БЛОЧНОГО ЩИТА УПРАВЛЕНИЯ АЭС
РАЗРАБОТКА МЕТОДОВ ПРОГНОЗА ПРОФЕССИОНАЛЬНОЙ СРАБАТЫВАЕМОСТИ ОПЕРАТИВНОГО ПЕРСОНАЛА БЛОЧНОГО ЩИТА УПРАВЛЕНИЯ АЭС Эстафета олимпийского огня
Эстафета олимпийского огня Презентация на тему Десятичные дроби и действия над ними
Презентация на тему Десятичные дроби и действия над ними