Содержание
- 2. A Lower Bound for Sorting Rules for sorting. The lower bound on comparison sorting. Beating the
- 3. “if this element’s sort key is less than this other element’s sort key, then do something,
- 4. 1) each sort key is either 1 or 2, 2) the elements consist of only sort
- 5. =>go through every element and count how many of them are 1s; let’s say that k
- 6. Rules for sorting
- 7. The lower bound on comparison sorting A comparison sort is any sorting algorithm that determines the
- 8. The lower bound on comparison sorting This is the lower bound: In the worst case, any
- 9. The lower bound on comparison sorting We write: Ω-notation (It gives a lower bound) We say:
- 10. The lower bound on comparison sorting 1) Lower bound is saying something only about the worst
- 11. The lower bound on comparison sorting A universal lower bound => applies to all inputs. For
- 12. The lower bound on comparison sorting 2) The lower bound does not depend on the particular
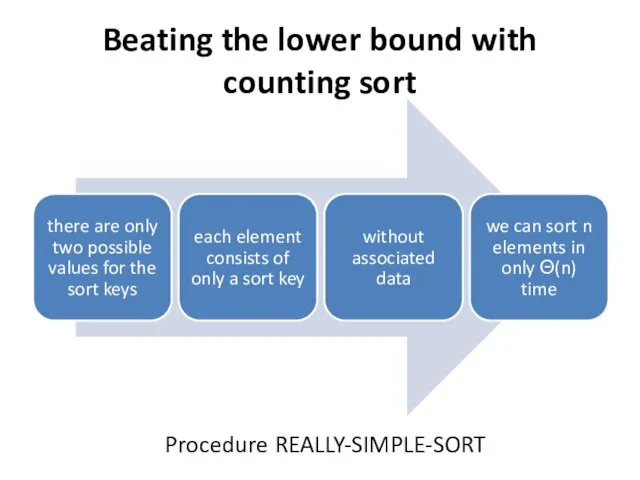
- 13. Beating the lower bound with counting sort Procedure REALLY-SIMPLE-SORT
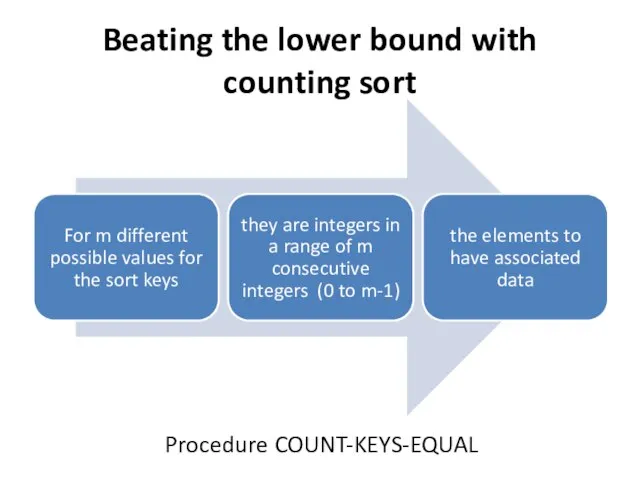
- 14. Beating the lower bound with counting sort Procedure COUNT-KEYS-EQUAL
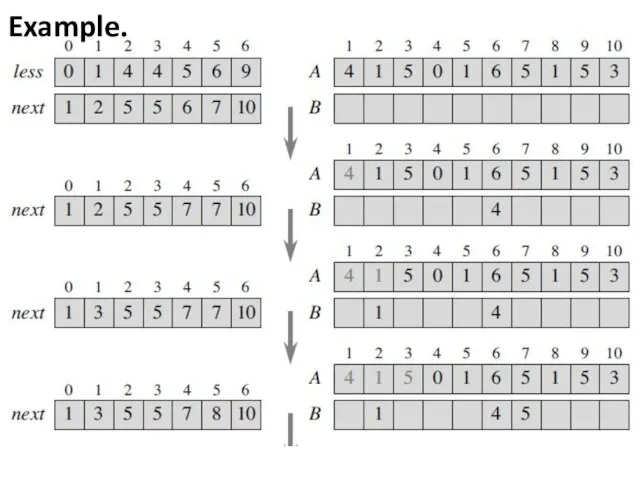
- 15. Beating the lower bound with counting sort Example. Let’s we know that the sort keys are
- 16. Beating the lower bound with counting sort Generalize. If k elements have sort keys equal to
- 17. Beating the lower bound with counting sort What should be done? We want to compute, for
- 18. Beating the lower bound with counting sort Computing: how many elements have sort keys equal to
- 19. Beating the lower bound with counting sort Notice that COUNT-KEYS-EQUAL never compares sort keys with each
- 20. Beating the lower bound with counting sort Since the first loop (step 2) makes m iterations,
- 21. Beating the lower bound with counting sort Computing: how many elements have sort keys less than
- 22. Beating the lower bound with counting sort Example. Suppose that m = 7, so that all
- 23. Beating the lower bound with counting sort Then equal = (1; 3; 0; 1; 1; 3;
- 24. Beating the lower bound with counting sort less = (0; 1; 4; 4; 5; 6; 9)equal
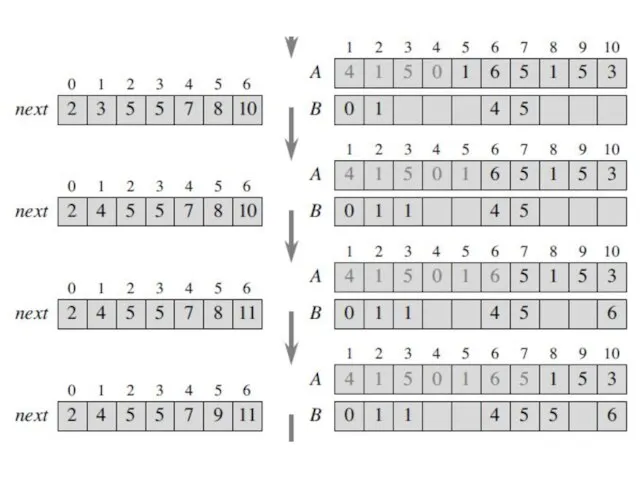
- 26. Example.
- 30. Beating the lower bound with counting sort The idea is that, as we go through the
- 31. Beating the lower bound with counting sort The loop of step 2 sets up the array
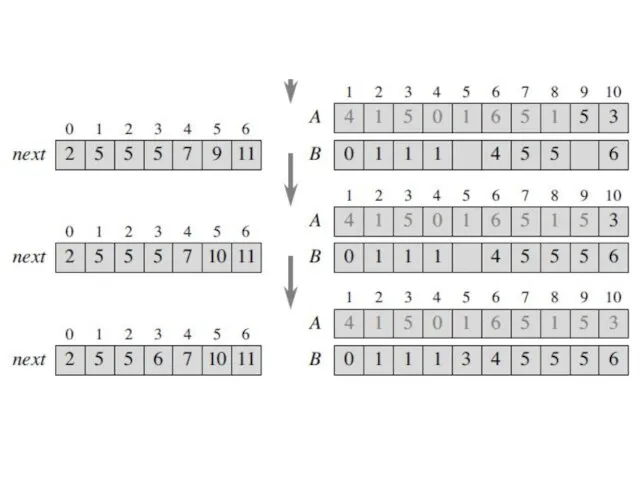
- 32. Beating the lower bound with counting sort For each element A[i], step 3A stores A[i] into
- 33. Beating the lower bound with counting sort How long does REARRANGE take? The loop of step
- 34. Beating the lower bound with counting sort Counting sort
- 35. Beating the lower bound with counting sort The running times of COUNT-KEYS-EQUAL Θ(m+n); COUNTKEYS-LESS Θ(m); REARRANGE
- 36. Beating the lower bound with counting sort Counting sort beats the lower bound of Ω(n lg
- 37. Beating the lower bound with counting sort If the sort keys were real numbers with fractional
- 38. Beating the lower bound with counting sort The running time is Θ(n) if m is a
- 39. Beating the lower bound with counting sort Sorting exams by grade. The grades range from 0
- 40. Beating the lower bound with counting sort Counting sort has another important property: it is stable.
- 41. Radix sort Let’s you had to sort strings of characters of some fixed length. For example,
- 42. Radix sort 36 characters => numeric from 0 to 35 The code for a digit =>
- 43. Radix sort Simple example. Confirmation code comprises two characters. using the rightmost character as the sort
- 44. Radix sort Simple example. BUT using the leftmost character as the sort key using the rightmost
- 45. Radix sort Example.
- 47. Скачать презентацию

























![Beating the lower bound with counting sort For each element A[i], step](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/851702/slide-31.jpg)













 Линейная перспектива. Тема №5
Линейная перспектива. Тема №5 Искусственный интеллект
Искусственный интеллект Трудовое право
Трудовое право Debtprice - долговой портал, Digital - решение по купле-продаже кредитных дел
Debtprice - долговой портал, Digital - решение по купле-продаже кредитных дел Методика маржинального анализа прибыли
Методика маржинального анализа прибыли Птичкин дом.
Птичкин дом. На завод металлоконструкций требуются специалисты
На завод металлоконструкций требуются специалисты Формы обучения персонала
Формы обучения персонала Классный час «Шаг в пропасть… Опасно это или нет?» (вредные привычки) Автор: социальный педагог Болычевская Дарья Юрьевна МКОУ «Новосидоровская СОШ» Курганской области
Классный час «Шаг в пропасть… Опасно это или нет?» (вредные привычки) Автор: социальный педагог Болычевская Дарья Юрьевна МКОУ «Новосидоровская СОШ» Курганской области БИРЖЕВЫЕ НОВОСТИ –КАКИМИ ИМ БЫТЬ?На примере распространения информации Казахстанской фондовой биржей (KASE)
БИРЖЕВЫЕ НОВОСТИ –КАКИМИ ИМ БЫТЬ?На примере распространения информации Казахстанской фондовой биржей (KASE) ПЕРВАЯ ИНЖЕНЕРНАЯКОМПАНИЯ
ПЕРВАЯ ИНЖЕНЕРНАЯКОМПАНИЯ осторожно животные
осторожно животные Общее устройство автомобилей и тракторов
Общее устройство автомобилей и тракторов  Принципы управления персоналом
Принципы управления персоналом Выполнение задания части 3 (С) ЕГЭ
Выполнение задания части 3 (С) ЕГЭ Презентация на тему Духовная жизнь
Презентация на тему Духовная жизнь Что такое салфетка?
Что такое салфетка? Защита информации
Защита информации Общество с ограниченной ответственностью (ООО)
Общество с ограниченной ответственностью (ООО) Адаптация детей к детскому саду
Адаптация детей к детскому саду Сбор и ввод нормативной информации при внедрении ERP
Сбор и ввод нормативной информации при внедрении ERP История мирного атома в России: ледокол «Ленин»
История мирного атома в России: ледокол «Ленин» Урок 11 Експериментальна робота №3
Урок 11 Експериментальна робота №3 Новые явления в экономике. Россия в XVII веке
Новые явления в экономике. Россия в XVII веке Проект «Библиодилижанс»
Проект «Библиодилижанс» Типовые IP-решения
Типовые IP-решения Інформатика в початковій школі
Інформатика в початковій школі ПУТЕШЕСТВИЕ ПО ВОЕННО-ГРУЗИНСКОЙ ДОРОГЕ
ПУТЕШЕСТВИЕ ПО ВОЕННО-ГРУЗИНСКОЙ ДОРОГЕ