Центральная симметрия

Центральная симметрия.
Определение:
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.

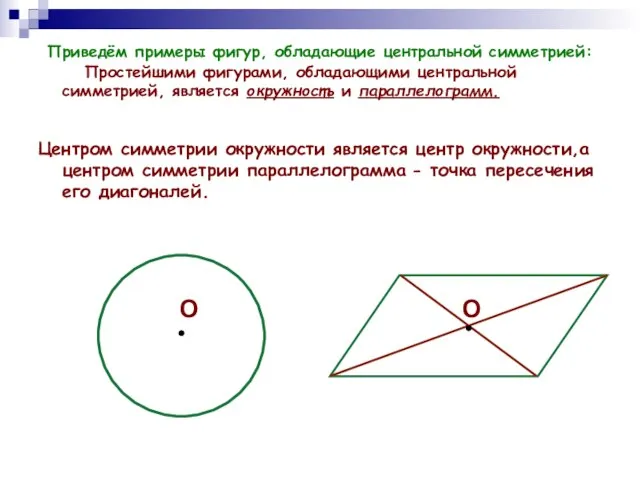
Приведём примеры фигур, обладающие центральной симметрией:
Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм.
Центром симметрии окружности является центр окружности,а центром симметрии параллелограмма - точка пересечения его диагоналей.
O
O

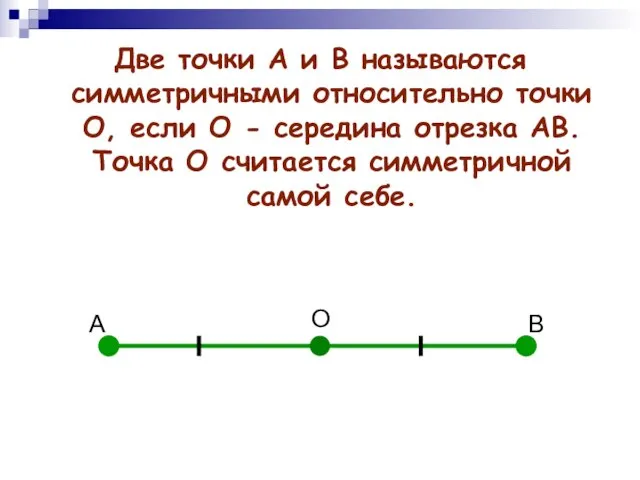
А
В
О
Две точки А и В называются симметричными относительно точки О, если О - середина отрезка АВ. Точка О считается симметричной самой себе.

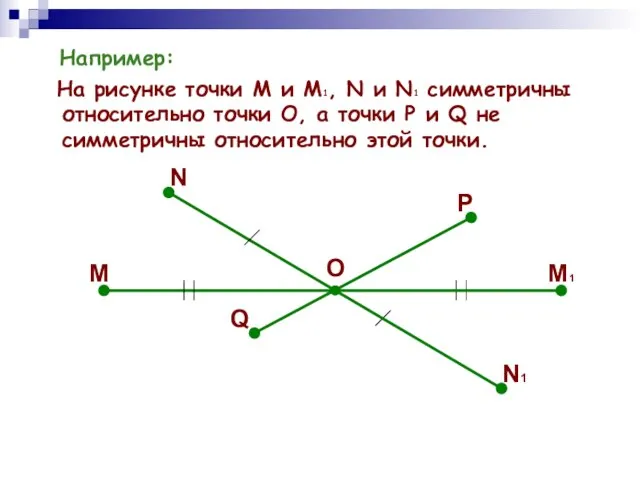
Например:
На рисунке точки М и М1, N и N1 симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.
М
М1
N
N1
О
Р
Q

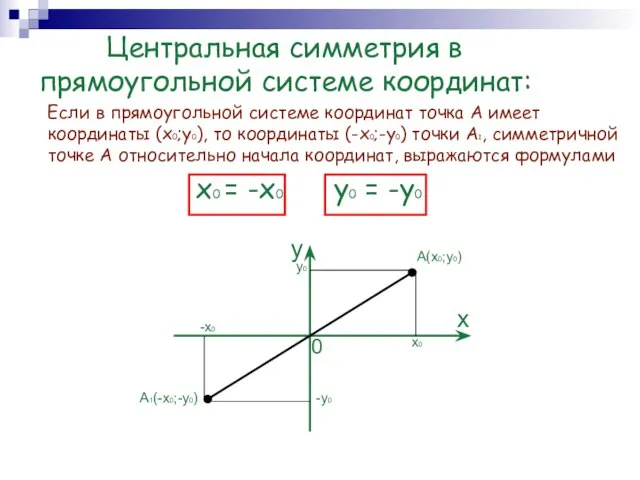
Центральная симметрия в прямоугольной системе координат:
Если в прямоугольной системе координат точка А имеет координаты (x0;y0), то координаты (-x0;-y0) точки А1, симметричной точке А относительно начала координат, выражаются формулами
x0 = -x0 y0 = -y0
у
х
0
А(x0;y0)
А1(-x0;-y0)
x0
-x0
y0
-y0

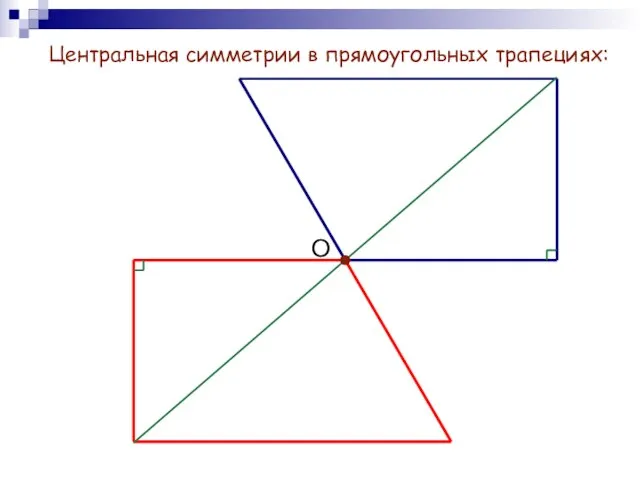
Центральная симметрии в прямоугольных трапециях:
О

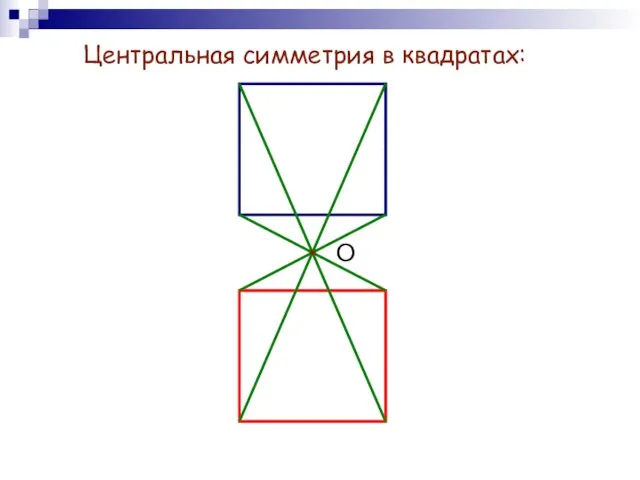
Центральная симметрия в квадратах:
О

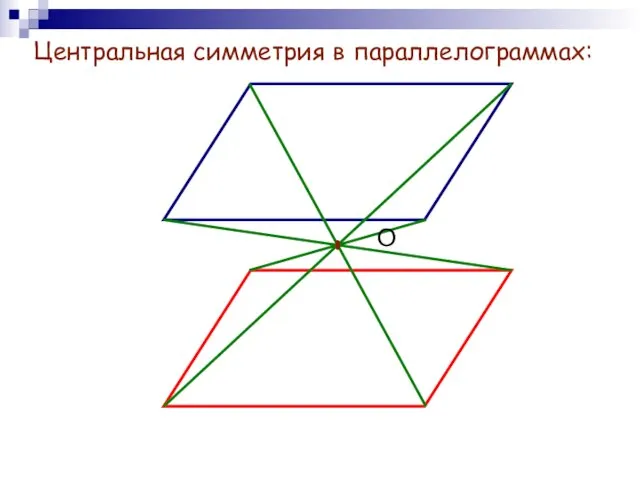
Центральная симметрия в параллелограммах:
О

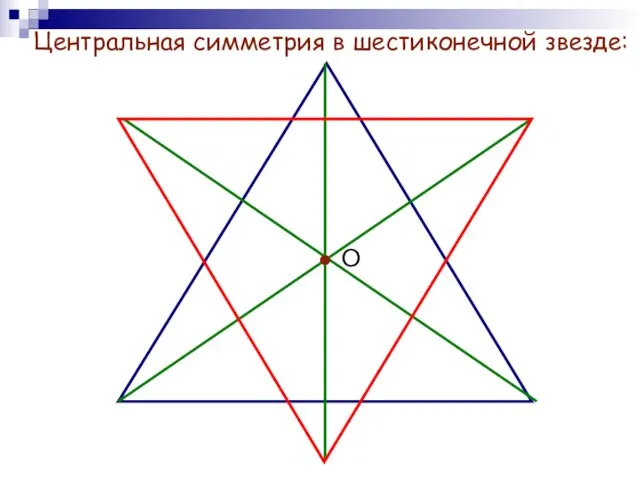
Центральная симметрия в шестиконечной звезде:
О

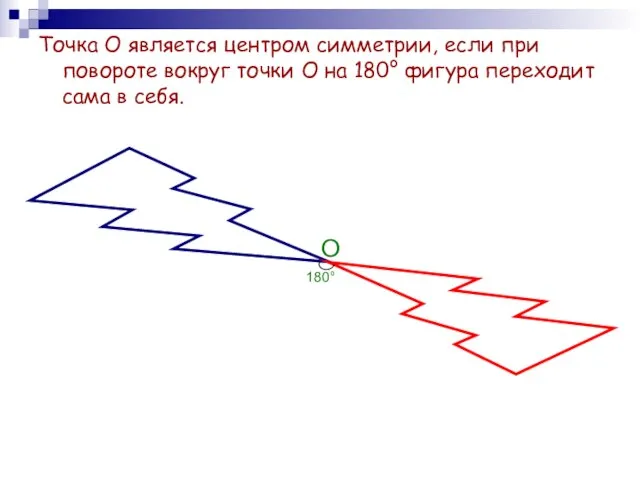
Точка О является центром симметрии, если при повороте вокруг точки О на 180° фигура переходит сама в себя.
О
180°

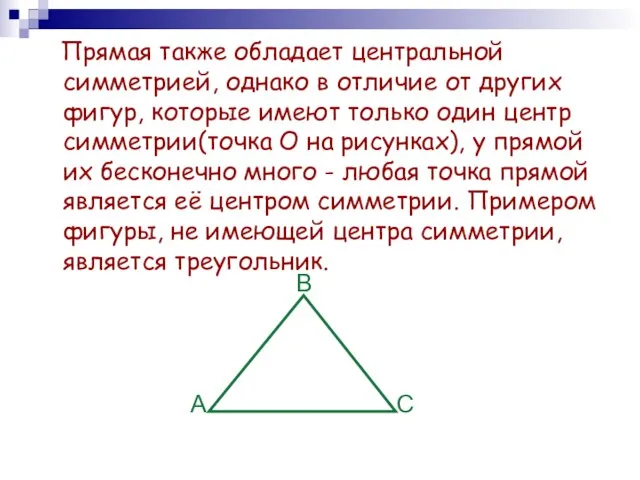
Прямая также обладает центральной симметрией, однако в отличие от других фигур, которые имеют только один центр симметрии(точка О на рисунках), у прямой их бесконечно много - любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является треугольник.
А
В
С

Применение на практике:
Примеры симметрии в растениях:
Вопрос о симметрии в растениях возник ещё в 5 веке до н. э. На явление симметрии в живой природе обратили внимание в Древней Греции пифагорейцы в связи с развитием ими учения о гармонии. В 19 веке появлялись отдельные работы, касающиеся этой темы. А в 1961 году как результат многовековых исследований, посвященных поиску красоты и гармонии окружающей нас природы, появилась наука биосимметрика.
Центральная симметрия характерна для различных плодов: голубика, черника, вишня, клюква. Рассмотрим разрез любой из этих ягод. В разрезе она представляет собой окружность, а окружность, как нам известно, имеет центр симметрии.
Центральную симметрию можно наблюдать на изображении таких цветов как цветок одуванчика, цветок мать-и-мачехи, цветок кувшинки, сердцевина ромашки, а в некоторых случаях центральной симметрией обладает и изображение всего цветка ромашки. Её сердцевина представляет собой окружность, и поэтому центрально симметрична, так как мы знаем, что окружность имеет центр симметрии. Весь же цветок обладает центральной симметрией только в случае четного количества лепестков. В случае же нечетного количества лепестков, вспомните анютины глазки , он обладает только осевой.
Выводы:
По нашим наблюдениям, в любом растении можно найти какую-то его часть, обладающую осевой или центральной симметрией. Это могут быть листья, цветы, стебли, стволы деревьев, плоды, и более мелкие части, такие как сердцевина цветка, пестик, тычинки и другие.
Осевая симметрия присуща различным видам растений и грибам, и их частям.
Центральная симметрия наиболее характерна для плодов растений и некоторых цветов.

Ромашка
Анютины глазки

Центральная симметрия в архитектуре:
Во второй половине XVIII - первой трети XIX века Петербург приобрёл воспетый А.С. Пушкиным “строгий, стройный вид”, который придала городу архитектура классицизма. Все здания, построенные в стиле классицизм, имеют четкие прямолинейные симметричные композиции. В начале XIX века по проекту А.Н. Воронихина было сооружено выдающееся произведение искусства – Казанский собор. Перед Казанским собором симметрично установлены памятники М.И. Кутузову и М.Б. Барклаю-де-Толли, полководцам, разгромившим армию Наполеона.
Примером современных зданий, построенных в середине ХХ века, является гостиница “Прибалтийская”. Симметричность, как видно из чертежа присутствует как в общей композиции, так и в каждой из трех его составляющих:средняя часть – арка с куполом и пикой на вершине, два боковых крыла гостиницы.
Выводы:
Принципы симметрии являются основополагающими для любого архитектора, но вопрос о соотношении между симметрией и асимметрией каждый архитектор решает по-разному. Асимметричное в целом сооружение может являть собой гармоническую композицию симметричных элементов.
Удачное решение определяется талантом зодчего, его художественным вкусом и его пониманием прекрасного. Прогуляйтесь по нашему городу и убедитесь, что удачных решений может быть очень много, но неизменным остается одно – стремление архитектора к гармонии, а это в той или иной степени связано с симметрией.

Гостиница «Прибалтийская»
Казанский собор

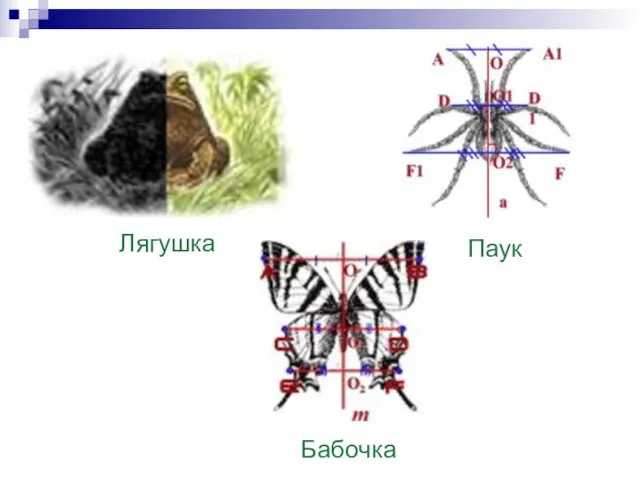
Центральная симметрия в зоологии:
Рассмотрим, как связаны животный мир и симметрия. Центральная симметрия наиболее характерна для животных, ведущих подводный образ жизни.
А также есть пример асимметричных животных: инфузория-туфелька и амёба
Выводы:
Симметрию живого существа определяет направление его движения. Для живых существ, для которых ведущим направлением является направление движения “вперед”, наиболее характерна осевая симметрия. Так как в этом направлении животные устремляются за пищей и в этом же спасаются от преследователей. А нарушение симметрии привело бы к торможению одной из сторон и превращению поступательного движения в круговое.
Центральная симметрия чаще встречается в форме животных, обитающих под водой.
Асимметрию можно наблюдать на примере простейших животных.

Лягушка
Паук
Бабочка

инфузория-туфелька и амёба

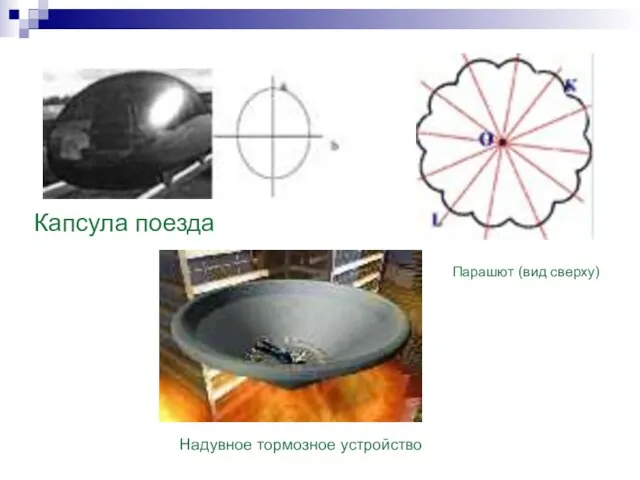
Центральная симметрия в транспорте:
Центральная симметрия не совместима с формой наземного и подземного транспорта. Причиной этого служит его направление движения. При рассмотрении вида сверху трамвая, электровоза, телеги, мы видим, что ось симметрии проходит вдоль направления движения. Таким образом, центральную симметрию следует искать в воздушном и подводном транспорте, т. е. в таких видах, где направления: вперед, назад, вправо, влево, – равноценны.
Один из таких видов транспорта – это воздушный шар.
Другой пример воздушного транспорта – это парашют. Ученые относят его изобретение еще к 13 веку. На нашем чертеже мы представили вид сверху воздушного шара. Отметим, что он аналогичен виду сверху парашюта. Как мы видим, эта фигура центрально симметрична. О – центр симметрии.
Дальнейшее развитие парашют получил в изобретении нашими учеными “надувного тормозного устройства”. Оно предназначено для спуска грузов и человека с орбиты. Надувное тормозное устройство представляет собой эластичную оболочку, наполняемую в космосе. Она имеет гибкую теплозащиту и дополнительную надувную оболочку. На базе него предполагается конструирование и спасательных устройств, которые могут использоваться, например, при пожаре в многоэтажных домах. Вид сверху этого устройства представляет собой круг. А круг, как мы знаем, не только обладает осевой симметрией, но и центральной. Центр симметрии совпадает с центром круга.
Выводы:
Вид сверху и вид спереди различных видов транспорта обладает либо центральной, либо осевой симметрией.
Для наземного вида транспорта в большей степени характерна осевая симметрия. Причиной этого является направление его движения.
Центральная симметрия чаще встречается в форме воздушного и подводного транспорта, для которого направления: вправо, влево, вперед, назад, – равноценны.
Модели транспорта будущего в той же степени, что и модели настоящего и прошлого обладают различными видами.

Надувное тормозное устройство
Капсула поезда
Парашют (вид сверху)

А также с симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту. В большинстве случаев симметричны относительно центра узоры на коврах, тканях, комнатных обоях.
Симметричны многие детали механизмов, например зубчатые колёса.

Аксиомы стереометрии и планиметрии
Подготовила: ученица Х «А» класса Зацепина Екатерина.

Аксиомы стереометрии.

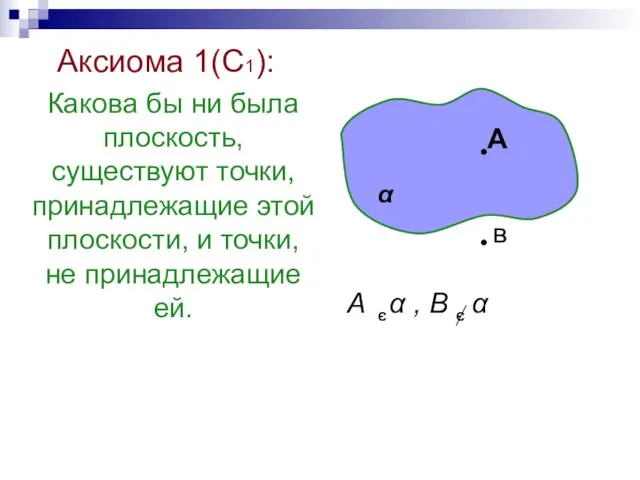
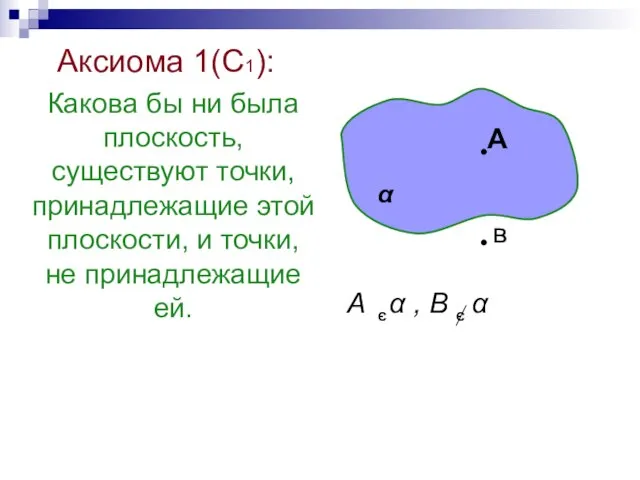
Аксиома 1(С1):
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
А α , В α
α
Α
в
Э
Э

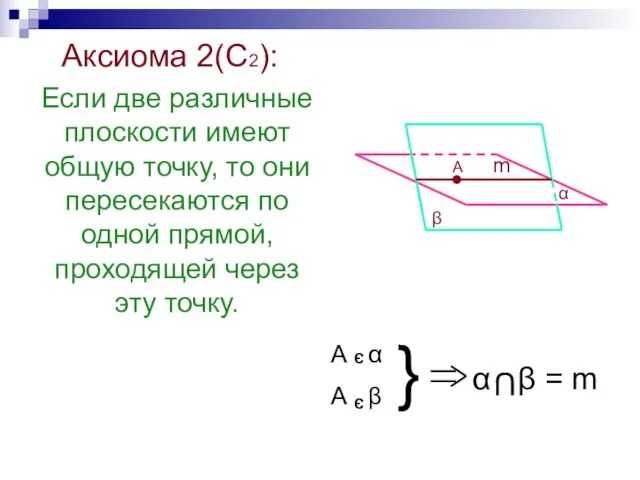
Аксиома 2(С2):
Если две различные плоскости имеют общую точку, то они пересекаются по одной прямой, проходящей через эту точку.
β
α
А α
А β
Э
Э
}
α β = m
U
m
А

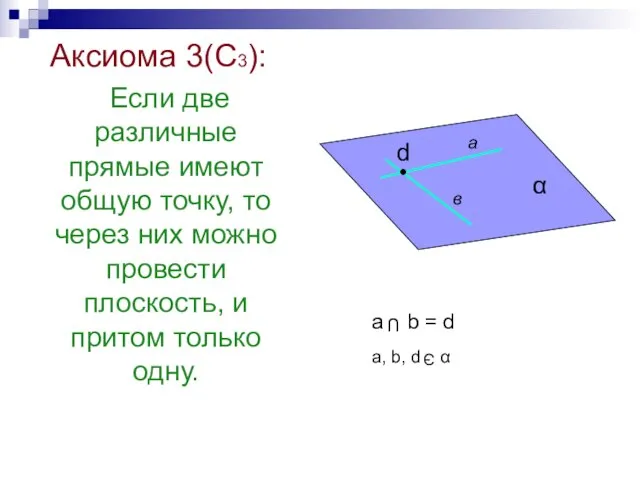
Аксиома 3(С3):
Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
a b = d
a, b, d α
U
Э
d
α
в
a

Аксиомы планиметрии.

Аксиома I:
Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
А α , В α
Э
Э
А
В
А,В=α
α
α
А
В

Аксиома II:
Из трёх точек на прямой одна и только одна лежит между двумя другими.
А
В
С

Аксиома III:
Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
А
В
АВ > 0

Аксиома III:
Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
А
В
АC + CВ > 0
C

Аксиома III:
Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
А
В
АC+CВ > 0
C

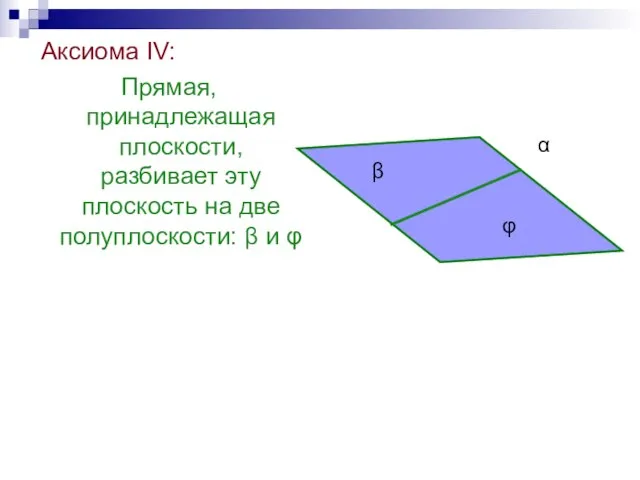
Аксиома IV:
Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости: β и φ
β
α
φ

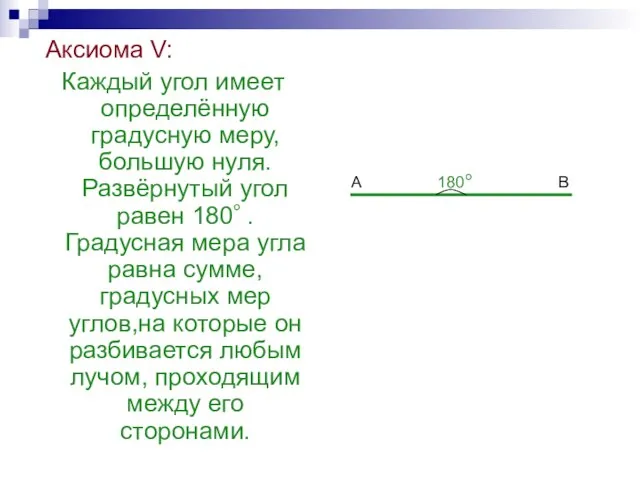
Аксиома V:
Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180 . Градусная мера угла равна сумме, градусных мер углов,на которые он разбивается любым лучом, проходящим между его сторонами.
180
В
А

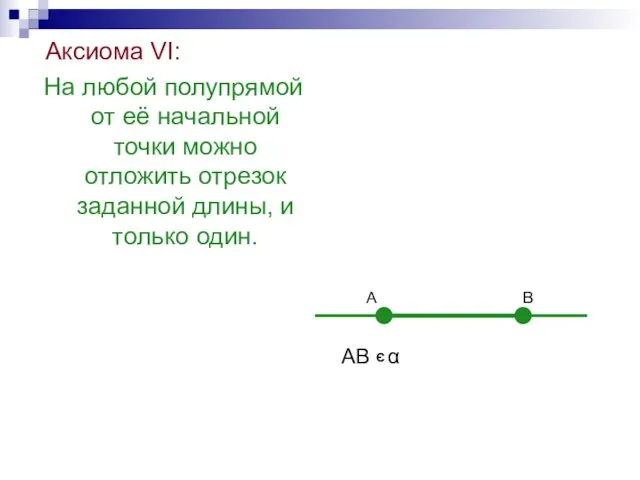
Аксиома VI:
На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один.
А
В
АВ α
Э

Аксиома VII:
От полупрямой на содержащей её плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180, и только один. φ = 45°< 180°
α
b
φ=45°

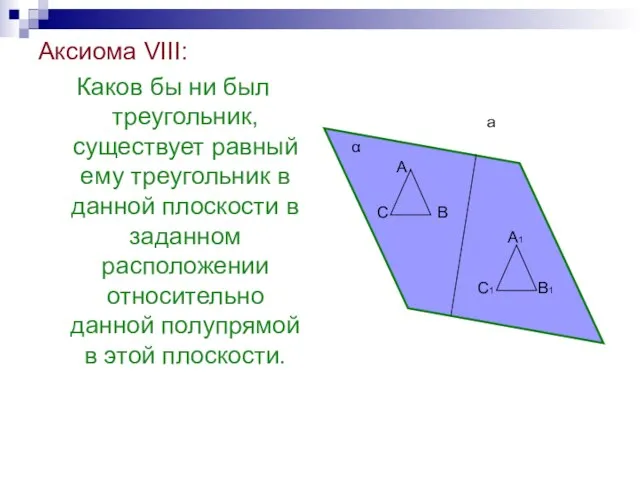
Аксиома VIII:
Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
α
а
А
В
С
А1
В1
С1

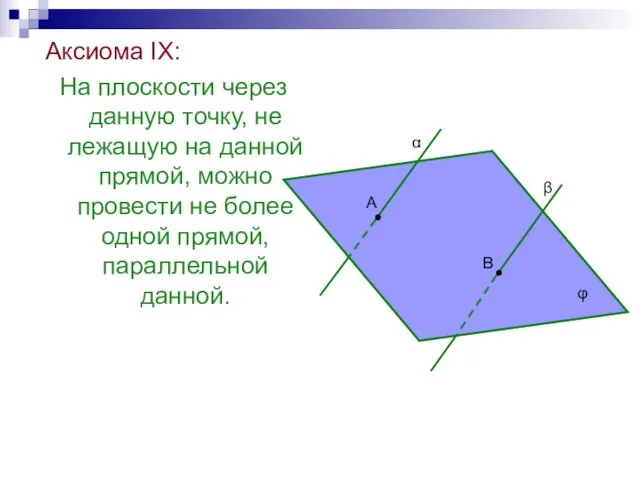
Аксиома IX:
На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
А
α
β
φ
B

Аксиома 1(С1):
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
А α , В α
α
Α
в
Э
Э