Цилиндр, конус и шар

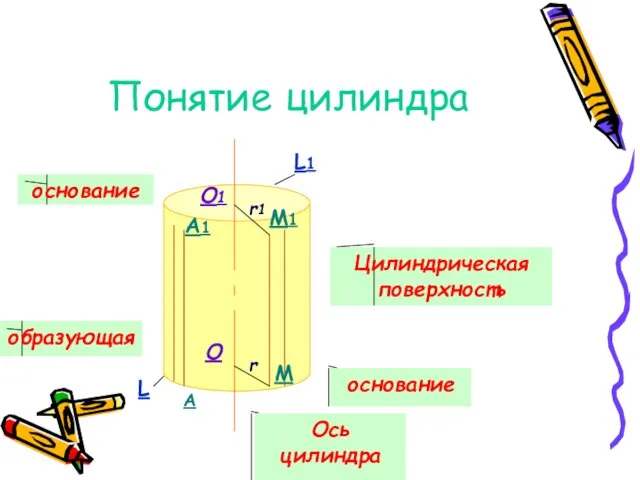
Понятие цилиндра
основание
образующая
основание
Цилиндрическая
поверхность
Ось
цилиндра
О1
О
r1
r
M
M1
A
A1
L1
L

Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1, называется цилиндром.
Цилиндрическая поверхность – боковая поверхность
цилиндра, а круги –
основания цилиндра
Образующие цилиндрической поверхности – образующие
цилиндра, а
прямая ОО1 – ось цилиндра
(все образующие параллельны и равны)
Длина образующей – высота цилиндра, а радиус основания –
радиус цилиндра
Запомни это !
Основные понятия

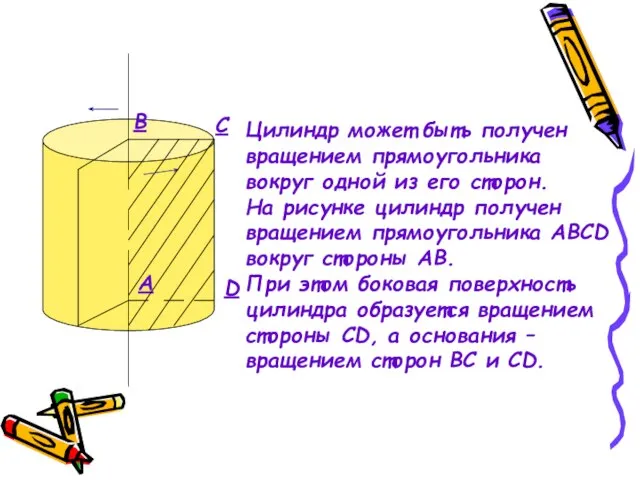
B
C
D
A
Цилиндр может быть получен
вращением прямоугольника
вокруг одной из его сторон.
На рисунке цилиндр получен
вращением прямоугольника АBCD
вокруг стороны AB.
При этом боковая поверхность
цилиндра образуется вращением
стороны CD, а основания –
вращением сторон BC и CD.

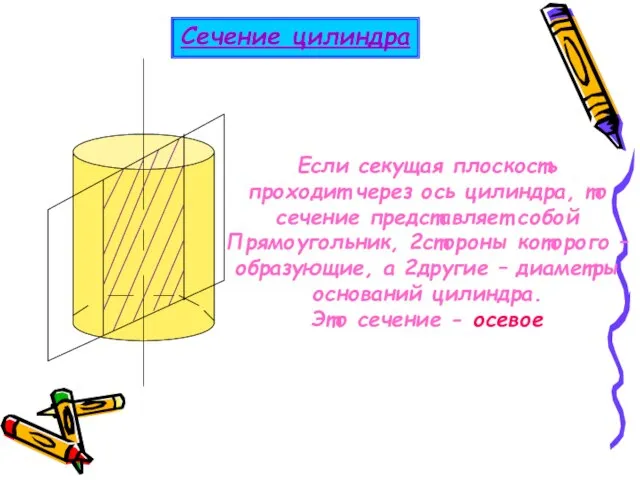
Если секущая плоскость
проходит через ось цилиндра, то
сечение представляет собой
Прямоугольник, 2стороны которого –
образующие, а 2другие – диаметры
оснований цилиндра.
Это сечение - осевое
Сечение цилиндра

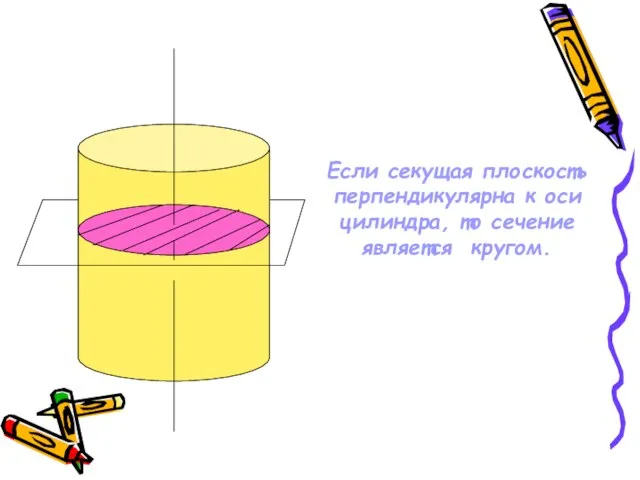
Если секущая плоскость
перпендикулярна к оси
цилиндра, то сечение
является кругом.

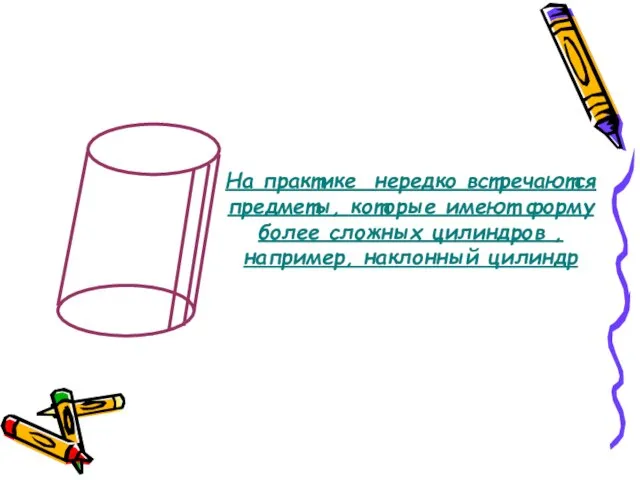
На практике нередко встречаются
предметы, которые имеют форму
более сложных цилиндров ,
например, наклонный цилиндр

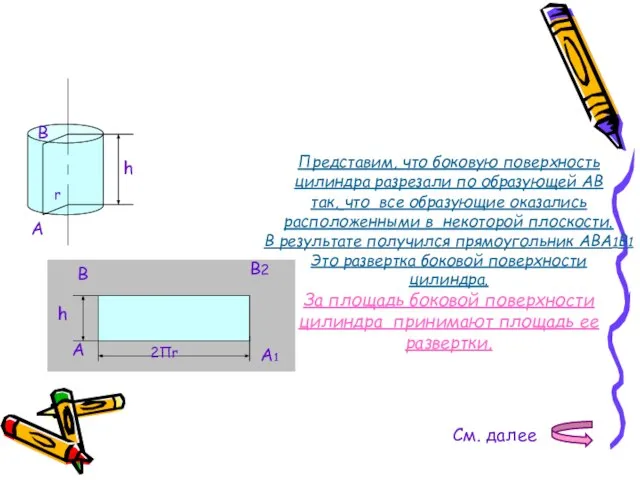
Площадь поверхности цилиндра
A
B
r
h
A
B
A1
B2
h
2Пr
Представим, что боковую поверхность
цилиндра разрезали по образующей AB
так, что все образующие оказались
расположенными в некоторой плоскости.
В результате получился прямоугольник ABA1B1
Это развертка боковой поверхности
цилиндра.
За площадь боковой поверхности
цилиндра принимают площадь ее
развертки.
См. далее

Основание AA1 прямоугольника является разверткой
окружности основания цилиндра, а высота AB –
образующей цилиндра, поэтому
AA1= 2Пr ; AB=h,
где r- радиус цилиндра, h- высота.
Так как площадь прямоуг.
ABA1B1 = AA1 * AB = 2Пrh,
то
Sбок=2Пrh
Площадь боковой поверхности цилиндра равна
произведению длины окружности основания
на высоту цилиндра.
Площадь полной поверхности цилиндра = сумме площадей
боковой поверхности и двух оснований
Sцил= 2Пrh +2Пr*r=2Пr (r + h)

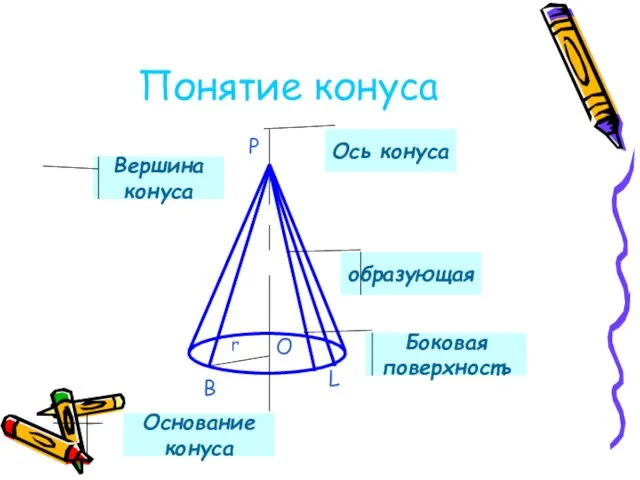
Понятие конуса
B
P
O
r
L
Ось конуса
Вершина конуса
образующая
Боковая поверхность
Основание конуса

Основные понятия
Тело, ограниченное конической поверхностью и кругом
с границей L, называется конусом
Коническая поверхность – боковая поверхность конуса, а
круг – основание конуса
Точка Р- вершина конуса, а образующие конической поверхности-
-образующие конуса.
Прямая ОР, проходящая через центр основания и вершину,
называется осью конуса.
Ось конуса перпендикулярна к плоскости основания.
Отрезок ОР- высота конуса.

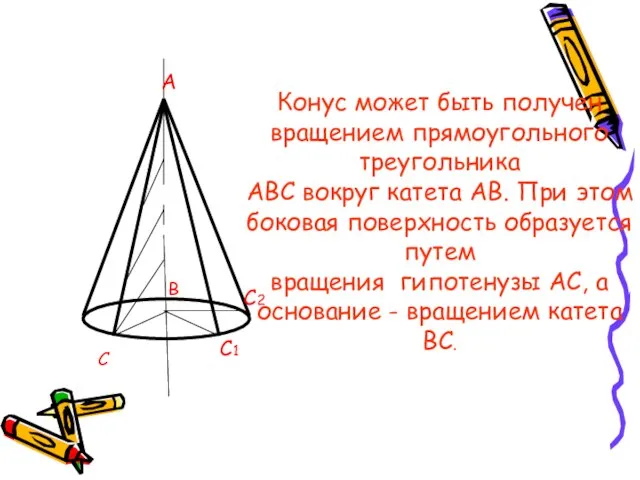
С
С2
С1
В
А
Конус может быть получен
вращением прямоугольного треугольника
АВС вокруг катета АВ. При этом
боковая поверхность образуется путем
вращения гипотенузы АС, а
основание - вращением катета ВС.

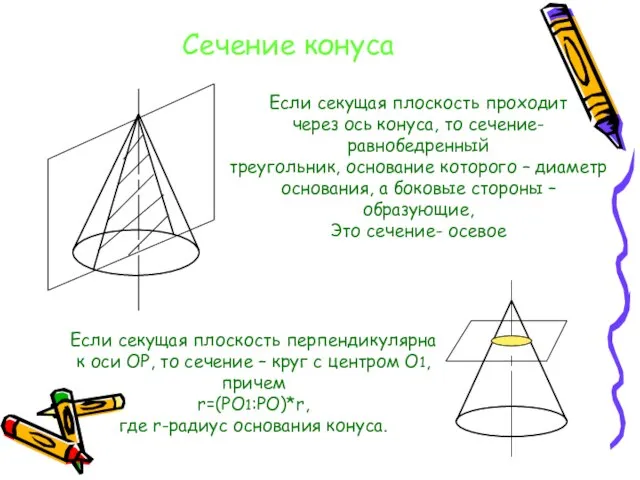
Сечение конуса
Если секущая плоскость проходит
через ось конуса, то сечение- равнобедренный
треугольник, основание которого – диаметр
основания, а боковые стороны – образующие,
Это сечение- осевое
Если секущая плоскость перпендикулярна
к оси ОР, то сечение – круг с центром О1,
причем
r=(РО1:РО)*r,
где r-радиус основания конуса.

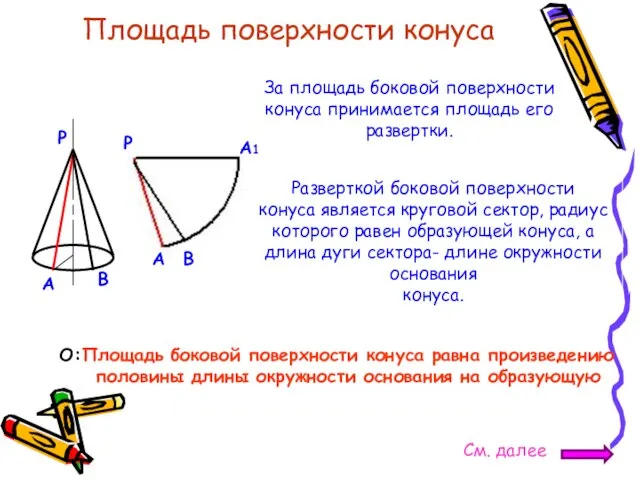
Площадь поверхности конуса
За площадь боковой поверхности
конуса принимается площадь его
развертки.
Разверткой боковой поверхности
конуса является круговой сектор, радиус
которого равен образующей конуса, а
длина дуги сектора- длине окружности основания
конуса.
См. далее
P
A
B
P
A
A1
B
Площадь боковой поверхности конуса равна произведению
половины длины окружности основания на образующую
О:

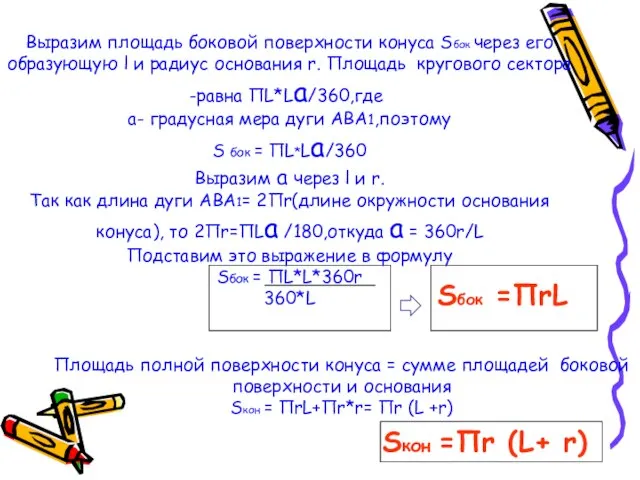
Выразим площадь боковой поверхности конуса Sбок через его
образующую l и радиус основания r. Площадь кругового сектора
равна ПL*La/360,где
a- градусная мера дуги ABA1,поэтому
S бок = ПL*La/360
Выразим a через l и r.
Так как длина дуги ABA1= 2Пr(длине окружности основания конуса), то 2Пr=ПLa /180,откуда a = 360r/L
Подставим это выражение в формулу
Sбок = ПL*L*360r
360*L
Sбок =ПrL
Площадь полной поверхности конуса = сумме площадей боковой
поверхности и основания
Sкон = ПrL+Пr*r= Пr (L +r)
Sкон =Пr (L+ r)

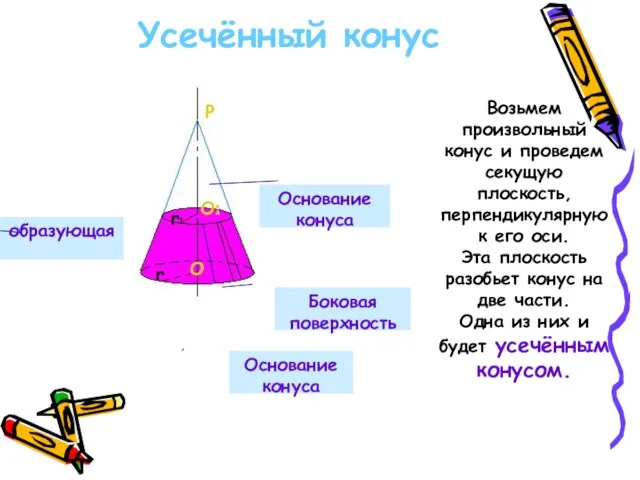
Усечённый конус
P
O
O1
r
r1
Основание конуса
Основание конуса
образующая
Боковая поверхность
Возьмем произвольный конус и проведем секущую плоскость, перпендикулярную к его оси.
Эта плоскость разобьет конус на две части.
Одна из них и будет усечённым конусом.

Основные понятия
Основание исходного конуса и круг, полученный в сечении этого
конуса плоскостью- основания усечённого конуса, а отрезок,
соединяющий их центры- высота
Часть конической поверхности, ограничивающая усечённый конус-
его боковая поверхность, а отрезки образующих конической поверхности
- образующие усечённого конуса
Это нужно выучить!

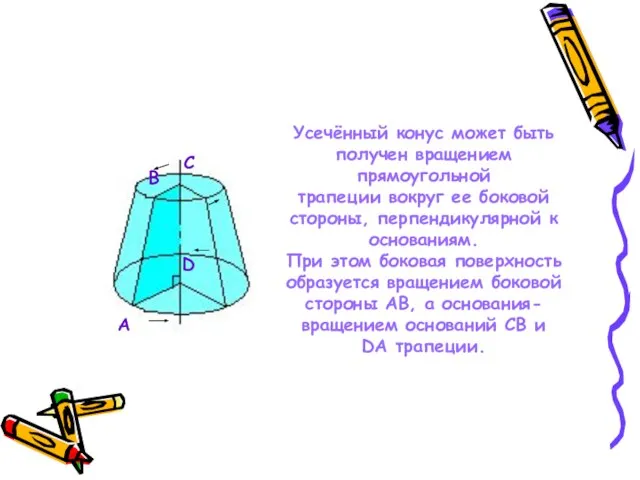
Усечённый конус может быть получен вращением прямоугольной
трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.
При этом боковая поверхность образуется вращением боковой стороны AB, а основания- вращением оснований CB и DA трапеции.
A
B
C
D

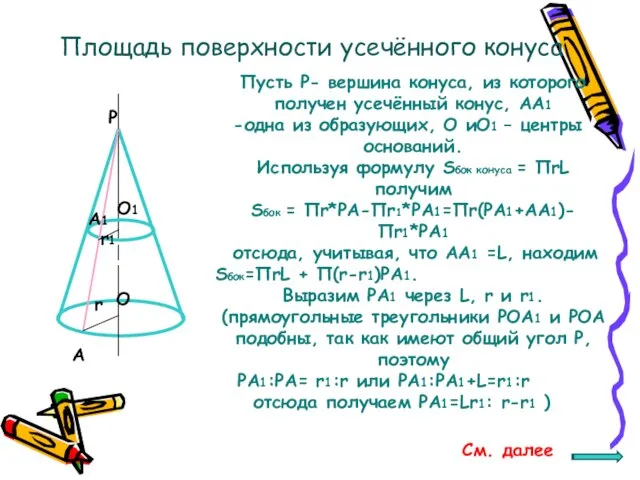
Площадь поверхности усечённого конуса
Пусть P- вершина конуса, из которого получен усечённый конус, AA1
одна из образующих, О иО1 – центры оснований.
Используя формулу Sбок конуса = ПrL получим
Sбок = Пr*PA-Пr1*PA1=Пr(PA1+AA1)- Пr1*PA1
отсюда, учитывая, что AA1 =L, находим
Sбок=ПrL + П(r-r1)PA1.
Выразим PA1 через L, r и r1. (прямоугольные треугольники POA1 и POA подобны, так как имеют общий угол Р, поэтому
РА1:РА= r1:r или РА1:РА1+L=r1:r отсюда получаем РА1=Lr1: r-r1 )
См. далее
Р
А
А1
О
О1
r
r1

Подставим это выражение в формулу
Sбок= ПrL+ П(r-r1)PA1,
получим
ПrL + П(r-r1)*Lr1
r-r1
= ПrL+ Пr1L=П(r+r1)L
Sбок= П(r+r1)L
Площадь боковой поверхности усечённого конуса
равна произведению полусуммы длин окружностей оснований на образующую
О:

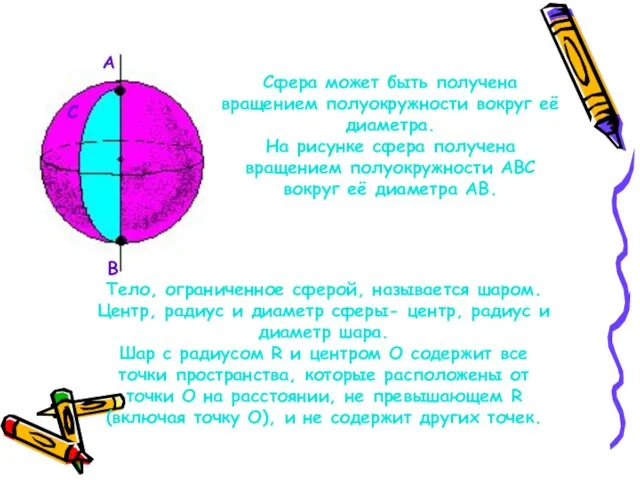
Сфера и шар
R
O
Сферой называется поверхность,
состоящая из всех точек пространства, которые расположены на данном расстоянии от данной точки.
Данная точка – центр сферы, а данное расстояние-
-радиус сферы.
Любой отрезок, соединяющий центр и какую-нибудь точку сферы,
также является радиусом. Отрезок, соединяющий две точки сферы
и проходящий через её центр- диаметр(=2R)

А
В
С
Сфера может быть получена вращением полуокружности вокруг её диаметра.
На рисунке сфера получена вращением полуокружности АВС вокруг её диаметра АВ.
Тело, ограниченное сферой, называется шаром.
Центр, радиус и диаметр сферы- центр, радиус и диаметр шара.
Шар с радиусом R и центром О содержит все точки пространства, которые расположены от точки О на расстоянии, не превышающем R (включая точку О), и не содержит других точек.

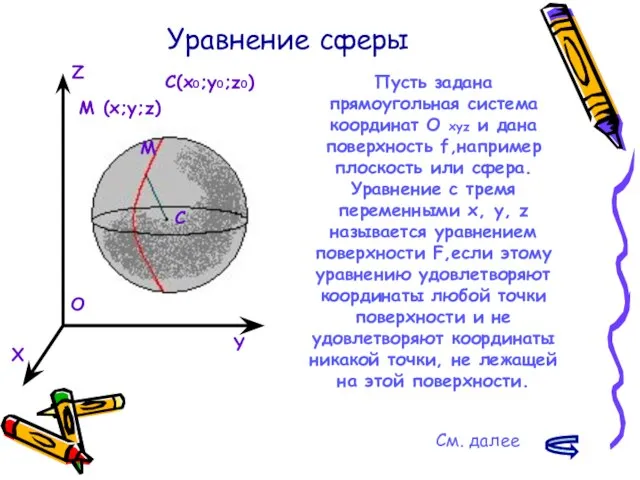
Уравнение сферы
Y
X
Z
O
C
M
C(x0;y0;z0)
M (x;y;z)
Пусть задана прямоугольная система координат O xyz и дана поверхность f,например плоскость или сфера.
Уравнение с тремя переменными x, y, z называется уравнением поверхности F,если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.
См. далее

Выведем уравнение сферы радиуса R с центром С(x0;y0;z0)
Расстояние от произвольной точки М(x;y;z)до точки С вычисляется по формуле:
2 2 2
МС= (x-x0)+(y-y0)+(z-z0)
2 2
Если точка М лежит на данной сфере, то М=R, т.е. МС=R,
то есть координаты точки М удовлетворяют уравнению
2 2 2 2
(x-x0)+(y-y0)+(z-z0)=R
Если же точка М не лежит на данной сфере, то МС=R,
т. е. координаты точки М не удовлетворяют первому уравнению.
В прямоугольной системе координат уравнение сферы радиуса R с центром С(x;y;z) имеет вид
2 2 2 2
(x-x0)+(y-y0)+(z-z0)=R

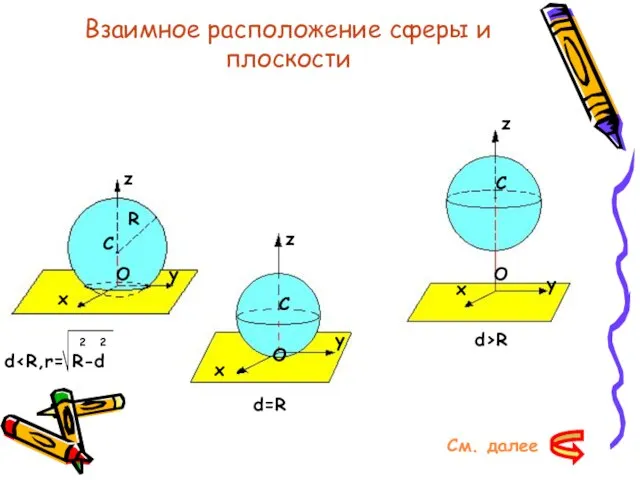
Взаимное расположение сферы и плоскости
z
y
x
O
C
R
y
x
z
C
z
y
x
C
O
O
2 2
d
d=R
d>R
См. далее

Обозначим радиус сферы –R, а расстояние от её центра до плоскости – d.
Введем систему координат :плоскость Оxy совпадает с плоскостью, а центр С сферы лежит на положительной полуосиOz.
В этой системе С имеет координаты (0;0; d),поэтому сфера имеет уравнение
2 2 2 2
x +y +(z -d)=R
Плоскость а совпадёт с плоскостью Oxy, значит z=0.
Вопрос о взаимном расположении сферы и плоскости сводится к исследованию системы уравнений:
z=0
2 2 2 2
x +y +( z- d)=R
Подставив z=0 во второе уравнение получим:
2 2 2 2
x +y=R- d.

Возможны три случая:
1.d
R-d>0,
и уравнение окружности радиуса 2 2
r = R-d
с центром в точке О на плоскости Oxy.В данном случае сфера и плоскость пересекаются по окружности.
Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы- окружность
2.d=R,тогда 2 2
R-d=0,
И ур-нию удовлетворяют значения x=0,y=0.Значит О(0;0;0),то есть
Если расстояние от центра сферы до плоскости равно радиусу сферы0
то сфера и плоскость имеют только одну общую точку.
3.d>R,тогда 2 2
R-d<0,
И уравнению не удовлетворяют координаты никакой точки.
Если расстояние от центра до плоскости больше радиуса сферы,
то сфера и плоскость не имеют общих точек.

Касательная плоскость к сфере
А
О
Плоскость., имеющая со сферой одну общую точку, называется касательной плоскостью к сфере, а их общая точка- точка касания плоскости и сферы.
На рисунке плоскость а- касательная плоскость к сфере с центром О,
а А-точка касания.
а
См. далее

Свойство касательной плоскости:
Т: радиус сферы, проведенный в точку касания, перпендикулярен к касательной плоскости.
Доказательство:
Рассмотрим рисунок, показанный ранее. Предположим, что радиус
не перпендикулярен к плоскости. Тогда он является наклонной к плоскости а, то есть расстояние от сферы до плоскости меньше радиуса сферы, то есть они пересекаются по окружности, а это невозможно, так как а- касательная. Значит радиус перпендикулярен к плоскости, ч. т. д.
Обратная теорема: если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость- касательная к сфере
Доказательство:
Из условия следует, что радиус- перпендикуляр, проведённый из центра сферы к плоскости. Значит, расстояние от центра сферы до плоскости = радиусу, сфера и плоскость имеют одну общую точку, то есть данная плоскость- касательная к сфере, ч. т. д.

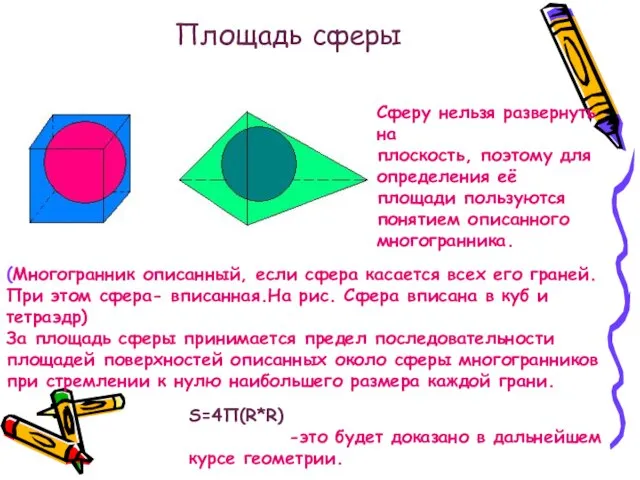
Площадь сферы
Сферу нельзя развернуть на
плоскость, поэтому для определения её площади пользуются понятием описанного многогранника.
(Многогранник описанный, если сфера касается всех его граней.
При этом сфера- вписанная.На рис. Сфера вписана в куб и тетраэдр)
За площадь сферы принимается предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани.
S=4П(R*R)
-это будет доказано в дальнейшем курсе геометрии.