Дефекты в кристаллах

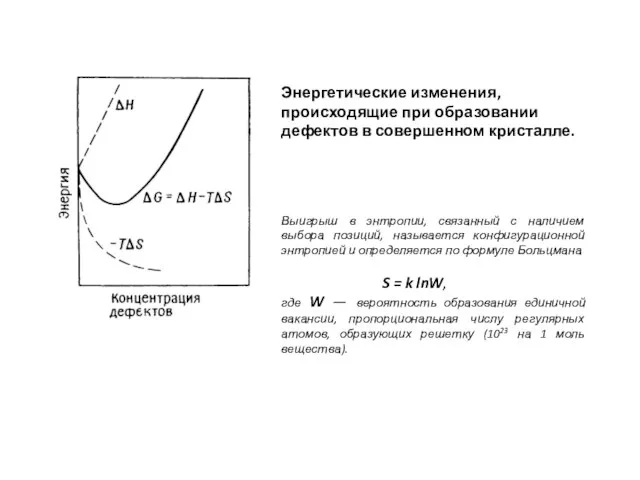
Энергетические изменения, происходящие при образовании дефектов в совершенном кристалле.
Выигрыш в энтропии, связанный с наличием выбора позиций, называется конфигурационной энтропией и определяется по формуле Больцмана
S = k lnW,
где W — вероятность образования единичной вакансии, пропорциональная числу регулярных атомов, образующих решетку (1023 на 1 моль вещества).

Классификация дефектов по виду разупорядочения.

Типы доминирующих точечных дефектов в различных кристаллах

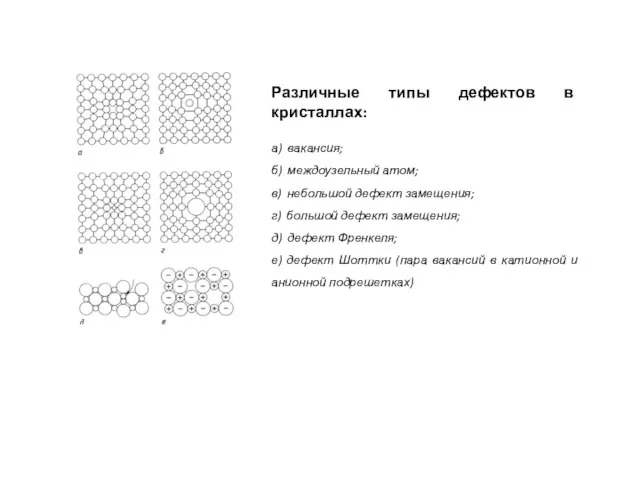
Различные типы дефектов в кристаллах:
а) вакансия;
б) междоузельный атом;
в) небольшой дефект замещения;
г) большой дефект замещения;
д) дефект Френкеля;
е) дефект Шоттки (пара вакансий в катионной и анионной подрешетках)

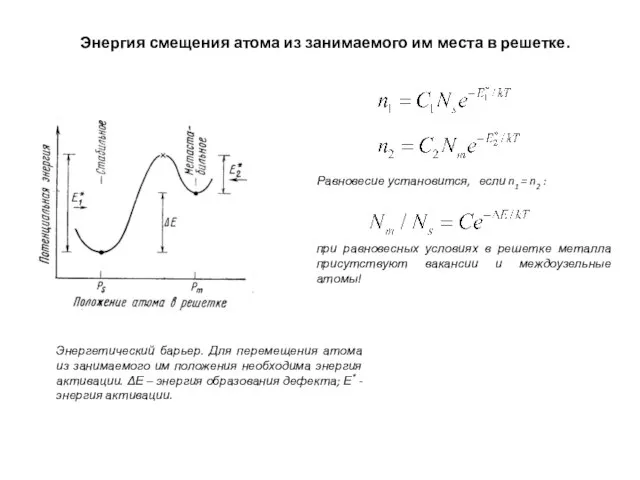
Энергия смещения атома из занимаемого им места в решетке.
Энергетический барьер. Для перемещения атома из занимаемого им положения необходима энергия активации. ΔЕ – энергия образования дефекта; Е* - энергия активации.
,
Равновесие установится, если n1 = n2 :
при равновесных условиях в решетке металла присутствуют вакансии и междоузельные атомы!

Дислокации.
Механические свойства и реакционная способность твердых тел.
- металлы оказываются обычно гораздо пластичнее, чем это можно ожидать на основе расчетов. Расчетная величина напряжений сдвига в металлах составляет 105 - 106 Н/см2 , тогда как экспериментально найденные значения на многих металлах не превышают 10 - 100 Н/см2. Это указывает на то, что в структуре металлов имеются некие «слабые звенья», благодаря которым металлы деформируются столь легко;
2) - на поверхностях многих кристаллов с хорошей огранкой под микроскопом или даже невооруженным глазом заметны спирали, по которым проходил рост кристалла. Такие спирали не могут образовываться в совершенных кристаллах;
3) - без представлений о существовании дислокаций было бы трудно объяснить такие свойства металлов, как пластичность и текучесть. Пластинки металлического магния, например, могут быть, почти как резина, растянуты в несколько раз по сравнению с первоначальной длиной;
4) - наклеп в металлах не удавалось объяснить без привлечения представлений о дислокациях.

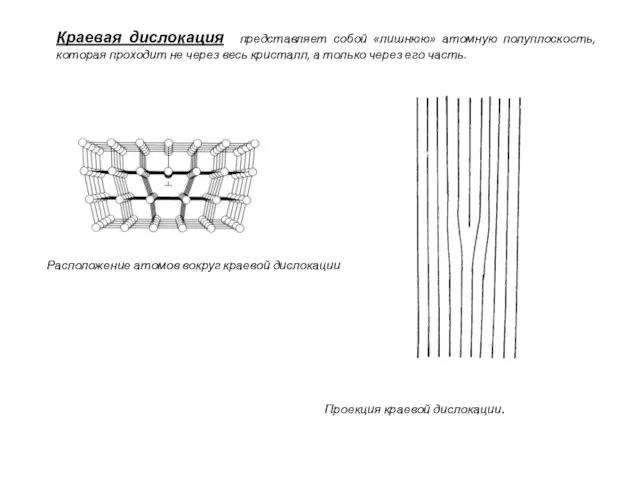
Расположение атомов вокруг краевой дислокации
Краевая дислокация представляет собой «лишнюю» атомную полуплоскость, которая проходит не через весь кристалл, а только через его часть.
Проекция краевой дислокации.

Перемещение краевой дислокации под действием сдвигового напряжения.
Если соединить точки А и В , то это будет проекция плоскости скольжения, вдоль которой перемещаются дислокации.
Дислокации характеризуются вектором Бюргерса b. Для нахождения величины и направления b надо описать вокруг дислокации контур, мысленно проводя его от атома к атому (рис. д). В бездефектной области кристалла такой контур ABCD, построенный из трансляций на одно межатомное расстояние в каждом направлении, замкнут: начало и конец его совпадают в точке А. Напротив, контур 12345, окружающий дислокацию, незамкнут, так как точки 1 и 5 не совпадают. Величина вектора Бюргерса равна расстоянию 1 - 5, а направление тождественно направлению 1 - 5 (или 5 - 1). Вектор Бюргерса краевой дислокации перпендикулярен линии дислокации и параллелен направлению движения линии дислокации (или направлению сдвига) под действием приложенного напряжения.

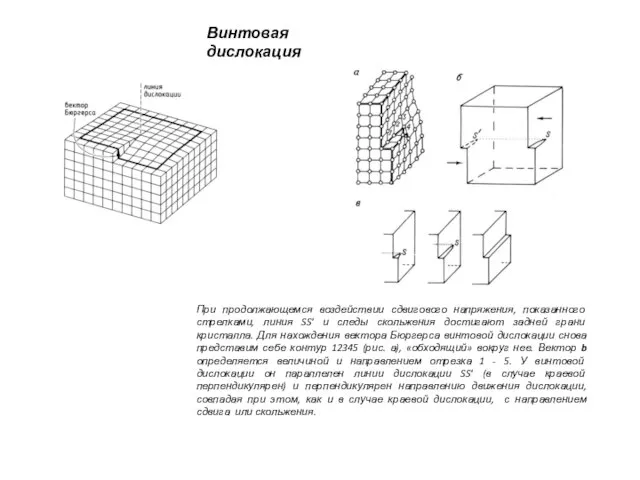
Винтовая дислокация
При продолжающемся воздействии сдвигового напряжения, показанного стрелками, линия SS' и следы скольжения достигают задней грани кристалла. Для нахождения вектора Бюргерса винтовой дислокации снова представим себе контур 12345 (рис. а), «обходящий» вокруг нее. Вектор b определяется величиной и направлением отрезка 1 - 5. У винтовой дислокации он параллелен линии дислокации SS' (в случае краевой перпендикулярен) и перпендикулярен направлению движения дислокации, совпадая при этом, как и в случае краевой дислокации, с направлением сдвига или скольжения.

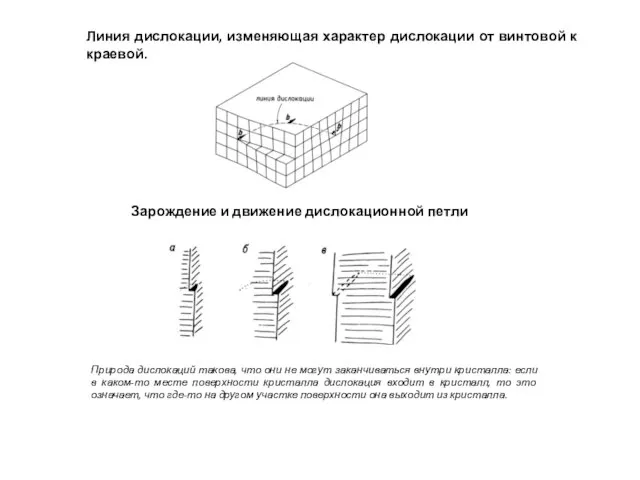
Линия дислокации, изменяющая характер дислокации от винтовой к краевой.
Зарождение и движение дислокационной петли
Природа дислокаций такова, что они не могут заканчиваться внутри кристалла: если в каком-то месте поверхности кристалла дислокация входит в кристалл, то это означает, что где-то на другом участке поверхности она выходит из кристалла.

Схема возникновения дислокационной петли (кольца)
Схемы возникновения вакансий (б) путем аннигиляции двух дислокаций противоположного знака (а).
В действительности прямое приложение внешней деформирующей силы для образования дислокаций не обязательно. Такой силой могут быть термические напряжения, возникающие при кристаллизации, или, например, аналогичные напряжения в области посторонних включений в затвердевающем металлическом слитке при охлаждении расплава и др. В реальных кристаллах лишние экстраплоскости могут возникать одновременно в разных частях кристалла. Экстраплоскость, а значит и дислокации подвижны в кристалле. В этом состоит их первая важная особенность.
Вторая особенность дислокаций состоит в их взаимодействии с образованием новых дислокаций, дислокационных петель, аналогичных тем, что показаны на рисунках, представленных ниже, и даже с образованием вакансий за счет аннигиляции двух дислокаций противоположного знака.

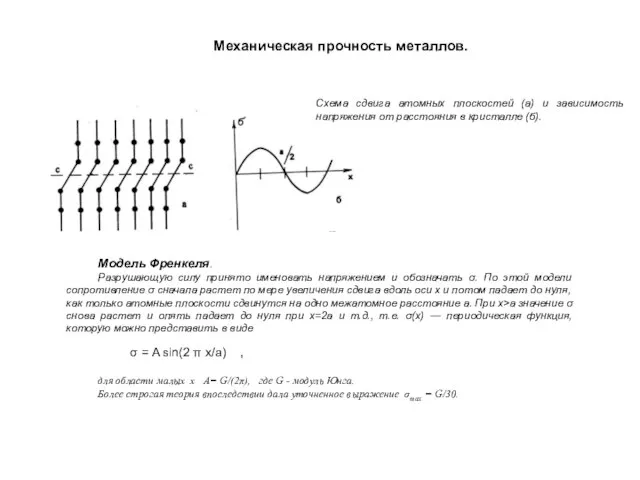
Механическая прочность металлов.
Модель Френкеля.
Разрушающую силу принято именовать напряжением и обозначать σ. По этой модели сопротивление σ сначала растет по мере увеличения сдвига вдоль оси х и потом падает до нуля, как только атомные плоскости сдвинутся на одно межатомное расстояние а. При х>а значение σ снова растет и опять падает до нуля при х=2а и т.д., т.е. σ(х) — периодическая функция, которую можно представить в виде
σ = A sin(2 π х/а) ,
для области малых х A= G/(2π), где G - модуль Юнга.
Более строгая теория впоследствии дала уточненное выражение σmах = G/30.
Схема сдвига атомных плоскостей (а) и зависимость напряжения от расстояния в кристалле (б).

Экспериментальные и теоретические значения предела сдвиговой прочности некоторых металлов.
Роликовая модель сдвига атомных плоскостей кристалла
|F1 + F2|=|F4 + F5|
вся система роликов находится в равновесии. Стоит лишь слегка изменить равновесие сил слабым внешним воздействием, и верхний ряд роликов переместится. Поэтому движение дислокации, т.е. совокупности дефектных атомов, происходит при малых нагрузках.
Теория дает σmах, сдвигающее дислокацию, в виде
σmах = [2С/(1 - ν) ] ехр { - 2 πa/ [d(1- ν) ]} ,
где ν - коэффициент Пуассона (поперечная упругость), d - расстояние между плоскостями скольжения, а - период кристаллической решетки.
Полагая а = d , ν = 0,3 , получаем значения σmах в последнем столбце таблицы, откуда видно, что они гораздо ближе к экспериментальным.

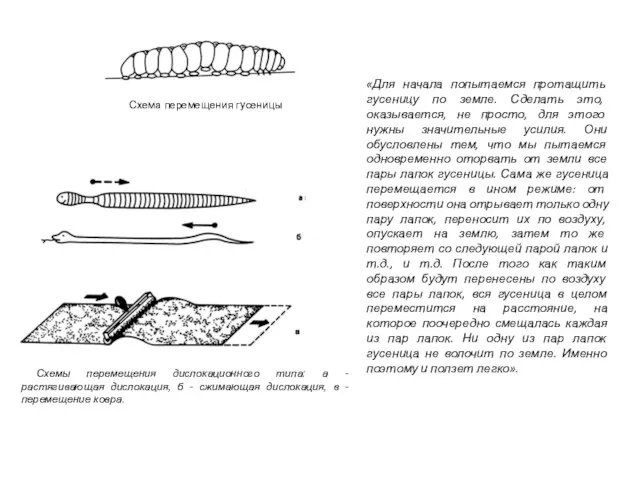
Схема перемещения гусеницы
Схемы перемещения дислокационного типа: а - растягивающая дислокация, б - сжимающая дислокация, в - перемещение ковра.
«Для начала попытаемся протащить гусеницу по земле. Сделать это, оказывается, не просто, для этого нужны значительные усилия. Они обусловлены тем, что мы пытаемся одновременно оторвать от земли все пары лапок гусеницы. Сама же гусеница перемещается в ином режиме: от поверхности она отрывает только одну пару лапок, переносит их по воздуху, опускает на землю, затем то же повторяет со следующей парой лапок и т.д., и т.д. После того как таким образом будут перенесены по воздуху все пары лапок, вся гусеница в целом переместится на расстояние, на которое поочередно смещалась каждая из пар лапок. Ни одну из пар лапок гусеница не волочит по земле. Именно поэтому и ползет легко».

Пути управления дислокационными дефектами.
Закрепление примесями. Примесный атом взаимодействует с дислокацией и перемещение такой дислокации, отягощенной примесными атомами, оказывается затрудненным. Поэтому эффективность закрепления дислокаций примесными атомами будет определяться энергией взаимодействия Е, которая в свою очередь складывается из двух составляющих: Е1 и Е2. Первая составляющая (Е1) представляет собой энергию упругого взаимодействия, а вторая (Е2) — энергию электрического взаимодействия.
Закрепление посторонними частицами. Посторонние частицы - микроскопические включения вещества, отличающегося от основного металла. Эти частицы вводятся в металлический расплав и остаются в металле после его затвердевания при охлаждении расплава. В ряде случаев эти частицы вступают в химическое взаимодействие с основным металлом, и тогда эти частицы представляют уже сплав. Механизм закрепления дислокаций такими частицами основан на различной скорости перемещения дислокаций в металлической матрице и в материале посторонних частиц.
Закрепление включениями второй фазы. Под второй фазой понимают выделение (преципитаты) избыточной по сравнению с равновесной, концентрации примеси из раствора металл - примесь. Процесс выделения называют распадом твердого раствора.
Переплетение дислокаций. При высокой плотности дислокаций в металле происходит их переплетение. Это связано с тем, что одни дислокации начинают двигаться вдоль пересекающихся плоскостей скольжения, препятствуя продвижению других.

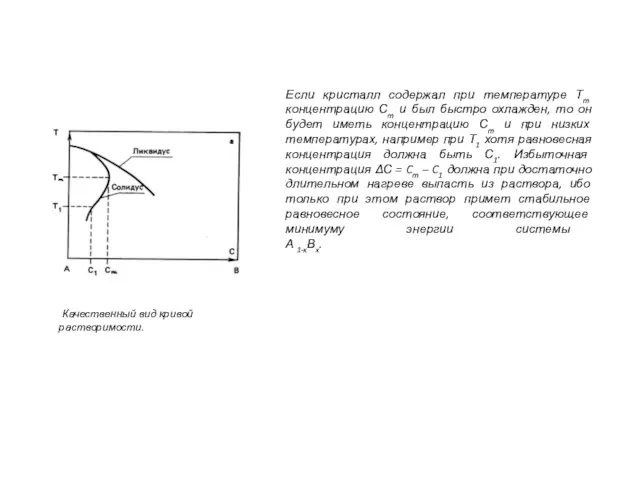
Качественный вид кривой растворимости.
Если кристалл содержал при температуре Тm концентрацию Сm и был быстро охлажден, то он будет иметь концентрацию Сm и при низких температурах, например при Т1 хотя равновесная концентрация должна быть С1. Избыточная концентрация ΔС = Cm – C1 должна при достаточно длительном нагреве выпасть из раствора, ибо только при этом раствор примет стабильное равновесное состояние, соответствующее минимуму энергии системы
А 1-xВx.

Методы обнаружения дислокаций
а) Микрофотография (получена в просвечивающем электронном микроскопе, TEM) кристалла SrTiO3, содержащего две краевые дислокации (100) (отмечены на рисунке).
б) Схематическое представление краевой дислокации.
в) Микрофотография поверхности кристалла GaAs (полученная в сканирующем туннельном микроскопе). В точке С винтовая дислокация.
г) Схема винтовой дислокации.

Визуализация дислокаций с помощью просвечивающего электронного микроскопа.
а) Темные линии на ярком фоне – линии дислокации в алюминии после 1% растяжения.
б) Причина контраста области дислокации - искривление кристаллографических плоскостей приводит к дифракции электронов, что ослабляет прошедший электронный луч

а) Ямки травления на поверхности {111} изогнутой меди;
б) на поверхности {100}
в) {110} рекристаллизованного
Al-0,5 % Mn
Дислокации можно сделать видимыми и в обычном оптическом микроскопе. Поскольку области вокруг точки выхода дислокаций на поверхность больше подвержены химическому травлению, на поверхности образуются так называемые ямки травления, которые хорошо видны в оптическом микроскопе . Их форма зависит от индексов Миллера поверхности.

Для получения металлического материала с повышенной прочностью необходимо создать большое количество центров закрепления дислокаций, причем такие центры должны быть распределены равномерно. Эти требования привели к созданию суперсплавов.
Новые металлические функциональные материалы.
«Конструирование» структуры сплавов
Суперсплав представляет собой по крайней мере двухфазную систему, в которой обе фазы отличаются в первую очередь степенью порядка в атомной структуре.
Суперсплав существует в системе Ni — Al. В этой системе может образовываться обычная смесь, т.е. сплав с хаотическим распределением атомов Ni и Аl . Этот сплав имеет кубическую структуру, но узлы куба замещаются атомами Ni или Аl , беспорядочно. Этот неупорядоченный сплав называют γ - фазой.

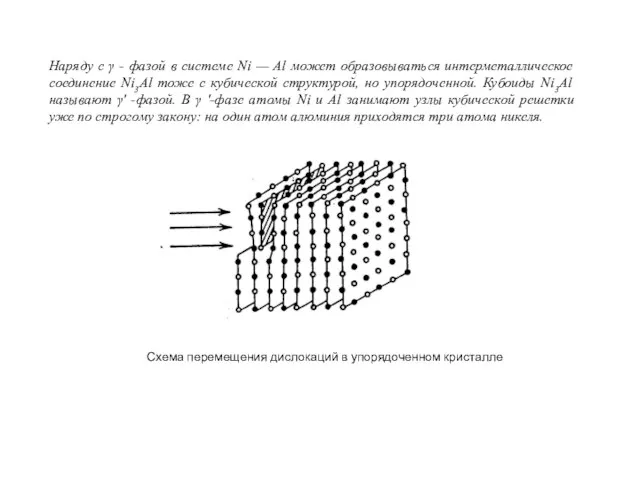
Наряду с γ - фазой в системе Ni — Аl может образовываться интерметаллическое соединение Ni3Аl тоже с кубической структурой, но упорядоченной. Кубоиды Ni3Аl называют γ' -фазой. В γ '-фазе атомы Ni и Аl занимают узлы кубической решетки уже по строгому закону: на один атом алюминия приходятся три атома никеля.
Схема перемещения дислокаций в упорядоченном кристалле

Cхема закрепления дислокации включениями другой фазы. ДД – движущаяся дислокация.
Чтобы получить суперсплав, расплавляют никель и смешивают с алюминием. При охлаждении расплавленной смеси сначала затвердевает неупорядоченная γ-фаза (ее температура кристаллизации высока), а затем внутри нее при понижении температуры формируются небольшие по размерам кубоиды γ'-фазы.
Варьируя скорость охлаждения, можно регулировать кинетику образования, а значит и размеры включений γ'-фазы Ni3Аl.

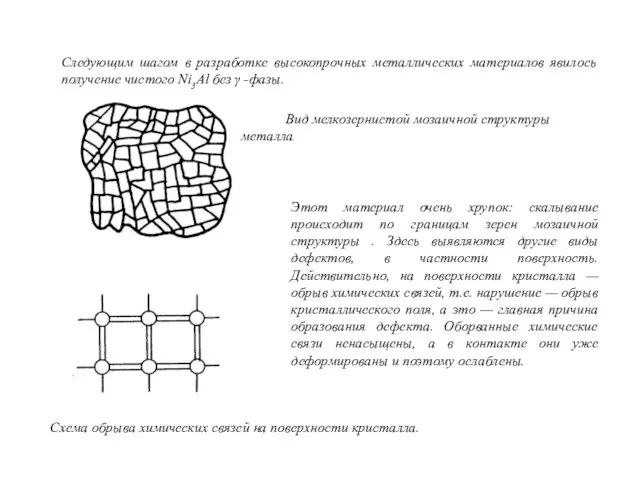
Следующим шагом в разработке высокопрочных металлических материалов явилось получение чистого Ni3Al без γ -фазы.
Вид мелкозернистой мозаичной структуры металла.
Этот материал очень хрупок: скалывание происходит по границам зерен мозаичной структуры . Здесь выявляются другие виды дефектов, в частности поверхность. Действительно, на поверхности кристалла — обрыв химических связей, т.е. нарушение — обрыв кристаллического поля, а это — главная причина образования дефекта. Оборванные химические связи ненасыщены, а в контакте они уже деформированы и поэтому ослаблены.
Схема обрыва химических связей на поверхности кристалла.

Для устранения этих дефектов надо:
либо изготавливать монокристаллический материал, не содержащий отдельных зерен-кристаллитов ;
либо найти «буфер» в виде примесей, которые не проникали бы в заметных количествах в объем Ni3Al, но хорошо адсорбировались бы на поверхности и заполняли вакансии. Наибольшим сродством к вакансиям обладают изовалентные примеси, т.е. примеси, атомы которых находятся в той же группе Периодической системы, что и атом, удаленный из кристаллической решетки и образовавший вакансию.
Суперсплавы Ni3Al<В> и Ni3Al
сегодня широко применяются как жаропрочные материалы при температурах до 1000°С. Аналогичные суперсплавы на основе кобальта имеют несколько меньшую прочность, но сохраняют ее вплоть до температуры 1100°С. Дальнейшие перспективы связаны с получением интерметаллических соединений TiAl и Тi3Аl в чистом виде. Детали, изготовленные из них, оказываются на 40 % легче, чем те же детали из никелевого суперсплава.

Сплавы с легкой деформируемостью под нагрузкой.
Методом создания таких металлических материалов является изготовление структуры с зернами-кристаллитами очень малых размеров.
Зерна, имеющие размеры менее 5 мкм, под нагрузкой скользят друг по другу без разрушения. Образец, состоящий из таких зерен, выдерживает без разрушения относительное растяжение Δl/l0 = 10 , т.е. длина образца увеличивается на 1000 % от первоначальной длины. Это — эффект сверхпластичности. Он объясняется деформацией связей в контактах зерен, т.е. большим количеством поверхностных дефектов.
Сверхпластичный металл можно обрабатывать почти как пластилин, придавая ему желаемую форму, а затем деталь из такого материала термообрабатывают для укрупнения зерен и быстро охлаждают, после чего эффект сверхпластичности исчезает, и деталь используют по назначению.
Главная трудность при получении сверхпластичных металлов состоит в достижении мелкодисперсной зернистой структуры.

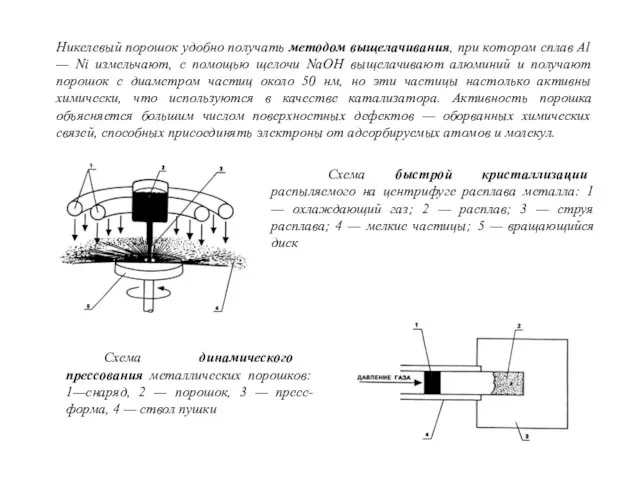
Никелевый порошок удобно получать методом выщелачивания, при котором сплав Al — Ni измельчают, с помощью щелочи NaOH выщелачивают алюминий и получают порошок с диаметром частиц около 50 нм, но эти частицы настолько активны химически, что используются в качестве катализатора. Активность порошка объясняется большим числом поверхностных дефектов — оборванных химических связей, способных присоединять электроны от адсорбируемых атомов и молекул.
Схема быстрой кристаллизации распыляемого на центрифуге расплава металла: 1 — охлаждающий газ; 2 — расплав; 3 — струя расплава; 4 — мелкие частицы; 5 — вращающийся диск
Схема динамического прессования металлических порошков: 1—снаряд, 2 — порошок, 3 — пресс-форма, 4 — ствол пушки

Метод лазерного глазурирования. Термин заимствован из фарфорового (керамического) производства. С помощью лазерного излучения расплавляется тонкий слой на поверхности металла и применяется быстрое охлаждение со скоростями порядка 107К/с.
Предельным случаем сверхбыстрого твердения является получение аморфных металлов и сплавов — металлических стекол.

Сверхпроводящие металлы и сплавы
В 1911 г. в Голландии Камерлинг-Оннес открыл уменьшение удельного сопротивления ртути при температуре кипения жидкого гелия (4,2 К) до нуля! Переход в сверхпроводящее состояние (ρ = 0) происходил скачком при некоторой критической температуре Тс. До 1957 г. явление сверхпроводимости не имело физического объяснения, хотя мир был занят поиском все новых и новых сверхпроводников. Так, к 1987 г. было известно около 500 металлов и сплавов с разными значениями Тс. Максимальной Тс обладали соединения ниобия.

Незатухающий ток. Если в металлическом кольце возбудить электрический ток, то при обычной, например, комнатной температуре он быстро затухает, поскольку протекание тока сопровождается тепловыми потерями. При Т ≈ 0 в сверхпроводнике ток становится незатухающим. В одном из опытов ток циркулировал в течение 2,5 лет, пока не прекратили.
Поскольку ток течет без сопротивления, а количество выделяемого током тепла
Q=0,24I2Rt,
то в случает R = 0 тепловые потери просто отсутствуют.
Излучение в сверхпроводящем кольце отсутствует по причине квантования. Но в атоме квантуются (принимают дискретные значения) импульс и энергия одного электрона, а в кольце — ток, т.е. вся совокупность электронов. Таким образом, мы имеем пример кооперативного явления — движение всех электронов в твердом теле строго согласовано!

Эффект Мейснера
Открыт в 1933 г. Его сущность состоит в том, что внешнее магнитное поле при Т < Тс не проникает в толщу сверхпроводника. Экспериментально это наблюдается при Т=Тс в виде выталкивания сверхпроводника из магнитного поля, как и полагается диамагнетику. Этот эффект объясняется тем, что в поверхностном слое толщиной 0,1 мкм внешнее магнитное поле индуцирует постоянный ток, но тепловых и излучательных потерь нет и в результате вокруг этого тока возникает постоянное незатухающее магнитное поле. Оно противоположно по направлению внешнему полю (принцип Ле-Шателье) и экранирует толщу сверхпроводника от внешнего магнитного поля.
При увеличении Н до некоторого значения Нс сверхпроводимость разрушается. Значения Нс лежат в интервале 10-2 ... 10-1 Т для различных сверхпроводников.
http://www.youtube.com/watch?v=bo5XTURGMTM

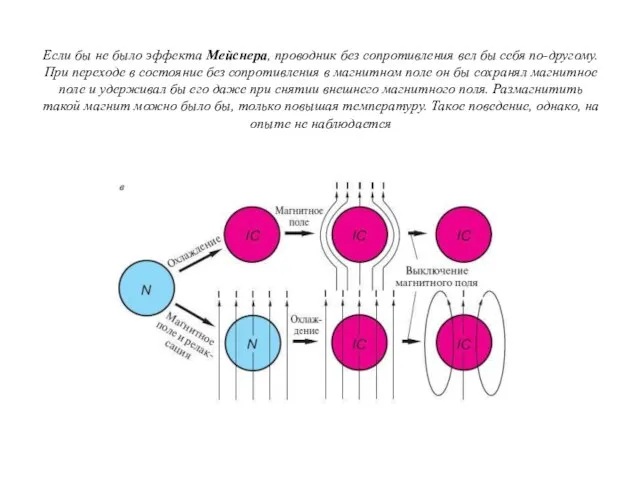
Если бы не было эффекта Мейснера, проводник без сопротивления вел бы себя по-другому. При переходе в состояние без сопротивления в магнитном поле он бы сохранял магнитное поле и удерживал бы его даже при снятии внешнего магнитного поля. Размагнитить такой магнит можно было бы, только повышая температуру. Такое поведение, однако, на опыте не наблюдается

Помимо рассмотренных сверхпроводников, которые получили название сверхпроводников первого рода, были открыты (А, В. Шубников, 1937.; А. А. Абрикосов, 1957 г.) сверхпроводники второго рода.
В них внешнее магнитное поле при достижении некоторого Нс1 проникает в образец, и электроны, скорости которых направлены перпендикулярно Н, под влиянием силы Лоренца начинают двигаться по окружности. Возникают вихревые нити. «Ствол» нити получается несверхпроводящим металлом, а вокруг него движутся электроны сверхпроводимости. В результате образуются смешанный сверхпроводник, состоящий из двух фаз — сверхпроводящей и нормальной. Только при достижении другого, более высокого значения Нc2 нити, расширяясь, сближаются, и сверхпроводящее состояние разрушается полностью. Значения Нс2 достигают 20...50 Т у таких сверхпроводников, как Nb3Sn и PbMo6O8 соответственно.

Схема джозефсоновской структуры:
1-диэлектрическая прослойка;
2-сверхпроводники
Структура состоит из двух сверхпроводников, разделенных диэлектрической тонкой прослойкой. Эта структура находится при некоторой разности потенциалов, задаваемой внешним напряжением V. Из теории, развитой Фейнманом, следует выражение для тока I, протекающего через структуру:
I= I0sin [(2eV/h)t+ φ0],
где I0 = 2Кρ/h (К - константа взаимодействия обоих сверхпроводников в джозефсонской структуре; ρ — плотность частиц, переносящих сверхпроводящий ток).
Величина φ0 = φ2 - φ1 рассматривается как разность фаз волновых функций электронов в контактирующих сверхпроводниках.
Видно, что даже в отсутствие внешнего напряжения (V = 0) через контакт течет постоянный ток. Это и есть стационарный эффект Джозефсона.
Если поместить джозефсоновскую структуру в магнитное поле, то магнитный поток Ф вызывает изменение Δφ, и в результате получаем:
I= I0sinφ0 cos (Ф / Ф0) ,
где Ф0 — квант магнитного потока.
Величина Ф0 = hс/е равна 2,07·10-11 Т·см2. Столь малое значение Ф0 позволяет изготавливать сверхчувствительные измерители магнитного поля (магнитомеры), фиксирующие слабые магнитные поля от биотоков мозга и сердца.

Уравнение
I= I0sin [(2eV/h)t+ φ0]
показывает, что в случае V ≠ 0 ток будет осциллировать с частотой f=2eV/h. Численно f попадает в микроволновый диапазон. Таким образом, джозефсоновский контакт позволяет создавать переменный ток с помощью постоянной разности потенциалов. Это — нестационарный эффект Джозефсона.
Переменный джозефсоновский ток так же, как и обычный ток в колебательном контуре, будет излучать электромагнитные волны, и это излучение действительно наблюдается на опыте. Для высококачественных джозефсоновских S — I — S контактов толщина диэлектрической прослойки I должна быть чрезвычайно малой — не более нескольких нанометров. В противном случае сильно снижается константа связи К, определяющая ток I0 . Но тонкая изолирующая прослойка деградирует с течением времени из-за диффузии атомов из сверхпроводящих материалов. Кроме того, тонкая прослойка и значительная диэлектрическая постоянная ее материала приводит к большой электрической емкости структуры, что ограничивает ее практическое использование.

Основные качественные представления о физике явления сверхпроводимости.
Механизм образования куперовских пар
Рассмотрим пару электронов е1 и e2, которые отталкиваются кулоновским взаимодействием. Но существует и другое взаимодействие: например, электрон е1 притягивает один из ионов I и смещает его из положения равновесия. Ион I создает электрическое поле, действующее на электроны. Поэтому его смещение повлияет и на другие электроны, например, на e2. Таким образом, возникает взаимодействие электронов е1 и e2 через кристаллическую решетку. Электрон притягивает ион, но так как Z1 > Z2, то электрон вместе с ионной «шубой» имеет положительный заряд и притягивает второй электрон.
При Т > Тс тепловое движение размывает ионную «шубу». Смещение иона — это возбуждение атомов решетки, т.е. не что иное, как рождение фонона. При обратном переходе излучается фонон, и он поглощается другим электроном. Значит взаимодействие электронов — это обмен фононами. В результате весь коллектив электронов твердого тела оказывается связанным.
В каждый данный момент электрон сильнее связан с одним из электронов в этом коллективе, т.е. весь электронный коллектив как бы состоит из электронных пар. Внутри пары электроны связаны определенной энергией. Поэтому повлиять на эту пару могут лишь те воздействия, которые преодолеют энергию связи. Оказывается, что обычные столкновения изменяют энергию на очень малую величину, и она не оказывает влияния на электронную пару. Поэтому электронные пары движутся в кристалле без столкновений, без рассеяния, т.е. сопротивление току равно нулю.