Содержание
- 2. Содержание: Для продолжения работы щелкните мышкой по соответствующей теме Понятие частного целого неотрицательного числа и натурального;
- 3. Деление целого неотрицательного числа на натуральное В начальной школе знакомство с делением происходит при рассмотрении 2-х
- 4. сколько классов (учеников) получилось. Деление целого неотрицательного числа на натуральное (продолжение) Деление по содержанию Составьте задачу
- 5. сколько элементов (тетрадей) в каждом классе. Деление целого неотрицательного числа на натуральное (продолжение) Деление на равные
- 6. Значение выражений 6 : 3 и 6 : 2 дети могут найти, используя результат, полученный в
- 7. Связь деления с умножением (продолжение) Определение 17 лежит в основе следующего общего правила для нахождения результата
- 8. Связь деления с умножением (продолжение) Ознакомление младших школьников с этими правилами может проводиться при рассмотрении троек
- 9. Связь деления с умножением (продолжение) Для продолжения работы вернитесь в оглавление. Запишите это в тетрадь и
- 10. Правило 2: Если выражение содержит одновременно действия сложение или вычитание, а так же умножение или деление,
- 11. Отношение делимости В начальной школе дети сталкиваются со случаями невыполнимости действия деления на множестве целых неотрицательных
- 12. Продолжите предложение. Чтобы проверить себя щелкните мышкой по кнопке с вопросом. Для продолжения работы щелкните мышкой
- 13. Задание: Перепишите данные выражения в три столбика по следующим признакам: 1-ый – те, которые имеют значение
- 14. на 9: Для того, чтобы целое неотрицательное число делилось на 9 необходимо и достаточно, чтобы Отношение
- 15. Задача, выгравированная на надгробном камне Диафанта – греческого математика, жившего в III веке н. э. Путник!
- 16. Отношение делимости. Признаки делимости. (продолжение) Задание: Решите данные задачи, используя в рассуждениях признаки делимости чисел. Древнеегипетская
- 17. Выберем из нее самое большое произведение, меньшее числа 23. Это произведение 2 ⋅ 3, 3 ⋅
- 18. В этой задаче множество A – тетрадей, n(A) = 13, разбивали на равночисленные подмножества (классы) по
- 19. II этап. Знакомство с первым требованием определения деления с остатком: 0 ≤ r На этом этапе
- 20. Деление с остатком. (продолжение) III этап. Знакомство с приемами подбора частного и нахождения остатка. На этом
- 21. Запишите данный пример и Ваши объяснения. Для продолжения работы щелкните мышкой по голубому полю экрана. Деление
- 22. Свойства деления Для действия деления справедливы следующие свойства (законы): Деление суммы на число; Деление разности на
- 23. Свойства деления (продолжение) Запишите это в тетрадь и щелкните мышкой по голубому полю экрана Сформулируйте это
- 24. Щелкните мышкой по оранжевому или зеленому кругу и Вы увидите иллюстрацию для объяснения одного из способов
- 25. Задание: Решите задачу разными способами. Способы решения задачи запишите выражением и к каждому способу напишите план
- 26. Свойства деления (продолжение) Деление произведения на число Данное свойство можно сформулировать в виде правила: Чтобы произведение
- 27. Для продолжения работы щелкните мышкой по управляющей кнопке. Для просмотра иллюстраций к задачам, щелкните мышкой по
- 28. Изучение деления в начальном курсе математики I этап. Ознакомление с делением. На этом этапе дети знакомятся:
- 29. Изучение действия деления в НКМ (продолжение) Запишите это в тетрадь и щелкните мышкой по голубому полю
- 30. IVэтап Изучение алгоритмов письменного деления. (продолжение) знакомятся с алгоритмом деления на двузначное и многозначное число, при
- 31. Запишите это в тетрадь. Для ознакомления с каждым способом, щелкните мышкой по кругу, нарисованному рядом с
- 32. Способом округления: Округлим делитель 63 до числа 60.; 472 разделим на 60 = 6 ⋅ 10:
- 33. Способом округления: Округлим делитель 63 до числа 60.; 472 разделим на 60 = 6 ⋅ 10:
- 35. Скачать презентацию
Слайд 2Содержание:
Для продолжения работы щелкните мышкой по соответствующей теме
Понятие частного целого неотрицательного
Содержание:
Для продолжения работы щелкните мышкой по соответствующей теме
Понятие частного целого неотрицательного
Связь деления с умножением;
Свойства деления;
Алгоритм письменного деления;
Порядок действий;
Отношение делимости. Теорема о единственности частного. Признаки делимости;
Деление с остатком.
Завершение работы
Множество No
Умножение
Сложение
Вычитание
С помощью этих кнопок можно перейти в электронные конспекты по указанным темам. Изучение действия деления в начальном курсе математики.
Для возвращения в данный конспект нажмите
Слайд 3Деление целого неотрицательного числа на натуральное
В начальной школе знакомство с делением происходит
Деление целого неотрицательного числа на натуральное
В начальной школе знакомство с делением происходит

Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Для продолжения работы вернитесь в оглавление.
деление по содержанию;
деление на равные части.
Задание: Составьте данные задачи по сюжетам, которые появятся на экране после щелчка мышкой по оранжевому или зеленому кругам.
Продолжите предложение. Чтобы проверить себя щелкните мышкой по кнопке с вопросом. Для продолжения работы щелкните мышкой по голубому полю экрана.
При ознакомлении с делением младшие школьники для нахождения частного выполняют предметные действия с множеством, которое разбивают на равночисленные непересекающиеся подмножества (классы). Эти действия соответствуют такому определению частного:
Определение 15: Частным целого неотрицательного числа a и натурального числа b называется целое неотрицательное число с, которое является:
количеством классов, полученных при разбиении множества А, численность которого равна а (n(A)=а) на равночисленные классы по b элементов в каждом;
численностью класса, полученного при разбиении множества А, численность которого равна а (n(A)=а) на b равночисленных классов.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Определение 16: Действие, посредством которого находится частное, называется деление.
Числа называются: a – делимое, b – делитель, с – частное,
запись a : b так же называется – частное.
Задание: Укажите, какая часть определения 15 относится к случаю
деления по содержанию, а какая к случаю деления на равные части.
Слайд 4сколько классов (учеников) получилось.
Деление целого неотрицательного числа на натуральное (продолжение)
Деление по содержанию
Составьте
сколько классов (учеников) получилось.
Деление целого неотрицательного числа на натуральное (продолжение)
Деление по содержанию
Составьте

Для продолжения работы щелкните мышкой по голубому полю экрана.
В этой задаче множество A – тетрадей, n(A) = 12, разбили на равночисленные подмножества (классы) по 3 элемента (тетради) в каждом. Решая задачу, дети выясняют,
Запишите это в тетрадь. продолжив предложение.
Чтобы проверить себя щелкните мышкой по кнопке с вопросом.
Задание: Составьте свою задачу на данный вид деления и разберите ее с точки зрения теории множеств.
Выполните задание.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Слайд 5 сколько элементов (тетрадей) в каждом классе.
Деление целого неотрицательного числа на натуральное
сколько элементов (тетрадей) в каждом классе.
Деление целого неотрицательного числа на натуральное

Деление на равные части
Составьте задачу по данной иллюстрации.
Для продолжения работы щелкните мышкой по голубому полю экрана.
В этой задаче множество A – тетрадей, n(A) = 12, разбили на 3 равночисленных класса (раздали трем ученикам). Решая задачу, дети выясняют,
Задание: Составьте свою задачу на данный вид деления и разберите ее с точки зрения теории множеств.
Выполните задание.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Запишите это в тетрадь. продолжив предложение.
Чтобы проверить себя щелкните мышкой по кнопке с вопросом.
Слайд 6Значение выражений 6 : 3 и 6 : 2 дети могут найти,
Значение выражений 6 : 3 и 6 : 2 дети могут найти,

Связь деления с умножением
Определение 17: Частным целого неотрицательного числа a и натурального числа b называется целое неотрицательное число с, являющееся корнем уравнения: х ⋅ b = а или b ⋅ х = а.
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Запишите это в тетрадь и выполните задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Задание: Запишите рассуждения детей при решении примера 6 : 2.
Для продолжения работы щелкните по управляющей кнопке.
При ознакомлении с делением младшие школьники находят результат, производя предметные действия с множествами.
Знания взаимосвязи между действиями умножение и деление позволяет перейти от предметных поисков результата действия деления, к поиску ответа с помощью рассуждений.
3 ⋅ 2 = 6
6 : 3 = 2
6 : 2 = 3
Задание: Сформулируйте задания для получения 2-го и 3-го равенства.
В основе таких рассуждений лежит следующее определение частного:
Для установления этой взаимосвязи, можно предложить детям задание:
Нарисуй треугольники в 2 столбика по 3 в каждом. Сколько треугольников получилось?
Отвечая на данный вопрос, дети составят равенство.
Учитель может предложить детям два обратных задания, после выполнения которых дети получат еще два равенства.
Таким образом: верно утверждение: «а : b = с тогда и только тогда, когда b ⋅ с = а».
Слайд 7Связь деления с умножением (продолжение)
Определение 17 лежит в основе следующего общего правила
Связь деления с умножением (продолжение)
Определение 17 лежит в основе следующего общего правила

«Чтобы найти частное можно подобрать такое число, которое при умножении на делитель дает делимое»
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Определение 17 связывает действия __________ и ________. Используя это определение, можно вывести правила нахождения неизвестного числа в этих действиях по известному результату и второму числу.
нахождение неизвестного множителя
нахождение неизвестного делимого
нахождение неизвестного делителя
Это правила:
умножение
деление
Чтобы найти неизвестный множитель, достаточно произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, достаточно частное умножить на делитель.
Чтобы найти неизвестный делитель, достаточно делимое разделить на частное.
Сформулируйте и запишите эти правила. Чтобы проверить себя, щелкните мышкой кругу рядом с названием соответствующего правила.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Запишите это в тетрадь, вставив пропущенные названия действий.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Слайд 8Связь деления с умножением (продолжение)
Ознакомление младших школьников с этими правилами может проводиться
Связь деления с умножением (продолжение)
Ознакомление младших школьников с этими правилами может проводиться

8 : 2 = 4
4 ⋅ 2 = 8
8 : 4 = 2
Эти тройки могут быть даны детям в готовом виде или могут быть получены ими в результате решения взаимно обратных задач. Пример такой работы был рассмотрен в конспекте «ВычитаниЭти тройки могут быть даны детям в готовом виде или могут быть получены ими в результате решения взаимно обратных задач. Пример такой работы был рассмотрен в конспекте «Вычитание».
Для продолжения работы щелкните мышкой по управляющей кнопке.
Задание: Придумайте задачи и обратные им для введения правил нахождения неизвестных делимого и делителя и нахождения неизвестного множителя. Продумайте иллюстрацию этих задач. Запишите вопросы учителя и предполагаемые ответы учеников.
Если Вы хотите перейти в конспект «Вычитание» и еще раз посмотреть пример работы с задачами, щелкните мышкой по выделенному слову «вычитание». Для возвращения можно нажать клавишу 6 ⋅ 4 = 24 проверяем: шесть умножить на четыре – получится двадцать четыре. Решение уравнений. После ознакомления с правилами нахождения неизвестного числа в действиях умножение и деление дети могут решать простейшие уравнения вида: 6 ⋅ х = 24 х : 4 = 7 36 : х = 9 Задание: Запишите рассуждения учеников при решении оставшихся уравнений. Рассуждения учеников при решении уравнения могут быть такими: 6 ⋅ х = 24 уравнение содержит действие умножение, значит нам неизвестен 2-ой множитель; х = 24 : 6 х = 4 Запишите это в тетрадь и щелкните мышкой по голубому полю экрана Выполните предложенное задание. чтобы найти 2-ой множитель, мы произведение 24 разделим на 1-ый множитель 6 и находим х. 2-ой множитель равен 4.
Выполните предложенное задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Слайд 9Связь деления с умножением (продолжение)
Для продолжения работы вернитесь в оглавление.
Запишите это
Связь деления с умножением (продолжение)
Для продолжения работы вернитесь в оглавление.
Запишите это

Младшие школьники знакомятся также с уравнениями, состоящими из двух и более действий. Например:
Задание: Запишите рассуждения учеников при решении этих уравнений. Чтобы посмотреть пример рассуждения, щелкните мышкой по кнопке со знаком вопроса, при повторном щелчке подсказка исчезнет.
(х + 25) : 7 = 8
(х ⋅ 16) – 6 = 90
160 : (х + 26) = 4
28 – (45 : х) = 13
Выполните это задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
(х ⋅ 16) – 6 = 90
х ⋅ 16 = 90 + 6
х ⋅ 16 = 96
х = 96 : 16
х = 6
Неизвестное содержится в выражении (х ⋅ 16), значит нам неизвестно уменьшаемое;
Чтобы найти это уменьшаемое, мы к разности 90 прибавим вычитаемое 6. Получаем 96.
Полученное уравнение содержит действие умножение, значит нам неизвестен 1-ый множитель.
Чтобы найти 1-ый множитель, мы произведение 96 разделим на 2-ой множитель 16. Получаем 6.
(6 ⋅ 16) – 6 = 90
96
Проверяем: 6 ⋅ 16 = 96; 96 – 6 = 90.
В данном уравнении последнее действие – вычитание;
С помощью определения 17 можно объяснить невозможность деления на 0.
Действительно:
если а ≠ 0, то нет такого целого неотрицательного числа, которое бы при умножении на ноль равнялось бы а ≠ 0, так как при умножении любого числа на ноль получается ноль.
а : 0 невозможно!!!
если а = 0, то значение выражения 0 : 0 неопределенно, так как любое число можно умножить на ноль, чтобы получить ноль.
Невозможность деления на 0
Слайд 10Правило 2: Если выражение содержит одновременно действия сложение или вычитание, а так
Правило 2: Если выражение содержит одновременно действия сложение или вычитание, а так

сначала выполняются действия умножение и деление по порядку, а затем сложение и вычитание по порядку.
Деление целого неотрицательного числа на натуральное (продолжение)
Задание 1: Запишите выражение:
Сумму трехсот шестидесяти девяти и четырехсот семидесяти одного разделить на разность чисел: восемьсот семьдесят два и восемьсот тридцать девять.
Знакомство с порядком выполнения действий начинается в 1-ом классе, когда дети приступают к решению примеров в два и более действий. После введения всех арифметических действий: сложение, вычитание, умножение и деление, дети обобщают полученные знания и формулируют следующие правила:
Порядок действий
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Правило 1: Если выражение содержит только действия сложение и вычитание или только действия умножение и деление, то
действия в выражении могут выполняться по порядку.
Правило 3: Если выражение содержит скобки, то
сначала выполняются действия в скобках с учетом правил 1 и 2, а потом все остальные действия с учетом этих же правил.
Продолжите данные правила. Чтобы проверить себя щелкните мышкой по кнопкам с вопросом. Для продолжения работы щелкните мышкой по голубому полю экрана.
Выполните эти задания.
Чтобы посмотреть варианты чтения второго выражения щелкните по нему мышкой. При повторном щелчке подсказка исчезнет.
Для продолжения работы вернитесь в оглавление.
Задание 2: Запишите, как читается данное выражение:
Задание 3: Выполните действия в данных выражениях и запишите, что с точки зрения определения каждого арифметического действия Вы нашли.
38 ⋅ 48 : (39 + 37)
произведение тридцати восьми и сорока восьми разделить на сумму тридцати девяти и тридцати семи.
частное произведения тридцати восьми и сорока восьми и суммы тридцати девяти и тридцати семи.
Слайд 11Отношение делимости
В начальной школе дети сталкиваются со случаями невыполнимости действия деления на
Отношение делимости
В начальной школе дети сталкиваются со случаями невыполнимости действия деления на
Запишите это в тетрадь и выполните предлагаемое детям задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
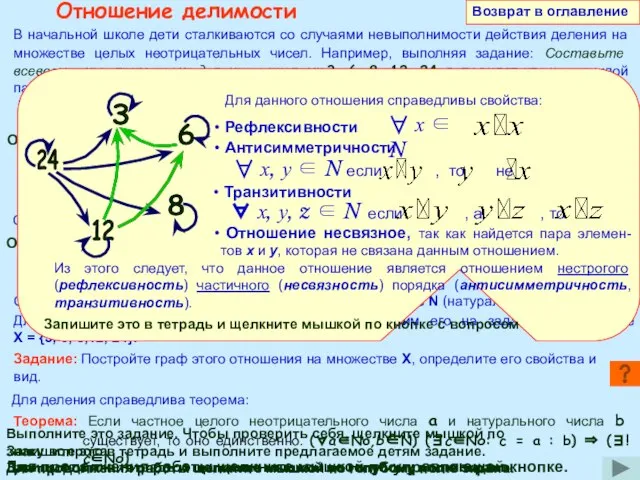
Выполняя это задание, мы на множестве {3, 6, 8, 12, 24} установили отношение делимости: Т(х, у) «х кратно у», которое можно определить так:
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Отношение Т(х, у) «х кратно у» рассматривают на множестве N (натуральных чисел).
Для определения свойств этого отношения, рассмотрим его на заданном множестве Х = {3, 6, 8,12, 24}.
Задание: Постройте граф этого отношения на множестве Х, определите его свойства и вид.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Теорема: Если частное целого неотрицательного числа a и натурального числа b существует, то оно единственно. (∀а∈No,b∈N) (∃с∈Nо: с = а : b) ⇒ (∃!с∈Nо)
Для деления справедлива теорема:
Выполните это задание. Чтобы проверить себя, щелкните мышкой по знаку вопроса.
Для продолжения работы щелкните мышкой по голубому полю экрана.
В этом случае говорят, что b делитель а.
3
6
8
24
12
Рефлексивности
Для данного отношения справедливы свойства:
Антисимметричности
Транзитивности
Из этого следует, что данное отношение является отношением нестрогого (рефлексивность) частичного (несвязность) порядка (антисимметричность, транзитивность).
Отношение несвязное, так как найдется пара элемен- тов х и у, которая не связана данным отношением.
Запишите это в тетрадь и щелкните мышкой по кнопке с вопросом
Слайд 12Продолжите предложение. Чтобы проверить себя щелкните мышкой по кнопке с вопросом. Для
Продолжите предложение. Чтобы проверить себя щелкните мышкой по кнопке с вопросом. Для
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Выполните задание. Чтобы посмотреть решение, щелкните кнопке с вопросом. При повторном щелчке подсказка исчезнет. Для продолжения работы уберите подсказку и щелкните мышкой по голубому полю экрана
Найдите НОД и НОК оставшихся чисел.
Для продолжения работы щелкните мышкой по управляющей кнопке.
1, 2, 3, 4, 6, 12.
Число 12 – НОД: D(a, b) = 12.
Например, числа 60 и 24 имеют общие делители:
Определение 20: Общим делителем натуральных чисел a и b называется всякое натуральное число с, являющееся делителем каждого из данных чисел.
Отношение делимости. (продолжение)
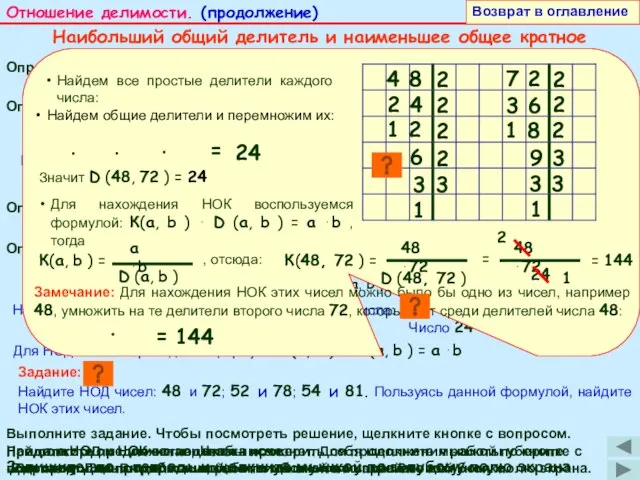
Наибольший общий делитель и наименьшее общее кратное
Определение 21: Наибольшим общим делителем (НОД) натуральных чисел a и b называется наибольшее число из всех общих делителей данных чисел.
НОД чисел a и b обозначают: D (a, b ).
Определение 23: Наименьшим общим кратным (НОК) натуральных чисел a и b называется наименьшее число из всех общих кратных данных чисел.
НОК чисел a и b обозначают: К(a, b ).
Определение 22: Общим кратным натуральных чисел a и b называется всякое натураль-ное число с, которое кратно каждому из данных чисел.
24, 48, 72,…
Число 24 – НОК: К(a, b) = 24.
Например, числа 12 и 8 имеют общие кратные им числа:
Задание:
Найдите НОД чисел: 48 и 72; 52 и 78; 54 и 81. Пользуясь данной формулой, найдите НОК этих чисел.
Для НОД и НОК справедлива формула: К(a, b ) ⋅ D (a, b ) = a ⋅b
Найдем все простые делители каждого числа:
2
2
2
6
2
3
7 2
2
3 6
2
1 8
2
9
3
3
3
1
Найдем общие делители и перемножим их:
⋅
⋅
⋅
=
24
1 2
4 8
2 4
3
1
Значит D (48, 72 ) = 24
Для нахождения НОК воспользуемся формулой: К(a, b ) ⋅ D (a, b ) = a ⋅b , тогда
1
2
= 144
, отсюда:
Замечание: Для нахождения НОК этих чисел можно было бы одно из чисел, например 48, умножить на те делители второго числа 72, которых нет среди делителей числа 48:
⋅
144
=
Слайд 13Задание: Перепишите данные выражения в три столбика по следующим признакам:
1-ый –
Задание: Перепишите данные выражения в три столбика по следующим признакам:
1-ый –

2-ой – те, которые не имеют значение на множестве No, и это можно определить по признаку делимости;
3- ий – те, для которых признак применить нельзя?
чтобы уменьшаемое и вычитаемое делилось на это число.
Для того чтобы произведение делилось на число достаточно,
Для того чтобы разность делилась на число достаточно,
Отношение делимости (продолжение)
Признаки делимости
позволяют, не производя вычислений, определить: имеет ли рассматриваемое выражение, содержащее действие деление, значение на множестве No.
делимость суммы:
делимость разности:
делимость произведения:
чтобы каждое слагаемое суммы делилось на это число.
чтобы один из множителей делился на это число.
Допишите данные признаки делимости, пользуясь их математической записью.
Чтобы проверить себя, щелкните мышкой кругу рядом с названием признака.
Для продолжения работы щелкните мышкой по голубому полю экрана.
В школьном курсе рассматриваются следующие признаки делимости:
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Для того чтобы сумма делилась на число достаточно,
Задание: Объясните почему данные условия в признаках являются только достаточными? Подтвердите это данными примерами.
Выполните это задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
(60 - 20) : 5
(63 - 23) : 5
(64 + 28) : 4
(62 + 26) : 4
(60 ⋅ 28) : 14
(7 ⋅ 22) : 14
(60 - 23) : 5
(48 + 23) : 4
(13 ⋅ 17) : 5
(26 - 20) : 4
Для продолжения работы щелкните мышкой по управляющей кнопке.
Слайд 14на 9: Для того, чтобы целое неотрицательное число делилось на 9 необходимо
на 9: Для того, чтобы целое неотрицательное число делилось на 9 необходимо

Отношение делимости. Признаки делимости. (продолжение)
Признаки делимости на однозначные числа
позволяют, не производя вычислений, определить: делится ли заданное число на однозначное или нет. Рассмотрим эти признаки:
на 2: Для того, чтобы целое неотрицательное число делилось на 2 необходимо и достаточно, чтобы
последняя цифра числа была четной.
на 3: Для того, чтобы целое неотрицательное число делилось на 3 необходимо и достаточно, чтобы
сумма цифр числа была бы кратна 3 .
на 4: Для того, чтобы целое неотрицательное число делилось на 4 необходимо и достаточно, чтобы
две последние цифры числа составляли число, кратное 4.
на 5: Для того, чтобы целое неотрицательное число делилось на 5 необходимо и достаточно, чтобы
последняя цифра числа была бы 5 или 0
на 6: Для того, чтобы целое неотрицательное число делилось на 6 необходимо и достаточно, чтобы
это число было кратно 2 и 3.
на 7: Для того, чтобы целое неотрицательное число делилось на 7 необходимо и достаточно, чтобы
в значащей части числа разность полного числа десятков и удвоенной цифры единиц была бы кратна 7. Разность может быть отрицательной.
на 8: Для того, чтобы целое неотрицательное число делилось на 8 необходимо и достаточно, чтобы
три последние цифры числа составляли число кратное 8.
сумма цифр числа была бы кратна 9.
Допишите данные признаки делимости. Чтобы проверить себя, щелкните мышкой кругу рядом с названием признака. Для продолжения работы щелкните мышкой по голубому полю экрана.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Слайд 15Задача, выгравированная на надгробном камне Диафанта – греческого математика, жившего в III
Задача, выгравированная на надгробном камне Диафанта – греческого математика, жившего в III

Путник! Здесь прах погребен Диофанта,
И числа могут поведать, о чудо,
Сколь долог был век его жизни.
Часть шестую его представляло счастливое детство,
Двенадцатая часть протекла его жизни –
Пухом покрылся тогда подбородок.
Седьмую в бездетном браке провел Диофант.
Прошло пятилетье.
Он был осчастливлен рожденьем прекрасного первенца сына,
Коему рок половину лишь жизни счастливой и светлой,
Дал на земле по сравненью с отцом.
И в печали глубокой старец земного удела конец воспринял,
Переживши года четыре с тех пор, как сына лишился
Скажи, скольких лет жизни достигнув,
Смерть воспринял Диофант?
Отношение делимости. Признаки делимости. (продолжение)
Задание: Используя признаки делимости, для каждого из приведенных чисел определите однозначные числа, на которые оно делится.
438562, 76545, 384364, 161000
Признаки делимости можно использовать в рассуждениях при решении задач. Рассмотрим это на примере такой задачи:
Выполните это задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Решение:
1. Из условия задачи следует, что возраст Диофанта кратен числам 6, 12, и 7.
2. Этому условию удовлетво-ряют числа: 84, 168, 252 и т. д.
3. Проверим наиболее вероят-ное число 84 – НОК этих чисел:
Детство – 84 : 6 = 14 (лет);
Пухом покрылся подбородок – 84 : 12 = 7, 14 + 7 = 21 (год);
Бездетный брак – 84 : 7 = 12,
12 + 21 = 33 (года);
Рождение сына –
33 + 5 = 38 (лет);
Смерть сына – 84 : 2 = 42,
38 + 42 = 80 (лет);
Смерть Диофанта –
80 + 4 = 84 (года).
Ответ: 84 года.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Перепишите условие задачи. Попробуйте решить ее.
Чтобы проверить себя, щелкните мышкой по кнопке с вопросом.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Слайд 16Отношение делимости. Признаки делимости. (продолжение)
Задание: Решите данные задачи, используя в рассуждениях признаки
Отношение делимости. Признаки делимости. (продолжение)
Задание: Решите данные задачи, используя в рассуждениях признаки

Древнеегипетская задача:
Количество (число) и его четвертая часть дают вместе 15. Найти количество.
Древнеиндийская задача:
Есть кадамба цветок.
На один лепесток пчелок пятая часть опустилась.
Рядом тут же росла вся в цвету сименгда,
И на ней третья часть поместилась.
Разность их ты найди, трижды их ты сложи,
На кутай этих пчел посади.
Лишь одна не нашла себе места нигде,
Все летала то взад, то вперед
И везде ароматом цветов наслаждалась.
Назови теперь мне, подсчитавши в уме,
Сколько пчелок всего здесь собралось.
Число десятков двузначного числа составляет две трети числа единиц, а число, записанное теми же числами в обратном порядке, больше первоначального на 18. Найти число.
Придумайте десятизначное число, состоящее из неповторяющихся цифр, такое что первая слева цифра кратна 1, две первые слева цифры составляют число кратное 2, три первые слева цифры составляют число кратное 3 и т . д.
Решите эти задачи дома.
Для продолжения работы вернитесь в оглавление.
Слайд 17 Выберем из нее самое большое произведение, меньшее числа 23. Это произведение
Выберем из нее самое большое произведение, меньшее числа 23. Это произведение

2 ⋅ 3, 3 ⋅ 3, 4 ⋅ 3, 5 ⋅ 3, 6 ⋅ 3, 7 ⋅ 3, 8 ⋅ 3, …, 22 ⋅ 3, 23 ⋅ 3.
Деление с остатком
Определение 24: Целое неотрицательное число q называется частным, а целое неотрица-тельное число r – остатком от деления целого неотрицательного числа а на натуральное число b, если выполняются следующие условия: Запишите это в тетрадь и щелкните мышкой по голубому полю экрана Для продолжения работы, щелкните мышкой по голубому полю экрана Для продолжения работы, щелкните мышкой по управляющей кнопке. Теорема: Для любого целого неотрицательного числа a и любого натурального числа b существует и притом только одна пара целых неотрицательных чисел q и r , которые соответственно являются частным и остатком от деления a на b. Для деления справедлива теорема: Рассмотрим справедливость данной теоремы в различных случаях: a < b. a : b = 0 (ост. a). Например: а =3, b = 5, тогда : 3 : 5 = 0 (ост. 3) a = b. a : а = 1 (ост. 0). Например: а =3, b = 3, тогда: 3 : 3 = 1 (ост. 0) а > b. Например: а = 23, b = 3. Рассмотрим последовательность произведений: 7 ⋅ 3 Число 7 – искомое частное. Теперь найдем остаток. Деление без остатка можно рассматривать как частный случай деления с остатком. В этом случае остаток равен 0. Например: 24 : 3 = 8 (ост. 0). Запишите это в тетрадь. Составьте свой пример.
1. 0 ≤ r
(∀а ∈No,b∈N) (∃! q, r ∈Nо: а : b = q (ост. r))
Для этого от делимого отнимем выбранное произведение: 23 - 7 ⋅ 3 = 2.
Число 2 – искомый остаток. Запишем решение: 23 : 3 = 7 (ост. 2)
Для продолжения работы щелкните мышкой по голубому полю экрана
Слайд 18В этой задаче множество A – тетрадей, n(A) = 13, разбивали на
В этой задаче множество A – тетрадей, n(A) = 13, разбивали на

Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Можно выделить три этапа обучения младших школьников делению с остатком:
I этап. Знакомство с данным случаем деления и записью решения. На этом этапе дети выполняют предметные действия с множествами, в которых, при разбиении на равночисленные классы, остаются элементы, не образующие полный класс.
Задание: Составьте задачу по сюжету, который появится на экране.
Для продолжения работы, щелкните мышкой по голубому полю экрана
сколько полных классов (учеников) получилось и сколько элементов осталось в неполном классе.
Дети учатся записывать решение так: 13 : 4 = 3 (ост. 1).
Частное 3 показывает, , а остаток 1 показывает,
Продолжите предложение.
Чтобы проверить себя щелкните мышкой по кнопке с вопросом.
Для продолжения работы, щелкните мышкой по управляющей кнопке.
Деление с остатком. (продолжение)
Задание: Составьте свою задачу на деление с остатком. Запишите ее решение. Опишите это решение с точки зрения теории множеств.
Обучение младших школьников делению с остатком
Слайд 19II этап. Знакомство с первым требованием определения деления с остатком: 0 ≤
II этап. Знакомство с первым требованием определения деления с остатком: 0 ≤
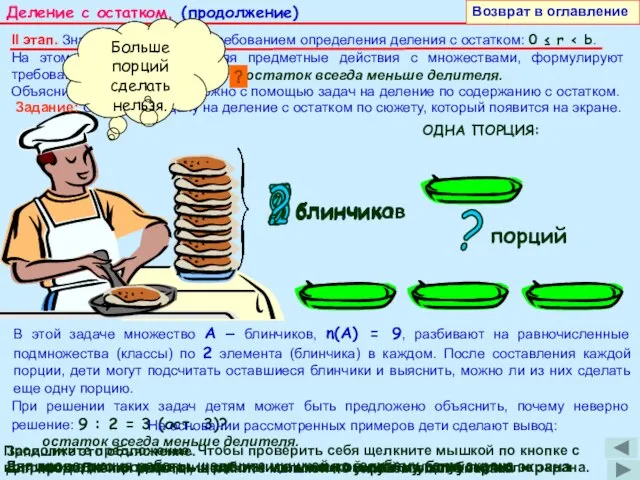
На этом этапе дети, выполняя предметные действия с множествами, формулируют требования к величине остатка:
блинчика
блинчик
5
3
1
7
9
?
Объяснить это требование можно с помощью задач на деление по содержанию с остатком.
остаток всегда меньше делителя.
Деление с остатком. (продолжение)
Продолжите предложение. Чтобы проверить себя щелкните мышкой по кнопке с вопросом. Для продолжения работы щелкните мышкой по голубому полю экрана.
Задание: Составьте задачу на деление с остатком по сюжету, который появится на экране.
Для продолжения работы, щелкните мышкой по голубому полю экрана
блинчиков
ОДНА ПОРЦИЯ:
?
порций
В этой задаче множество A – блинчиков, n(A) = 9, разбивают на равночисленные подмножества (классы) по 2 элемента (блинчика) в каждом. После составления каждой порции, дети могут подсчитать оставшиеся блинчики и выяснить, можно ли из них сделать еще одну порцию.
Можно сделать еще порцию?
Больше порций сделать нельзя.
При решении таких задач детям может быть предложено объяснить, почему неверно решение: 9 : 2 = 3 (ост. 3)?
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
На основании рассмотренных примеров дети сделают вывод:
Запишите это объяснение.
Для продолжения работы, щелкните мышкой по голубому полю экрана
Для продолжения работы, щелкните мышкой по управляющей кнопке.
остаток всегда меньше делителя.
Слайд 20Деление с остатком. (продолжение)
III этап. Знакомство с приемами подбора частного и нахождения
Деление с остатком. (продолжение)
III этап. Знакомство с приемами подбора частного и нахождения

На этом этапе дети учатся подбирать частное и находить остаток без выполнения предметных действий. Например, чтобы 17 разделить на 5 с остатком, они учатся рассуждать так: Найдем самое большое число до семнадцати, которое делится на пять. Это число – пятнадцать. 15 : 5 = 3 – это частное.
Найдем остаток: 17 - 15 = 2. Значит 17 : 5 = 3 (ост. 2).
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Для проверки полученных частного и остатка дети учатся таким рассуждениям:
Чтобы проверить правильность ответа мы
проверим сначала остаток: 2 < 5 (остаток меньше делителя);
проверим частное: три умножим на делитель пять и к полученному результату прибавим остаток два: 3 ⋅ 5 = 15; 15 + 2 = 17. Получили делимое 17, значит частное и остаток найдены верно.
Таким образом, на частных примерах дети проверяют оба требования, предъявляемые к частному q и остатку r:
Умение проверять полученный результат позволяет применять метод подбора в тех случаях, когда трудно подобрать самое большое число, меньшее делимого, которое делится на делитель. Например, при нахождении частного и остатка в случае 87 : 27 дети могут рассуждать так: Попробуем в частном число 2: 27 ⋅ 2 = 54, тогда остаток будет равен 87 – 54 = 33, 33 > 27 (остаток больше делителя), значит 2 – мало.
Попробуем в частном число 3: 27 ⋅ 3 = 81,тогда остаток будет равен 87 – 81 = 6, 6 < 27 (остаток меньше делителя), значит 6 – остаток, а 3 – частное:
87 : 27 = 3 (ост. 6).
1. 0 ≤ r Продолжите предложение. Чтобы проверить себя щелкните мышкой по кнопке с вопросом. Для продолжения работы щелкните мышкой по голубому полю экрана. Для продолжения работы, щелкните мышкой по управляющей кнопке.
Слайд 21Запишите данный пример и Ваши объяснения.
Для продолжения работы щелкните мышкой по
Запишите данный пример и Ваши объяснения.
Для продолжения работы щелкните мышкой по
Деление с остатком. (продолжение)
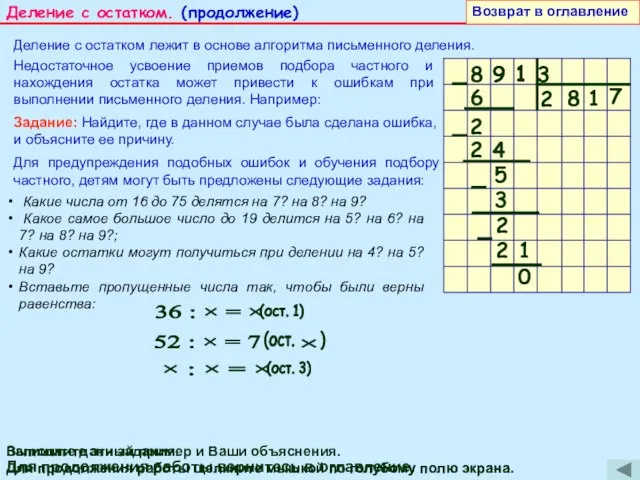
Деление с остатком лежит в основе алгоритма письменного деления.
8 9 1 3
2
6
2
9
8
2 4
2
0
2 1
1
7
Недостаточное усвоение приемов подбора частного и нахождения остатка может привести к ошибкам при выполнении письменного деления. Например:
5
3
1
Задание: Найдите, где в данном случае была сделана ошибка, и объясните ее причину.
Для предупреждения подобных ошибок и обучения подбору частного, детям могут быть предложены следующие задания:
Какие числа от 16 до 75 делятся на 7? на 8? на 9?
Какое самое большое число до 19 делится на 5? на 6? на 7? на 8? на 9?;
Какие остатки могут получиться при делении на 4? на 5? на 9?
Вставьте пропущенные числа так, чтобы были верны равенства:
Выполните эти задания.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Для продолжения работы вернитесь в оглавление.
Слайд 22Свойства деления
Для действия деления справедливы следующие свойства (законы):
Деление суммы на число;
Свойства деления
Для действия деления справедливы следующие свойства (законы):
Деление суммы на число;

Деление произведения на число;
Деление числа на произведение.
Запишите это в тетрадь.
Для продолжения работы щелкните мышкой по выбранному свойству.
После ознакомления со свойствами щелкните мышкой по голубому полю экрана.
Задание: Для данных выражений :
39 : 3
68 : 4
680 : 4
560 : 8
5600 : 80
Для продолжения работы вернитесь в оглавление.
запишите развернутое решение и найдите значение;
опишите, что с точки зрения каждого определения действия деления Вы нашли;
определите какое свойство лежит в основе вычислительного приема;
придумайте задачу, иллюстрирующую данное свойство запишите все способы решения данной задачи, составлением числовых выражений;
к каждому способу запишите план решения задачи.
Слайд 23Свойства деления (продолжение)
Запишите это в тетрадь и щелкните мышкой по голубому полю
Свойства деления (продолжение)
Запишите это в тетрадь и щелкните мышкой по голубому полю

Сформулируйте это правило. Чтобы проверить себя щелкните мышкой по знаку вопроса. Для продолжения работы щелкните мышкой по голубому полю экрана.
Выполните это задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Задание: Составьте задачу для ознакомления детей с правилом Деление суммы на число по иллюстрации, которая появится после щелчка мышкой по оранжевому кругу.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Деление суммы на число
В начальной школе знакомство с данным свойством сводится к знакомству с правилом:
Чтобы сумму разделить на число можно на это число разделить каждое слагаемое и полученные результаты (частные) сложить.
Для знакомства с данным правилом можно предложить детям задачу, имеющую два способа решения. Числа в условии подбирают так, чтобы все вычисления проходили в пределах таблицы умножения и соответствующих случаев деления.
Правило «Деление суммы на число» лежит в основе вычислительных приемов деления двузначного числа на однозначное. Например:
Запишите развернутое решение каждого примера;
Запишите рассуждения ученика при решении этих примеров;
Чем отличаются приемы решения примеров 1-ого и 2-ого столбика.
87 : 3
36 : 3
48 : 4
60 : 5
Для просмотра примера записи и рассуждений ученика, щелкните мышкой по знаку вопроса. При повторном щелчке подсказка исчезнет.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Решите составленную задачу различными способами, записав решение выражением.
Запишите план решения задачи в каждом способе.
Составьте план анализа решения, который приведет к выводу правила.
87 : 3
Рассуждения ученика:
представляю число 87 в виде суммы удобных слагаемых: 1-ое слагаемое – самое большое круглое число до восьмидесяти, которое делится на 3 – это 60 , тогда 2-ое слагаемое – это число 27;
= (60 + 27) : 3
= 60 : 3 + 27 : 3
= 20 + 9 = 29
нам удобно сначала каждое слагаемое разделить на 3;
затем сложить полученные результаты (частные) 20 и 9, и получаем 29.
Следует обратить внимание детей, что подобная задача не всегда имеет два способа решения. Задание: Измените условие данной задачи так, чтобы ее нельзя было решить вторым способом.
Задание:
Слайд 24Щелкните мышкой по оранжевому или зеленому кругу и Вы увидите иллюстрацию для
Щелкните мышкой по оранжевому или зеленому кругу и Вы увидите иллюстрацию для
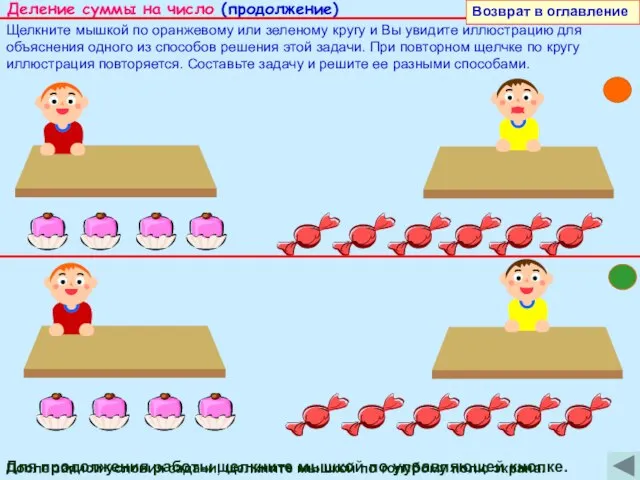
Деление суммы на число (продолжение)
Для продолжения работы щелкните мышкой по управляющей кнопке.
После записи условия задачи, щелкните мышкой по голубому полю экрана.
Слайд 25Задание: Решите задачу разными способами.
Способы решения задачи запишите выражением и к
Задание: Решите задачу разными способами.
Способы решения задачи запишите выражением и к

Свойства деления (продолжение)
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Для продолжения работы щелкните мышкой по управляющей кнопке.
Деление разности на число
Данное свойство можно сформулировать в виде правила:
Чтобы разность разделить на число можно на это число сначала разделить уменьшаемое, затем вычитаемое и из первого результата (частного) вычесть второй.
В начальной школе дети специально не знакомятся с данным правилом, но при выполнении некоторых заданий сталкиваются с его применением. Например:
1. Сравни выражения:
(18 – 6) : 3 … 18 : 3 – 6
(18 – 6) : 3 … 18 : 3 – 6 : 3
(18 – 6) : 3 … 18 – 6 : 3
2. Реши задачу разными способами:
В шести вазах стояло по равному количеству цветов, всего 30 штук. Взяли 12 цветов так, что в вазах осталось цветов поровну. Сколько цветов осталось в каждой вазе?
Сформулируйте это правило. Чтобы проверить себя щелкните мышкой по знаку вопроса. Для продолжения работы щелкните мышкой по голубому полю экрана.
Задание: Запишите рассуждения ученика при выполнении данного задания с использование правила деления разности на число
Выполните это задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Слайд 26Свойства деления (продолжение)
Деление произведения на число
Данное свойство можно сформулировать в виде правила:
Чтобы
Свойства деления (продолжение)
Деление произведения на число
Данное свойство можно сформулировать в виде правила:
Чтобы

Деление числа на произведение
Для любых целых неотрицательных чисел а, b и натурального числа с верно равенство: а :( b ⋅ с ) = (а : b) : с =(а : с) : b
(∀а ∈No, b, с ∈N) а :( b ⋅ с ) = (а : b) : с =(а : с) : b
Данное свойство можно сформулировать в виде правила:
Чтобы число разделить на произведение можно это число разделить сначала на один из множителей и полученный результат (частное) разделить на другой множитель.
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Сформулируйте это правило. Чтобы проверить себя щелкните мышкой по знаку вопроса. Для продолжения работы щелкните мышкой по голубому полю экрана.
Эти правила лежат в основе вычислительных приемов деления чисел, оканчивающихся нулями. Например:
480 : 6;
4800 : 12;
48000 : 16;
Развернутое решение этих примеров можно записать так:
480 : 6 =(48 ⋅ 10) : 6 = (48 : 6) ⋅ 10 = 8 ⋅ 10 = 80
4800 : 1200;
48000 : 1600.
4800 : 1200 =4800 : (12 ⋅ 100) = (4800 : 100) : 112 = 48 : 12 = 4
Задание: К каждой записи напишите соответствующее свойство.
Запишите развернутое решение остальных примеров.
Выполните это задание.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Слайд 27Для продолжения работы щелкните мышкой по управляющей кнопке.
Для просмотра иллюстраций к
Для продолжения работы щелкните мышкой по управляющей кнопке.
Для просмотра иллюстраций к
Для продолжения работы щелкните мышкой по голубому полю экрана.
Решите составленные задачи различными способами, записав решения выражением.
Запишите план решения задачи в каждом способе.
Запишите план анализа способов решения задачи, подводящий к выводу соответствующего правила деления.
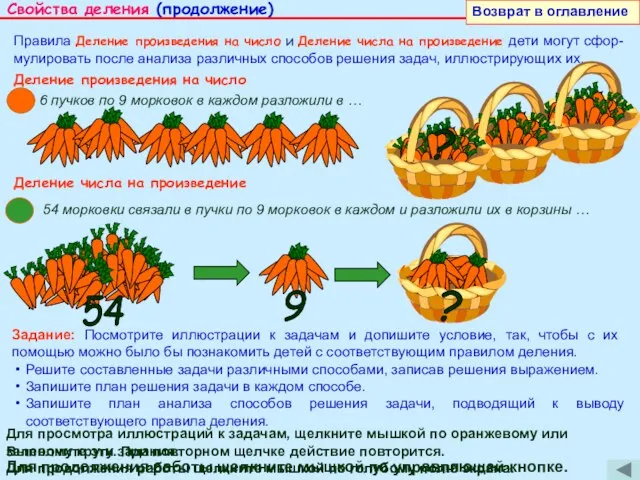
Правила Деление произведения на число и Деление числа на произведение дети могут сфор-мулировать после анализа различных способов решения задач, иллюстрирующих их.
Задание: Посмотрите иллюстрации к задачам и допишите условие, так, чтобы с их помощью можно было бы познакомить детей с соответствующим правилом деления.
6 пучков по 9 морковок в каждом разложили в …
Выполните эти задания.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Свойства деления (продолжение)
54 морковки связали в пучки по 9 морковок в каждом и разложили их в корзины …
Деление произведения на число
Деление числа на произведение
54
9
?
?
Слайд 28Изучение деления в начальном курсе математики
I этап. Ознакомление с делением. На этом
Изучение деления в начальном курсе математики
I этап. Ознакомление с делением. На этом

с конкретным смыслом деления;
с записью и чтением выражений с этим действием;
Результат деления на этом этапе находят, разбивая конкретные множества на
равночисленные подмножества.
Чтение выражения зависит от вида задачи, которую решает ребенок.
Например, выражение 15 : 5 может быть прочитано:
«пятнадцать разделить по 5» – , «пятнадцать разделить на 5» –
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
II этап. Изучение табличных случаев деления. На этом этапе дети:
знакомятся с названием чисел в делении (делимое, делитель, частное) и со способами чтения выражений. Например: 15 : 5 «Частное чисел 15 и 5»,
«Делимое – 15, делитель – 5, найти частное»;
знакомятся с правилами: нахождения неизвестного множителя, делимого, делителя;
изучают прием нахождения результата деления, как действия обратного умножению. Например: 28 : 7 «Чтобы получить двадцать восемь нужно семь умножить на четыре, следовательно 28 : 7 = 4».
составляют к каждой таблице умножения таблицы с соответствующими случаями деления.
знакомятся с особыми случаями деления:
деление на 1; деление нуля; невозможность деления на 0;
знакомятся с отношением «меньше в …». После этого знакомства добавляются варианты
чтения выражений. Например: 15 : 5 «Пятнадцать уменьшить в пять раз».
Выполните здание.
Для продолжения работы щелкните мышкой по управляющей кнопке.
деление на равные части
деление по содержанию
Запишите это в тетрадь, дописав вид задачи, соответствующий каждому способу чтения выражения. Проверьте себя, щелкнув мышкой по знаку вопроса.
При повторном щелчке подсказка исчезнет. Для продолжения работы щелкните мышкой по голубому полю экрана.
Задание: составьте таблицу умножения числа 7 и соответствующие ей таблицы деления.
Слайд 29Изучение действия деления в НКМ (продолжение)
Запишите это в тетрадь и щелкните мышкой
Изучение действия деления в НКМ (продолжение)
Запишите это в тетрадь и щелкните мышкой

IVэтап. Изучение алгоритмов письменного деления. На этом этапе дети:
знакомятся с алгоритмом деления на однозначное число, при этом
сначала рассматривают случаи, когда каждая цифра делимого делится на делитель. Например: 936 : 3; 468 : 2;
затем случаи, в которых при делении цифр числа получаются остатки, но количество цифр в делимом и частном совпадает, Например: 968 : 4; 496 : 2;
после этого рассматривают случаи, когда количество цифр в делимом и частном не совпадает. На этом этапе детей учат не только выделять неполное делимое, но и о пределять количество цифр в частном. Например: 136 : 4; 378 : 7;
и наконец рассматривают случаи, когда в частном получаются нули.
Например: 8136 : 4; 3780 : 7.
III этап. Изучение внетабличных случаев деления. На этом этапе дети:
учатся делить с остатком и проверять правильность подбора частного и остатка;
знакомятся с приемами деления, основанными на знании свойств (правил):
деление двузначного числа на однозначное; Например: 84 : 4; 96 : 6
деление круглых чисел. Например: 840 : 4; 96000 : 60
знакомятся с приемами деления двузначного числа на двузначное, основанными на связи деления с умножением, пользуясь правилом: Чтобы найти частное можно подобрать такое число, которое при умножении на делитель дает делимое.
Например: 48 : 16; 84 : 28; 76 : 19 и т. д
Задание: Решите все примеры, записанных выше.
Задание: запишите развернутое решение примеров, записанных выше, и рассуждения учеников при делении двузначного числа на двузначное. Чтобы посмотреть такое рассуж-дение, щелкните мышкой по знаку вопроса. При повторном щелчке подсказка исчезнет.
Сделайте записи в тетради и выполните задание.
Для продолжения работы щелкните мышкой по голубому полю экрана
48 : 16
Рассуждения ученика: «Попробуем число 2: 16 ⋅ 2 = 32 – мало; тогда попробуем 3: 16 ⋅ 3 = 48, значит 48 : 16 = 3»
Выполните здание.
Для продолжения работы щелкните мышкой по управляющей кнопке.
Слайд 30 IVэтап Изучение алгоритмов письменного деления. (продолжение)
знакомятся с алгоритмом деления на
IVэтап Изучение алгоритмов письменного деления. (продолжение)
знакомятся с алгоритмом деления на

сначала рассматривают случаи деления на круглое число с остатком, когда в частном получается одна цифра. Например: 638 : 90; 7350 : 800;
затем случаи деления на круглое число без остатка и в частном получается более одной цифры. Например: 3240 : 60; 5920 : 80;
после этого рассматривают случаи деления многозначного числа на многозначное, когда в частном получается сначала одна цифра, например: 432 : 72; 294 : 42; затем более одной цифры, например: 828 : 36; 4725 : 63;
наконец рассматривают случаи, когда в частном получаются нули. Сначала без остатка, например: 132192 : 324; 272640 : 284, а затем с остатком, например:
37971 : 73; 48574 : 712 .
Для продолжения работы вернитесь в оглавление.
Изучение действия деления в НКМ. (продолжение)
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Задание: Решите все примеры, записанные выше.
Если Вам нужно посмотреть пример рассуждений при использовании алгоритма деления, щелкните мышкой по знаку вопроса.
Выполните задание.
Для продолжения работы щелкните мышкой по голубому полю экрана
Чтобы ознакомиться с алгоритмом, щелкните мышкой по знаку вопроса.
Для продолжения работы щелкните мышкой по голубому полю экрана
Слайд 31Запишите это в тетрадь. Для ознакомления с каждым способом, щелкните мышкой по
Запишите это в тетрадь. Для ознакомления с каждым способом, щелкните мышкой по
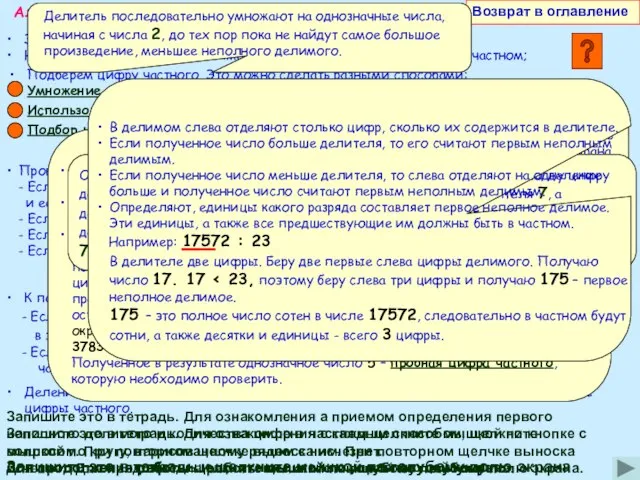
Проверяем полученную цифру. Для этого умножим на нее делитель.
- Если полученное произведение больше неполного делимого, то цифра подобрана неверно
и ее нужно уменьшить;
- Если полученное произведение меньше или равно неполному делимому, то найдем остаток.
- Если остаток больше или равен делителю, то цифру нужно увеличить;
- Если остаток меньше делителя, то цифра подобрана верно и ее можно записать в ответ.
Алгоритм деления многозначного числа на многозначное
Запишем числа уголком;
Найдем первое неполное делимое и определим количество цифр в частном;
Подберем цифру частного. Это можно сделать разными способами:
К полученному остатку справа припишем следующую цифру делимого.
Если полученное число меньше делителя, то единиц данного разряда в ответе не будет и
в этот разряд записывается 0;
Если полученное число больше делителя, то начинают подбирать следующую цифру
частного.
Деление заканчивается тогда, когда использованы все цифры делимого и найдены все цифры частного.
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Умножение делителя на однозначные числа; Способ округления;
Использование результатов предыдущих подборов;
Подбор цифры частного по последним цифрам делимого и делителя.
Делитель последовательно умножают на однозначные числа, начиная с числа 2, до тех пор пока не найдут самое большое произведение, меньшее неполного делимого.
Округлим делитель до круглого числа, содержащего только одну цифру
отличную от нуля. Например: 63 до числа 60; 631 до 600; 7836 до 8000 и т. д.
Представим полученное число в виде произведения цифры, отличной от нуля
и единицы с нулями. Например: 600 = 6 ⋅ 100.
Разделим неполное делимое на полученное произведение: сначала на единицу
с нулями (закроем у делимого справа столько цифр, сколько нулей в делителе), а потом полученное частное на цифру, отличную от нуля. Таким образом, подбор цифры сводится к делению двузначного числа на однозначное с остатком в пределах таблицы умножения При этом, нас интересует только частное, на остатки мы не обращаем внимания. Например: неполное делимое 3783 делим на округленный делитель 700 = 7 ⋅ 100
3783 : 100 = 37 (ост. не имеет значения) 37 : 7 = 5 (ост. не имеет значения)
Полученное в результате однозначное число 5 – пробная цифра частного,
которую необходимо проверить.
При подборе второй и последующих цифр частного, можно использовать результаты предыдущих подборов. Например: если ранее была подобрана цифра 5, а новое неполное делимое меньше (больше) предыдущих, значит в данном случае цифра частного будет меньше (больше) или равна 5.
Обычно так подбирают последнюю цифру частного, если уверены, что деление должно быть без остатка. Например: если последняя цифра делителя 7, а делимого 2, то по таблице умножения находят, число которое при умножении на 7 дает число, у которого в разряде единиц стоит 2. Это число 6:
7 ⋅ 6 = 4 2, значит можно проверять цифру 6.
Для продолжения работы щелкните мышкой по управляющей кнопке.
В делимом слева отделяют столько цифр, сколько их содержится в делителе.
Если полученное число больше делителя, то его считают первым неполным делимым.
Если полученное число меньше делителя, то слева отделяют на одну цифру больше и полученное число считают первым неполным делимым.
Определяют, единицы какого разряда составляет первое неполное делимое. Эти единицы, а также все предшествующие им должны быть в частном.
Например: 17572 : 23
В делителе две цифры. Беру две первые слева цифры делимого. Получаю число 17. 17 < 23, поэтому беру слева три цифры и получаю 175 – первое неполное делимое.
175 – это полное число сотен в числе 17572, следовательно в частном будут сотни, а также десятки и единицы - всего 3 цифры.
Запишите это в тетрадь. Для ознакомления а приемом определения первого неполного делимого и количества цифр в частном щелкните мышкой по кнопке с вопросом. При повторном щелчке выноска исчезнет.
Для продолжения работы щелкните мышкой по голубому полю экрана.
Слайд 32 Способом округления:
Округлим делитель 63 до числа 60.;
472 разделим на
Способом округления:
Округлим делитель 63 до числа 60.;
472 разделим на
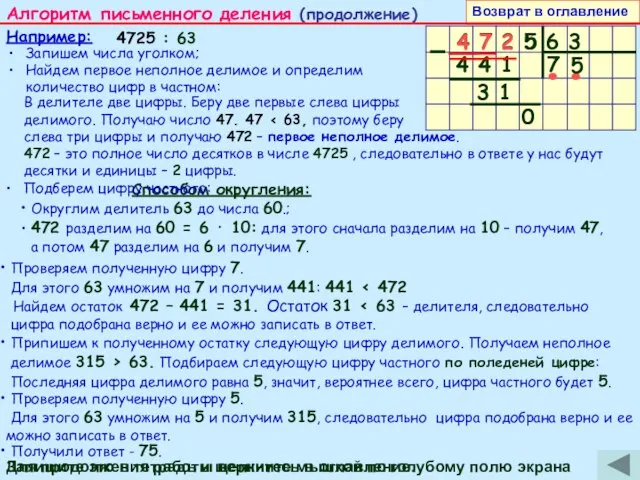
а потом 47 разделим на 6 и получим 7.
Алгоритм письменного деления (продолжение)
4 4 1
4 7 2 5 6 3
1
Запишем числа уголком;
Найдем первое неполное делимое и определим количество цифр в частном:
В делителе две цифры. Беру две первые слева цифры
делимого. Получаю число 47. 47 < 63, поэтому беру
слева три цифры и получаю 472 – первое неполное делимое.
472 – это полное число десятков в числе 4725 , следовательно в ответе у нас будут десятки и единицы – 2 цифры.
4 7 2
..
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Подберем цифру частного:
Например:
7
4725 : 63
Проверяем полученную цифру 7.
Для этого 63 умножим на 7 и получим 441: 441 < 472
Найдем остаток 472 – 441 = 31. Остаток 31 < 63 – делителя, следовательно
цифра подобрана верно и ее можно записать в ответ.
3 1
Припишем к полученному остатку следующую цифру делимого. Получаем неполное
делимое 315 > 63. Подбираем следующую цифру частного по поледеней цифре:
Последняя цифра делимого равна 5, значит, вероятнее всего, цифра частного будет 5.
5
Проверяем полученную цифру 5.
Для этого 63 умножим на 5 и получим 315, следовательно цифра подобрана верно и ее можно записать в ответ.
5
0
Получили ответ - 75.
Для продолжения работы вернитесь в оглавление.
Слайд 33 Способом округления:
Округлим делитель 63 до числа 60.;
472 разделим на
Способом округления:
Округлим делитель 63 до числа 60.;
472 разделим на
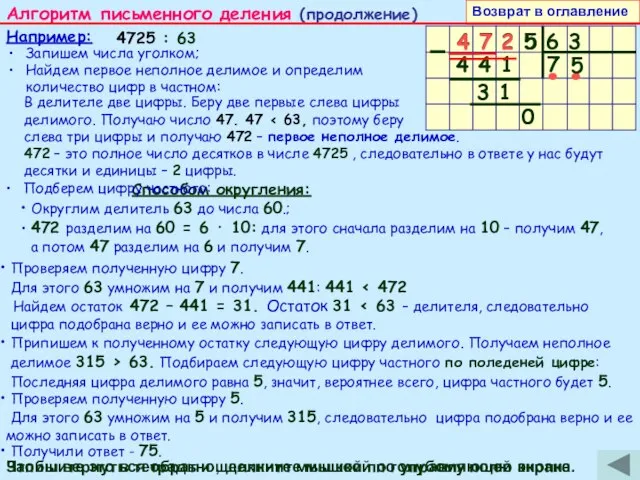
а потом 47 разделим на 6 и получим 7.
Алгоритм письменного деления (продолжение)
4 4 1
4 7 2 5 6 3
1
Запишем числа уголком;
Найдем первое неполное делимое и определим количество цифр в частном:
В делителе две цифры. Беру две первые слева цифры
делимого. Получаю число 47. 47 < 63, поэтому беру
слева три цифры и получаю 472 – первое неполное делимое.
472 – это полное число десятков в числе 4725 , следовательно в ответе у нас будут десятки и единицы – 2 цифры.
4 7 2
..
Запишите это в тетрадь и щелкните мышкой по голубому полю экрана
Подберем цифру частного:
Например:
7
4725 : 63
Проверяем полученную цифру 7.
Для этого 63 умножим на 7 и получим 441: 441 < 472
Найдем остаток 472 – 441 = 31. Остаток 31 < 63 – делителя, следовательно
цифра подобрана верно и ее можно записать в ответ.
3 1
Припишем к полученному остатку следующую цифру делимого. Получаем неполное
делимое 315 > 63. Подбираем следующую цифру частного по поледеней цифре:
Последняя цифра делимого равна 5, значит, вероятнее всего, цифра частного будет 5.
5
Проверяем полученную цифру 5.
Для этого 63 умножим на 5 и получим 315, следовательно цифра подобрана верно и ее можно записать в ответ.
5
0
Получили ответ - 75.
Чтобы вернуться обратно, щелкните мышкой по управляющей кнопке.
 Стипендия Правительства области
Стипендия Правительства области المالية االستدامة المالية
المالية االستدامة المالية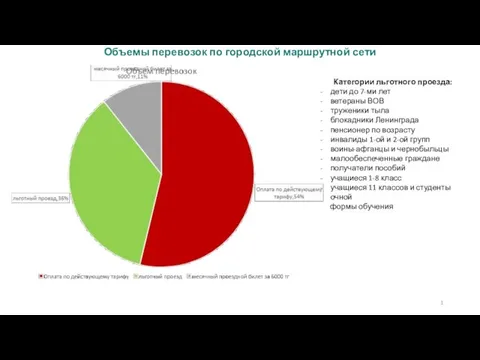 Объемы перевозок по городской маршрутной сети
Объемы перевозок по городской маршрутной сети День инвалида
День инвалида Презентация на тему Интернет и его возможности
Презентация на тему Интернет и его возможности Extenzionálne modely. Algebraická teória. Transformácie intervalov. Definícia funkcie Glob. (Téma 5)
Extenzionálne modely. Algebraická teória. Transformácie intervalov. Definícia funkcie Glob. (Téma 5) Культура Древней Греции
Культура Древней Греции Штриховая гладь
Штриховая гладь Профессия Повар-кондитер
Профессия Повар-кондитер Организационное стимулирование. Условия для внедрения мотивации персонала
Организационное стимулирование. Условия для внедрения мотивации персонала Что такое бенилюкс?
Что такое бенилюкс? Презентация на тему Здоровьесберегающие технологии на уроках в начальной школе. Окружающий мир 3 класс
Презентация на тему Здоровьесберегающие технологии на уроках в начальной школе. Окружающий мир 3 класс  FOOD SAFETY
FOOD SAFETY  Ассирия
Ассирия Презентация на тему Кометы и метеоры
Презентация на тему Кометы и метеоры Руководство Ernst&Young по составления бизнес-планов
Руководство Ernst&Young по составления бизнес-планов Куклы из махровых носков
Куклы из махровых носков Конституционные суды Приволжского Федерального округа
Конституционные суды Приволжского Федерального округа Японская каллиграфия - диалог культур Токио - Красноярск
Японская каллиграфия - диалог культур Токио - Красноярск «Пилот»: Маркетинг в компании
«Пилот»: Маркетинг в компании Устный журнал. В мире имён и названий
Устный журнал. В мире имён и названий Баскетбол. Тест по физической культуре
Баскетбол. Тест по физической культуре Материаловедение 5-6р
Материаловедение 5-6р Применение приборов серии IVS для решения задач вибродиагностики
Применение приборов серии IVS для решения задач вибродиагностики Композиционное решение для предприятий автомобилестроительной отрасли на основе системы MFG/PRO
Композиционное решение для предприятий автомобилестроительной отрасли на основе системы MFG/PRO Никола Тесла-повелитель молний
Никола Тесла-повелитель молний Проверка понимания озвученного текста
Проверка понимания озвученного текста Представление графической информации в компьютере
Представление графической информации в компьютере